Staff Selection Commission Mathematics - TIME AND WORK TYPE-III

Q.12

Some carpenters promised to do a job in 9 days but 5 of them were absent and remaining men did the job in 12 days. The original number of carpenters was

(1)24

(2)20

(3)16

(4)18

Ans .

(2)20

Explanation :
(2) Using Rule 1,
Let the original number of carpenters be x.
=>M₁D₁=M₂D₂
=>x * 9 = (x-5) * 12
=>9x = 12x-60
=>3x = 60 => x = 20

Q.13

2 men and 3 women together or 4 men together can complete a piece of work in 20 days.3 men and 3 women will complete the same work in :

(1)12 days

(2)16 days

(3)18 days

(4)19 days

Ans .

(2)16 days

Explanation :
(2) Using Rule 1,
=>2 men + 3 women = 4 men => 2 men = 3 women \ 3 men + 3 women = 5 men =>M₁D₁=M₂D₂
=> 4 * 20 = 5 *D₂
=>D₂=\( \frac{4*20}{5} \) =16 days.

Q.14

Working 8 hours a day, Anu can copy a book in 18 days. How many hours a day should she work so as to finish the work in 12 days ?

(1)12 hours

(2)10 hours

(3)11 hours

(4)13 hours

Ans .

(1)12 hours

Explanation :

Q.15

Some persons can do a piece of work in 12 days. Two times the number of such persons will do half of the work in

(1)9 days

(2)6 days

(3)5 days

(4)3 days

Ans .

(4)3 days

Explanation :

Q.16

If the work done by (x-1) men in(x+1) days is to the work done by (x+2) men in (x-1) days are in the ratio 9 : 10, then the value of x is equal to :

(1)5

(2)6

(3)7

(4)8

Ans .

(4)8

Explanation :

=> \( \frac{9}{10} \)=\( \frac{(x-1)(x+1)}{(x+2)(x-1))} \)=\( \frac{x+1}{x+2} \)
=>10x + 10 = 9x + 18
=> x = 18-10 = 8

Q.17

If 80 persons can finish a work within 16 days by working 6 hours a day, the number of hours a day, should 64 persons work to finish that very job within 15 days is :

(1)5 hrs.

(2)7 hrs.

(3)8 hrs.

(4)6 hrs.

Ans .

(3)8 hrs.

Explanation :
(3) Using Rule 1,
=>M₁D₁T₁=M₂D₂T₂
=>80*16*6 = 64*15*T₂
=>T₂ =\( \frac{80*16*6}{64*15} \)=8 hours.

Q.18

18 boys can do a piece of work in 24 days. In how many days can 27 boys do the same work ?

(1)16 days

(2)32 days

(3)23 days

(4)48 days

Ans .

(1)16 days

Explanation :
(1) Using Rule 1,
=>M₁D₁=M₂D₂
=>18 * 24 = 27 * D₂
D₂=\( \frac{18*24}{27} \)= 16 days.

Q.19

One man, 3 women and 4 boys can do a piece of work in 96 hours, 2 men and 8 boys can do it in 80 hours, 2 men and 3 women can do it in 120 hours.5 men and 12 boys can do it in

(1)39\( \frac{1}{11} \) hours

(2)42\( \frac{7}{11} \) hours

(3)43\( \frac{7}{11} \) hours

(4)44 hours

Ans .

(3)43\( \frac{7}{11} \) hours

Explanation :

Q.20

If x men can do a piece of work in x days, then the number of days in which y men can do the same work is

(1)xy days

(2)y²/x days

(3)x²/y days

(4)x²y days

Ans .

(3)x²/y days

Explanation :
(3) Using Rule 1,
=>M₁D₁= M₂D₂
=> x.x = y.D₂
=>D₂= x²/y days.

Q.21

30 men can repair a road in 18 days. They are joined by 6 more workers. Now the road can be repaired in

(1)14 days

(2)15 days

(3)16 days

(4)17 days

Ans .

(2)15 days

Explanation :
Using Rule 1,
=>M₁D₁= M₂D₂
=> 30 * 18 = 36 * D₂
=>D₂= \( \frac{30*18}{36} \) = 15 days.

Q.22

20 men or 24 women can complete a piece of work in 20 days. If 30 men and 12 women undertake to complete the work, the work will be completed in

(1)10 days

(2)12 days

(3)15 days

(4)16 days

Ans .

(1)10 days

Explanation :
1) 20 men = 24 women
=> 5 men = 6 women
=> 30 men + 12 women
= 40 men
=>M₁D₁= M₂D₂
=> 20 * 20 = 40 * D₂
D₂=\( \frac{20*20}{40} \)= 10 days.

Q.23

Either 8 men or 17 women can paint a house in 33 days. The number of days required to paint three such houses by 12 men and 24 women working at the same rate is :

(1)44 days

(2)43 days

(3)34 days

(4)66 days

Ans .

(3)34 days

Explanation :

Q.24

3 men and 7 women can do a job in 5 days, while 4 men and 6 women can do it in 4 days. The number of days required for a group of 10 women working together, at the same rate as before, to finish the same job is :

(1)30 days

(2)36 days

(3)40 days

(4)20 days

Ans .

(4)20 days

Explanation :
(4) 3 * 5 men + 7 * 5 women
= 4 * 4 men + 6 * 4 women
=> 16 men - 15 men = 35 women - 24 women
=>1 man = 11 women
=> 3 men + 7 women = 40 women
=>M₁D₁= M₂D₂
=> 40 * 5 = 10 * D₂
=>D₂ = 20 days.

Q.25

. A contractor undertook to finish a work in 92 days and employed 110 men. After 48 days, he found that he had already done \( \frac{3}{5} \)part of the work, the number of men he can withdraw so that the work may still be finished in time is :

(1)45

(2)40

(3)35

(4)30

Ans .

(4)30

Explanation :

Q.26

A man undertakes to do a certain work in 150 days. He employs 200 men. He finds that only a quarter of the work is done in 50 days. The number of additional men that should be appointed so that the whole work will be finished in time is :

(1)75

(2)100

(3)125

(4)50

Ans .

(2)100

Explanation :
(2) Using Rule 1,
200 men do \( \frac{1}{4} \) work in 50 days.

Q.27

A contractor undertook to finish a certain work in 124 days and employed 120 men. After 64 days, he found that he had already done \( \frac{2}{3} \) of the work. How many men can be discharged now so that the work may finish in time ?

(1)48

(2)56

(3)40

(4)50

Ans .

(2)56

Explanation :

Q.28

If 7 men working 7 hrs a day for each of 7 days produce 7 units of work, then the units of work produced by 5 men working 5 hrs a day for each of 5 days is

(1)\( \frac{25}{343} \)

(2)\( \frac{125}{49} \)

(3)\( \frac{49}{125} \)

(4)\( \frac{343}{25} \)

Ans .

(2)\( \frac{125}{49} \)

Explanation :

Q.29

Seventy-five men are employed to lay down a railway line in 3 months. Due to certain emergency conditions, the work was to be finished in 18 days. How many more men should be employed to complete the work in the desired time ?

(1)300

(2)325

(3)350

(4)375

Ans .

(1)300

Explanation :
(1) Using Rule 1,
=>M₁D₁ =M₂D₂
=>75 * 90 = M₂*18
=>M₂=\( \frac{75*90}{18} \)=375
=> Number of additional men = 375-75 = 300.

Q.30

. If 4 men or 8 women can do a piece of work in 15 days, in how many days can 6 men and 12 women do the same piece of work ?

(1)20 days

(2)45 days

(3)5 days

(4)30 days

Ans .

(3)5 days

Explanation :
(*) 4 men = 8 women
=> 1 man = 2 women
=> 6 men + 12 women
=> 12 women + 12 women = 24 women
=>M₁D₁ =M₂D₂
=> 8 * 15 = 24 * D₂
=>D₂ =\( \frac{8*15}{24} \)= 5days.

Q.31

24 men can do a piece of work in 17 days. How many men will be able to do it in 51 days ?

(1)8

(2)10

(3)12

(4)6

Ans .

(1)8

Explanation :
=>M₁D₁ =M₂D₂
=>24 * 17 = M₂*51
=>M₂ =\( \frac{24*17}{51} \) =8 men.

TYPE-VII

Q.1

Suman can do a work in 3 days.Sumati can do the same work in 2 days. Both of them finish the work together and get 150₹. What is the share of Suman ?

(1)₹30

(2)₹60

(3)₹70

(4)₹75

Ans .

(2)₹60

Explanation :
2) Ratio of Suman`s and Sumati`s 1 days work = \( \frac{1}{3} \):\( \frac{1}{2} \) =2:3
Sum of the ratios = 2 + 3 = 5
Suman`s share =\( \frac{2}{5} \)*150=₹60.

Q.2

The average wage of 500 workers was found to be ₹200. Later on, it was discovered that the wages of two workers were misread as 180 and 20 instead of 80 and 220. The correct average wage is :

(1)₹200.10

(2)₹200.20

(3)₹200.50

(4)₹201.00

Ans .

(2)₹200.20

Explanation :
(2) Total wages of 500 workers = 500 × 200 = 100000
Now, according to question,
Correct Average =\( \frac{100000-180-20+80+220}{500} \)
=> \( \frac{100100}{500} \) =₹200.20.

Q.3

A and B undertook to do a piece of work for ₹4500. A alone could do it in 8 days and B alone in 12 days. With the assistance of C they finished the work in 4 days. Then C’s share of the money is

(1)₹2250

(2)₹1500

(3)₹750

(4)₹375

Ans .

(3)₹750

Explanation :
(3) Using Rule 25,
C`s 1 days work =\( \frac{1}{4} \)-(\( \frac{1}{8} \)+\( \frac{1}{12} \))=\( \frac{1}{4} \)-(\( \frac{3+2}{24} \))
=>\( \frac{1}{4} \)-\( \frac{5}{24} \)=\( \frac{6-5}{24} \)=\( \frac{1}{24} \)
=>A : B : C =\( \frac{1}{8} \):\( \frac{1}{12} \):\( \frac{1}{24} \)=3:2:1
=> C's share =₹(\( \frac{1}{6} \)*4500)=₹750.

Q.4

If 6 persons working 8 hours a day earn ₹8400 per week, then 9 persons working 6 hours a day will earn per week

(1)₹8400

(2)₹16800

(3)₹9450

(4)₹16200

Ans .

(3)₹9450

Explanation :

Q.5

A alone can do a piece of work in 6 days and B alone in 8 days. A and B undertook to do it for ₹3200. With the help of C they completed the work in 3 days. How much is to be paid to C ?

(3)₹375

(2)₹400

(3)₹600

(4)₹800

Ans .

(2)₹400

Explanation :
(2) Using Rule 25,
A`s 1 days work =\( \frac{1}{6} \)
B`s 1 days work =\( \frac{1}{8} \) and (A + B + C)s 1 days work =\( \frac{1}{3} \)
C`s 1days work =\( \frac{1}{3} \)-\( \frac{1}{6} \)-\( \frac{1}{8} \)=\( \frac{8-4-3}{24} \)=\( \frac{1}{24} \)
Ratio of their one day’s work respectively=\( \frac{1}{6} \):\( \frac{1}{8} \):\( \frac{1}{24} \)=4:3:1
Sum of the ratios = 4 + 3 + 1 = 8
=> C`s share =\( \frac{1}{8} \)*3200=₹400.

Q.6

A and B can complete a piece of work in 15 days and 10 days respectively. They contracted to complete the work for ₹30,000. The share of A in the contracted money will be :

(1)₹ 18,000

(2)₹ 16,500

(3)₹12,500

(4)₹12,000

Ans .

(4)₹12,000

Explanation :
(4) A`s 1 days work =\( \frac{1}{15} \)
B`s 1 days work =\( \frac{1}{10} \)
Ratio =\( \frac{1}{15} \):\( \frac{1}{10} \)=2:3
Sum of the ratios = 2 + 3 = 5
A`s share =₹(\( \frac{2}{5} \)*300000) =₹12,000.

Q.7

A man and a boy received ₹800 as wages for 5 days for the work they did together. The man’s efficiency in the work was three times that of the boy. What are the daily wages of the boy ?

(1)₹76

(2)₹56

(3)₹44

(4)₹40

Ans .

(4)₹40

Explanation :
(4) Man : boy = 3 : 1
Boys share = \( \frac{1}{4} \)*800 = 200.
The daily wages of boy=₹(\( \frac{200}{5} \))=₹40.

Q.8

A daily-wage labourer was engaged for a certain number of days for ₹5,750; but being absent on some of those days he was paid only ₹5,000. What was his maximum possible daily wage?

(1)₹125

(2)₹250

(3)₹375

(4)₹500

Ans .

(2)₹250

Explanation :

Q.9

A, B and C completed a work costing ₹1,800. A worked for 6 days, B for 4 days and C for 9 days. If their daily wages are in the ratio of 5 : 6 : 4, how much amount will be received by A?

(1)₹800

(2)₹600

(3)₹900

(4)₹750

Ans .

(2)₹600

Explanation :
(2) Using Rule 25,
Ratio of wages of A, B and C respectively
= 5 * 6 : 6 * 4 : 4 * 9
= 30 : 24 : 36 = 5 : 4 : 6
Amount received by A =\( \frac{5}{5+4+6} \)*1800
=\( \frac{5}{15} \)*1800=₹600.

Q.10

A labourer was appointed by a contractor on the condition that he would be paid ₹75 for each day of his work but would be fined at the rate of ₹15 per day for his absence, apart from losing his wages, After 20 days, the contractor paid the labourer ₹1140. The number of days the labourer abstained from work was

(1)3

(2)5

(3)4

(4)2

Ans .

(3)4

Explanation :
(3) Total salary for 20 days= (75 × 20) = 1500
Actual salary received = 1140
Difference = (1500 – 1140) = 360
Money deducted for 1 day’s absencefrom work= (15 + 75) = 90
Number of days he was absent =\( \frac{360}{90} \)=4 days.

Q.11

Two men undertook to do a job for ₹1400. One of them can do it alone in 7 days, and the other in 8 days. With the assistance of a boy they together completed the work in 3 days. How much money will the boy get ?

(1)₹300

(2)₹325

(3)₹275

(4)₹250

Ans .

(3)₹275

Explanation :
(3) Using Rule 25,
First mans 1 days work =\( \frac{1}{7} \)
Second mans 1 days work =\( \frac{1}{8} \)
Let, Boys 1 days work =\( \frac{1}{x} \)
=>\( \frac{1}{7} \)+\( \frac{1}{8} \)+\( \frac{1}{x} \)=\( \frac{1}{3} \)
=>\( \frac{1}{x} \) = \( \frac{1}{3} \)-\( \frac{1}{7} \)-\( \frac{1}{8} \)
=>\( \frac{56-24-21}{168} \)=\( \frac{11}{168} \)
=> Ratio of their one days work=\( \frac{1}{7} \):\( \frac{1}{8} \):\( \frac{11}{168} \)=24:21:11
=>Sum of the ratios = 24 + 21 + 11= 56
=> Boy`s share in wages =\( \frac{11}{56} \)*1400 =₹275.

Q.12

If 5 men or 7 women can earn ₹5,250 per day, how much would 7 men and 13 women earn per day ?

(1)₹11,600

(2)₹11,700

(3)₹16,100

(4)₹17,100

Ans .

(4)₹17,100

Explanation :
(4) 5 men = 7 women
[Both earn same amount in 1 day]
7 men =\( \frac{7}{5} \)*7 =\( \frac{49}{5} \) women
7 men + 13 women
=>\( \frac{49}{5} \)+13 =\( \frac{114}{5} \) women
Now,7 women = 5250 => \( \frac{114}{5} \) women
=>\( \frac{5250}{7} \)*\( \frac{114}{5} \)=₹17,100.

Q.13

2 men and 1 woman together can complete a piece of work in 14 days, while 4 women and 2 men together can do it in 8 days. If a man gets ₹600 per day, how much should a woman get per day?

(1)₹400

(2)₹450

(3)₹480

(4)₹360

Ans .

(1)₹400

Explanation :
(1) According to the question,
(2 × 14) men + 14 women
= 16 men + 32 women
=>(28 – 16) men =(32–14) women
=> 12 men = 18 women
=> 2 men = 3 women
1 woman =\( \frac{2}{3} \)man
Amount received by 1 woman per day= \( \frac{2}{3} \)*600=₹400.

Q.14

Two men undertake a job for ₹960. They can complete it in 16 days and 24 days respectively. They work along with a third man and take 8 days to complete it. Then the share of the third man should be

(1)₹155

(2)₹165

(3)₹160

(4)₹150

Ans .

(3)₹160

Explanation :
(3) Using Rule 25,
Work done by the third person in 1 day=\( \frac{1}{8} \)-\( \frac{1}{16} \)-\( \frac{1}{24} \)=\( \frac{6-3-2}{48} \)=\( \frac{1}{48} \)
Ratio of their 1 day’s work=\( \frac{1}{16} \):\( \frac{1}{24} \):\( \frac{1}{48} \)=3:2:1
Share of the third person =\( \frac{1}{3+2+1} \)*960=\( \frac{960}{6} \)
=>₹160.

Q.15

If there is a reduction in the number of workers in a factory in the ratio 15 : 11 and an increment in their wages in the ratio 22 : 25, then the ratio by which the total wages of the workers should be decreased is

(1)6:5

(2)5:6

(3)3:7

(4)3:5

Ans .

(1)6:5

Explanation :
(1) Using Rule 25,
Required ratio = 15 * 22 : 11 * 25 = 6 : 5

Q.16

Stanie and Paul take a piece of work for ₹28,800. One alone could do it in 36 days, the other in 48 days. With the assistance of an expert, they finish it in 12 days. How much remuneration the expert should get ?

(1)₹10000

(2)₹18000

(3)₹16000

(4)₹12000

Ans .

(4)₹12000

Explanation :
(4) Expert`s 1 days work=\( \frac{1}{12} \)-\( \frac{1}{36} \)-\( \frac{1}{48} \)
=>\( \frac{12-4-3}{144} \)=\( \frac{5}{144} \)
Ratio of their respective work for 1 day =\( \frac{1}{36} \):\( \frac{1}{48} \):\( \frac{5}{144} \)=4:3:5
Experts share =\( \frac{5}{12} \)*28800=₹12000.

Q.17

A and B were assigned to do a job for an amount of ₹1,200. A alone can do it in 15 days, while B can do it in 12 days. With the help of C, they can finish in 5 days. The share of amount that C earns is

(1)₹300

(2)₹400

(3)₹500

(4)₹600

Ans .

(1)₹300

Explanation :
(1) Using Rule 25,
According to the question
\( \frac{1}{15} \) +\( \frac{1}{12} \) +\( \frac{1}{C} \) =\( \frac{1}{5} \)
Let C1s work in day be \( \frac{1}{C} \)
\( \frac{1}{C} \)=\( \frac{1}{5} \)-\( \frac{1}{15} \)-\( \frac{1}{12} \)=\( \frac{12-4-5}{60} \)=\( \frac{1}{20} \)
=>A:B:C=\( \frac{1}{15} \):\( \frac{1}{12} \):\( \frac{1}{20} \)=4:5:3
=> C`s share =\( \frac{3}{12} \)*1200 = ₹300.

Q.18

A sum of money is sufficient to pay A s wages for 21 days and B`s wages for 28 days. The same money is sufficient to pay the wages of both for :

(1)12\( \frac{1}{4} \)days

(2)14 days

(3)24\( \frac{1}{2} \) days

(4)12 days

Ans .

(4)12 days

Explanation :
(4) A`s 1 days work = \( \frac{1}{21} \)
B`s 1 days work = \( \frac{1}{28} \)
Total work done by both=\( \frac{1}{21} \)+\( \frac{1}{28} \)=\( \frac{4+3}{84} \)=\( \frac{1}{12} \)
Amount is sufficient to pay 12 days wages of both.

Q.19

A can do a piece of work in 12 days while B alone can do it in 15 days. With the help of C they can finish it in 5 days. If they are paid ₹960 for the whole work how much money A gets ?

(1)₹480

(2)₹240

(3)₹320

(4)₹400

Ans .

(4)₹400

Explanation :
(4) Rule 2 and Rule 25,
Work done by A and B in 5 days = 5(\( \frac{1}{12} \)+\( \frac{1}{15} \))
=5(\( \frac{5+4}{60} \))=\( \frac{9}{12} \)=\( \frac{3}{4} \)
Time taken by C in doing \( \frac{1}{4} \)work = 5 days
C will complete in 20 days.
Ratio of wages = \( \frac{1}{12} \):\( \frac{1}{15} \):\( \frac{1}{20} \)
=>5:4:3
Amount received by A= \( \frac{5}{12} \)*960 = ₹400

Q.20

A, B and C together earn ₹150 per day while A and C together earn ₹94 and B and C together earn ₹76. The daily earning of 'C' is

(1)₹56

(2)₹20

(3)₹34

(4)₹75

Ans .

(2)₹20

Explanation :
(2) The daily earning of 'C' = Daily earning of (A + C) and (B + C) - Daily earning of (A + B + C) = 94 + 76 - 150 = 20

Q.21

Three persons undertake to complete a piece of work for ₹1,200. The first person can complete the work in 8 days, second person in 12 days and third person in 16 days. They complete the work with the help of a fourth person in 3 days. What does the fourth person get?

(1)₹180

(2)₹280

(3)₹225

(4)₹250

Ans .

(3)₹225

Explanation :
(3) Rule 3 and Rule 25,
If the fourth person completes the work in x days, then
\( \frac{3}{8} \)+\( \frac{3}{12} \)+\( \frac{3}{16} \)+\( \frac{3}{x} \)=1
=>\( \frac{1}{x} \) = \( \frac{1}{3} \)-\( \frac{1}{8} \)-\( \frac{1}{12} \)-\( \frac{1}{16} \)
=>\( \frac{16-6-4-3}{48} \) =>\( \frac{1}{16} \)
x = 16
Ratio of wages =\( \frac{1}{8} \):\( \frac{1}{12} \):\( \frac{1}{16} \):\( \frac{1}{16} \)=6:4:3:3
Sum of ratios = 6 + 4 + 3+3 = 16
Fourth person`s share =\( \frac{3}{16} \)*1200=₹225.

Q.22

. A can do a piece of work in 16 days and B in 24 days. They take the help of C and three together finish the work in 6 days. If the total remuneration for the work is ₹400. The amount (in rupees) each will receive, in proportion, to do the work is

(1) A : 150, B : 100, C : 150

(2)A : 100, B : 150, C : 150

(3) A : 150, B : 150, C : 100

(4)A : 100, B : 150, C : 100

Ans .

(1) A : 150, B : 100, C : 150

Explanation :
(1) Rule 3 and Rule 25,
If C alone completes the work in x days, then
\( \frac{1}{16} \)+\( \frac{1}{24} \)+\( \frac{1}{x} \)=\( \frac{1}{6} \)
=> \( \frac{1}{x} \) = \( \frac{1}{6} \)-\( \frac{1}{16} \)-\( \frac{1}{24} \)
=>\( \frac{8-3-2}{48} \)=\( \frac{1}{16} \)
=>x = 16 days
Ratio of their remuneration =\( \frac{1}{16} \):\( \frac{1}{24} \):\( \frac{1}{16} \)= 3:2:2
A`s remuneration =\( \frac{3}{8} \)*400 = ₹150
B`s remuneration =\( \frac{2}{8} \)*400 =₹100
C`s remuneration =\( \frac{3}{8} \)*400 =₹150
=> A : 150, B : 100, C : 150

Q.23

A skilled, a half skilled and an unskilled labourer work for 7, 8 and 10 days respectively and they together get ₹369 for their work. If the ratio of their each day’s work is\( \frac{1}{3} \):\( \frac{1}{4} \):\( \frac{1}{6} \), then how much does the trained labourer get (in rupees) ? finish the piece of work.

(1)164

(2)102.50

(3)201.50

(4)143.50

Ans .

(4)143.50

Explanation :
(4) Using Rule 25,
Skilled : half skilled : unskilled =\( \frac{1}{3} \):\( \frac{1}{4} \):\( \frac{1}{6} \)
=>(\( \frac{1}{3} \)*12) :(\( \frac{1}{4} \)*12):(\( \frac{1}{6} \)*12)
= 4 : 3 : 2 Share of the trained labourer =\( \frac{28}{(7*4+8*3+2*10)} \) *369 =\( \frac{28}{28+24+20} \)*369
=>\( \frac{28}{72} \)*369 =143.50.

Q.24

A, B and C are employed to do a piece of work for ₹575. A and C are supposed to finish \( \frac{19}{23} \)of the work together. Amount shall be paid to B is

(1)₹210

(2)₹100

(3)₹200

(4)₹475

Ans .

(2)₹100

Explanation :
(2) Work done by B= 1-\( \frac{19}{23} \) = \( \frac{23-19}{23} \) = \( \frac{4}{23} \)
(A + C) : B = \( \frac{19}{23} \):\( \frac{4}{23} \) =19:4
Sum of ratios = 19 + 4 = 23
B`s share =\( \frac{4}{23} \)*575 =₹100

Q.25

If a man earns ₹2000 for his first 50 hours of work in a week and is then paid one and a half times his regular hourly rate for any additional hours, then the hours must he work to make ₹2300 in a week is

(1)6 hours

(2)4 hours

(3)7 hours

(4)5 hours

Ans .

(4)5 hours

Explanation :
Rate of earning of the man = 2000/50 = Rs. 40 per hour
Rate of earning for additional hours = 40 × 3/2 = Rs. 60 per hour
Let the man has to work for n additional hours.
Then, 2000 + n × 60 = 2300
⇒ n × 60 = 300
⇒ n = 5h.

Q.26

2 men and 1 woman can complete a piece of work in 14 days while 4 women and 2 men can do the same work in 8 days. If a man gets Rs. 180 per day, then a woman will get per day

(1)Rs.150

(2)Rs.140

(3)Rs.120

(4)Rs.160

Ans .

(3)Rs.120

Explanation :
(3) (2 men + 1 woman)s 14 days work = (4 women + 2 men)s 8 days work
=> 28 men + 14 women
=> 32 women + 16 men
=> (28 - 16) = 12 men
=> (32 - 14) = 18 women
=> 2 men = 3 women
1 woman = \( \frac{2}{3} \) man
=> Wages per day of 1 man = Rs. 180
=> Wages per day of 1 woman\( \frac{2}{3} \)*180 =Rs.120.

Q.27

The daily wages of A and B respectively are Rs.3.50 and Rs. 2.50. When A finishes a certain work, he gets a total wage of Rs. 63. When B does the same work, he gets a total wage of Rs.75. If both of them do it together what is the cost of the work ?

(1)Rs. 67.50

(2)Rs. 27.50

(3)Rs. 60.50

(4)Rs. 70.50

Ans .

(1)Rs. 67.50

Explanation :
(1) Time taken by A =\( \frac{63}{3.50} \)= 18 days
Time taken by B =\( \frac{75}{2.5} \) =30 days.
(A + B)s 1 days work =\( \frac{1}{18} \)+\( \frac{1}{30} \) = \( \frac{5+3}{90} \) =\( \frac{8}{90} \) = \( \frac{4}{45} \)
Required time =\( \frac{45}{4}\) days
Total wages =\( \frac{45}{4}\) * (3.50 + 2.50)
=>Rs(\( \frac{45}{4}\)*6) = )Rs. 67.5.

Q.28

A can do a work in 12 days while B can do it in 15 days. They undertake to complete it together for Rs. 450. what will be the share of A in this amount of money ?

(1) Rs.200

(2) Rs.240

(3) Rs.250

(4) Rs.300

Ans .

(3) Rs.250

Explanation :
(3) Ratio of A`s and B`s 1 days work =\( \frac{1}{12} \):\( \frac{1}{15} \) = 15:12 => 5:4
Sum of the terms of ratio = 5 + 4 = 9
A`s share = Rs.(\( \frac{5}{9} \)*450) = Rs.250.

Q.29

A, B and C can work together for Rs. 550. A and B together are to do \( \frac{7}{11} \)of the work. The share of C should be

(1)Rs. 200

(2)Rs. 300

(3)Rs. 400

(4)Rs. 450

Ans .

(1)Rs. 200

Explanation :
(1) Part of work done by C
=> 1- \( \frac{7}{11} \)-\( \frac{4}{11} \)
=> Total amount received = Rs. 550
=> C`s share = Rs(\( \frac{4}{11} \)*550) =Rs. 200.

Q.30

A and B undertake a piece of work for Rs. 250. A alone can do that work in 5 days and B alone can do that work in 15 days. With the help of C, they finish the work in 3 days. If every one gets paid in proportion to work done by them, the amount C will get is :

(1)Rs.50

(2)Rs.100

(3)Rs.150

(4)Rs.200

Ans .

(1)Rs.50

Explanation :
(1) Let C alone complete the work in x days.
According to the question,
\( \frac{1}{5} \)+\( \frac{1}{15} \)+\( \frac{1}{x} \)=\( \frac{1}{3} \)
=>\( \frac{1}{x} \) =\( \frac{1}{3} \)-\( \frac{1}{5} \)-\( \frac{1}{15} \)
=>\( \frac{5-3-1}{15} \) =>\( \frac{1}{15} \)
\ => x = 15 days = Time taken by C alone.
Ratio of the 1 day’s work of A, B and C =\( \frac{1}{5} \):\( \frac{1}{15} \):\( \frac{1}{15} \) => 3:1:1
Sum of the terms of ratio = 3 + 1 + 1 = 5
C’s share = Rs(\( \frac{1}{5} \)*250) => Rs.50

Q.31

A certain factory employed 600 men and 400 women and the average wage was ₹2.55 per day. If a women got 50 paise less than a man, the daily wages of a man and a woman were

(1) Man ₹2.75, Woman ₹2.25

(2) Man ₹5.30, Woman ₹2.50

(3)Man ₹2.50, Woman ₹2.00

(4) Man ₹3.25, Woman ₹2.75

Ans .

(1) Man ₹2.75, Woman ₹2.25

Explanation :
(1) Let daily wages of a man be Rs. x
Daily wages of a woman = Rs.(x-\( \frac{1}{2} \))
According to the question, 600x + 400(x-\( \frac{1}{2} \))
= 1000 × 2.55
=> 600x + 400x - 200 = 2550
=> 1000x = 2550 + 200 = 2750
=> x=\( \frac{2750}{1000} \) =Rs. 2.75
=> Daily wages of a woman
=>Rs. (2.75 – 0.5)
=>Rs. 2.25

TYPE-VIII

Q.1

A certain number of men can complete a job in 30 days. If there were 5 men more, it could be completed in 10 days less. How many men were in the beginning?

(1) 10

(2) 15

(3) 20

(4) 25

Ans .

(1) 10

Explanation :
(1) Let initially the number of men
be x.
=> According to question,
M₁D₁W₂ = M₂D₂W₁
x*30 = (x + 5)*(30 - 10)
x*30 = 20x + 100
30x - 20x = 100
10x = 100
x = 10

Q.2

If the expenditure of gas on burning 6 burners for 6 hours a day for 8 days is 450, then how many burners can be used for 10 days at 5 hours a day for Rs. 625 ?

(1) 12

(2) 16

(3) 4

(4) 8

Ans .

(4) 8

Explanation :
(4) Using Rule 1,

=> 450*10*5*x
= 625*8*6*6
=> x = \( \frac{625*8*6*6}{450*10*5} \) = 8

Q.3

A can do a piece of work in 60 days. He works for 15 days and then B alone finishes the remaining work in 30 days. The two together can finish the work in

(1) 24 days

(2) 25 days

(3) 30 days

(4) 32 days

Ans .

(1) 24 days

Explanation :
(1) Work done by A in 15 days
= \( \frac{1}{60} \)*15 = \( \frac{1}{4} \)
Remaining work = 1-\( \frac{1}{4} \) = \( \frac{3}{4} \)
Now, \( \frac{3}{4} \) work is done by B in 30
days
Whole work will be done by B in
\( \frac{30*4}{3} \) = 40 days
As 1 days work = \( \frac{1}{60} \) and Bs 1
days work = \( \frac{1}{40} \)
(A + B)s 1 days work
= \( \frac{1}{60} \)+\( \frac{1}{40} \) = \( \frac{2+3}{120} \) = \( \frac{5}{120} \) = \( \frac{1}{24} \)
Hence, both will finish the work in 24 days.

Q.4

A can do a piece of work in 60 days. He works for 15 days and then B alone finishes the remaining work in 30 days. The two together can finish the work in

(1) 24 days

(2) 25 days

(3) 30 days

(4) 32 days

Ans .

(2) 25 days

Explanation :
(2) As 1 days work
= (B +C)s 1 days work ...(i)
(A + B)s 1 days work = \( \frac{1}{10} \)
Cs 1 days work = \( \frac{1}{50} \)
(A + B + C)s 1 days work
= \( \frac{1}{10} \)+\( \frac{1}{50} \) = \( \frac{5+1}{50} \) = \( \frac{6}{50} \) = \( \frac{3}{25} \) ...(iii)
(A + A)s 1 days work = \( \frac{3}{25} \)
(By (i) & (iii)
As 1 days work = \( \frac{3}{50} \)
Bs 1 days work = \( \frac{1}{10} \)-\( \frac{3}{50} \)
= \( \frac{5-3}{50} \) = \( \frac{2}{50} \) = \( \frac{1}{25} \)
Hence, B alone will complete the
work in 25 days

Q.5

A man can do a piece of work in 5 days, but with the help of his son, he can do it in 3 days. In what time can the son do it alone ?

(1) 7 days

(2) 8 days

(3) 7\( \frac{1}{2} \) days

(4) 6\( \frac{1}{2} \) days

Ans .

(3) 7\( \frac{1}{2} \) days

Explanation :
(3) Using Rule 2,
Let the son take x days to do the
work.
\( \frac{1}{5} \)+\( \frac{1}{x} \) = \( \frac{1}{3} \)
=> \( \frac{x+5}{5x} \) = \( \frac{1}{2} \)
=> 3x + 15 = 5x
=> 2x = 15 => x = \( \frac{15}{2} \) = 7\( \frac{1}{2} \) days

Q.6

A certain number of men can do a work in 60 days. If there were eight more men, it could be completed in 10 days less. How many men were there in the beginning?

(1) 70

(2) 55

(3) 45

(4) 40

Ans .

(4) 40

Explanation :
(4) Let the number of men in the
beginning = x
Then, \( \frac{x+8}{x} \) = \( \frac{60}{50} \)
=> \( \frac{x+8}{x} \) = \( \frac{6}{5} \)
=> 6x = 5x + 40 => x = 40

Q.7

12 persons can do a piece of work in 4 days. How many persons are required to complete 8 times the work in half the time ?

(1) 192

(2) 190

(3) 180

(4) 144

Ans .

(1) 192

Explanation :
(1) 12 persons can complete a
work in 4 days.
=> 24 persons can complete the work in 2 days.
=> 24 persons can complete the 8 times work in 16 days
=> 24*8 persons = 192 persons can complete the 8 times work in 2 days.

Q.8

A work could be completed in 100 days by some workers. However, due to the absence of 10 workers, it was completed in 110 days. The original number of workers was :

(1) 100

(2) 110

(3) 55

(4) 50

Ans .

(2) 110

Explanation :
(2) Let the original number of
workers = x. Then,
x*100 = (x -10)*110
=> 10x = 11x - 110
=> x = 110

Q.9

A job can be completed by 12 men in 12 days. How many extra days will be needed to complete the job if 6 men leave after working for 6 days ?

(1) 3 days

(2) 6 days

(3) 12 days

(4) 24 days

Ans .

(3) 12 days

Explanation :
(3) Work done by 12 men in 6
days = \( \frac{1}{2} \)
Remaining work
= 1-\( \frac{1}{2} \) = \( \frac{1}{2} \)
6 men leave the work.
Time taken = \( \frac{12*12}{6*2} \) = 12 days

Q.10

60 men could complete a work in 250 days. They worked together for 200 days. After that the work had to be stopped for 10 days due to bad weather. How many more men should be engaged to complete the work in time ?

(1) 10

(2) 15

(3) 18

(4) 20

Ans .

(2) 15

Explanation :
(2) Using Rule 1,
60 men can complete a work in
250 days.
Work done by 60 men in 1 day
= \( \frac{1}{250} \)
=> Work done by 60 men in 200
days = \( \frac{200}{250} \) = \( \frac{4}{5} \)
Remaining work = 1-\( \frac{4}{5} \) = \( \frac{1}{5} \)
Work is stopped for 10 days.

Q.11

Working 5 hours a day, A can complete a work in 8 days and working 6 hours a day, B can complete the same work in 10 days. Working 8 hours a day, they can jointly complete the work in

(1) 3 days

(2) 4 days

(3) 4.5 days

(4) 5.4 days

Ans .

(1) 3 days

Explanation :
(1) Using Rule 2,
Working 5 hours a day, A can complete a work in 8 days.
i.e. A can complete the work in 40 hours.
Similarly, B will complete the same work in 60 hours.
(A + B)s 1 hours work
= \( \frac{1}{40} \)+\( \frac{1}{60} \) = \( \frac{3+2}{120} \)
= \( \frac{5}{120} \) = \( \frac{1}{24} \)
Hence, A and B together will complete the work in 24 hours.
They can complete the work in 3 days working 8 hours a day.

Q.12

If two persons, with equal abilities, can do two jobs in two days, then 100 persons with equal abilities can do 100 similar jobs in

(1) 100 days

(2) 10 days

(3) 5 days

(4) 2 days

Ans .

(4) 2 days

Explanation :
(4) According to the question,
2 persons with equal abilities can do 1 job in 1 day
Time taken by 1 man to complete 1 job = 2 days
=> Time taken by 100 persons in completing 100 jobs = 2 days

Q.13

Ganga and Saraswati, working separately can mow a field in 8 and 12 hours respectively. If they work in stretches of one hour alternately, Ganga beginning at 9 a.m., when will the moving be completed ?

(1) 6 p.m.

(2) 6.30 p.m.

(3) 5 p.m.

(4) 5.30 p.m.

Ans .

(2) 6.30 p.m.

Explanation :
(2) Part of the field mowed by
Ganga and Saraswati in first 2
hours
= \( \frac{1}{8} \)+\( \frac{1}{12} \) = \( \frac{3+2}{24} \) = \( \frac{5}{24} \)
Part of the field mowed in first
8 hours = \( \frac{5*4}{24} \) = \( \frac{20}{24} \) = \( \frac{5}{6} \)
Remaining work = 1 -\( \frac{5}{6} \) = \( \frac{1}{6} \)
Now, it is the turn of Ganga, part
of work done by Ganga in 1 hour = \( \frac{1}{8} \)
Remaining work = \( \frac{1}{6} \)-\( \frac{1}{8} \) = \( \frac{1}{24} \)
Now, time taken by Saraswati in
completing this part of work
= \( \frac{1}{24} \)*12 = \( \frac{1}{2} \) hour
Total time = 9*\( \frac{1}{2} \) hour
The mowing starts at 9 am.
Hence, the mowing will be completed
at 6.30 pm.

Q.14

A road of 5 km length will be constructed in 100 days. So 280 workers were employed. But after 80 days it was found that only 3\( \frac{1}{2} \) km road was completed. Now how many more people were needed to finish the work in the specified time ?

(1) 480

(2) 80

(3) 200

(4) 100

Ans .

(3) 200

Explanation :
(3) Using Rule 1,
Remaining work
= 5-\( \frac{7}{2} \) = \( \frac{3}{2} \)
M₁D₁W₂ = M₂D₂W₁
=> 280*80*\( \frac{3}{2} \) = M₂*20*\( \frac{7}{2} \)
=> M₂ = \( \frac{280*80*30}{20*7} \) = 480
Required number of additionalmen = 480 - 280 = 200

Q.15

A can do a work in 12 days. When he had worked for 3 days, B joined him. If they complete the work in 3 more days, in how many days can B alone finish the work?

(1) 6 days

(2) 12 days

(3) 4 days

(4) 8 days

Ans .

(1) 6 days

Explanation :
(1) Let B alone do the work in x
days.
6*\( \frac{1}{12} \) + 3*\( \frac{1}{x} \) = 1
=> \( \frac{1}{2} \)+\( \frac{3}{x} \) = 1
\( \frac{3}{x} \) = \( \frac{1}{2} \) => x = 6 days

Q.16

Working efficiencies of P and Q for completing a piece of work are in the ratio 3 : 4. The number of days to be taken by them to complete the work will be in the ratio

(1) 3:2

(2) 2:3

(3) 3:4

(4) 4:3

Ans .

(4) 4:3

Explanation :
(4) Using Rule 15,
Efficiency and time taken are inversely
proportional.
Required ratio = 4:3

Q.17

A contractor undertakes to make a road in 40 days and employs 25 men. After 24 days, he finds that only one-third of the road is made. How many extra men should he employ so that he is able to complete the work 4 days earlier?

(1) 100

(2) 60

(3) 75

(4) None of these

Ans .

(3) 75

Explanation :
(3) Scheduled time to complete the
work = 40 days
25 men in 24 days do \( \frac{1}{3} \) work
1 man in 1 day does \( \frac{1}{3*25*24} \) = \( \frac{1}{1800} \) work
Work remaining = 1-\( \frac{1}{3} \) = \( \frac{2}{3} \)
The work is to be completed 4
days before schedule i.e.,
in (40 - 4) = 36 days
No. of days left for \( \frac{2}{3} \)rd work
= 36 - 24 = 12 days
\( \frac{1}{1800} \) work is done in 1 day by
1 man.
\( \frac{2}{3} \)rd work will be done in 12 days
by
1800*\( \frac{2}{3} \)*\( \frac{1}{12} \) = 100 men
25 men are already working
Extra men to be employed
= 100 - 25 = 75

Q.18

Twenty women together can complete a work in 16 days. 16 men together can complete the same work in 15 days. The ratio of the working capacity of a man to that of a woman is :

(1) 3:4

(2) 4:3

(3) 5:3

(4) 4:5

Ans .

(2) 4:3

Explanation :
(2) 20*16 women
= 16*15 men
=> 4 women = 3 men
=> \( \frac{men}{women} \) = \( \frac{4}{3} \)
Hence, working capacity of man :
woman = 4:3

Q.19

A man and a woman working together can do a certain work in 18 days. Their skills in doing the work are in the ratio 3 : 2. How many days will the woman take to finish the work alone?

(1) 45 days

(2) 36 days

(3) 27 days

(4) 30 days

Ans .

(1) 45 days

Explanation :
(1) Man : Woman (efficiency)
= 3:2
i.e., Woman completes \( \frac{2}{5} \)
th work in 18 days.
Time taken by the woman to
complete the whole work = \( \frac{18*5}{2} \) = 45 days

Q.20

Two men can do a piece of work in x days. But y women can do that in 3 days. Then the ratio of the work done by 1 man and 1 woman is

(1) 3y:2x

(2) 2x:3y

(3) x:y

(4) 2y:3x

Ans .

(1) 3y:2x

Explanation :
(1) 1 mans 1 days work = \( \frac{1}{2x} \)
1 womans 1 days work = \( \frac{1}{3y} \)
Required ratio = \( \frac{1}{2x} \) \( \frac{1}{3y} \)
= 3y:2x

Q.21

A farmer can plough a field working 6 hours per day in 18 days. The worker has to work how many hours per day to finish the same work in 12 days ?

(1) 7 hrs

(2) 9 hrs

(3) 11 hrs

(4) 13 hrs

Ans .

(2) 9 hrs

Explanation :
(2) Using Rule 1,
D₁T₁ = DT₂
=> 18*6 = 12*T₂
=> T₂ = \( \frac{18*6}{12} \) = 9 hrs

Q.22

If 12 carpenters working 6 hours a day can make 460 chairs in 240 days, then the number of chairs made by 18 carpenters in 36 days each working 8 hours a day is

(1) 92

(2) 132

(3) 138

(4) 126

Ans .

(3) 138

Explanation :
(3) Using Rule 1,

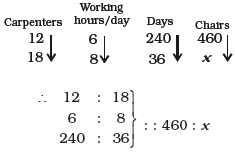=> 12*6*240*x = 18*8*36*460
=> x = \( \frac{18*8*36*460}{12*6*240} \) = 138

Q.23

8 workers can build a wall 18 m long, 2 m broad and 12 m high in 10 days, working 9 hours a day. Find how many workers will be able to build a wall 32 m long, 3 m broad and 9 m high in 8 days working 6 hours a day ?

(1) 16

(2) 20

(3) 30

(4) 10

Ans .

(3) 30

Explanation :
(3) Using Rule 1,

=> 18*2*12*6*8x = 32*3*9*9*10*8
=> x = \( \frac{32*3*9*9*10*8}{18*2*12*6*8} \) = 30 days

Q.24

P and Q together can do a job in 6 days. Q and R can finish the same job in \( \frac{60}{7} \) days. P started the work and worked for 3 days. Q and R continued for 6 days. Then the difference of days in which R and P can complete the job is

(1) 15

(2) 10

(3) 8

(4) 12

Ans .

(2) 10

Explanation :
(2) (P + Q)s 1 days work = \( \frac{1}{6} \)
(Q + R)s 1 days work = \( \frac{7}{60} \)
Let P alone do the work in x
days.
According to the question,
\( \frac{3}{x} \)+\( \frac{6*7}{60} \) = 1
=> \( \frac{3}{x} \) = 1-\( \frac{7}{10} \) = \( \frac{3}{10} \)
=> x = 10 days
Qs 1 days work = \( \frac{1}{6} \)-\( \frac{1}{10} \) = \( \frac{1}{15} \)
Rs 1 days work = \( \frac{7}{60} \)-\( \frac{1}{15} \) = \( \frac{1}{20} \)
Time taken by R = 20 days
Required answer = 20 - 10
= 10 days

Q.25

150 workers were engaged to finish a piece of work in a certain number of days. Four workers dropped on the second day, four more workers dropped on third day and so on. It takes 8 more days to finish the work now. Find the number of days in which the work was completed?

(1) 28

(2) 24

(3) 25

(4) 30

Ans .

(3) 25

Explanation :
(3) Let 150 workers complete the
work in x days.
150*x = 150 + 146 + .... to (x + 8) terms
On putting x = 17
LHS = 150*17 = 2550
RHS = 150 + 146 + .... to 25 terms
a = 150, d = - 4, n = 25
S = \( \frac{n}{2} \)*[2a+(n-1)d]
= \( \frac{25}{2} \)*[2*150 + 24*(-4)]
= \( \frac{25}{2} \)*(300-96) = 2550
Note : It is better to solve by options.

Q.26

Work done by (x + 4) men in (x + 5) days is equal to the work done by (x – 5) men in (x + 20) days. Then the value of x is

(1) 20

(2) 25

(3) 30

(4) 15

Ans .

(1) 20

Explanation :
(1) Using Rule 1,
According to the question,
M₁D₁ = M₂D₂
=>(x + 4)*(x + 5)
= (x - 5)*(x + 20)
=> x² + 5x + 4x + 20
= x² - 5x + 20x - 100
=> 9x + 20 = 15x - 100
=> 15x - 9x = 100 + 20
=> 6x = 120 => x = 20

Q.27

A group of workers can complete a piece of work in 50 days, when they are working individually. On the first day one person works, on the second day another person joins him, on the third day one more person joins them and this process continues till the work is completed. How many approximate days are needed to complete the work?

(1) 8 days

(2) 9 days

(3) 10 days

(4) 11 days

Ans .

(3) 10 days

Explanation :
(3) Let the work be finished in x
days.
\( \frac{x}{50} \)+\( \frac{x-1}{50} \)+\( \frac{x-2}{50} \)+ ... + \( \frac{1}{50} \) = 1
=> x + x - 1 + x - 2 + .... + 1 = 50
i.e., 10 + 9 + 8 + .... + 1
= 55
9 + 8 + .... + 1 = 45
Required time = 10 days

Q.28

20 men working 8 hours per day can complete a piece of work in 21 days. How many hours per day must 48 men work to complete the same job in 7 days?

(1) 12

(2) 20

(3) 10

(4) 15

Ans .

(3) 10

Explanation :
(3)

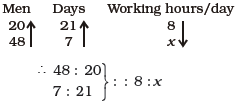=> 48*7*x = 20*21*8
=> x = \( \frac{20*21*8}{48*7} \) => x = 10

Q.29

The four walls and ceiling of a room of length 25 m, breadth 12 m and height 10 m are to be painted. Painter A can paint 200 m² in 5 days, Painter B can paint 250 m² in 2 days. If A and B work together, they will finish the job in

(1) 3y:2x 6 days

(2) 6\( \frac{10}{33} \) days

(3) 7\( \frac{10}{33} \) days

(4) 8 days

Ans .

(2) 6\( \frac{10}{33} \) days

Explanation :
(2) Area of the four walls and ceiling
of the room
= 2h (l + b) + lb
= 2*10 (25 + 12) + 25*12
= (20*37 + 300) sq. metre
= (740 + 300) sq. metre
= 1040 sq. metre
Area painted by A in 1 day
= \( \frac{250}{2} \) = 125 sq. metre
Area painted by both in1 day
= (125 + 40) sq. metre
= 165 sq. metre
Required time = \( \frac{1040}{165} \) = \( \frac{208}{33} \) = 6\( \frac{10}{33} \) days

Q.30

36 men together can build a wall 140 m long in 21 days. The number of men working at the same rate required to build the same wall in 14 days is

(1) 54

(2) 48

(3) 36

(4) 18

Ans .

(1) 54

Explanation :
(1) Here, the length of wall is
same in both cases.
M₁D₁ = M₂D₂
=> 36*21 = M₂*14
=> M₂ = \( \frac{36*21}{14} \) = 54 days

Q.31

A canteen requires 56 kgs of rice for seven days . The quantity of rice required for the months of April and May together is :

(1) 468 kg.

(2) 488 kg.

(3) 498 kg.

(4) 508 kg.

Ans .

(2) 488 kg.

Explanation :
(2) Number of days in April and
May = 30 + 31 = 61
Q Requirement of rice for 7 days = 56 kg.
Requirement of rice for 61 days
= \( \frac{56}{7} \)*61 = 488 kg.

Q.32

A school has 8 periods of 45 minutes each, everyday. How long will each period be if the school has to have 9 periods everyday, assuming the working hours to be the same?

(1) 40 minutes

(2) 35 minutes

(3) 30 minutes

(4) 45 minutes

Ans .

(1) 40 minutes

Explanation :
(1) Total working time of school
= (45*8) minutes
= 360 minutes
If 9 periods are held per day,
Working time of each period
\( \frac{360}{9} \) = 40 minutes

Q.33

If 7 spiders make 7 webs in 7 days, then 1 spider will make 1 web in how many days ?

(1) 1

(2) \( \frac{7}{2} \)

(3) 7

(4) 49

Ans .

(3) 7

Explanation :

Q.34

Sister can bake 50 cakes in 25 hours, Sister and Mummy together can bake 75 cakes in 15 hours. How many cakes Mummy can bake in 15 hours ?

(1) 25

(2) 45

(3) 20

(4) 10.

Ans .

(2) 45.

Explanation :

TEST YOURSELF

Q.1

A alone takes as much time as B and C together take to complete a piece of work. If A and B together take 10 days and B alone takes 50 days to complete it, in what time can A and C together do the work?

(1) 7\( \frac{1}{2} \) days

(2) 7\( \frac{1}{7} \)days

(3) 8\( \frac{1}{7} \) days

(4) 15\( \frac{1}{7} \)days

Ans .

(2) 7\( \frac{1}{7} \)days

Explanation :

Q.2

A can do a work in 12 days and B can do it in 16 days. A and B started the work jointly and A left 2 days before the work is finished. Find the number of days they took to finish the work.

(1) 6 days

(2) 7 days

(3) 9 days

(4) 8 days

Ans .

(4) 8 days

Explanation :

Q.3

A and B can do a piece of work in 10 days, B and C in 15 days and C and A in 20 days. C alone can do the work in :

(1)60 days

(2)120 days

(3)80 days

(4)30 days

Ans .

(2)120 days

Explanation :
(2) According to the question Work done by A and B together in one day =\( \frac{1}{10} \) part
Work done by B and C together

Q.4

12 men and 18 boys working 7\( \frac{1}{2} \)hours a day can do a work in 60 days. If one man works equal to 2 boys, then the number of boys required to help 21 men to do twice the work in 50 days working 9 hours a day will be :

(1)42

(2)44

(3)46

(4)(4) None of these

Ans .

(1)42

Explanation :
(1) Using Rule 1,

Q.5

Rita, Sita and Meeta are employed to do a piece of work for 625. Rita and Sita together are supposed to do \( \frac{17}{23} \) of the work. What should Meeta be paid?

(1)Rs.162.04

(2)RS.163.04

(3)Rs.161.04

(4)None of these

Ans .

(2)RS.163.04

Explanation :
(2) Using Rule 1,
Amount received by Meeta =\( \frac{6}{23} \)*625 = Rs. 163.04

Q.6

A contract is to be completedin 50 days and 105 men were set to work, each working 8 hours a day. After 25 days,\( \frac2{5} \) th of the work is finished.How many additional men be employed so that the work may be completed on time, each man now working 9 hours a day?

(1)35

(2)40

(3)45

(4)None of these

Ans .

(1)35

Explanation :

Q.7

If A alone can do a work in 12 days and B alone can do it in 8 days, Working together, in how many days will they complete it?

(1)4 \( \frac{4}{5} \)day

(2)4 day

(3)3\( \frac{4}{5} \)days

(4)6 days

Ans .

(1)4 \( \frac{4}{5} \)day

Explanation :
(1) A`s one days work =\( \frac{1}{12} \)
B`s one days work =\( \frac{1}{8} \)
(A + B)s one days work=\( \frac{1}{12} \)+\( \frac{1}{8} \) =\( \frac{2+3}{24} \) =\( \frac{5}{24} \)
Now,\( \frac{5}{24} \) work is done in 1day
1 work is done in = \( \frac{24}{5} \)days =4 \( \frac{4}{5} \) days.

Q.8

A can do \( \frac{1}{2} \) of a work in 9 days while B can do \( \frac{1}{3} \) of the same work in 6 days. How long would it take for A and B together to complete the work?

(1)8 days

(2)9 days

(3)10 days

(4)7 days

Ans .

(2)9 days

Explanation :

Q.9

A and B can do a work in 8 days. B alone can do it in 24 days. In how many days, A alone can do the same work?

(1)10 days

(2)9 days

(3)12 days

(4)14 days

Ans .

(3)12 days

Explanation :

Q.10

A and B can do a piece of work in 12 days, B and C in 15 days; C and A in 20 days. In how many days will they finish it working together? In what time can A do it separately?

(1)45 days

(2)20 days

(3)60 days

(4)30 days

Ans .

(4)30 days

Explanation :

Q.11

A, B and C can complete a work in 8 days. B alone can do it in 18 days and C alone can do it in 24 days. In how many days can A alone do the same work?

(1)36 days

(2)24 days

(3)38 days

(4)30 days

Ans .

(1)36 days

Explanation :

Q.12

A can do a piece of work in 40 days. He works on it for 5 days and then B completes it in 21 days. How long will A and B together take to complete the work?

(1)10 days

(2)15 days

(3)20 days

(4)25 days

Ans .

(2)15 days

Explanation :

Q.13

Ram can do a piece of work in 20 days and Shyam in 30 days. They work together for 10 days. After that Shyam leaves and rest of the work is completed by Ram alone. How long does it take Ram to finish the remaining work?

(1)3 days

(2)2\( \frac{1}{3} \) days

(3)3\( \frac{1}{3} \) days

(4)4\( \frac{1}{3} \) days

Ans .

(3)3\( \frac{1}{3} \) days

Explanation :

Q.14

A and B can complete a piece of work in 45 and 40 days respectively. Both started to work together, but after some days A left and B alone completed the rest work in 23 days. For how many days did A work?

(1)12 days

(2)10 days

(3)8 days

(4)9 days

Ans .

(4)9 days

Explanation :

Q.15

. A and B together can finish a work in 15 days. A and C take 2 days more to complete the same work than that of B and C. A, B and C together complete the work in 8 days. In how many days will A finish it separately?

(1)40 days

(2)24 days

(3)17\( \frac{1}{7} \) days

(4)20 days

Ans .

(1)40 days

Explanation :

Q.16

A and B together can do a piece of work in 30 days, B and C together can do it in 20 days. A starts the work and works on it for 5 days, then B takes it up and works for 15 days. Finally C finishes the work in 18 days. In how many days can C do the work when doing it separately?

(1)40 days

(2)24 days

(3)120 days

(4)60 days

Ans .

(2)24 days

Explanation :

Q.17

A and B can do a piece of work in 30 days while B and C can do the same work in 24 days and C and A in 20 days. They all work for 10 days when B and C leave. How many days more will A take to complete the work?

(1)16 days

(2)15 days

(3)18 days

(4)20 days

Ans .

(3)18 days

Explanation :

Q.18

A, B and C can complete a work separately in 24, 36 and 48 days respectively. They started together but C left after 4 days of start and A left 3 days before the completion of work. In how many days will the work be completed?

(1)20 days

(2)18 days

(3)16 days

(4)15 days

Ans .

(4)15 days

Explanation :

Q.19

. A can complete a work in 24 days, B in 32 days and C in 64 days. They start together. A works for 6 days and leaves and B leaves 6 days before the work is finished. In how many days was the work finished?

(1)20 days

(2)21 days

(3)22 days

(4)25 days

Ans .

(1)20 days

Explanation :

Q.20

A can complete a work in 10 days, B can complete the same work in 20 days and C in 40 days. A starts working on the first day, B works for second day and C works for third day. Again A works for fourth day and B for fifth day and so on. If they continued working in the same way, in how many days will the work be completed?

(1)15 days

(2)16.5 days

(3)15.5 days

(4)17 days

Ans .

(2)16.5 days

Explanation :

Q.21

A can do a piece of work in 120 days and B can do it in 150 days. They work together for 20 days. Then B leaves and A alone continues the work. 12 days after that C joins A and the work is completed in 48 days more. In how many days can C do it if he works alone?

(1)230 days

(2)225 days

(3)240 days

(4)220 days

Ans .

(3)240 days

Explanation :

upscfever.com

Journey of a Thousand Miles begins with One Click!!!

Staff Selection Commission Mathematics - TIME AND WORK TYPE-III

TYPE-VII

TYPE-VIII

TEST YOURSELF

UPSCFEVER - POPULAR PAGES

Join The Movement

Discussions and Comments