PROBABILITY - Aptitude

Chapter 17: PROBABILITY

Introduction

Probability means the chance of the occurrence of an event. In layman terms, we can say that it is the likelihood that something—that is defined as the event—will or will not occur.

The factors underlying an event often affect the probability of that event’s occurrence.

For instance, if we estimate the probability of India winning the 2015 World Cup as 0.14 based on certain expectations of outcomes, then this probability will definitely improve if we know that Sachin Tendulkar will score 800 runs in that particular World Cup.

As we now move towards the mathematical aspects of the chapter, one underlying factor that recurs in every question of probability is that whenever one is asked the question, what is the probability? the immediate question that arises/should arise in one’s mind is the probability of what?

The answer to this question is the probability of the EVENT.

The EVENT is the cornerstone or the bottomline of probability. Hence, the first objective while trying to solve any question in probability is to define the event.

The event whose probability is to be found out is described in the question and the task of the student in trying to solve the problem is to define it.

In general, the student can either define the event narrowly or broadly.

Narrow definitions of events are the building blocks of any probability problem and whenever there is a doubt about a problem, the student is advised to get into the narrowest form of the event definition.

The Use of the Conjunction AND

If A AND B have to occur, and if the probability of their occurrence are P(A) and P(B) respectively, then the probability that A AND B occur is got by connecting P(A) AND P(B). Replacing the AND by multiplication sign we get the required probability as:

P(A) × P(B)

Q. If we have the probability of A hitting a target as 1/3 and that of B hitting the target as 1/2, then the probability that both hit the target if one shot is taken by both of them is got by

A hits the target AND B hits the target

P(A) × P(B) = 1/3 × 1/2 = 1/6

(Note that since we use the conjunction AND in the definition of the event here, we multiply the individual probabilities that are connected through the conjunction AND.)

The Use of the Conjunction OR

If A OR B have to occur, and if the probability of their occurrence are P(A) and P(B) respectively, then the probability that A OR B occur is got by connecting P(A) OR P(B).

Replacing the OR by addition sign, we get the required probability as P(A) + P(B)

Example : If we have the probability of A winning a race as 1/3 and that of B winning the race as 1/2, then the probability that either A or B win a race is got by

A wins OR B wins. so P(A) + P(B) = 1/3 + 1/2 = 5/6 (Note that since we use the conjunction OR in the definition of the event here, we add the individual probabilities that are connected through the conjunction OR.)

Combination of AND and OR

If two dice are thrown, what is the chance that the sum of the numbers is not less than 10.

The sum of the numbers is not less than 10 if it is either 10 OR 11 OR 12. Which can be done by

(6 AND 4) OR (4 AND 6) OR (5 AND 5) OR (6 AND 5) OR (5 AND 6) OR (6 AND 6) that is, 1/6 × 1/6 + 1/6 × 1/6 + 1/6 × 1/6 + 1/6 × 1/6 + 1/6 × 1/6 + 1/6 × 1/6 = 6/36 = 1/6

The bottomline is that no matter how complicated the problem on probability is, it can be broken up into its narrower parts, which can be connected by ANDs and ORs to get the event definition. Once the event is defined, the probability of each narrow event within the broad event is calculated and all the narrow events are connected by Multiplication (for AND) or by Addition (for OR) to get the final solution

BASIC FACTS ABOUT PROBABILITY

For every event that can be defined, there is a corresponding non-event, which is the opposite of the event. The relationship between the event and the non-event is that they are mutually exclusive, that is, if the event occurs then the non-event does not occur and vice versa.

The event is denoted by E; the number of ways in which the event can occur is defined as n(E) and the probability of the occurrence of the event is P(E).

The non-event is denoted by E'; the number of ways in which the non-event can occur is defined as n(E') while the probability of the occurrence of the event is P(E').

The following relationships hold true with respect to the event and the non-event n(E) + n(E') = sample space representing all the possible events that can occur related to the activity.

P(E) + P(E') = 1

This means that if the event does not occur, then the non-event occurs. Æ P(E) = 1 – P(E')

This is often very useful for the calculation of probabilities of events where it is easier to describe and count the non-event rather than the event.

The Concept of Odds For and Odds Against

Sometimes, probability is also viewed in terms of odds for and odds against an event

Odds in favour of an event E is defined as P(E) / P(E')

Odds against an event is defined as: P(E') / P(E)

Expectation: The expectation of an individual is defined as Probability of winning × Reward of winning

Q. A man holds 20 out of the 500 tickets to a lottery. If the reward for the winning ticket is ` 1000, find the expectation of the man.

Expectation = Probability of winning × Reward of winning = \( \frac{20}{500} * 1000 = 40 \)

The probability of an event is defined as

= \( \frac{\text{Number of ways in which event occurs}}{\text{Total number of outcomes possible}}\)

This means that the probability of any event can be got by counting the numerator and the denominator independently. Hence, from this approach, the concentration shifts to counting the numerator and the denominator. Thus for the example used above, the probability of a number > 2 appearing on a dice is: = \( \frac{\text{Number of ways in which event occurs}}{\text{Total number of outcomes possible}}\) = 4/6

Sample Space: It is a set of all possible outcomes of an experiment i.e. a sample space for an experiment of rolling a die is {1,2,3,4,5,6} and tossing a coin = {H,T}.

Event: It is a subset of a sample space i.e. Heads or Tails.

Mutually exclusive events: If two or more events have nothing in common then they are mutually exclusive.

The sum of probabilities is 1 i.e The probability of getting heads on a coin toss is 1/2 and getting tails on a coin toss is 1/2 so total probability of all events in a sample space is 1.

Conditional probability: P ( B / A ) is the probability of an event B occurring given that event A has already occurred.

P ( B / A ) = P (A ∩ B) / P (A)

P (A ∩ B) = P (A) * P ( B / A )

Independent events:
If the happening of an event is not influenced by another event then we say A and B are mutually independent. Mutually exclusive events in general are not independent.
P (A ∩ B) = P (A) * P ( B )

P (atleast one) = 1 - P (none)

In a throw of two dice, find the probability of getting one prime and one composite number

1/6

11/51

1/2

1/3

Explanation :

The probability of getting a prime number when a dices is thrown is 3/6 = 1/2. (This occurs
when we get 2, 3 or 5 out of a possibility of getting 1, 2, 3, 4, 5 or 6.)
Similarly, in a throw of a dice, there are only 2 possibilities of getting composite numbers viz : 4 or 6 and
this gives a probability of 1/3 for getting a composite number.
Now, let us look at defining the event. The event is—getting one prime and one composite number.
This can be got as:
The first number is prime and the second is composite OR the first number is composite and the second is
prime.
= (1/2) × (1/3) + (1/3) × (1/2) = 1/3

Find the probability that a leap year chosen at random will have 53 Sunday

2/7

12/17

2/17

1/4

Explanation :

A leap year has 366 days. 52 complete weeks will have 364 days. The 365th day can be a
Sunday (Probability = 1/7) OR the 366th day can be a Sunday (Probability = 1/7). Answer = 1/7 + 1/7 =
2/7.
Alternatively, you can think of this as: The favourable events will occur when we have Saturday and
Sunday or Sunday and Monday as the 365th and 366th days respectively. (i.e. 2 possibilities of the event
occurring). Besides, the total number of ways that can happen are Sunday and Monday OR Monday and
Tuesday … OR Friday and Saturday OR Saturday and Sunday.

There are two bags containing white and black balls. In the first bag, there are 8 white and 6 black balls and in the second bag, there are 4 white and 7 black balls. One ball is drawn at random from any of these two bags. Find the probability of this ball being black

41/77

2/3

21/77

36/77

Explanation :

The event definition here is: 1st bag and black ball OR 2nd Bag and Black Ball. The chances of
picking up either the 1st OR the 2nd Bag are 1/2 each.
Besides, the chance of picking up a black ball from the first bag is 6/14 and the chance of picking up a
black ball from the second bag is 7/11.
Thus, using these values and the ANDs and ORs we get:
(1/2) × (6/14) + (1/2) × (7/11) = (3/14) + (7/22) = (66 + 98)/(308) = 164/308 = 41/77

The letters of the word LUCKNOW are arranged among themselves. Find the probability of always having NOW in the word

1/42

13/42

12/42

11/42

Explanation :

The required probability will be given by the equation
= No. of words having NOW/Total no. of words
= 5!/7! = 1/42

A person has 3 children with at least one boy. Find the probability of having at least 2 boys among the children.

3/4

3/114

13/14

3/14

Explanation :

The event is occurring under the following situations:
(a) Second is a boy and third is a girl OR
(b) Second is a girl and third is a boy OR
(c) Second is a boy and third is a boy
This will be represented by: (1/2) × (1/2) + (1/2) × (1/2) + (1/2) × (1/2) = 3/4

Out of 13 applicants for a job, there are 5 women and 8 men. Two persons are to be selected for the job. The probability that at least one of the selected persons will be a woman is

5/9

25/139

2/39

25/39

Explanation :

The required probability will be given by
First is a woman and Second is a man OR
First is a man and Second is a woman OR
First is a woman and Second is a woman
i.e. (5/13) × (8/12) + (8/13) × (5/12) + (5/13) × (4/12) = 100/156 = 25/39
Alternatively, we can define the non-event as: There are two men and no women. Then, probability of the
non-event is
(8/13) × (7/12) = 56/156
Hence, P(E) = (1– 56/156) = 100/156 = 25/39

The probability that A can solve the problem is 2/3 and B can solve it is 3/4. If both of them attempt the problem, then what is the probability that the problem gets solved.

11/12

7/12

4/12

1/12

Explanation :

 The event is defined as:
A solves the problem AND B does not solve the problem
OR
A doesn’t solve the problem AND B solves the problem
OR
A solves the problem AND B solves the problem.
Numerically, this is equivalent to:
(2/3) × (1/4) + (1/3) × (3/4) + (2/3) × (3/4)
= (2/12) + (3/12) + (6/12) = 11/12

Six positive numbers are taken at random and are multiplied together. Then what is the probability that the product ends in an odd digit other than 5.

(0.4)⁴

(0.4)³

(0.4)²

(0.4)⁶

Explanation :

The event will occurs when all the numbers selected are ending in 1, 3, 7 or 9.
If we take numbers between 1 to 10 (both inclusive), we will have a positive occurrence if each of the six
numbers selected are either 1, 3, 7 or 9.
The probability of any number selected being either of these 4 is 4/10 (4 positive events out of 10
possibilities)
[Note: If we try to take numbers between 1 to 20, we will have a probability of 8/20 = 4/10. Hence, we
can extrapolate up to infinity and say that the probability of any number selected ending in 1, 3, 7 or 9 so
as to fulfill the requirement is 4/10.]
Hence, answer = (0.4)⁶

The probability that Arjit will solve a problem is 1/5. What is the probability that he solves at least one problem out of ten problems?

(4/5)¹⁰

1-(4/5)⁸

1-(4/5)⁷

1-(4/5)¹⁰

Explanation :

The non-event is defined as:
He solves no problems i.e. he doesn’t solve the first problem and he doesn’t solve the second problem …
and he doesn’t solve the tenth problem.
Probability of non-event = (4/5)¹⁰
Hence, probability of the event is 1-(4/5)¹⁰

A carton contains 25 bulbs, 8 of which are defective. What is the probability that if a sample of 4 bulbs is chosen, exactly 2 of them will be defective?

(4C2) × (8/25) × (7/24) × (17/23) × (16/22)

(4C2) × (8/25) × (7/24) × (17/23)

(4C2) × (8/25) × (17/23) × (16/22)

(4C2) × (7/24) × (17/23) × (16/22)

Explanation :

The probability that exactly two balls are defective and exactly two are not defective will be
given by (4C2) × (8/25) × (7/24) × (17/23) × (16/22)

Out of 40 consecutive integers, two are chosen at random. Find the probability that their sum is odd.

20/39

2/9

20/9

2/39

Explanation :

Forty consecutive integers will have 20 odd and 20 even integers. The sum of 2 chosen integers
will be odd, only if
(a) First is even and Second is odd OR
(b) First is odd and Second is even
Mathematically, the probability will be given by:
P(First is even) × P(Second is odd) + P(First is odd) × P(second is even)
= (20/40) × (20/39) + (20/40) × (20/39)
= (2 × 20
2
/40 × 39) = 20/39

An integer is chosen at random from the first 100 integers. What is the probability that this number will not be divisible by 5 or 8?

17/100

7/100

7/10

47/100

Explanation :

For a number from 1 to 100 not be divisible by 5 or 8, we need to remove all the numbers that
are divisible by 5 or 8.
Thus, we remove 5, 8, 10, 15, 16, 20, 24, 25, 30, 32, 35, 40, 45, 48, 50, 55, 56, 60, 64, 65, 70, 72, 75, 80,
85, 88, 90, 95, 96, and 100.
i.e. 30 numbers from the 100 are removed.
Hence, answer is 70/100 = 7/10 (required probability)
Alternatively, we could have counted the numbers as number of numbers divisible by 5 + number of
numbers divisible by 8 – number of numbers divisible by both 5 or 8.
= 20 + 12 – 2 = 30

From a bag containing 8 green and 5 red balls, three are drawn one after the other. Find the probability of all three balls being green if (a) the balls drawn are replaced before the next ball is picked

3¹³/13¹³

7¹³/13¹³

9¹³/13¹³

8¹³/13¹³

Explanation :

When the balls drawn are replaced, we can see that the number of balls available for drawing out
will be the same for every draw. This means that the probability of a green ball appearing in the
first draw and a green ball appearing in the second draw as well as one appearing in the third
draw are equal to each other.
Hence answer to the question above will be:
Required probability =  \( \frac{8}{13} * \frac{8}{13} * \frac{8}{13} = \frac{8^3}{13^3}\)

From a bag containing 8 green and 5 red balls, three are drawn one after the other. Find the probability of all three balls being green if the balls drawn are not replaced.

\( \frac{8}{13} * \frac{7}{12} * \frac{6}{11}\)

\( \frac{9}{13} * \frac{7}{12} * \frac{6}{11}\)

\( \frac{2}{13} * \frac{7}{12} * \frac{6}{11}\)

\( \frac{5}{13} * \frac{7}{12} * \frac{6}{11}\)

Explanation :

When the balls are not replaced, the probability of drawing any color of ball for every fresh draw
changes. Hence, the answer here will be:
Required probability = \( \frac{8}{13} * \frac{7}{12} * \frac{6}{11}\)

In throwing a fair dice, what is the probability of getting the number ‘3’?

1/3

1/6

1/9

1/12

Explanation :

Out of a total of 6 occurrences, 3 is one possibility = 1/6.

What is the chance of throwing a number greater than 4 with an ordinary dice whose faces are numbered from 1 to 6?

1/3

1/6

1/9

1/12

Explanation :

5 or 6 out of a sample space of
1, 2, 3, 4, 5 or 6 = 2/6 = 1/3

Find the chance of throwing at least one ace in a simple throw with two dice.

1/12

1/3

1/6

11/36

Explanation :

Event definition is:
(1 and 1) or (1 and 2) or (1 and 3) or (1 and 4) or (1 and 5) or (1 and 6) or (2 and 1) or (3 and 1)
or (4 and 1) or (5 and 1) or (6 and 1)
Total 11 out of 36 possibilities = 11/36

Q5: A bag contains 6 white balls and 4 black balls. Probability that they are of different colors.

6C1*4C1/10C2

6/10

4/10

2/3

Find the chance of drawing 2 blue balls in succession from a bag containing 5 red and 7 blue balls, if the balls are not being replaced

1/22

6/23

7/22

14/22

Explanation :

Event definition: First is blue and second is blue = 7/12 × 6/11 = 7/22.

From a pack of 52 cards, two are drawn at random. Find the chance that one is a knave and the other a queen.

8/663

17/663

13/663

11/663

Explanation :

Knave and queen or Queen and Knave so
4/52 × 4/51 + 4/52 × 4/51 = 8/663

If a card is picked up at random from a pack of 52 cards. Find the probability that it is (i) a spade.

1/6

1/13

4/16

1/4

Explanation :
```
13/52 = 1/4
```

If a card is picked up at random from a pack of 52 cards. Find the probability that it is a king or queen.

2/13

7/13

5/13

3/13

Explanation :

4 kings and 4 queens out of 52 cards.
Thus, 8/52 = 2/13

If a card is picked up at random from a pack of 52 cards. Find the probability that it is ‘a spade’ or ‘a king’ or ‘a queen’

21/52

19/52

17/52

12/52

Explanation :
```
13 spades + 3 kings so 19/52
```

Three coins are tossed. What is the probability of getting 2 Tails and 1 Head

3/8

1/8

7/8

5/8

Explanation :

Event definition is: T and T and H or T and H and T or H and T and T = 3 × 1/8 = 3/8

Three coins are tossed. What is the probability of getting 1 Tail and 2 Heads

7/8

1/8

3/8

5/8

Explanation :
```
Same as above = 3/8.
```

Three coins are tossed. What is the probability of getting neither 3 Heads nor 3 Tails?

3/8

3/4

2/4

1/4

Explanation :

Probability of 3 heads = 1/8
Also, Probability of 3 tails = 1/8.
Required probability = 1– (1/8 + 1/8) = 6/8 = 3/4

Three coins are tossed. What is the probability of getting three heads

7/8

5/8

3/8

1/8

Explanation :
```
H and H and H = 1/8.
```

For the above question, the probability that there is at least one tail is:

1/8

5/8

3/8

7/8

Explanation :

At least one tail is the non-event for all heads.
Thus, P (at least 1 tail) = 1 – P(all heads)
= 1 – 1/8 = 7/8.

Two fair dice are thrown. Find the probability of getting a number divisible by 2 or 4.

1/4

1/6

1/2

1/8

Explanation :

Positive outcomes are 2(1 way), 4(3 ways), 6(5 ways) 8(5 ways), 10 (3 ways), 12 (1way).
Thus, 18/36 = 1/2

Two fair dice are thrown. Find the probability of getting a number divisible by 2 and 4.

1/5

3/4

2/4

1/4

Explanation :

Positive outcomes are: 4, 8 and 12
4 (3 ways), 8(5 ways) and 12(1 way)
Gives us 9/36 = 1/4

Two fair dice are thrown. Find the probability of getting a prime number less than 8

11/36

9/36

7/36

13/36

Explanation :

Positive outcomes are 2(1 way), 3(2 ways), 5(4 ways), 7(6 ways). Total of 13 positive
outcomes out of 36.
Thus, 13/36.

A bag contains 3 green and 7 white balls. Two balls are drawn from the bag in succession without replacement. What is the probability that both are white?

7/15

11/15

5/15

9/15

Explanation :

First is white and second is white 7/10 × 6/9 = 7/15.

A bag contains 3 green and 7 white balls. Two balls are drawn from the bag in succession without replacement. What is the probability that they are of different colour?

7/15

4/15

2/15

1/15

Explanation :

White and Green or Green and White
7/10 × 39 + 3/10 × 7/9
42/90 = 7/15

100 students appeared for two examinations. 60 passed the first, 50 passed the second and 30 passed both. Find the probability that a student selected at random has failed in both the examinations?

4/5

1/5

3/5

2/5

Explanation :


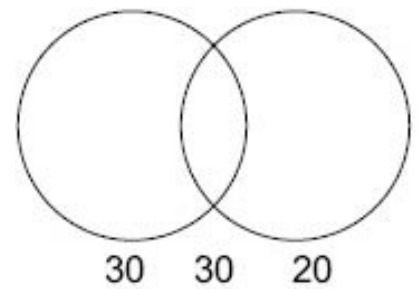From the figure it is evident that 80 students passed at least 1 exam. Thus, 20 failed both and the
required probability is 20/100 = 1/5.

What is the probability of throwing a number greater than 2 with a fair dice?

2/3

2/7

2/23

2/13

Explanation :
```
3 or 4 or 5 or 6 = 4/6 = 2/3
```

Three cards numbered 2, 4 and 8 are put into a box. If a card is drawn at random, what is the probability that the card drawn is (i) a prime number?

1/3

1/33

1/23

1/13

Explanation :

Since 2 is the only prime number out of the three numbers, the answer would be 1/3

Three cards numbered 2, 4 and 8 are put into a box. If a card is drawn at random, what is the probability that the card drawn is (i) an even number?

1/2

1/3

1/4

Explanation :

Since all the numbers are even, it is sure that the number drawn out is an even number.
Hence, the required probability is 1

Three cards numbered 2, 4 and 8 are put into a box. If a card is drawn at random, what is the probability that the card drawn is (i) an odd number?

1/7

1/8

Explanation :

Since there are no odd numbers amongst 2, 4 and 8, the required probability is 0

From a bag containing 4 white and 5 black balls a man draws 3 at random. What are the odds against these being all black?

1/42

17/42

13/42

5/42

Explanation :

Odds against an event = P(E')/P(E)
In this case, the event is: All black, i.e., First is black and second is black and third is black.
P(E) = 5/9 × 4/8 × 3/7 = 60/504 = 5/42.

Amit throws three dice in a special game of Ludo. If it is known that he needs 15 or higher in this throw to win then find the chance of his winning the game.

5/54

17/54

7/54

15/54

Explanation :

Event definition is: 15 or 16 or 17 or 18.
15 can be got as: 5 and 5 and 5 (one way)
Or
6 and 5 and 4 (Six ways)
Or
6 and 6 and 3 (3 ways)
Total 10 ways.
16 can be got as: 6 and 6 and 4 (3 ways)
Or
6 and 5 and 5 (3 ways)
Total 6 ways.
17 has 3 ways and 18 has 1 way of appearing.
Thus, the required probability is: (10 + 6 + 3 + 1)/216 = 20/216 = 5/54

Find out the probability of forming 187 or 215 with the digits 1, 2, 3, 4, 5, 6, 7, 8, 9 when only numbers of three digits are formed and when (i) repetitions are not allowed

1/252

1/2

1/52

1/22

Explanation :

Positive outcomes = 2 (187 or 215)
Total outcomes = 9 × 8 × 7
Required probability = 2/504 = 1/252

In a horse race there were 18 horses numbered 1–18. The probability that horse 1 would win is 1/6, that 2 would win is 1/10 and that 3 would win is 1/8. Assuming that a tie is impossible, find the chance that one of the three will win

47/120

7/120

27/120

17/120

Explanation :
```
1/6 + 1/10 + 1/8 = 47/120
```

Two balls are to be drawn from a bag containing 8 grey and 3 blue balls. Find the chance that they will both be blue.

3/55

33/55

23/55

13/55

Explanation :

The event definition would be given by:
First is blue and second is blue = 3/11 × 2/10 = 3/55

In a certain lottery the prize is ` 1 crore and 5000 tickets have been sold. What is the expectation of a man who holds 10 tickets?

20000

200

2000

Explanation :

Expectation = Probability of winning × Reward of winning = (10/5000) × 1 crore = (1 crore/500)
= 20000.

Two letters are randomly chosen from the word LIME. Find the probability that the letters are L and M.

1/6

5/6

3/6

2/6

Explanation :
```
1/4C2 = 1/6
```

A bag contains four black and five red balls. If three balls from the bag are chosen at random, what is the chance that they are all black?

1/21

17/21

13/21

11/21

Explanation :

Black and Black and Black = 4/9 × 3/8 × 2/7
= 23/504 = 1/21.

If a number of two digits is formed with the digits 2, 3, 5, 7, 9 without repetition of digits, what is the probability that the number formed is 35?

1/20

17/20

13/201/20

11/20

Explanation :
```
1/5P2 = 1/20.
```

From a pack of 52 playing cards, three cards are drawn at random. Find the probability of drawing a king, a queen and jack.

6/5525

76/5525

26/5525

16/5525

Explanation :

6 × (4/52) × (3/51) × (2/50) = 6/5525

A bag contains 20 balls marked 1 to 20. One ball is drawn at random. Find the probability that it is marked with a number multiple of 5 or 7

9/10

7/10

5/10

3/10

Explanation :

Positive Outcomes are: 5, 7, 10, 14, 15 or 20
Thus, 6/20 = 3/10.

A group of investigators took a fair sample of 1972 children from the general population and found that there are 1000 boys and 972 girls. If the investigators claim that their research is so accurate that the sex of a new born child can be predicted based on the ratio of the sample of the population, then what is the expectation in terms of the probability that a new child born will be a girl?

243/ 493

24/ 493

43/ 493

23/ 493

Explanation :
```
972/1972 = 243/ 493
```

A bag contains 3 red, 6 white and 7 black balls. Two balls are drawn at random. What is the probability that both are black?

7/40

37/40

27/40

17/40

Explanation :
```
Black and black = (7/16) × 6/15 = 7/40
```

A and B are two candidates seeking admission to the IIMs. The probability that A is selected is 0.5 and the probability that both A and B are selected is at most 0.3. Is it possible that the probability of B getting selected is 0.9.

yes

cant say

insufficient data

Explanation :

P (Both are selected) = P(A) × P(B)
Since P(A) = 0.5, we get
0.3 = 0.5 × 0.6.
The maximum value of P(B) = 0.6.
Thus P(B) = 0.9 is not possible

The probability that a student will pass in Mathematics is 3/5 and the probability that he will pass in English is 1/3. If the probability that he will pass in both Mathematics and English is 1/8, what is the probability that he will pass in at least one subject?

97/120

17/120

9/120

7/120

Explanation :
```
We have: 19/40 + 1/8 + 5/24 = 97/120
```

The odds in favour of standing first of three students Amit, Vikas and Vivek appearing at an examination are 1 : 2. 2 : 5 and 1 : 7 respectively. What is the probability that either of them will stand first (assume that a tie for the first place is not possible).

125/168

15/168

25/168

12/168

Explanation :

P (Amit) = 1/3
P (Vikas) = 2/7
P (Vivek) = 1/8.
Required Probability = 1/3 + 2/7 + 1/8 = 125/168

A husband and a wife appear in an interview for two vacancies for the same post. The probability of husband’s selection is (1/7) and that of the wife’s selection is 1/5. What is the probability that (i) both of them will be selected?

1/35

11/35

1/3

1/5

Explanation :
```
1/5 × 1/7 = 1/35
```

2/17

6/7

5/7

2/7

Explanation :

(1/5) × (6/7) + (4/5) × (1/7) = 10/35 = 2/7.

24/35

4/35

2/35

14/35

Explanation :
```
(4/5) × (6/7) = 24/35
```

11/35

17/35

13/35

1/35

Explanation :

Both selected or 1 selected = 1/35 + 2/7 = 11/35.

Problems and Solutions

Q. Two unbiased coins are tossed find probability of getting one head ?

A. Sample space = { HH , TT , HT , TH }

P ( atmost one head ) = 3/4 - include case zero heads and 1 heads

P ( atleast one tail) = 3/4 - include case 1 tails and 2 tails

P ( no tails) = 1 / 4

Q. Find the probability of getting sum of faces more than 6 when 2 dies are rolled?

A. Sample space = { (1,1)    (1,2)    (1,3)    (1,4)    (1,5)    (1,6)
(2,1)    (2,2)    (2,3)    (2,4)    (2,5)    (2,6)
(3,1)    (3,2)    (3,3)    (3,4)    (3,5)    (3,6)
(4,1)    (4,2)    (4,3)    (4,4)    (4,5)    (4,6)
(5,1)    (5,2)    (5,3)    (5,4)    (5,5)    (5,6)
(6,1)    (6,2)    (6,3)    (6,4)    (6,5)    (6,6) }

P ( sum more than 6 ) = 21 / 36

P ( sum is multiple of 3 ) = 11 / 36

Q. A bag contains 6 white balls and 4 black balls. Probability that they are of same color.

A. P (event) =

= P (choosing 2 white balls from 6) + P( choosing 2 black from 4)

= (6C2/10C2) + (4C2 / 10C2)

Q. Probability that 2 cards drawn at random from pack of cards are both black, both red , both face cards [queen, king, jack], one face card and other normal, both are aces.

A. n ( sample space ) = sample space size is 52.

P ( both black cards ) = number (black cards) / number (cards) = 26C2/52C2 = 1/2

P ( both red cards ) = 1/2

P ( both face cards) = 12 / 52

P ( one face card and other normal ) = (12C1 * 40C1 ) / 52C2.

P ( both aces ) = 4C2 / 52C2.

Q.There are ten 50 paise coins placed on a table. Six of these show tails, four show heads. A coin is chosen at random and flipped over (not tossed). This operation is performed seven times. One of the coins is then covered. Of the remaining nine coins, five show tails and four show heads. The covered coin shows

a head
a tail
more likely a head
more likely a tail

Ans.a

Quiz

Score more than 80% marks and move ahead else stay back and read again!

Chapter 17: PROBABILITY

Introduction

ANOTHER APPROACH TO LOOK AT THE PROBABILITY PROBLEMS

Solved Question Papers

Problems and Solutions

Quiz

UPSCFEVER - POPULAR PAGES

Join The Movement

Discussions and Comments