-
Chapter 18: SERIES COMPLETION
What value should come in place of question mark (?) in the following number series ?
Ans .
825
Explanation : \(7^{3} + 7, 6^{3} + 6, 5^{3} + 5, 4^{3} + 4\)
Ans .
7397
Explanation : \(36^{2} + 1, 46^{2} + 1, 56^{2} + 1, 66^{2} + 1\)
Ans .
7688
Explanation : 2 x 4, 12 x 24, 22 x 44, 32 x 64.......
Ans .
73935
Explanation : x 1 + 25, x 3 + 75, x 5 + 125, x 7 + 175
Ans .
152839
Explanation : x 9 - 15, x 8 - 14, x 7 - 13, x 6 - 12
Ans .
825
Explanation : \(7^{3} + 7, 6^{3} + 6, 5^{3} + 5, 4^{3} + 4\)
Ans .
If x > y
Explanation : l.\(2x^{2} - 13x - 24\) = 0 \(2x^{2} - 16x + 3x - 24 \)= 0 2x(x - 8) + 3 (x - 8) = 0 (2x + 8) (x - 8) = 0 x = 8, -3/2 ll. \(3y^{2} + 17y + 24\) = 0 \(3y^{2} + 9y + 8y + 24\) = 0 3y(y + 3) + 8 (y + 3) = 0 (y + 3) (3y + 8) = 0 y = -3, -8/3 ∴ x > y
Ans .
7688
Explanation : 2 x 4, 12 x 24, 22 x 44, 32 x 64.......
Ans .
73935
Explanation : \(x^{1} + 25, x^{3} + 75, x^{5} + 125, x^{7} + 175\)
Ans .
152839
Explanation : \(x^{9} - 15, x^{8} - 14, x^{7} - 13, x^{6} - 12\)
Ans .
If x = y or there is no relation between x and y.
Explanation : l. \(x^{2} = 1296\) ll. y = 3√32768
∴ x = +36 ∴ y = 32
Each of these items has a question followed by two statements. As the answer,
Mark (a), If the question can be answered with the help of statement I alone,
Mark (b), If the question can be answered with the help of statement II, alone,
Mark (c), If both, statement I and statement II are needed to answer the question, and
Mark (d), If the question cannot be answered even with the help of both the statements.
Q.Given that X and Y are non-negative. What is the value of X?
I. 2x + 2y ≤ 40
II. x - 2 y ≥ 20
- a
- b
- c
- d
Ans.c
Q.What are the values of 3 integers a, b and c?
I. ab = 8
II. bc = 9
- a
- b
- c
- d
Ans.c
Q.Is the average of the largest and the smallest of four given numbers greater than the average of the
four numbers?
I. The difference between the largest and the second largest numbers is greater than the difference
between the second smallest and the smallest numbers.
II. The difference between the largest and the second largest numbers is less than the difference
between the second largest and the second smallest numbers.
- a
- b
- c
- d
Ans.a
Q.What are the ages of the three brothers?
I. The product of their ages is 21.
II. The sum of their ages is not divisible by 3.
- a
- b
- c
- d
Ans.d
Q.Two types of widgets, namely type A and type B, are produced on a machine. The number of
machine hours available per week is 80. How many widgets of type A must be produced?
I. One unit of type A widget requires 2 machine hours and one unit of type B widget requires 4
machine hours.
II. The widget dealer wants supply of at least 10 units of type A widget per week and he would not
accept less than 15 units of type B widget.
- a
- b
- c
- d
Ans.c
Q.What is the area of a regular hexagon?
I. The length of the boundary line of the hexagon is 36 cm.
II. The area of the hexagon is 6 times the area of an equilateral triangle formed on one of the sides.
- a
- b
- c
- d
Ans.a
Q.What is the price of mangoes per kg?
I. Ten kg of mangoes and two dozens of oranges cost Rs.252.
II. Two kg of mangoes could be bought in exchange for one dozen oranges.
- a
- b
- c
- d
Ans.c
Q.An intelligence agency decides on a code of 2 digits selected from 0, 1, 2, …. , 9. But the slip on which the code is hand–written allows confusion between top and bottom, because these are indistinguishable. Thus, for example, the code 91 could be confused with 16. How many codes are there such that there is no possibility of any confusion?
- 25
- 75
- 80
- none
Ans.c
Q.Suppose one wishes to find distinct positive integers x, y such that (x + y)/ xy is also a positive integer. Identify the correct alternative.
- This is never possible
- This is possible and the pair (x, y) satisfying the stated condition is unique.
- This is possible and there exist more than one but a finite number of ways of choosing the pair (x, y).
- This is possible and the pair (x, y) can be chosen in infinite ways.
Ans.a
Q.Given odd positive integers x, y and z, which of the following is not necessarily true?
- (x2y2z2) is odd
- 3(x2+y3)z2 is even
- 5x+y+z4 is odd
- z2 (x4+y4)/2 is even
Ans.d
Q.A function f(x) is said to be even if f(–x) = f(x), and odd if f(–x) = –f(x). Thus, for example, the function given by f(x) = x2 is even, while the function given by f(x) = x is odd. Using this definition, answer the following questions. The function given by f(x) = |x|3 is
- even
- odd
- neither
- both
Ans.a
Q.A function f(x) is said to be even if f(–x) = f(x), and odd if f(–x) = –f(x). Thus, for example, the function given by f(x) = x2 is even, while the function given by f(x) = x is odd. Using this definition, answer the following questions. The sum of two odd functions
- is always an even function
- is always an odd function
- is sometimes odd and sometimes even
- may be neither odd nor even
Ans.b
Q.ABC forms an equilateral triangle in which B is 2 km from A. A person starts walking from B in a direction parallel to AC and stops when he reaches a point D directly east of C. He, then, reverses direction and walks till he reaches a point E directly south of C. Then D is
- 3 km east and 1 km north of A
- 3 km east and √3 km north of A
- √3 km east and 1 km south of A
- √3 km west and 3 km north of A
Ans.b
Q.ABC forms an equilateral triangle in which B is 2 km from A. A person starts walking from B in a direction parallel to AC and stops when he reaches a point D directly east of C. He, then, reverses direction and walks till he reaches a point E directly south of C.The total distance walked by the person is
- 3 km
- 4 km
- 2 √3 km
- 6 km
Ans.d
This involves recognizing the next term in a series and choosing one from the alternatives given.
Q. 7 , 12 , 19 , X , 39
A. X = 28 as the series follows the pattern: 7, 7+5, 12+7, 19+9, 28+11 where the number is added by the next odd number.
Q. 0, 6, 24, 60, 120, 210, X
A. X = 336 as series follows pattern 13-1 , 23-2 , 33-3 , 43-4....
Q. 4 , 6 , 12 , 14 , 28 , 30 , X
A. There are 2 series in this series 4, 12, 28 ... and 6, 14, 30 and both follow pattern +8, +16, +32, So we get missing value as 28+32 = 60
Q. 1, 4, 9, 16, 25, X
A. Series follows pattern: +3, +5, +7, +9 ...
Q. 20, 19, 17, X, 10, 5
A. Series follows pattern: -1, -2, -3, -4, -5
Q. 6, 11, 21, 36, 56...
A. Pattern: +5, +10, +15, +20, +25...
Q. 1, 6, 13, 22, 33, ...
A. Pattern: +5, +7, +9, +11 ...
Q. 1, 9, 17, 33, 49, 73, X
A. Pattern: + 4 * 2, + 4 * 2, + 4 * 4, + 4 * 4, + 4 * 6, + 4 * 6
Q. 0.5, 1.5, 4.5, 13.5, X
A. Pattern: + 1 , + 1 * 3, + 3 * 3, + 9 * 3 ; Multiply the previous value obtained by 3 each time.
Q. 19, 2, 38, 3, 114, 4, X
A. There are two series: 2, 3, 4, ... and 19, 38, 114, X. The second series follows patterns: * 2, * 3 , * 4, ... So answer is 114*4 = 456
Choose the wrong alternative
A. Series follows pattern: 23 - 1, 33-1, 43-1, 53-1 ... Now we have to check which term doesn't fit this pattern.
Q. 3, 8, 15, 24, 34, 48, 63 ...
A. Series pattern: next term - previous term = 5, 7, 9 ...
Q. 196, 169, 144, 121, 80
A. Pattern: 142, 132, 122, 112 ...
Q. 121, 143, 165, 186, 209
A. Pattern: 112 -02, 122-12, 132-22, 142 - 32, 152 - 42 . Thus odd term is 186.
Q. 1, 2, 4, 8, 16, 32, 64, 96
A. 96 as it is not double of previous
Q. 1, 3, 7, 15, 27, 63, 127
A. Series pattern: +2, +4, +8, +16 .... 27 doesn't follow this pattern.
Q. 6, 14, 30, 64, 126 ...
A. Pattern: +8, +16, +32, +64 and 64 breaks the pattern.
Q. 1236, 2346, 3456, 4566, 5686
A. 5686 breaks the pattern; The first three digits form continuous series so last number should be 5676.
Q. 5, 10, 40, 80, 320, 550, 2560
A. Series follows the pattern: * 2, * 4, * 2, * 4 ....
Q. 11, 2, 21, 3, 32, 4, 41, 5, 51, 6
A. There are two series: 2, 3, 4, 5.. 11 , 21 , 31 , 41 , 51. 32 breaks the second series.
Alphabet Series
Alphabet series sums can be solved using this diagram as reference.
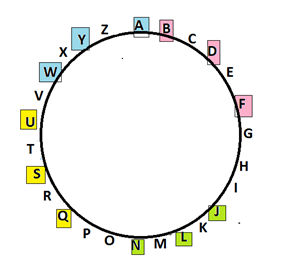
Q. ' ' , ' ', R, T, V, X, Z
A. Series starts from N and skips one alphabet.
Q. P, K, G, D, B, A
A. Series has the pattern: - 5, -4, -3 , -2 ...
Q. BDF, CFI, DHL, ....
A. The first term is moved one place ahead, second two places and third three places.
Q. YEB, WFD, UHG, SKI .....
A. The first term is moved back by 1 then 2 then 3 steps. The second and third terms are moved forward by 1 then 2 then 3 steps. Missing term :QOL
Q. AB, DG, HM, MT, SB, ...
A. The first term is moved ahead in pattern +2, +3, +4 ... The second term is moved ahead in pattern: +4, +5, +6...
Q. P3, R5, T8, V12, ...
A. The first term is moved ahead by +1, +2, +3 and second term by +2, +3, +4 ...
Each of the following questions is followed by two statements. MARK,
- A- if the question can be answered with the help of statement I alone
- B- if the question can be answered with the help of statement II alone ,
- C- if both, statement I and statement II are needed to answer the question
- D- if the statement cannot be answered even with the help of both the statements.
Q.Is it more profitable for Company M to produce Q?
I. Product R is sold at a price four times that of Q.
II. One unit of Q requires 2 units of labour, while one unit of R requires 5 units of labour. There is no
other constraint on production.
- A
- B
- C
- D
Ans.c
Q.A train started from Station A, developed engine trouble and reached Station B, 40 minutes late.
What is the distance between Stations A and B?
I. The engine trouble developed after travelling 40 km from Station A and the speed reduced to 1/4th of the original speed.
II. The engine trouble developed after travelling 40 km from station A in two hours and the speed reduced to 1/4th of the original speed.
- A
- B
- C
- D
Ans.b
Q.What is the value of prime number x?
I. x2 + x is a two digit number greater than 50.
II. x3 is a three digit number.
- A
- B
- C
- D
Ans.a
Q.The average of three unequal quotations for a particular share is Rs.110. If all are quoted in integral
values of rupee, does the highest quotation exceed Rs.129?
I. The lowest quotation is Rs.100.
II. One of the quotations is Rs.115.
- A
- B
- C
- D
Ans.a
Q.How many people (from the group surveyed) read both Indian Express and Times of India?
I. Out of total of 200 readers, 100 read Indian Express, 120 read Times of India and 50 read Hindu.
II. Out of a total of 200 readers, 100 read Indian Express, 120 read Times of India and 50 read
neither.
- A
- B
- C
- D
Ans.b
Q.X says to Y, “I am 3 times as old as you were 3 years ago”. How old is X?
I. Y’s age 17 years from now will be same as X’s present age.
II. X’s age nine years from now is 3 times Y’s present age.
- A
- B
- C
- D
Ans.a
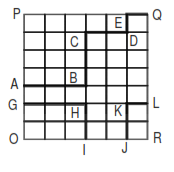
Q.What is the area under the line GHI – JKL in the given quadrilateral OPQR, knowing that all the
small spaces are squares of the same area?
I. Length ABCDEQ is greater than or equal to 60.
II. Area OPQR is less than or equal to 1512.
- A
- B
- C
- D
Ans.c
Q.What is the radius of the circle?
I. Ratio of its area to circumference is greater than 7.
II. Diameter of the circle is less than or equal to 32
- A
- B
- C
- D
Ans.d
Q.What is the time difference between New York and London?
I. The departure time at New York is exactly 9.00 a.m. local time and the arrival time at London is
at 10.00 a.m. local time.
II. The flight time is 5 hours.
- A
- B
- C
- D
Ans.d
Q.Mr. Murthy takes the morning train to his office from station A to station B, and his colleague
Mr.Rahman joins him on the way. There are three stations C, D and E on the way not necessarily in
that sequence. What is the sequence of stations?
I. Mr. Rahman boards the train at D.
II. Mr. Thomas, who travels between C & D has two segments of journey in common with
Mr. Murthy but none with Mr. Rahman.
- A
- B
- C
- D
Ans.c
Q.If R is an integer between 1 & 9, P – R = 2370, what is the value of R?
- P is divisible by 4.
- P is divisible by 9.
Ans
- A
- B
- C
- D
Q.A man distributed 43 chocolates to his children. How many of his children are more than five years old?
- A child older than five years gets 5 chocolates.
- A child 5 years or younger in age gets 6 chocolates.
Ans
- A
- B
- C
- D
Q.Ramu went by car from Calcutta to Trivandrum via Madras, without any stoppages. The average speeds for the entire journey was 40 kmph. What was the average speed from Madras to Trivandrum?
- The distance from Madras to Trivandrum is 0.30 times the distance from Calcutta to Madras.
- The average speed from Madras to Trivandrum was twice that of the average speed from Calcutta to Madras.
Ans
- A
- B
- C
- D
Q.x, y and z are three positive odd integers, is x + z divisible by 4?
- y – x = 2
- z – y = 2.
Ans
- A
- B
- C
- D
Q.The unit price of product P1 is non-increasing and that of product P2 is decreasing. Which product will be costlier 5 years hence?
- Current unit price of P1 is twice that of P2.
- 5 years ago, unit price of P2 was twice that of P1.
Ans
- A
- B
- C
- D
Q.X is older than Y, Z is younger than W and V is older than Y. Is Z younger than X?
- W may not be older than V.
- W is not older than V.
Ans
- A
- B
- C
- D
Q.How long did Mr. X take to cover 5000 km journey with 10 stopovers?
- the ithlasted i2minutes
- the average speed between any two stopovers was 66 kmph.
Ans
- A
- B
- C
- D
Q.Is (x-1 - y -1) / (x-2 - y-2)
- x + y is greater than 0.
- x and y are positive integers and each is greater than 2.
Ans
- A
- B
- C
- D
Answer Key
| 1-b | 2-c | 3-c | 4-c | 5-d | 6-d | 7-d | 8-b |
Q. In a game played by two people there were initially N match sticks kept on the table. A move in the game consists of a player removing either one or two matchsticks from the table. The one who takes the last matchstick loses. Players make moves alternately. The player who will make the first move is A. The other player is B.The smallest value of N (greater than 5) that ensures a win for B is
- 7
- 6
- 10
- 8
Ans.A
Q.In a game played by two people there were initially N match sticks kept on the table. A move in the game consists of a player removing either one or two matchsticks from the table. The one who takes the last matchstick loses. Players make moves alternately. The player who will make the first move is A. The other player is B.The largest value of N (less than 50) that ensures a win for B is
- 46
- 47
- 48
- 49
Ans.D
Q.There were x pigeons and y mynahs in a cage. One fine morning p of them escaped to freedom. If the bird keeper, knowing only that p = 7, was able to figure out without looking into the cage that at least one pigeon had escaped, then which of the following does not represent a possible (x,y) pair?
- (10,8)
- (7,2)
- (25,6)
- 12,4
Ans.a
Q.Mr.X enters a positive integer Y in an electronic calculator and then goes on pressing the square – root key repeatedly. Then
- The display does not stabilize
- The display becomes closer to 0
- The display becomes closer to 1
- May not be true and the answer depends on the choice of Y
Ans.c
Q.Consider the following steps :
1. Put x = 1, y = 2
2. Replace x by xy
3. Replace y by y +1
4. If y = 5 then go to step 6 otherwise go to step 5.
5. Go to step 2
6. Stop
Then the final value of x equals
- 1
- 24
- 720
- 120
Ans.b
Q.From any two numbers x and y, we define x × y = x + 0.5y – xy. Suppose that both x and y are greater than 0.5. Then x × x < y × y if
- 1 > x > y
- x > 1 > y
- 1 > y > x
- y > 1 > x
Ans.b
Q.Consider a function f(k) defined for positive integers k = 1, 2, …. ; the function satisfies the condition f(1) + f(2) + ... = P / (p-1). where 0 < p < 1.Then f(k) is given by
- p(–p) k–1
- p(1–p)k-1
- {p(1–p)}k–1
- None of these
Ans.a
Q.The value of (1-d3) / (1-d) is
- > 1 if d > –1
- > 3 if d > 1
- > 2 if 0 < d < 0.5
- < 2 if d < –2
Ans.b
Q.A dealer deals only in colour TVs and VCRs. He wants to spend up to Rs.12 lakhs to buy 100 pieces. He can purchase a colour TV at Rs.10,000 and a VCR at Rs.15,000. He can sell a colour TV at Rs.12,000 and a VCR at Rs.17,500. His objective is to maximize profits. Assume that he can sell all the items that he stocks.For the maximum profit, the number of colour TVs and VCRs that he should respectively stock are
- 80, 20
- 20, 80
- 60, 40
- None of these
Ans.c
Q.A dealer deals only in colour TVs and VCRs. He wants to spend up to Rs.12 lakhs to buy 100 pieces. He can purchase a colour TV at Rs.10,000 and a VCR at Rs.15,000. He can sell a colour TV at Rs.12,000 and a VCR at Rs.17,500. His objective is to maximize profits. Assume that he can sell all the items that he stocks.If the dealer would have managed to get an additional space to stock 20 more items, then for maximizing profit, the ratio of number of VCRs and number of TVs that he should stock is
- 7 : 3
- 0
- 1:2
- None of these
Ans.b
Q.A dealer deals only in colour TVs and VCRs. He wants to spend up to Rs.12 lakhs to buy 100 pieces. He can purchase a colour TV at Rs.10,000 and a VCR at Rs.15,000. He can sell a colour TV at Rs.12,000 and a VCR at Rs.17,500. His objective is to maximize profits. Assume that he can sell all the items that he stocks.The maximum profit, in rupees lakh, the dealer can earn from his original stock if he can sell a colour TV at Rs. 12200 and VCR at Rs.18300 is
- 2.64
- 2.49
- 2.72
- 2.87
Ans.a
The following questions relate to a game to be played by you and your friend. The game consists of a 4 x 4 board (see below) where each cell contains a positive integer. You and your friend make moves alternately. A move by any of the players consists of splitting the current board configuration into two equal halves and retaining one of them. In your moves you are allowed to split the board only vertically and to decide to retain either the left or the right half. Your friend, in his/her moves, can split the board only horizontally and can retain either the lower or the upper half. After two moves by each player a single cell will remain which can no longer be split and the number in that cell will be treated as the gain (in rupees) of the person who has started the game. A sample game is shown below.
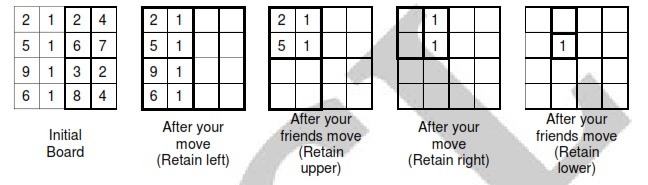
So your gain is Re.1. With the same initial board configuration as above and assuming that you have to make the first move, answer the following questions.
Q.If you choose (retain right) (retain left) in your turns, the best move sequence for your friend to reduce your gain to a minimum will be
- (retain upper)(retain lower)
- (retain lower) (retain upper)
- (retain upper) (retain upper)
- (retain lower) (retain lower
Ans:c
Q.If both of you select your moves intelligently then at the end of the game your gain will be
- Rs.4
- Rs.3
- Rs.2
- None of these
Ans:b
Q.If your first move is (retain right), then whatever moves your friend may select you can always force a gain of no less than
- Rs.3
- Rs.6
- Rs.4
- None of these
Ans:a
Q.N the set of natural numbers is partitioned into subsets S 1 = (1), S 2 = (2, 3), S3 ={4, 5, 6), S4 = {7, 8, 9, 10} and so on. The sum of the elements of the subset S50 is
- 61250
- 65525
- 42455
- 62525
Ans:d
Q.A square is drawn by joining the midpoints of the sides of a given square. A third square is drawn inside the second square in the same way and this process is continued indefinitely. If side of the first square is 8 cm, the sum of the areas of all the squares such formed (in sq.cm.) is
- 128
- 120
- 96
- None of these
Ans:a
Q.There are 5 cities, A, B, C, D and E connected by 7 roads as shown in the figure below:Design a route such that you start from any city of your choice and walk on each of the 7 roads once and only once, not necessarily returning to the city from which you started.
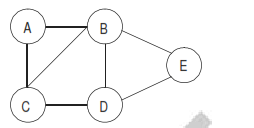
Q.For a route that satisfies the above restrictions, which of the following statements is true?
- There is no route that satisfies the above restriction.
- A route can either start at C or end at C, but not both
- D can be only an intermediate city in the route.
- The route has to necessarily end at E.
Ans:b
Q.How many different starting cities are possible such that the above restriction is satisfied?
- 1
- 0
- 3
- 2
Ans:d
Q.if xy + yz + zx = 0, then (x + y + z)2 equals
- (x+y)2+xz
- (x+z)2+xy
- x2+y2+z2
- 2(xy + yz + xz)
Ans:c
Q.If equal numbers of people are born on each day, find the approximate percentage of the people whose birthday will fall on 29 th February. (If we are to consider people born in 20 century and assuming no deaths).
- 0.374
- 0.5732
- 0.0664
- None of these
Ans:d
@ (A, B) = average of A and B
*(A, B) = product of A and B
/(A, B) = A divided by B
Answer these questions with the above data.
Q.If A = 2 and B = 4, the value of @(/(*(A, B), B), A) would be
- 2
- 4
- 6
- 16
Ans.a
Q.The sum of A and B is given by
- *(@(A, B), 2)
- /(@(A, B), 2)
- @(*(A, B), 2)
- @(/(A, B), 2)
Ans.a
Q.The sum of A, B, and C is given by
- *(@(*(@(B, A), 2), C), 3)
- /(@(*(@(B, A), 3), C), 2)
- /(*(@(*(B, A), 2), C), 3)
- None of these
Ans.a
Read and Answer
Mark (a), If the question can be answered with the help of statement I alone,
Mark (b), If the question can be answered with the help of statement II, alone,
Mark (c), If both, statement I and statement II are needed to answer the question, and
Mark (d), If the question cannot be answered even with the help of both the statements.
Q.Is the distance from the office to home less than the distance from the cinema hall to home?
I. The time taken to travel from home to office is as much as the time taken from home to the
cinema hall, both distance being covered without stopping.
II. The road from the cinema hall to home is bad and speed reduces, as compared to that on the
road from home to the office.
- a
- b
- c
- d
Ans.c
Q.A and B work at digging a ditch alternately for a day each. If A can dig a ditch in ‘a’ days and B can
dig that ditch in ‘b’ days, will work get done faster if A begins the work?
I. n is a positive integer such that n(1/a + 1/b) =1
II. b > a
- a
- b
- c
- d
Ans.a
Q.If twenty sweets are distributed among some boys and girls such that each girl gets two sweets and
each boy gets three sweets, what is the number of boys and girls?
I. The number of girls is not more than five.
II. If each girl gets 3 sweets and each boy gets 2 sweets, the number of sweets required for the
children will still be the same.
- a
- b
- c
- d
Ans.b
Q.If the selling price were to be increased by 10%, the sales would reduce by 10%. In what ratio would
profits change?
I. The cost price remains constant.
II. The cost price increased 10%.
- a
- b
- c
- d
Ans.b
Q.What is the average weight of the 3 new team members who are recently included into the team?
I. The average weight of the team increases by 20 kg.
II. The 3 new men substitute earlier members whose weights are 64 kg, 75 kg and 66 kg
- a
- b
- c
- d
Ans.d
Q.Is segment PQ greater than segment RS?
I.
PB > RE,BQ = ES.
II. B is a point on PQ, E is a point on RS.
- a
- b
- c
- d
Ans.c
Q.Three boys had a few coffee Bite toffees with them. The number of toffees with the second were four
more than those with the first and the number of toffees with the third were four more than those with
the second. How many toffees were there in all?
I. The number of toffees with each of them is a multiple of 2.
II. The first boy ate up four toffees from what he had and the second boy ate up six toffees from
what had and the third boy gave them two toffees each from what he had and the number of
toffees remaining with each of them formed a geometric progression.
- a
- b
- c
- d
Ans.b
Q.Little Beau Peep lost her sheep. She couldn’t remember how many were there. She knew she
would have 400 more next year, than the number of sheep she had last year. How many sheep were
there?
I. The number of sheep last year was 20% more than the year before that and this rate of increase
continues to be the same for the next 10 years.
II. The increase is compounded annually.
- a
- b
- c
- d
Ans.c
Q.What will be the total cost of creating a 1- foot border of tiles along the inside edges of a room?
I. The room is 48 feet in length and 50 fet in breadth.
II. Every tile costs Rs. 10
- a
- b
- c
- d
Ans.d
Q.Ten boys go to a neighbouring orchard. Each boy steals a few mangoes. What is the total number
of mangoes they steal?
I. The first boy steals 4 mangoes and the fourth boy steals 16 mangoes and the eight boy 32
mangoes and the tenth boy steals 40 mangoes.
II. The first boy stole the minimum number of mangoes and the tenth boy stole the maximum
number of mangoes.
- a
- b
- c
- d
Ans.d
Q.A, S, M and D are functions of x and y, and they are defined as follows.
A(x, y) = x + y
S(x, y) = x – y
M(x, y) = xy
D(x, y) = x/y ; y ≠ 0
What is the value of M(M(A(M(x, y), S(y, x)), x), A(y, x)) for x = 2, y = 3?
60
140
25
70
Ans.d
Q.What is the value of S[M(D(A(a, b), 2), D(A(a, b), 2)), M(D(S(a, b), 2), D(S(a, b), 2))]?
a2+b2
ab
a2-b2
a/b
Ans.b
Q.Given the quadratic equation x2 - (A-3)x - (A-2)=0; for what value of A will the sum of the squares of the roots be zero?
-2
3
6
none
Ans.d
Read and solve
The Weirdo Holiday Resort follows a particular system of holidays for its employees. People are given holidays on the days where the first letter of the day of the week is the same as the first letter of their names. All employees work at the same rate.
Q.Raja starts working on February 25, 1996, and finishes the job on March 2, 1996. How much time would T and J take to finish the same job if both start on the same day as Raja?
4 days
5 days
Either (a) or (b)
Cannot be determined
Ans.c
Q.Starting on February 25, 1996, if Raja had finished his job on April 2, 1996, when would T and S together likely to have completed the job, had they started on the same day as Raja?
March 15, 1996
March 14, 1996
March 22, 1996
Data insufficient
Ans.c
Chapter Review
Score more than 80% marks and move ahead else stay back and read again!