AVERAGE - Aptitude

Chapter 5: AVERAGE

Introduction

Average is the mean value of a set of numbers.

Average = (x₁+x₂+x₃+...+x_n) / N.

E.g: If the weight of 4 students is 20,22,18,24 then their average weight is 20+22+18+24 = 84 / 4 = 21.

Weighted average is the average of two or more groups whose individual averages are known.

W . A = (n1*a1 + n2 * a2) / (n1 + n2)
n1= strength of group 1
n2 = strength of group 2
a1 = average of group 1
a2 = average of group 2

Average speed: Ratio of total distance to the total time taken.

Method to calculate average speed taken

Step 1:Average speed = (2S1 * S2)/(S1 + S2) [S1 and S2 are speeds]

Step 2:

The ratio of speeds is 60 : 100 = 3 : 5 (say r₁: r₂) Then, divide the difference of speeds (40 in this case) by r₁ + r₂ (3 + 5 = 8, in this case) to get one part. (40/8 = 5, in this case)

The required answer will be three parts away (i.e. r₁ parts away) from the lower speed

Example : Ratio of speeds = 20 : 40 = 1 : 2

Divide difference of 20 into 3 parts (r₁ + r₂) = 20/3 = 6.66. Required average speed = 20 + 1 × 6.66

Age and average: If the average age of 'n' persons decreased by 'a' years , then the total age is decreased by 'n*a' years.

Average of 'n' consecutive odd numbers is the middle value i.e. average of 1,3,5,7,9 is 5. Average of 'n' consecutive even numbers is the average of two middle numbers i.e. 2,4,6,8,10,12 is 6+8/2 = 7.

E.g: The average weight of 6 men is reduced by 3 kg when a man weighing 60 kg is replaced by another man, so find his weight?
A. Decrease in average weight = 3 kg, decrease in total weight = 6*3 = 18. Therefore weight of the new man = 60 - 18 = 42.

Rule of Alligation:
If two quantities are mixed in a ratio then

Quantity of cheaper / Quantity of dearer =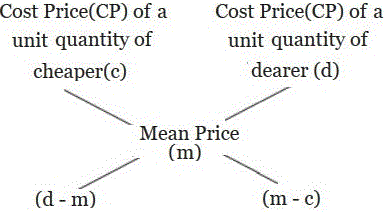

alligation problems in aptitude

A man travels at 60 kmph on the journey from A to B and returns at 100 kmph. Find his average speed for the journey

Ans .

Explanation :

Average speed = (total distance)/(total time).
If we assume distance between 2 points to be "d"
Then Average speed = 2d/[(d/60) + (d/100)] = (2 × 60 × 100)/ (60 + 100) = (2 × 60 × 100)/160 = 75

If the average age of a group of persons is x years today then after n years their average age will be

x*n

x+n

x-n

Ans .

x+n

Explanation :

If the average age of a group of persons is x years today then after n
years their average age will be (x + n).

The average of a batsman after 25 innings was 56 runs per innings. If after the 26th inning his average increased by 2 runs, then what was his score in the 26th inning?

100

102

104

108

Ans .

Explanation :

Since the average increases by 2 runs per innings it is equivalent to 2 runs being added to each
score in the first 25 innings. Now, since these runs can only be added by the runs scored in the 26th
inning, the score in the 26th inning must be 25 × 2 = 50 runs higher than the average after 26 innings (i.e.
new average = 58).
Hence, runs scored in 26th inning = New Average + Old innings × Change in average
= 58 + 25 × 2 = 108

The average age of a class of 30 students and a teacher reduces by 0.5 years if we exclude the teacher. If the initial average is 14 years, find the age of the class teacher

Ans .

Explanation :

The teacher after fulfilling the average of 14 (for the group to which he belonged) is also able
to give 0.5 years to the age of each of the 30 students. Hence, he has 30 × 0.5 = 15 years to give over and
above maintaining his own average age of 14 years.
Age of teacher = 14 + 30 × 0.5 = 29 years

The average marks of a group of 20 students on a test is reduced by 4 when the topper who scored 90 marks is replaced by a new student. How many marks did the new student have?

Ans .

Explanation :

The replacement has the effect of reducing the average marks for each of the 20 students by 4. Hence, the replacement must be 20 × 4 = 80 marks below the original.
Hence, answer = 10 marks.

The average age of 3 students A, B and C is 48 marks. Another student D joins the group and the new average becomes 44 marks. If another student E, who has 3 marks more than D, joins the group, the average of the 4 students B, C, D and E becomes 43 marks. Find how many marks A got in the exam.

Ans .

Explanation :

The first sentence gives you a total of 144 for A, B and C’s marks. Second
sentence: When D joins the group, the total becomes 44 × 4 = 176. Hence D must get 32 marks.
Alternatively, you can reach this point by considering the first 2 statements together as:
D’s joining the group reduces the average from 48 to 44 marks (i.e. 4 marks).
This means that to maintain the average of 44 marks, D has to take 4 marks from A, 4 from B and 4 from C
Æ A total of 12 marks. Hence, he must have got 32 marks.
From here:
The first part of the third sentence gives us information about E getting 3 marks more than 32 Æ Hence, E
gets 35 marks.
Now, it is further stated that when A is replaced by E, the average marks of the students reduces by 1 to
43.
Mathematically this can be shown as
A + B + C + D = 44 × 4 = 176 while, B + C + D + E
= 43 × 4 = 172
Subtracting the two equations, we get A – E = 4 marks.
Hence, A would have got 39 marks.
Alternatively, you can think of this as:
The replacement of A with E results in the reduction of 1 mark from each of the 4 people who belong to
the group. Hence, the difference is 4 marks. Hence, A would get 4 marks more than E i.e. A gets 39 marks.

The mean temperature of Monday to Wednesday was 27 °C and of Tuesday to Thursday was 24 °C. If the temperature on Thursday was 2/3rd of the temperature on Monday, what was the temperature on Thursday?

Ans .

Explanation :

we get that the total from Monday to Wednesday was 81 while from
Tuesday to Thursday was 72. The difference is arising out of the replacement of Monday by Thursday.
This can be mathematically written as
Mon + Tue + Wed = 81
Tue + Wed + Thu = 72
Hence, Mon – Thu = 9
Thu = (2/3) × Mon; thus we get Thursday = 18 °C

A school has only 3 classes that contain 10, 20 and 30 students respectively. The pass percentage of these classes are 20% , 30% and 40% respectively. Find the pass percentage of the entire school.

Ans .

Explanation :
using weighted average : \( \frac{10 * 0.2 + 20*0.3 + 30*0.4}{10+20+30} = 20/60 = 33.33%\)

The average age of 24 students and the principal is 15 years. When the principal’s age is excluded, the average age decreases by 1 year. What is the age of the principal?

Ans .

Explanation :

P = 25 × 15 – 24 × 14 = 375 – 336 = 39

The average weight of 3 men A, B and C is 84 kg. Another man D joins the group and the average now becomes 80 kg. If another man E, whose weight is 3 kg more than that of D, replaces A then the average weight of B, C, D and E becomes 78 kg. The weight of A is

Ans .

Explanation :

D’s weight = 4 × 80 – 3 × 84 = 320 – 252 = 68. E’s weight = 68 + 3 = 71.
Now, we know that A + B + C + D = 4 × 80 = 320 and B + C + D + E = 78 × 4 = 312. Hence, A’s
weight is 8 kg more than E ’s weight. A = 71 + 8 = 79.

Three years ago, the average age of A, B and C was 27 years and that of B and C 5 years ago was 20 years. A’s present age is

Ans .

Explanation :

Today’s total age of A, B and C = 30 × 3 = 90.
Today’s total age for B and C = 25 × 2 = 50.
C ’s age = 90 – 50 = 40

Find the average of all prime numbers between 30 and 50?

39.8

38.8

37.8

36.8

Ans .

39.8

Explanation :

there are five prime numbers between 30 and 50.
        They are 31,37,41,43 and 47.
 Therefore the required average=(31+37+41+43+47)/5  So 199/5  = 39.8

find the average of first 40 natural numbers?

20.5

18.5

24.5

22.5

Ans .

20.5

Explanation :

sum  of first n natural numbers=n(n+1)/2;
 So,sum of 40 natural numbers=(40*41)/2  which is 820.
 Therefore  the required average=(820/40) which is 20.5.

find the average of first 20 multiples of 7?

75.5

76.5

73.5

77.5

Ans .

73.5

Explanation :

Required average =7(1+2+3+…….+20)/20   which is (7*20*21)/(20*2) which is (147/2)= 73.5.

the average of four consecutive even numbers is 27. find the largest of these numbers?

Ans .

Explanation :

let the numbers be x,x+2,x+4 and x+6. then,
(x+(x+2)+(x+4)+(x+6))/4) = 27  
i.e. (4x+12)/4 = 27
i.e. x+3=27      i.e.  x=24.
Therefore the largest number=(x+6)=24+6=30

there are two sections A and B of a class consisting of 36 and 44 students respectively. If the average weight of section A is 40kg and that of section B is 35kg, find the average weight of the whole class?

35.25

33.25

47.25

37.25

Ans .

37.25

Explanation :

total weight of(36+44) students=(36*40+44*35)kg  =2980kg.
 Therefore weight of the total class=(2980/80)kg  = 37.25kg

nine persons went to a hotel for taking their meals 8 of them spent Rs.12 each on their meals and the ninth spent Rs.8 more than the average expenditure of all the nine.What was the total money spent by them?

113

115

117

119

Ans .

Explanation :

Let the average expenditure of all nine be Rs.x
Then 12*8+(x+8)=9x or 8x=104 or x=13.
Total money spent = 9x=Rs.(9*13)=Rs.117

Of the three numbers, second is twice the first and is also thrice the third.If the average of the three numbers is 44.Find the largest number.

Ans .

Explanation :

Let the third number be x.
Then second number = 3x.
First number=3x/2.
Therefore x+3x+(3x/2)=(44*3) or x=24
So largest number= 2nd  number = 3x = 72

The average of 25 result is 18.The average of 1st 12 of them is 14 & that of last 12 is 17.Find the 13th result.

Ans .

Explanation :

Clearly 13th result = (sum of 25 results)-(sum of 24 results)
=(18*25)-(14*12)+(17*12)
=450-(168+204)
=450-372
=78

The Average of 11 results is 16, if the average of the 1st 6 results is 58 & that of the last six 63. Find the 6th result

Ans .

Explanation :

: 6th result = (58*6 + 63*6 - 60*11) = 66

The average waight of A,B,C is 45 Kg. The avg wgt of A & B be 40Kg & that of B,C be 43Kg. Find the wgt of B.

Ans .

Explanation :

Let A,B,c represent their individual wgts.
Then,
A+B+C=(45*3)Kg=135Kg
A+B=(40*2)Kg=80Kg & B+C=(43*2)Kg=86Kg
B=(A+B)+(B+C)-(A+B+C)
=(80+86-135)Kg
=31Kg

The average age of a class of 39 students is 15 years. If the age of the teacher be included, then the average increases by3 months. Find the age of the teacher.

Ans .

Explanation :

Total age of 39 persons = (39 x 15) years  = 585 years.
Average age of 40 persons = 15 yrs 3 months  = 61/4 years.
Total age of 40 persons = (_(61/4 )x 40) years= 610 years. 
:. Age of the teacher = (610 - 585) years = 25 years.

The average weight of 10 oarsmen in a boat is increased by 1.8 kg when one of the crew, who weighs 53 kg is replaced by a new man. Find the weight of the new man.

Ans .

Explanation :

Total weight increased =(1.8 x 10) kg =18 kg.
:. Weight of the new man =(53 + 18) kg = 71 kg

There were 35 students in a hostel. Due to the admission of 7 new students, ;he expenses of the mess were increased by Rs. 42 per day while the average expenditure per head diminished by Rs 1. Wbat was the original expenditure of the mess?

420

430

460

440

Ans .

Explanation :

Let the original average expenditure be Rs. x. Then,
 42 (x - 1) - 35x=42   -> 7x= 84 -> x =12.
Original expenditure = Rs. (35 x 12) = Rs. 420.

A batsman makes a score of 87 runs in the 17th inning and thus increases his avg by 3. Find his average after 17th inning

Ans .

Explanation :

Let the average after 17th inning = x.
 Then, average after 16th inning = (x - 3).
:. 16 (x - 3) + 87 = 17x or x = (87 - 48) = 39

Distance between two stations A and B is 778 km. A train covers the journey from A to B at 84 km per hour and returns back to A with a uniform speed of 56 km perhour. Find the average speed of the train during the whole journey.

73.2

67.2

71.2

69.2

Ans .

67.2

Explanation :

Required average speed = ((2xy)/(x+y)) km / hr 
=(2 x 84 x 56)/(84+56)km/hr
 = (2*84*56)/140 km/hr
= 67.2 km/hr

E.g: In what proportion must rice at Rs3.10 per kg be mixed with rice at Rs3.60 per kg, so that the mixture be worth Rs3.25 a kg?
A. c = 3.10 , d = 3.6 , m = 3.25.
Therefore, quantity of cheaper / quantity of dearer =
= (d-m):(m-c) = (3.6-3.25): (3.25-3.1)
= 7:3.

Rule of Mixtures: If a container having 'V' units of a liquid in a solution and 'k' units of liquid is taken out and replaced by 'k' units of water and this operation is repeated 'n' times then the final quantity of liquid in container is given by

Q = V * ( 1 - (k/V) ) ^ ⁿ

E.g: For a container with 120 liters of milk, 40 liters is taken out and replaced with water. If this process is repeated twice, find the quantity of milk in the container now.
A. Quantity of milk in the container: = 120 ( 1 - (40/120)) ^ ²

= 120 * (4 / 9) = 53.33 liters.

Sample Questions

Q. If average age of 10 people is 32 what must be the age of the new joinee if the average age increases by 5.

A. Old average = 10*32=320, New average = 11 * 37 = 407 so new joinee must have age = 407 - 320 = 87.

Q. there are two sections A and B of a class consisting of 36 and 44 students respectively. If the average weight of section A is 40kg and that of section B is 35kg, find the average weight of the whole class?

A. n1 =36, n2 = 44, a1 = 40 , a2 = 35 now apply weighted average formula (see above).

Q. Nine persons went to a hotel for taking their meals 8 of them spent Rs. 12 each on their meals and the ninth spent Rs. 8 more than the average expenditure of all the nine. What was the total money spent by them?

A. Let 'x' be the average. The equation is 12*8 + (x+8) = 9*x as total sum spent by all 9 is addition of Rs. 12 each spent by first 8 i.e. 12*8 and the Rs. 8 more than average spent by last one i.e. x+8.

Q. The average age of a class of 39 students is 15 years. If the age of the teacher be included, then the average increases by 3 months. Find the age of the teacher.

A. The teachers age = (Group average) + (increase in average age of entire group)

= 15 yrs + ( 40 * 3 months)

= 15 yrs + (120 months / 10 yrs)

= 25 years

Q. The average weight of 10 oarsmen in a boat is increased by 1.8 kg when one of the crew, who weighs 53 kg is replaced by a new man. Find the weight of the new man.

A. Weight of new man = 53 + (1.8*10) = 53 + 18 = 71 kg.

Q. There were 35 students in a hotel. Due to the admission of 7 new students, ; the expenses of the hotel were increased by Rs. 42 per day while the average expenditure per student diminished by Rs 1. What was the original expenditure of the hotel?

A. Let original average expenditure per student be 'x'.

So we get 42(x-1) - 35x = 42. As for 42 students the average expense decreased by 1 and so total was 42*(x-1) and for 35 students it was 35x.

Q. Distance between two stations A and B is 200 km. A train covers the journey from A to B at 100 km per hour and returns back to A with a uniform speed of 50 km per hour. Find the average speed of the train during the whole journey.

A. time taken to go from A to B = 2 hrs and from B to A is 4 hrs.

Average speed = total distance / total time = 400 / (2+4) km/hr

Directly use formula 2xy / (x+y) where x = speed from A to B, y = speed from B to A.

average speed = 2*100*50 / (100+50) = 400 / 6 km/hr

Q. In what ratio must rice at Rs. 9.30 per kg be mixed with rice at Rs. 10.80 per kg so that the mixture be worth Rs. 10 per kg ?

A. d = 10.8, c = 9.3 and m = 10

Quantity of cheaper / Quantity of dearer = (10.8 - 10)/(10-9.3) = 8/7

Q. How much water must be added to 60 litres of milk at 1 ½ litres for Rs. 20 So as to have a mixture worth Rs.10 2/3 a litre ?

A. 1 liter milk = 40/3 rupees

Quantity of milk / quantity of water = (32/3 - 0 ) / (40/3 - 32/3) = (32/3:8/3)

So 4:1

Q. How many kgs. of wheat costing Rs. 8 per kg must be mixed with 36 kg of rice costing Rs. 5.40 per kg so that 20% gain may be obtained by selling the mixture at Rs. 7.20 per kg ?

A. If selling price is 7.2 then cost price is 6 as 20% gain is made.

quantity of rice / wheat = (6 - 5.4) / (8-6) = 0.6 / 2 = 3/10.

So for 3 kg of rice 10kg of wheat is needed so we need x kg of wheat for 36 kg of rice. 3:10 :: 36:x

x = 36*10 / 3 = 120 kg

Quiz

Score more than 80% marks and move ahead else stay back and read again!

Q1: The average weight of 6 men is reduced by 3 kg when a man weighing 60 kg is replaced by another man, so find his weight?

Q2: In what proportion must rice at Rs3.10 per kg be mixed with rice at Rs3.60 per kg, so that the mixture be worth Rs3.25 a kg?

3/7

14/3

17/3

7/3

Q3: For a container with 120 liters of milk, 40 liters is taken out and replaced with water. If this process is repeated twice, find the quantity of milk in the container now.

53.33

56.33

63.33

59.33

Q4: If average age of 10 people is 32 what must be the age of the new joinee if the average age increases by 5.

Q5: Nine persons went to a hotel for taking their meals 8 of them spent Rs. 12 each on their meals and the ninth spent Rs. 8 more than the average expenditure of all the nine. What was the total money spent by them?

upscfever.com

Chapter 5: AVERAGE

Introduction

Solved Question Papers

Solved Question Papers

= 120 * (4 / 9) = 53.33 liters.

Sample Questions

Quiz

UPSCFEVER - POPULAR PAGES

Join The Movement

Discussions and Comments