Alligations

ALLIGATIONS

If \( A_1, A_2, A_3, ..., A_n \) are the groups of people with total members \( n_1, n_2, .. ,n_n \)

Then the weighted average is given by \( \frac{n_1*A_1 + n_2*A_2 + ... + n_n*A_n}{n_1 + n_2 + .. + n_n} \)

Assume two groups are there we can rewrite average as Aw = \( \frac{n_1A_1 * n_2*A_2}{n_1*n_2} \)

We rewrite the equation as : (\( n_1 * n_2 \))Aw = \(n_1A_1 + n_2A_2\)

\( n_1(Aw - A_1) = n_2(A_2 - Aw)\)

or \( \frac{n_1}{n_2} = \frac{A_2 - Aw}{Aw - A_1}\). This is the Alligation equation.

The Alligation Situation

Two groups of elements are mixed together to form a third group containing the elements of both the groups

If the average of the first group is A₁ and the number of elements is n₁ and the average of the second group is A₂ and the number of elements is n₂ , then to find the average of the new group formed, we can use either the weighted average equation or the alligation equation.

As a convenient convention, we take A₁ < A₂ . Then, by the principal of averages, we get A₁ < Aw < A₂ .

Some Keys to spot A₁, A₂ and A_w and differentiate these from n₁ and n₂

Normally, there are 3 averages mentioned in the problem, while there are only 2 quantities. This isn’t foolproof though, since at times the question might confuse the student by giving 3 values for quantities representing n₁ , n₂ and n₁ + n₂ respectively

A₁ , A₂ and Aw are always rate units, while n₁ and n₂ are quantity units.

The denominator of the average unit corresponds to the quantity unit (i.e. unit for n₁ and n₂ ).

All percentage values represent the average values.

Two varieties of rice at ` 10 per kg and ` 12 per kg are mixed together in the ratio 1 : 2. Find the average price of the resulting mixture

11.33

11.45

Ans .

11.33

Explanation :

1/2 = (12 – Aw)/(Aw – 10) Æ Aw – 10 = 24 – 2Aw
fi 3Aw = 34 fi Aw = 11.33 `/kg

On combining two groups of students having 30 and 40 marks respectively in an exam, the resultant group has an average score of 34. Find the ratio of the number of students in the first group to the number of students in the second group.

3/2

4/5

1/2

4/9

Ans .

3/2

Explanation :

n1
/n2 = (40 – 34)/(34 – 30) = 6/4 = 3/2

Case 1: A1, A2, Aw are known; may be one of n1 or n2 is known. To find : n1 : n2 and n2 if n1 is known OR n1 if n2 is known

On mixing two classes of students having average marks 25 and 40 respectively, the overall average obtained is 30 marks. Find The ratio of students in the classes

6 : 1

2 : 3

2 : 1

3 : 1

Ans .

2 : 1

Explanation :
```
Hence, solution is 2 : 1
```

On mixing two classes of students having average marks 25 and 40 respectively, the overall average obtained is 30 marks. Find The number of students in the first class if the second class had 30 students.

Ans .

Explanation :

If the ratio is 2 : 1 and the second class has 30 students, then the first class has 60 students

4 kg of rice at ` 5 per kg is mixed with 8 kg of rice at ` 6 per kg. Find the average price of the mixture.

6.66

5.66

3.66

1.66

Ans .

5.66

Explanation :

= (6 – Aw) : (Aw – 5)
fi(6 – Aw)/(Aw – 5) = 4/8 So 12 – 2 Aw = Aw – 5
Illustration 5
Thus 3 Aw = 17
We get  Aw = 5.66

5 kg of rice at ` 6 per kg is mixed with 4 kg of rice to get a mixture costing ` 7 per kg. Find the price of the costlier rice

8.75

5.25

8.25

6.25

Ans .

8.25

Explanation :

= (x – 7) : 1
(x – 7)/1 = 5/4 Æ 4x – 28 = 5
x =  8.25

On mixing two classes of students having average marks 25 and 40 respectively, the overall average obtained is 30 marks. Find the ratio in which the classes were mixed

5:1

3:1

2:1

4:1

Ans .

2:1

Explanation :

Hence, ratio is n1 = 40-30 and n2 = 30-25; ratio is 2 : 1, and the second class has 60 students

On mixing two classes of students having average marks 25 and 40 respectively, the overall average obtained is 30 marks. Find the the number of students in the first class if the second class had 30 students.

Ans .

Explanation :

Hence, ratio is n1 = 40-30 and n2 = 30-25; ratio is 2 : 1, and the second class has 60 students

4 kg of rice at ` 5 per kg is mixed with 8 kg of rice at ` 6 per kg. Find the average price of the mixture.

6.66

5.66

3.66

4.66

Ans .

5.66

Explanation :

n1=4, n2=8, A1 = 5, A2 = 6. So by solving we get the required answer is 5.66

A man buys 40 kg of rice at ` 20/kg and 60 kg of rice at ` 30/kg. Find his average price

Ans .

Explanation :

n1=40, n2=60, A1 = 20, A2 = 30. So by solving we get the required answer is 26

Pradeep mixes two mixtures of milk and water. He mixes 40 litres of the first containing 20% water and 60 litres of the second containing 30% water. Find the percentage of water in the final mixture.

Ans .

Explanation :

n1=40, n2=60, A1 = 20, A2 = 30. So by solving we get the required answer is 26

If 5 kg of salt costing ` 5/kg and 3 kg of salt costing ` 4/kg are mixed, find the average cost of the mixture per kilogram.

4.625

7.625

6.625

5.625

Ans .

4.625

Explanation :

n1=3, n2=5, A1 = 4, A2 = 5. So by solving we get the required answer 4.625/kg

Two types of oils having the rates of ` 4/kg and ` 5/kg respectively are mixed in order to produce a mixture having the rate of ` 4.60/kg. What should be the amount of the second type of oil if the amount of the first type of oil in the mixture is 40 kg?

Ans .

Explanation :

Mixing ` 4/kg and ` 5/kg to get ` 4.6 per kg we get that the ratio of mixing is 2:3. If the first oil is 40 kg, the second would be 60 kg

How many kilograms of sugar worth ` 3.60 per kg should be mixed with 8 kg of sugar worth ` 4.20 per kg, such that by selling the mixture at ` 4.40 per kg, there may be a gain of 10%?

Ans .

Explanation :

Since by selling at ` 4.40 we want a profit of 10%, it means that the average cost required is ` 4 per kg. Mixing sugar worth ` 3.6/kg and `4.2/kg to get ` 4/kg means a mixture ratio of 1:2. Thus, to 8 kg of the second variety we need to add 4 kg of the first variety to get the required cost price

A mixture of 125 gallons of wine and water contains 20% water. How much water must be added to the mixture in order to increase the percentage of water to 25% of the new mixture?

8.5

8.33

Ans .

 8.33

Explanation :

In 125 gallons we have 25 gallons water and 100 gallons wine. To increase the percentage of water to 25%, we need to reduce the percentage of wine to 75%. This means that 100 gallons of
wine = 75% of the new mixture. Thus the total mixture = 133.33 gallons. Thus, we need to mx
133.33 – 125 = 8.33 gallons of water in order to make the water equivalent to 25% of the mixture

400 students took a mock exam in Delhi. 60% of the boys and 80% of the girls cleared the cut off in the examination. If the total percentage of students qualifying is 65%, how many girls appeared in the examination?

300

200

100

Ans .

Explanation :

The ratio of boys and girls appearing for the exam can be seen to be 3:1 as A1 = 60, A2 = 80 and Aw=65

The average salary per head of all employees of a company is ` 600. The average salary of 120 officers is ` 4000. If the average salary per head of the rest of the employees is ` 560, find the total number of workers in the company.

10200

10320

10500

10680

Ans .

Explanation :

A1=560, A2=4000 and Aw=600 so solving we get it is clear that the ratio of the number of officers to the number of other employees
would be 40:3400. Since there are 120 officers, there would be 3400 × 3 = 10200 workers in the
company. Thus the total number of employees would be 10200 + 120 = 10320

In what ratio must rice at Rs. 9.30 per kg be mixed with rice at Rs. 10.80 per kg so that the mixture be worth Rs. 10 per kg

8 : 7

8 : 4

8 : 2

8 : 6

Ans .

Explanation :

Required ratio = 80 : 70 = 8 : 7. we get as A1 = 9.3 and Aw=10 and A2=10.8

How much water must be added to 60 litres of milk at 1 ½ litres for Rs. 20 So as to have a mixture worth Rs.10 2/3 a litre ?

Ans .

Explanation :

C.P. of 1 litre of milk = Rs. (20 x 2/3) = Rs. 40/3. The C.P of 1 liter of water is Rs. 0. So we have A1 = 0, Aw = 10 2/3 i.e. 32/3 and A2 = 40/3. We now have to find out n1/n2. So solving by alligation method we get Ratio of water and milk = 8/3 : 32/3  = 8 : 32 = 1 : 4
Quantity of water to be added to 60 litres of milk = [1/4 X 60 ]litres = 15 litre

In what ratio must water be mixed with milk to gain 20 % by selling the mixture at cost price ?

1 : 5

2 : 5

6 : 5

4 : 5

Ans .

1 : 5

Explanation :

Let C.P. of milk be Re. 1 per litre.
          Then, S.P. of 1 litre of mixture = Re. 1.  
         Gain obtained = 20%.
 C.P. of 1 litre of mixture = Rs.[(100/120)* 1] = Rs.5/6 
 By the rule of alligation, we have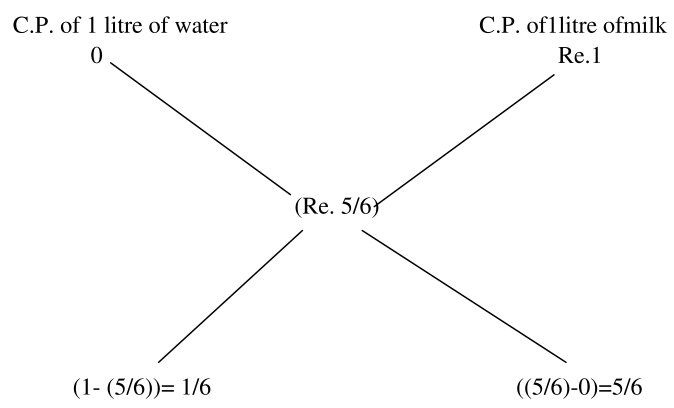 



Ratio of water and milk = 1/6 : 5/6 = 1 : 5

How many kgs. of wheat costing Rs. 8 per kg must be mixed with 36 kg of rice costing Rs. 5.40 per kg so that 20% gain may be obtained by Belling the mixture at Rs. 7.20 per kg ?

40.8

10.8

30.8

20.8

Ans .

10.8

Explanation :

S.P. of 1 kg mixture = Rs. 7.20,Gain = 20%.
     So C.P. of 1 kg mixture = Rs.[(100/120)*7.20]=Rs. 6. 
     By the rule of alligation, we have: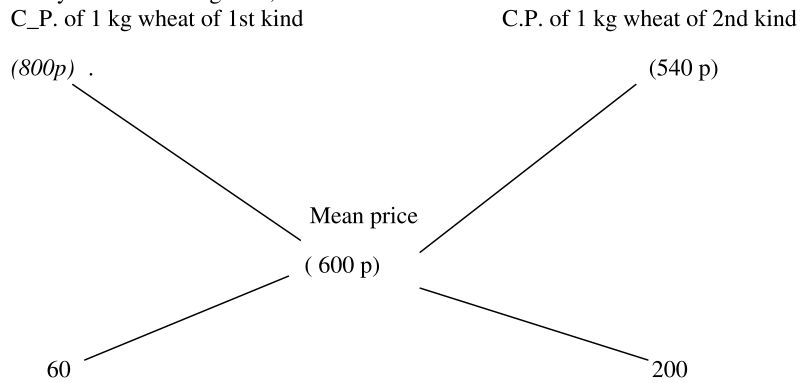



Let x kg of wheat of 1st kind be mixed with 36 kg of wheat of 2nd kind.
Then, 3 : 10 = x : 36 or lOx = 3 * 36 or x = 10.8 kg.

upscfever.com

Solved Question Papers

Solved Question Papers

UPSCFEVER - POPULAR PAGES

Join The Movement

Discussions and Comments