In the last section, you learned about the sliding windows object detection algorithm using a convnet but we saw that it was too slow.

In this section, you'll learn how to implement that algorithm convolutionally. Let's see what this means. To build up towards the convolutional implementation of sliding windows let's first see how you can turn fully connected layers in neural network into convolutional layers.

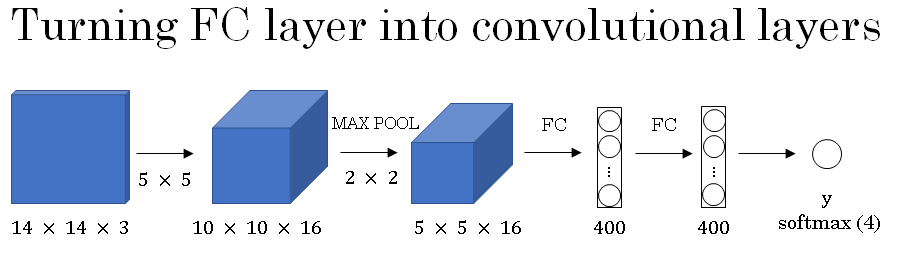
So let's say that your object detection algorithm inputs 14 by 14 by 3 images. This is quite small but just for illustrative purposes, and let's say it then uses 5 by 5 filters, and let's say it uses 16 of them to map it from 14 by 14 by 3 to 10 by 10 by 16. And then does a 2 by 2 max pooling to reduce it to 5 by 5 by 16. Then has a fully connected layer to connect to 400 units.

Then now they're fully connected layer and then finally outputs a Y using a softmax unit. This entire architecture is shown below.

The softmax unit Y as four numbers, corresponding to the class probabilities of the four classes that softmax units is classified amongst. And the four causes could be pedestrian, car, motorcycle, and background or something else.

Now, what I'd like to do is show how these layers can be turned into convolutional layers. So, the convnet will draw same as before for the first few layers.

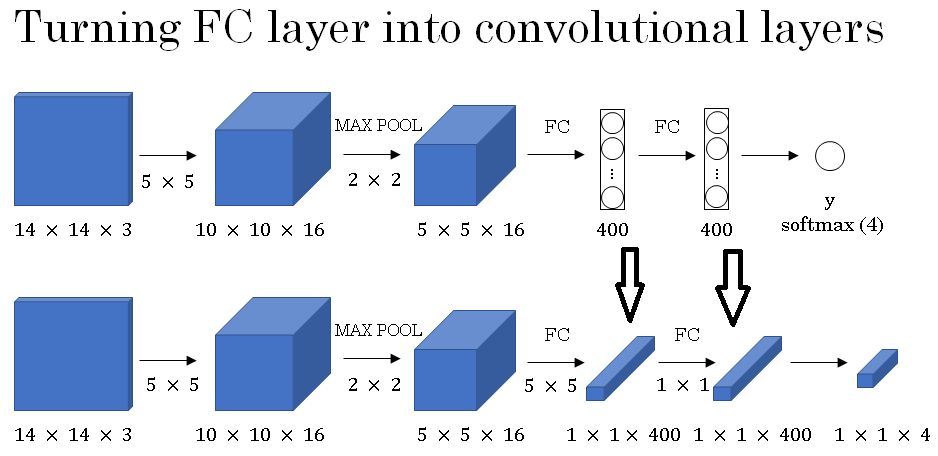
And now, one way of implementing this fully connected layer is to implement this as a 5 by 5 filter and let's use 400 - 5 by 5 filters.

So if you take a 5 by 5 by 16 image and convolve it with a 5 by 5 filter, remember, a 5 by 5 filter is implemented as 5 by 5 by 16 because our convention is that the filter looks across all 16 channels. So the 16 channel of the input image and the 16 channels of the filter must match and so the outputs will be 1 by 1.

And if you have 400 of these 5 by 5 by 16 filters, then the output dimension is going to be 1 by 1 by 400. So rather than viewing these 400 as just a set of nodes, we're going to view this as a 1 by 1 by 400 volume.

Mathematically, this is the same as a fully connected layer because each of these 400 nodes has a filter of dimension 5 by 5 by 16.

So each of those 400 values is some arbitrary linear function of these 5 by 5 by 16 activations from the previous layer.

Next, to implement the next convolutional layer, we're going to implement a 1 by 1 convolution.

If you have 400 - 1 by 1 filters then, with 400 filters the next layer will again be 1 by 1 by 400.

So that gives you this next fully connected layer. And then finally, we're going to implement a 1 by 1 convolution followed by a softmax activation.

So as to give a 1 by 1 by 4 volume to take the place of these four numbers that the network was operating.

So this shows how you can take these fully connected layers and implement them using convolutional layers so that the sets of fully connected units instead are implemented as 1 by 1 by 400 and 1 by 1 by 4 volumes.

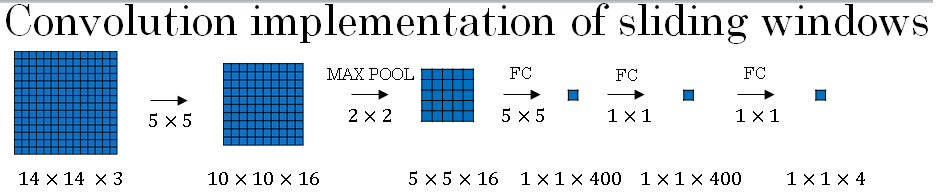
After this conversion, let's see how you can have a convolutional implementation of sliding windows object detection.

The architecture below is based on the OverFeat paper, referenced at the bottom, by Pierre Sermanet, David Eigen, Xiang Zhang, Michael Mathieu, Robert Fergus and Yann Lecun.

Here your sliding windows convnet inputs 14 by 14 by 3 images and again, I'm just using small numbers like the 14 by 14 image in this section mainly to make the numbers and illustrations simpler. So as before, you have a neural network as follows that eventually outputs a 1 by 1 by 4 volume, which is the output of your softmax (image shown above uses only the front face of the 3D images).

Now, this still has one weakness, which is the position of the bounding boxes is not going to be too accurate. In the next section, let's see how you can fix that problem.

In the architecture given below if the image input and the size of the sliding window are same then no sliding action is required and we can get the output predictions in one pass.

With convolutional implementation of sliding windows, we can get output in a single pass even if image and sliding window are of different sizes. This case is shown below:

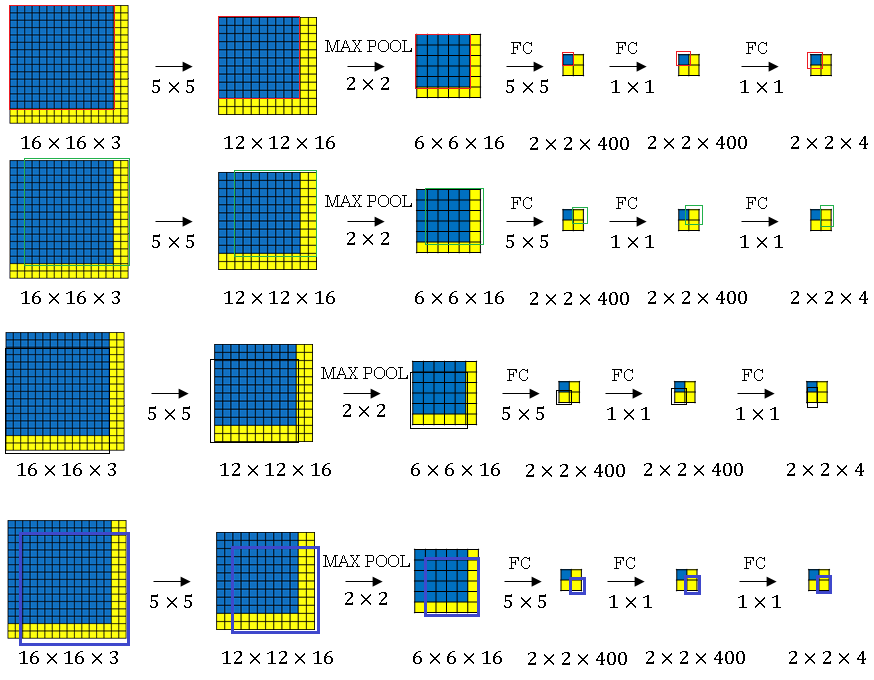
As shown in the above figure when a convolution implementation of sliding windows achive prediction of output in one pass.

The sliding window is passed for four times, the windows are shown in four colors above.

For each time we get a single output as 1 x 1 x 4 volume. All the four slides over the input image when concatenated give us a final 2 x 2 x 4 volume. Each 1 x 1 x 4 block of this volume corresponds to a particular sliding window over the image.

All four times can be done in a single pass over the input image.