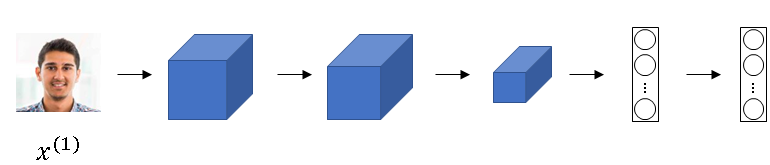
Siamese Network
The job of the function d, which you learned about in the last section, is to input two faces and tell you how similar or how different they are. A good way to do this is to use a Siamese network. Let's take a look.
You're used to seeing pictures of confidence like these where you input an image, let's say x1. And through a sequence of convolutional and pulling and fully connected layers, end up with a feature vector like that.
And sometimes this is fed to a softmax unit to make a classification. We're not going to use that in this section.
Instead, we're going to focus on the vector shown below which is of let's say 128 numbers computed by some fully connected layer that is deeper in the network.
And I'm going to give this list of 128 numbers a name. I'm going to call this \( f(x^{(1)}) \) (f of x(1)), and you should think of \( f(x^{(1)}) \) as an encoding of the input image x(1).
So it's taken the input image, here this picture of a person, and is re-representing it as a vector of 128 numbers. The way you can build a face recognition system is then that if you want to compare two pictures, let's say the first picture with a second picture as shown below.
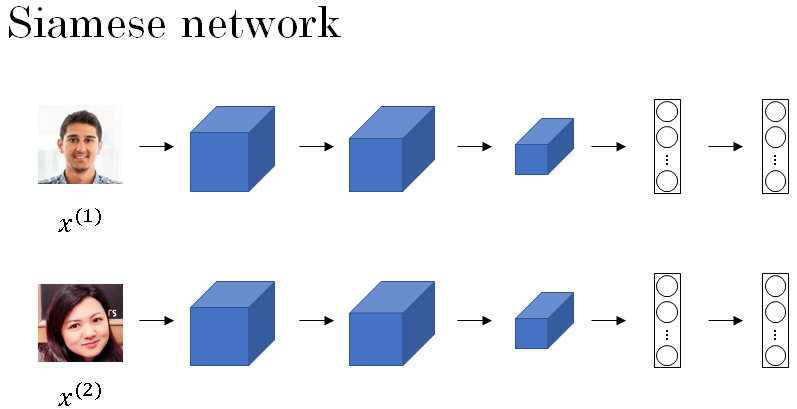
What you can do is feed this second picture to the same neural network with the same parameters and get a different vector of 128 numbers, which encodes this second picture.
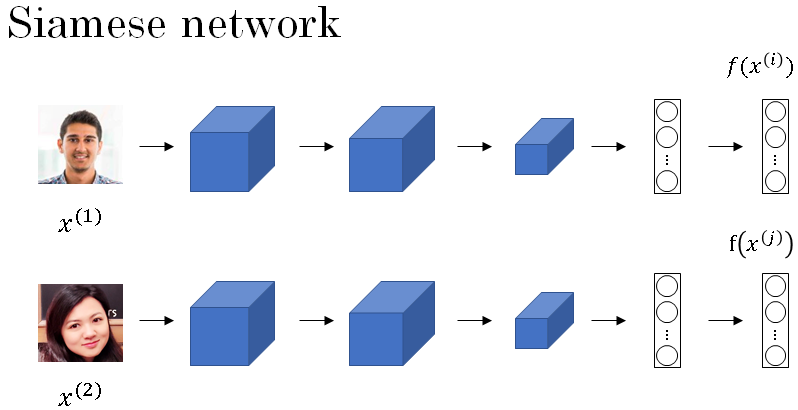
So I'm going to call this encoding of this second picture \( f(x^{(2)}) \), and here I'm using x(1) and x(2) just to denote two input images.
They don't necessarily have to be the first and second examples in your training sets. It can be any two pictures.
Finally, if you believe that these encodings are a good representation of these two images, what you can do is then define the image distance between x(1) and x(2) as the norm of the difference between the encodings of these two images.
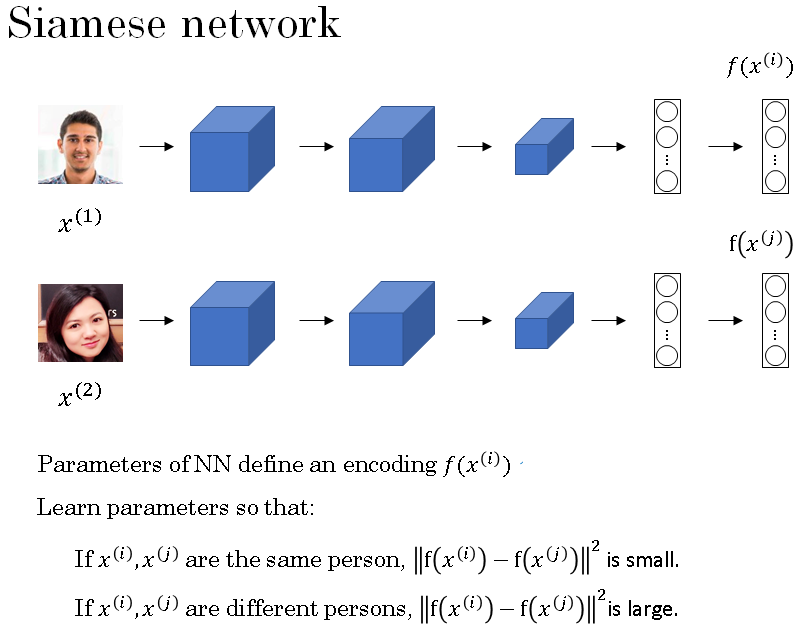
So this idea of running two identical, convolutional neural networks on two different inputs and then comparing them, sometimes that's called a Siamese neural network architecture.
And a lot of the ideas I'm presenting here came from this paper due to Yaniv Taigman, Ming Yang, Marc'Aurelio Ranzato, and Lior Wolf in the research system that they developed called DeepFace.
And many of the ideas I'm presenting here came from a paper due to Yaniv Taigman, Ming Yang, Marc'Aurelio Ranzato, and Lior Wolf in a system that they developed called DeepFace.
So how do you train this Siamese neural network? Remember that these two neural networks have the same parameters.
So what you want to do is really train the neural network so that the encoding that it computes results in a function d that tells you when two pictures are of the same person.
So more formally, the parameters of the neural network define an encoding \( f(x^{(i)}) \).
So given any input image x(i), the neural network outputs the 128 dimensional encoding \( f(x^{(i)}) \).
So more formally, what you want to do is learn parameters so that if two pictures, x(i) and x(j), are of the same person, then you want that distance between their encodings to be small.
And in the previous section, I was using x(1) and x(2), but it's really any pair x(i) and x(j) from your training set.
And in contrast, if x(i) and x(j) are of different persons, then you want that distance between their encodings to be large.
So as you vary the parameters in all of these layers of the neural network, you end up with different encodings.
And what you can do is use back propagation and vary all those parameters in order to make sure these conditions are satisfied.
So you've learned about the Siamese network architecture and have a sense of what you want the neural network to output for you in terms of what would make a good encoding.
But how do you actually define an objective function to make a neural network learn to do what we just discussed here? Let's see how you can do that in the next section using the triplet loss function.