You've seen how the convolution operation allows you to implement a vertical edge detector. In this section, you'll learn the difference between positive and negative edges, that is, the difference between light to dark versus dark to light edge transitions.

And you'll also see other types of edge detectors, as well as how to have an algorithm learn, rather than have us hand code an edge detector as we've been doing so far. So let's get started.

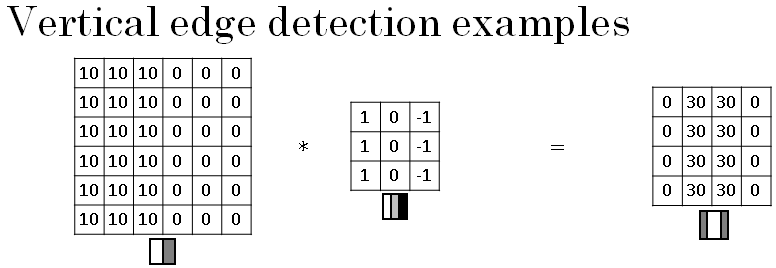
Below is the example you saw from the previous section, where you have an image, six by six, there's light on the left and dark on the right, and convolving it with the vertical edge detection filter results in detecting the vertical edge down the middle of the image.

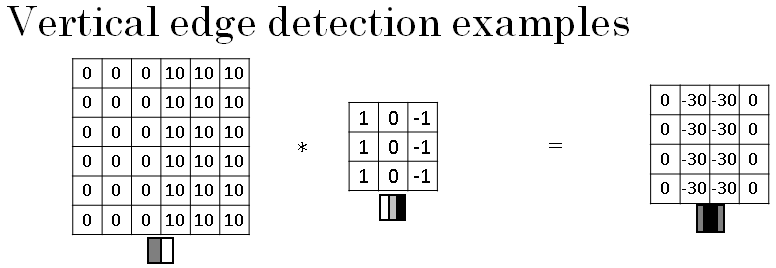
What happens in an image where the colors are flipped, where it is darker on the left and brighter on the right? So the 10s are now on the right half of the image and the 0s on the left. If you convolve it with the same edge detection filter, you end up with negative 30s, instead of 30 down the middle, and you can plot that as a picture thats shown below.

So because the shade of the transitions is reversed, the 30s now gets reversed as well. And the negative 30s shows that this is a dark to light rather than a light to dark transition.

And if you don't care which of these two cases it is, you could take absolute values of this output matrix. But this particular filter does make a difference between the light to dark versus the dark to light edges.

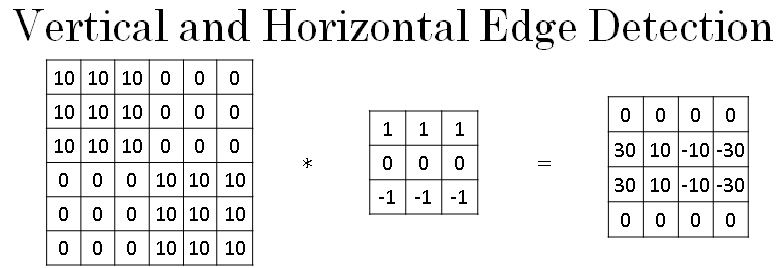
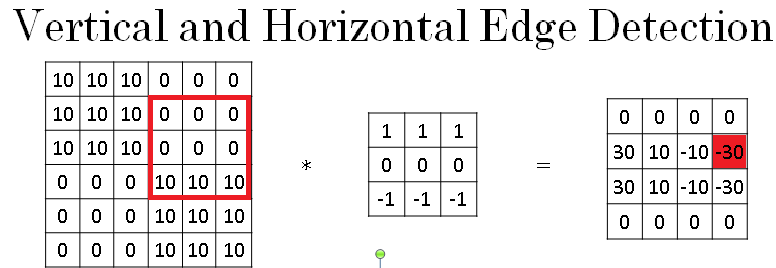
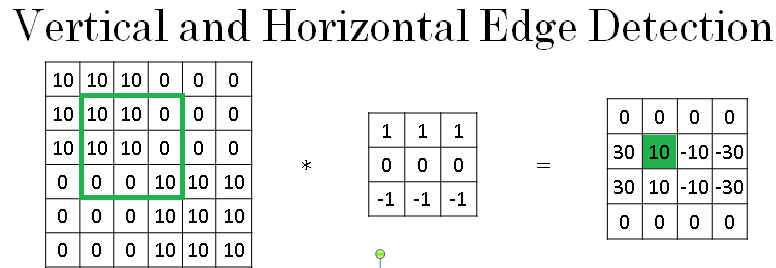
Let's see some more examples of edge detection. The three by three filter in image below given on the left we've seen allows you to detect vertical edges. Whereas the one on the right is a three by three filter to detect horizontal edges.

So as a reminder, a vertical edge according to this filter, is a three by three region where the pixels are relatively bright on the left part and relatively dark on the right part.

So similarly, a horizontal edge would be a three by three region where the pixels are relatively bright on top and relatively dark in the bottom row.

So given below is one example where you have here 10s in the upper left and lower right-hand corners. So if you draw this as an image, this would be an image which is going to be darker where there are 0s, so I'm going to shade in the darker regions, and then lighter in the upper left and lower right-hand corners. And if you convolve this with a horizontal edge detector, you end up as below.

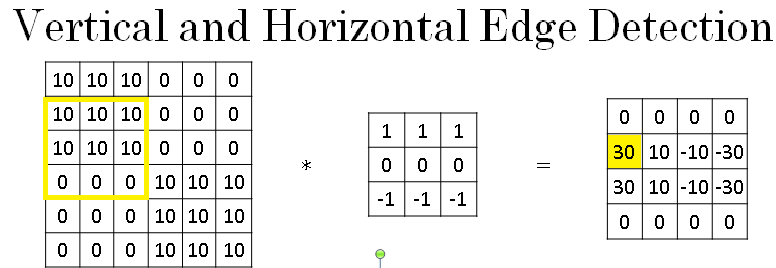
And so just to take a couple of examples, the 30 shown in yellow in below image corresponds to the three by three yellow region, where there are bright pixels on top and darker pixels on the bottom.

And so it finds a strong positive edge there.

And this -30 here corresponds to the red region, which is actually brighter on the bottom and darker on top. So that is a negative edge in this example.

Then the -10, for example, just reflects the fact that that filter captures part of the positive edge on the left and part of the negative edge on the right, and so blending those together gives you some intermediate value.

In large images, the intermediate values would be quite small relative to the size of the image. So in summary, different filters allow you to find vertical and horizontal edges.

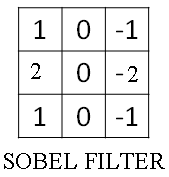
It turns out that the three by three vertical edge detection filter we've used is just one possible choice. And historically, in the computer vision literature, there was a fair amount of debate about what is the best set of numbers to use.

The image given below is called a Sobel filter. And the advantage of this is it puts a little bit more weight to the central row, the central pixel, and this makes it maybe a little bit more robust.

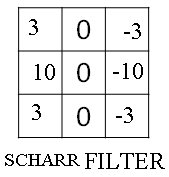
But computer vision researchers will use other sets of numbers too such as a Scharr filter. And this has yet other slightly different properties. And this is just for vertical edge detection. And if you flip it 90 degrees, you get horizontal edge detection.

And with the rise of deep learning, one of the things we learned is that when you really want to detect edges in some complicated image, maybe you don't need to have computer vision researchers handpick these nine numbers.

Maybe you can just learn them and treat the nine numbers of this matrix as parameters, which you can then learn using back propagation. And the goal is to learn nine parameters so that when you take the image, the six by six image, and convolve it with your three by three filter, that this gives you a good edge detector.

And what you see in later sections is that by just treating these nine numbers as parameters, the backprop can choose to learn 1, 1, 1, 0, 0, 0, -1,-1, if it wants, or learn the Sobel filter or learn the Scharr filter, or more likely learn something else that's even better at capturing the statistics of your data than any of these hand coded filters.

And rather than just vertical and horizontal edges, maybe it can learn to detect edges that are at 45 degrees or 70 degrees or 73 degrees or at whatever orientation it chooses

. And so by just letting all of these numbers be parameters and learning them automatically from data, we find that neural networks can actually learn low level features, can learn features such as edges, even more robustly than computer vision researchers are generally able to code up these things by hand.

But underlying all these computations is still this convolution operation, Which allows back propagation to learn whatever three by three filter it wants and then to apply it throughout the entire image, at this position, at this position, at this position, in order to output whatever feature it's trying to detect.

Be it vertical edges, horizontal edges, or edges at some other angle or even some other filter that we might not even have a name for in English.

So the idea you can treat these nine numbers as parameters to be learned has been one of the most powerful ideas in computer vision. And later in this course, we'll actually talk about the details of how you actually go about using back propagation to learn these nine numbers.

But first, let's talk about some other details, some other variations, on the basic convolution operation. In the next sections, I want to discuss with you how to use padding as well as different strides for convolutions.

And these two will become important pieces of this convolutional building block of convolutional neural networks. So let's go on to the next section.