Strided convolutions is another piece of the basic building block of convolutions as used in Convolutional Neural Networks.

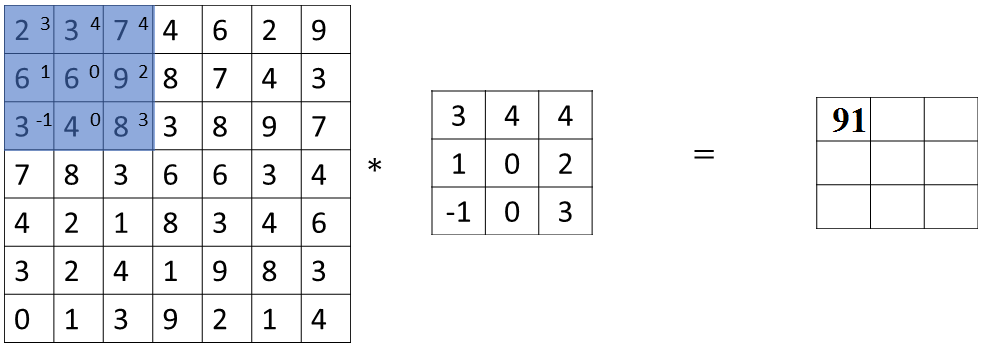
Let me show you an example. Let's say you want to convolve this seven by seven image with this three by three filter, except that instead of doing the usual way, we are going to do it with a stride of two.

What that means is you take the element wise product as usual in this upper left three by three region and then multiply and add and that gives you 91.

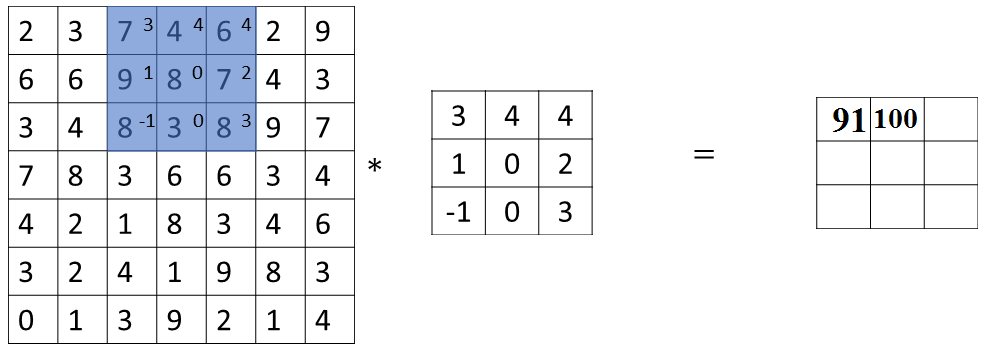
But then instead of stepping the blue box over by one step, we are going to step over by two steps. So, we are going to make it hop over two steps like so. Notice how the upper left hand corner has gone to new start, jumping over one position.

And then you do the usual element wise product and summing it turns out 100.

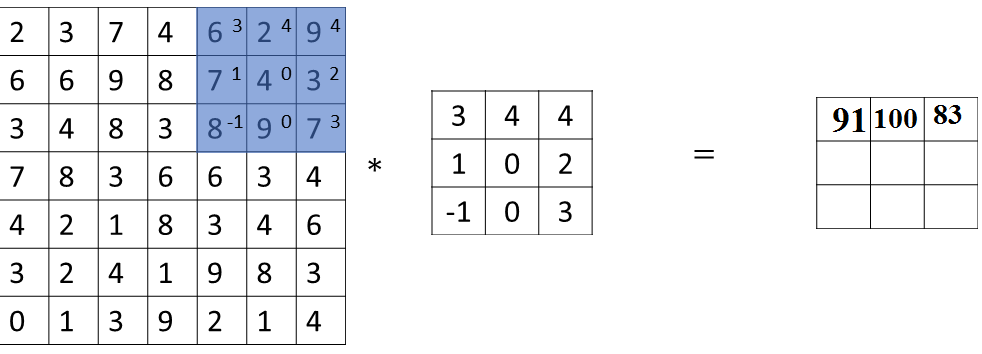
And now we are going to do they do that again, and make the blue box jump over by two steps. You end up at new position, and that gives you 83.

Now, when you go to the next row, you again actually take two steps instead of one step so going to move the blue box.

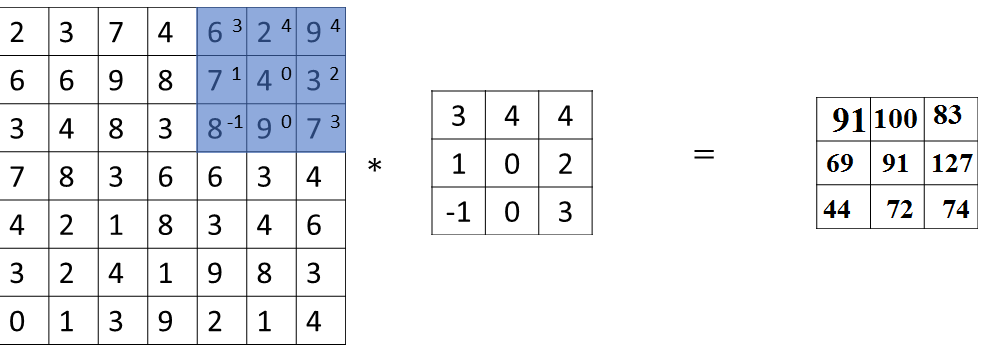
Notice how we are stepping over one of the positions and then this gives you 69, and now you again step over two steps, this gives you 91 and so on so 127. And then for the final row 44, 72, and 74.

In this example, we convolve with a seven by seven matrix to this three by three matrix and we get a three by three outputs.

The input and output dimensions turns out to be governed by the following formula, if you have an N by N image, they convolve with an F by F filter. And if you use padding P and stride S.

In this example, S is equal to two then you end up with an output that is N plus two P minus F, and now because you're stepping S steps of the time, you get \( \frac{n + 2p - f}{s} + 1 x \frac{n + 2p - f}{s} + 1 \)

In our example, we have seven plus zero, minus three, divided by two S stride plus one equals let's see, that's four over two plus one equals three, which is why we wound up with this is three by three output.

Now, just one last detail which is what of this fraction is not an integer? In that case, we're going to round this down \( \left \lfloor \frac{n + 2p - f}{s} + 1 \right \rfloor , \left \lfloor \frac{n + 2p - f}{s} + 1 \right \rfloor \) so this notation denotes the flow of something.

It means taking Z and rounding down to the nearest integer.

The way this is implemented is that you take this type of blue box multiplication only if the blue box is fully contained within the image or the image plus to the padding and if any of this blue box kind of part of it hangs outside and you just do not do that computation.

Then it turns out that if that's the convention that your three by three filter, must lie entirely within your image or the image plus the padding region before there's as a corresponding output generated that's convention.

Then the right thing to do to compute the output dimension is to round down in case this N plus two P minus F over S is not an integer. Just to summarize the dimensions, if you have an N by N matrix or N by N image that you convolve with an F by F matrix or F by F filter with padding P and stride S, then the output size will have \( \left \lfloor \frac{n + 2p - f}{s} + 1 \right \rfloor , \left \lfloor \frac{n + 2p - f}{s} + 1 \right \rfloor \) dimension.

It is nice we can choose all of these numbers so that there is an integer although sometimes you don't have to do that and rounding down is just fine as well.

But please feel free to work through a few examples of values of N, F, P and S on yourself to convince yourself if you want, that this formula is correct for the output size.

In the next section, you'll see how to carry out convolutions over volumes and this would make what you can do a convolutions sounds really much more powerful.