The different versions of RNNs you've seen so far will already work quite well by themselves.

But for learning very complex functions sometimes is useful to stack multiple layers of RNNs together to build even deeper versions of these models.

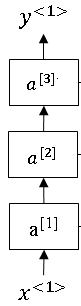
In this section, you'll see how to build these deeper RNNs. Let's take a look. So you remember for a standard neural network, you will have an input X.

And then that's stacked to some hidden layer and so that might have activations of say, \(a^{[1]}\) for the first hidden layer, and then that's stacked to the next layer with activations \(a^{[2]}\) , then maybe another layer, activations \(a^{[3]}\) and then you make a prediction \( \hat{y} \).

So a deep RNN is a bit like this, by taking this network and unrolling that in time.

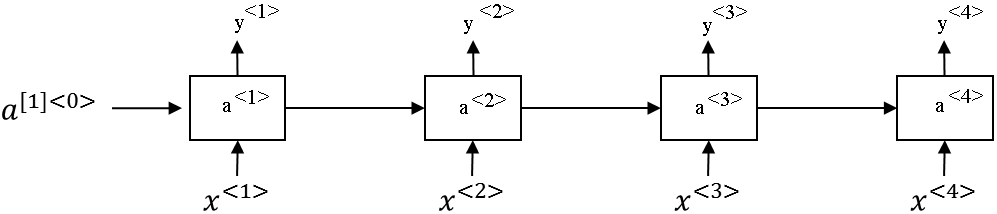
So let's take a look. So here's the standard RNN that you've seen so far.

But I've changed the notation a little bit which is that, instead of writing this as \(a^{[1]<0>}\) for the activation time zero, I've added this square bracket 1 to denote that this is for layer one.

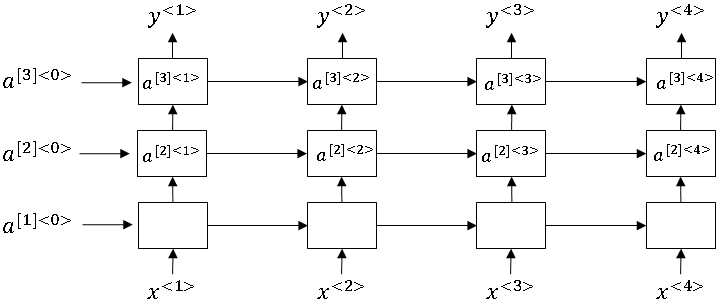
So the notation we're going to use is \(a^{[1]}\) to denote that it's an activation associated with layer 1 and then to denote that that's associated over time t.

So this will have an activation on \(a^{[1]<1>}\), this would be \(a^{[1]<2>}, a^{[1]<3>}, a^{[1]<4>}\). And then we can just stack these things on top and so this will be a new network with three hidden layers. So let's look at an example of how this value is computed.

So \( a^{[2]<3>} \) has two inputs. It has the input coming from the bottom, and there's the input coming from the left. So the computer has an activation function g applied to a way matrix. This is going to be Wa because computing an a quantity, an activation quantity.

And for the second layer, and so I'm going to give this \( a^{[2]<2>}\), there's that thing, comma \( a^{[1]<3>} \), there's that thing, plus ba associated to the second layer. And that's how you get that activation value. And so the same parameters \( {W_a}^{[2]} , {b_a}^{[2]} \) are used for every one of these computations at this layer. Whereas, in contrast, the first layer would have its own parameters \( {W_a}^{[1]} , {b_a}^{[1]} \).

So whereas for standard RNNs like the one on the left, you know we've seen neural networks that are very, very deep, maybe over 100 layers. For RNNs, having three layers is already quite a lot. Because of the temporal dimension, these networks can already get quite big even if you have just a small handful of layers.

And you don't usually see these stacked up to be like 100 layers. One thing you do see sometimes is that you have recurrent layers that are stacked on top of each other. But then you might take the output here, let's get rid of this, and then just have a bunch of deep layers that are not connected horizontally but have a deep network here that then finally predicts y<1>.

And you can have the same deep network here that predicts \(y^{<2>}\). So this is a type of network architecture that we're seeing a little bit more where you have three recurrent units that connected in time, followed by a network, followed by a network after that, as we seen for \(y^{<3>}\) and \(y^{<4>}\), of course.

There's a deep network, but that does not have the horizontal connections. So that's one type of architecture we seem to be seeing more of. And quite often, these blocks don't just have to be standard RNN, the simple RNN model.

They can also be GRU blocks LSTM blocks. And finally, you can also build deep versions of the bidirectional RNN. Because deep RNNs are quite computationally expensive to train, there's often a large temporal extent already, though you just don't see as many deep recurrent layers.

This has, I guess, three deep recurrent layers that are connected in time. You don't see as many deep recurrent layers as you would see in a number of layers in a deep conventional neural network. So that's it for deep RNNs.

With what you've seen this week, ranging from the basic RNN, the basic recurrent unit, to the GRU, to the LSTM, to the bidirectional RNN, to the deep versions of this that you just saw, you now have a very rich toolbox for constructing very powerful models for learning sequence models.