Let's start to formalize the problem of learning a good word embedding.

When you implement an algorithm to learn a word embedding, what you end up learning is an embedding matrix.

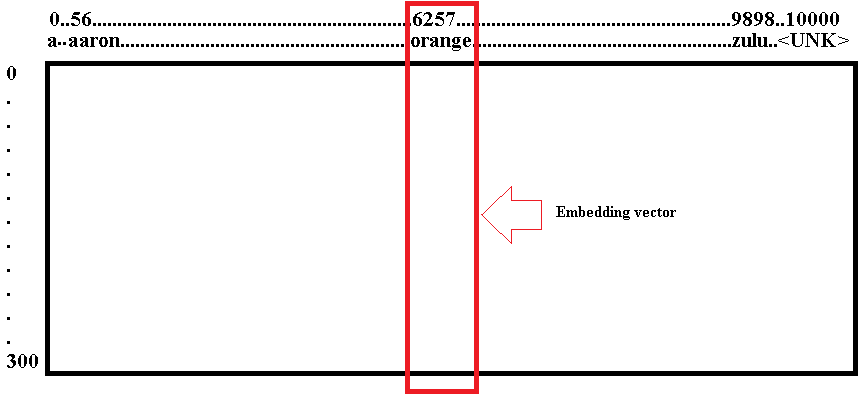
Let's take a look at what that means. Let's say, as usual we're using our 10,000-word vocabulary as shown below [from 'a' to ''].

So, the vocabulary has A, Aaron, Orange, Zulu, maybe also unknown word as a token.

What we're going to do is learn embedding matrix E, which is going to be a 300 dimensional by 10,000 dimensional matrix, if you have 10,000 words vocabulary.

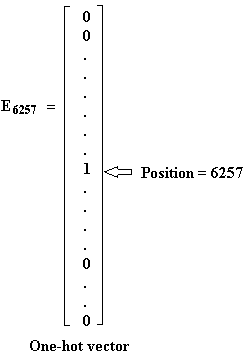
And the columns of this matrix would be the different embeddings for the 10,000 different words you have in your vocabulary. So, Orange was word number 6257 in our vocabulary of 10,000 words. So, one piece of notation we'll use is that E₆₂₅₇ was the one-hot vector with zeros everywhere and a one in position 6257.

And so, this will be a 10,000-dimensional vector with a one in just one position. So, this isn't quite a drawn scale. Yes, this should be as tall as the embedding matrix on the left is wide.

And if the embedding matrix is called capital E then notice that if you take E and multiply it by just one-hot vector by E₆₂₅₇, then this will be a 300-dimensional vector. So, E is 300 by 10,000 and E₆₂₅₇ is 10,000 by 1.

So, the product will be 300 by 1. The embedding matrix E times this one-hot vector E₆₂₅₇ winds up selecting out the 300-dimensional column corresponding to the word Orange.

So, this is going to be equal to E₆₂₅₇ which is the notation we're going to use to represent the embedding vector that 300 by one dimensional vector for the word Orange. And more generally, E for a specific word W, this is going to be embedding for a word W.

So, the thing to remember from this section is that our goal will be to learn an embedding matrix E and what you see in the next section is you initialize E randomly and you're straight in the sense to learn all the parameters of this 300 by 10,000 dimensional matrix and E times this one-hot vector gives you the embedding vector.

Now just one note, theoretically you take the matrix E and multiply it by the one-hot vector O.

But if when you're implementing this, it is not efficient to actually implement this as a mass matrix vector multiplication because the one-hot vectors, now this is a relatively high dimensional vector and most of these elements are zero.

So, it's actually not efficient to use a matrix vector multiplication to implement this because if we multiply a whole bunch of things by zeros and so the practice, you would actually use a specialized function to just look up a column of the Matrix E rather than do this with the matrix multiplication. But writing of the map, it is just convenient to write it out this way.

So, in Case for example there is a embedding layer and we use the embedding layer then it more efficiently just pulls out the column you want from the embedding matrix rather than does it with a much slower matrix vector multiplication.

So, in this section you saw the notations were used to describe algorithms to learning these embeddings and the key terminology is this matrix capital E which contain all the embeddings for the words of the vocabulary. In the next section, we'll start to talk about specific algorithms for learning this matrix E.