Part of Speech Tagging and Hidden Markov Models - Introduction
Part of speech refers to the category of words or the lexical terms in a language.
Examples of these lexical terms in the English language would be noun, verb, adjective, adverb, pronoun, preposition although there are many others.
Let's take a look at this sentence.
Writing out the names of these terms can quickly become cumbersome during text analysis.
You're going to use a short representation called tags to represent these categories. The process of assigning these tags to the words of a sentence or your corpus is referred to as parts of speech tagging or POS, tagging for shorts.
Because POS tags describe the characteristic structure of lexical terms in a sentence or text, you can use them to make assumptions about semantics.
They're used for identifying named entities too.
In a sentence such as the Eiffel Tower is located in Paris, Eiffel Tower and Paris are both named entities.
Tags are also used for coreference resolution. If you have the two sentences, the Eiffel Tower is located in Paris, it is 324 meters high, you can use part-of-speech tagging to infer that ``it'' refers in this context to the Eiffel Tower.
Another application is speech recognition, where you use parts of speech tags to check if a sequence of words has a high probability or not.
You now know the different applications of parts of speech tagging.


Markov chains
Markov chains are really important because they are used in speech recognition. And they're also used for parts of speech tagging.
Before jumping in let's start with a small example, to show what you want to accomplish. And then you will see how Markov chains can help accomplish the task.
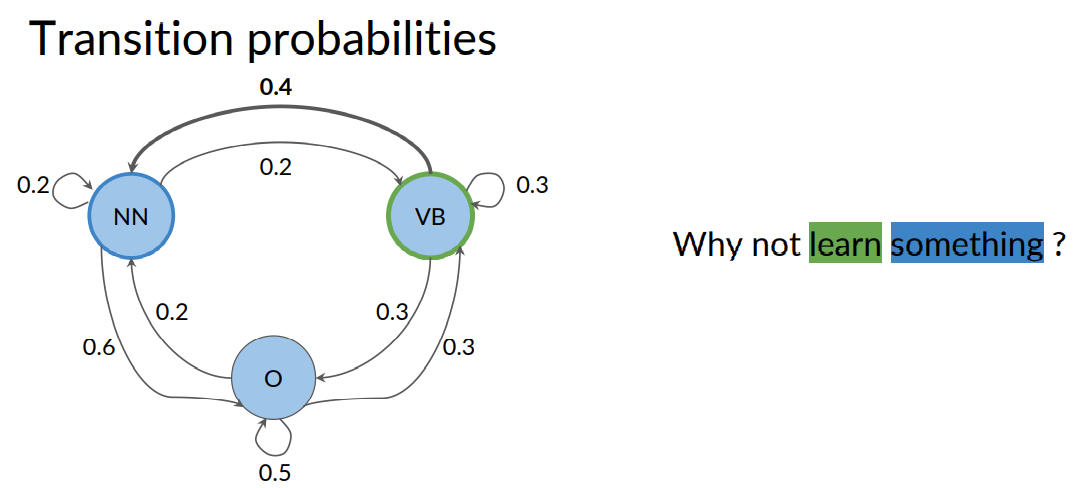
If you look at the sentence, why not learn, the word learn is a verb.
The question you want to answer is whether the following word in the sentence is a noun, a verb, or some other parts of speech.
If you're familiar with the English language, you might guess that if you see a verb in the sentence, the following word is more likely to be a noun.
Rather than another verb.
So the idea here, is that the likelihood of the next words part of speech tag in a sentence tends to depend on the part of speech tag of the previous word. Makes sense, right?
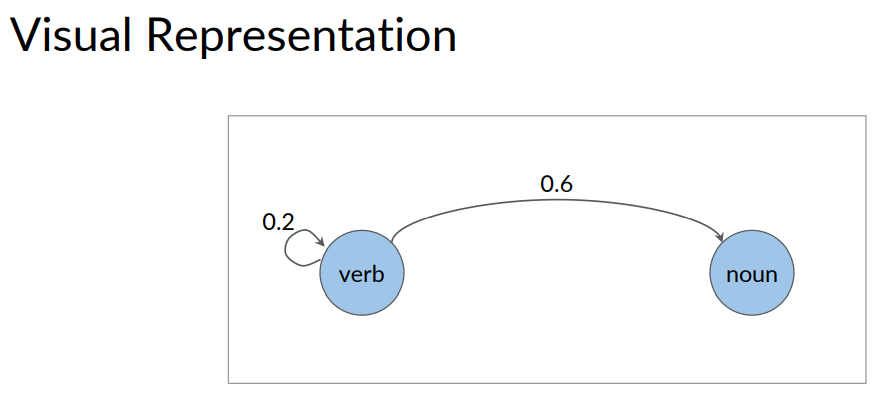
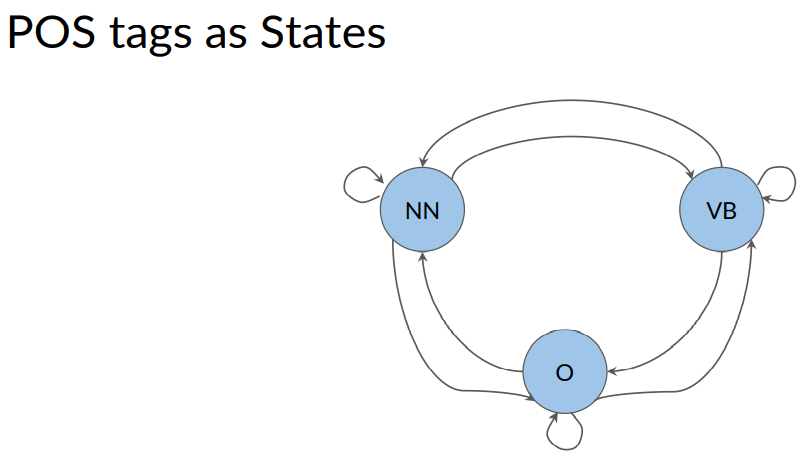
You can represent a different likelihoods visually.
Here you have a circle representing a verb.
And over here you have a circle representing a noun.
You can draw an arrow that goes from the verb circle to the noun circle.
So the following arrow. You can draw another arrow that goes from the verb circle, and loops around back to point at itself.
You can associate numbers with each of these arrows. Where a larger number means that there is a higher likelihood, you're moving from one circle to the other.
In this example, the arrow that goes from the verb so the noun maybe 0.6. Whereas the arrow that goes from the verb, back to the verb has a 0.2. The higher number of 0.6, means that it's more likely to go from a verb to a noun. As opposed to from a verb, to another verb. This is a great example of how Markov chains work on a very small scale.
So what's our Markov chains?
They're a type of stochastic model that describes a sequence of possible events.
To get the probability for each event, it needs only the states of the previous events.
The word stochastic just means random or randomness. So a stochastic model, incorporates and models processes does have a random component to them.
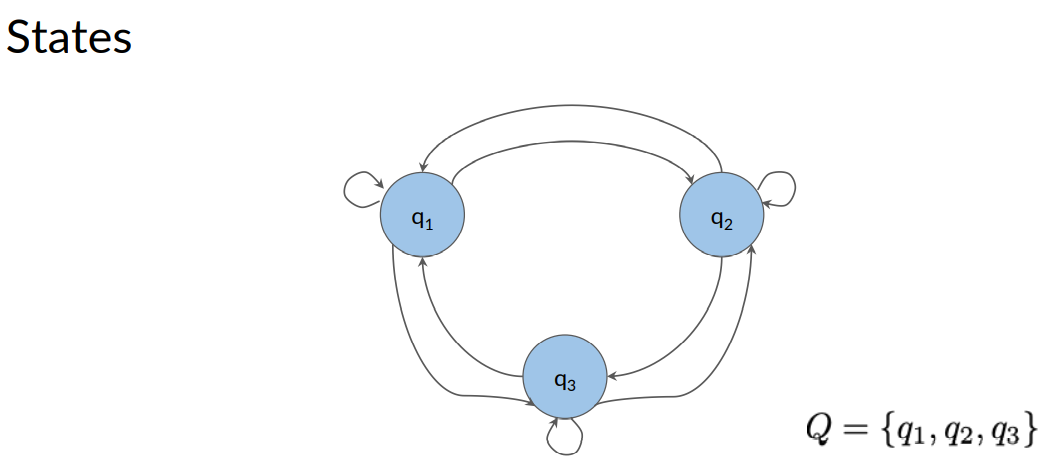
A Markov chain, can be depicted as a directed graph. So in the context of Computer Science, a graph is a kind of data structure that is visually represented, as a set of circles connected by lines.
When the lines that connect the circles have arrows that indicates a certain direction, this is called a directed graph. The circles of the graph, represents states of our model.
A state refers to a certain condition of the present moment. For example, if you are using a graph to model whether water is in a frozen state, a liquid state, or a gas state.
Then you would draw a circle, for each of these states to represent the three possible states that water can be at the present moment.
I'm labeling each state as q1, q2, q3 etc. To give them each a unique name. Then referring to the set of all states with a capital letter Q. For this graph there are three states, q1, q2, and q3.
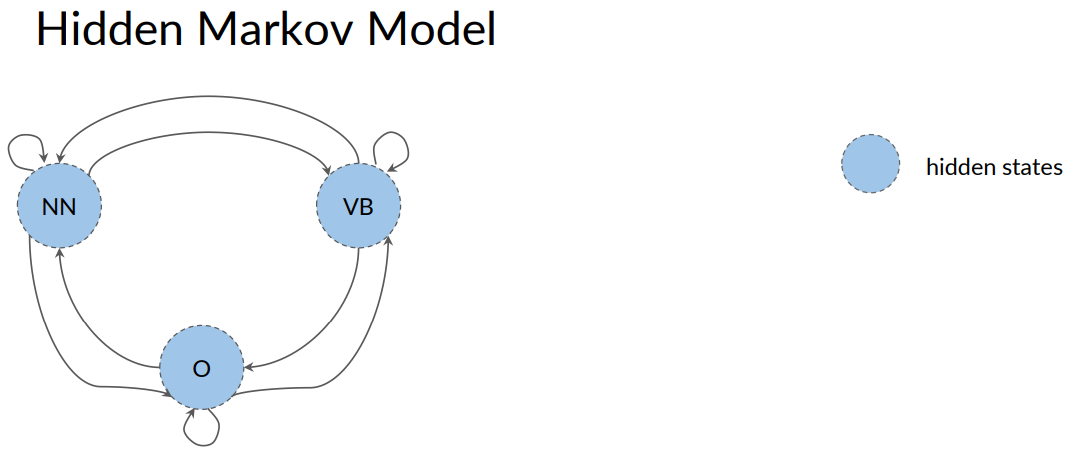
You now learned about the states in your model. And we said that the states represent the condition, or the present moments. These states, could be thought of as part of speech tags. Maybe one states could correspond to the verbs. Another one could correspond to the nouns and so forth.

Markov Chains and POS Tags
If you think about a sentence as a sequence of words with associated part of speech tags. You can represent that sequence with a graph.
Where the parts of speech tags are events that can occur. Depicted by the state of our model graph.
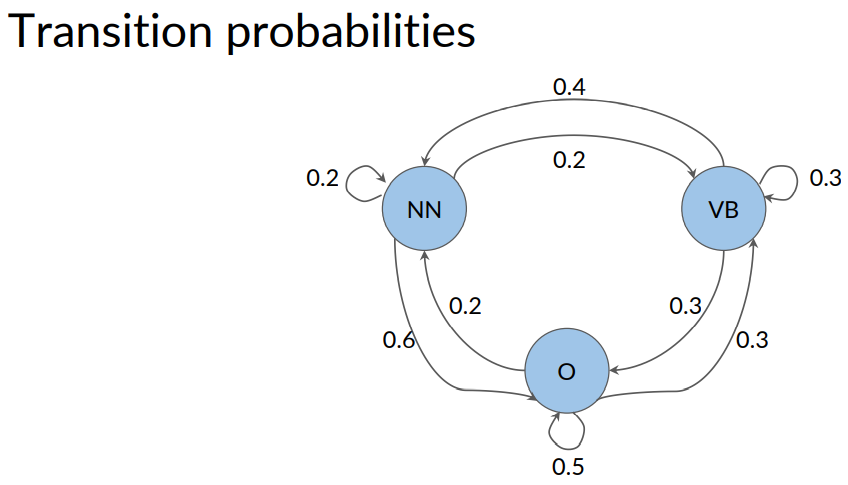
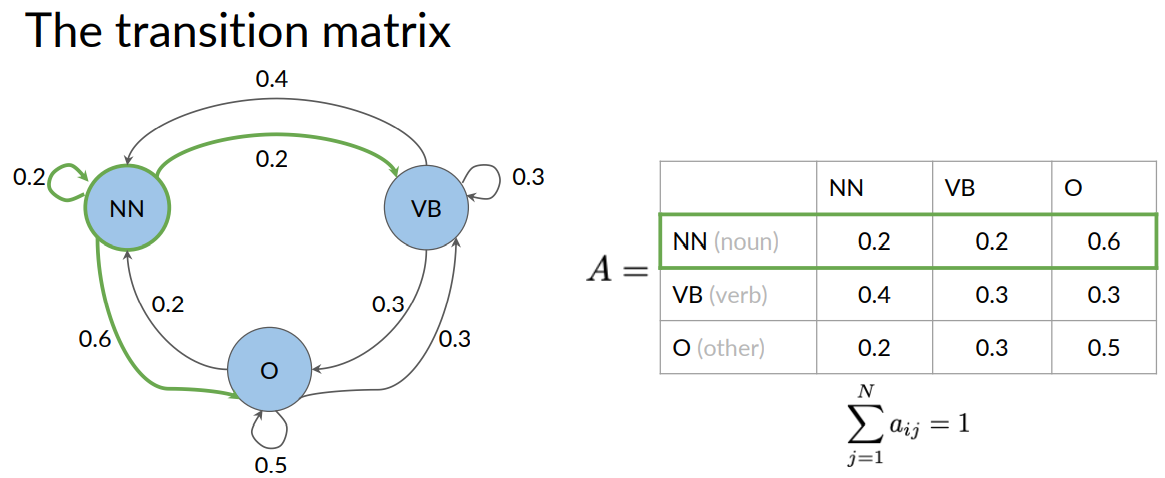
In this example, NN is for noun , VB is for verbs. And other, stands for all other tags.
The edges of the graph have weights or transition probabilities associated with them. Which defined the probability of going from one state to another.
There is one less important property that's Markov chains possess. The so called Markov property.
Which states that the probability of the next event only depends on the current event. The Markov property helps keep the model simple. By saying, all you need to determine the next state is the current states. It doesn't need information from any of the previous states.
Going back to the analogy whether water is in solid, liquid or gas states. If you look at a cup of water that is sitting outside. The current state of the water is a liquid states.
When modeling the probability that the water in the cup will transition into the gas states. You don't need to know the previous history of the water. Whether it's previously came from ice cubes. Or whether it's previously came from rain clouds. That makes sense, right.
Let's revisit the sentence example from earlier. If you look at this sentence again and want to know the probability that the next word. Following learn is a noun. Then this just depends on the current state that you're in.
In this case, the verb states denoted by VB.
Because the current word learn is a verb. So, the probability of the next word being a noun. Is the transition probability for going from the verb to the noun and N states.
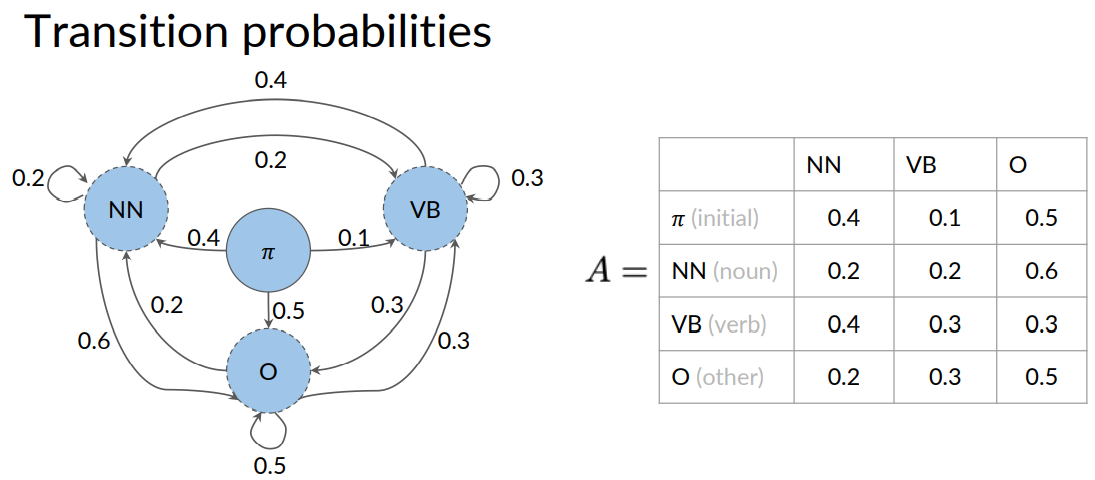
The transition probability is written on the arrow that goes from VB to NN. And as you can see, it's 0.4.
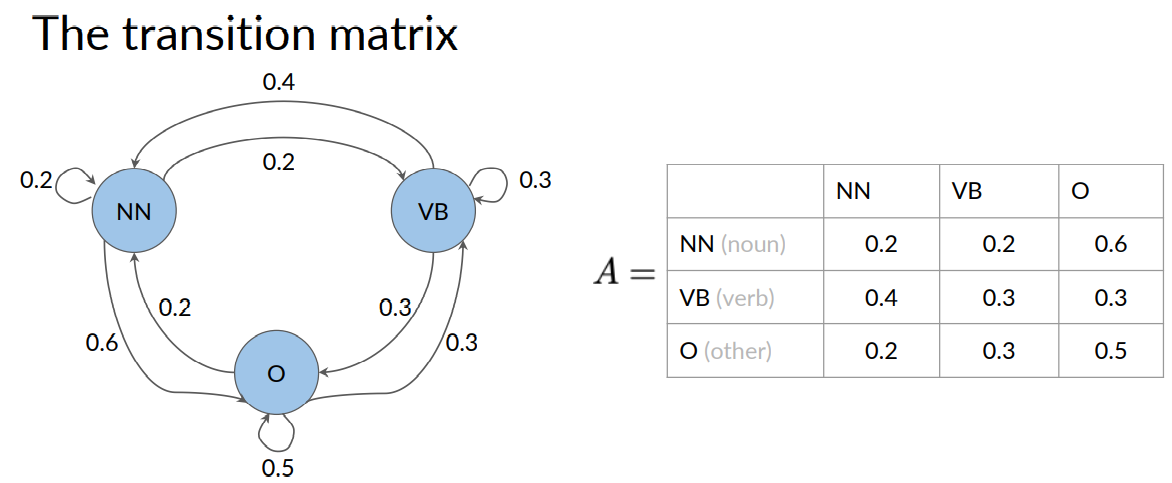
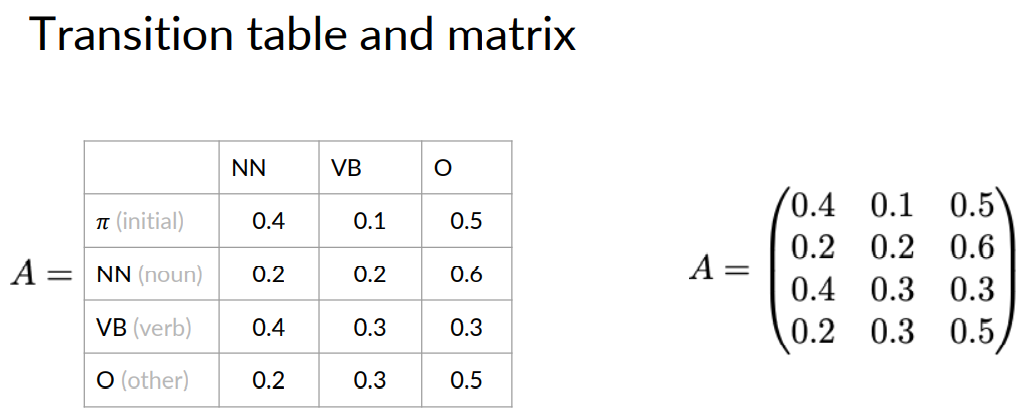
You can also use a table to store the states and transition probabilities.
A table is an equivalent but more compact representation of the Markov chain model. And this table is called a transition matrix. A transition matrix is an N by N matrix, with N being the number of states in the graph.
Each role in the matrix represents transition probabilities of one states to all other states. For example, the first row represents the case where the current state is a noun . The columns represent the possible future states that might come next.
The values inside the table represent the transition probability of going from a noun to a noun. From a noun to a verb and then a noun to some other states.
Notice that for all the outgoing transition probabilities from a given state. These some of these transition probabilities should always be one.
Equivalently in the transition matrix. All of the transition probabilities in each row should add up to one.
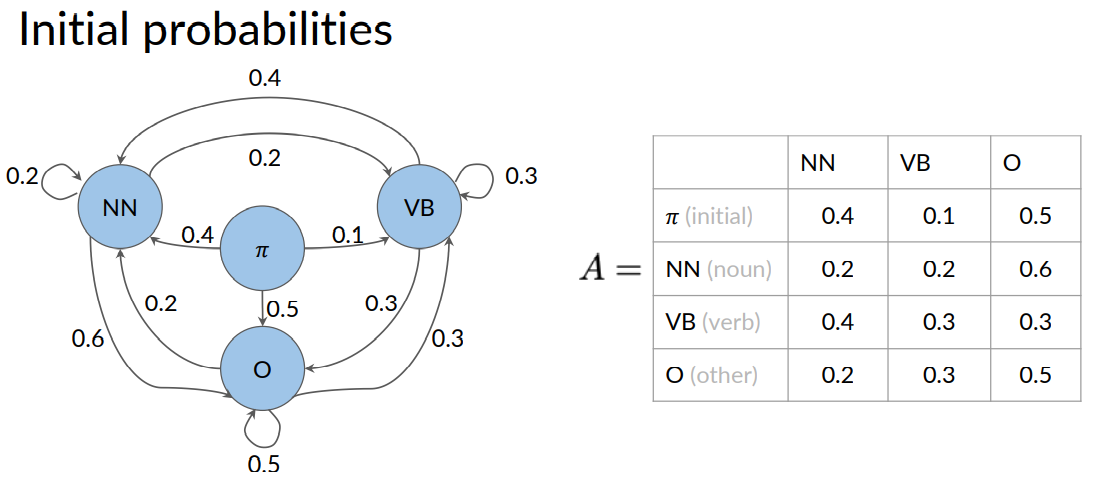
Some of you may have noted one little flaw in this model. It doesn't tell you how to assign a part of speech tag to the first word in the sentence.
This is because all of the states and the model corresponds to words.
But what do you do when there is no previous word? As in the case, when beginning a sentence. To handle this, you can introduce what is known as an initial state.
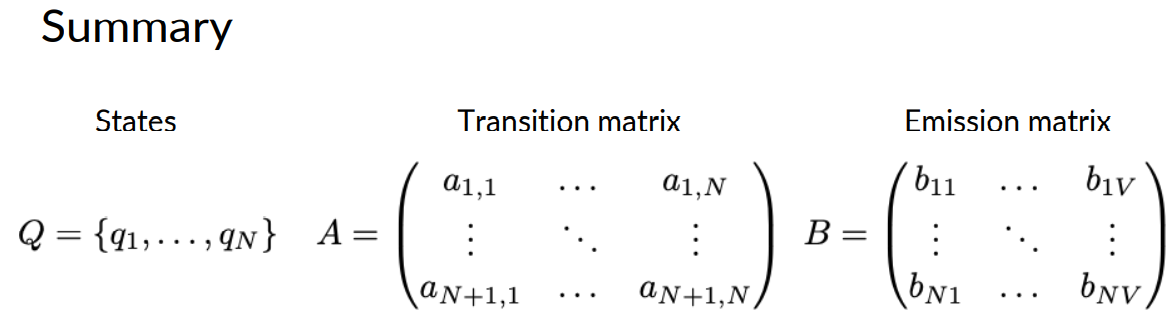
By, you include these probabilities in the table A. So now, it has dimensions and plus one by N. Notice that the transition matrix can be written as an actual matrix like this.
To recap, Markov chains consists of a set queue of N states. Q1 all the way to QN. The transition matrix A has the dimensions N plus 1 by N. With the initial probabilities in the first row.
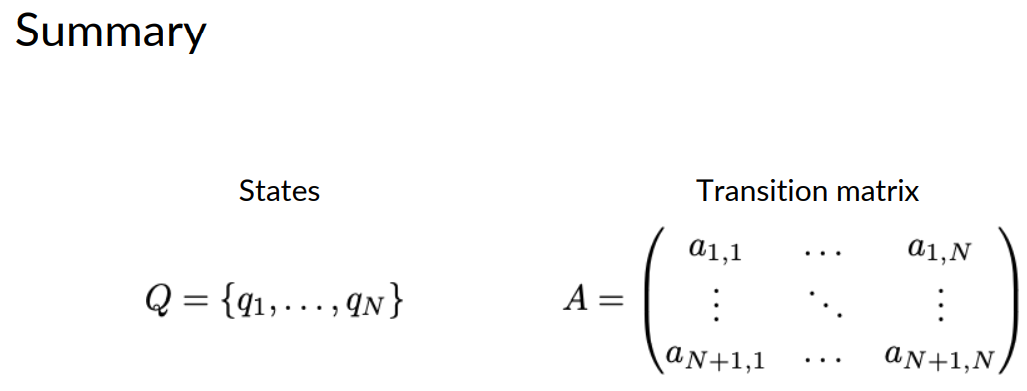
Hidden Markov Models
The name Hidden Markov model implies that states are hidden or not directly observable.
Going back to the Markov model that has the states for the parts of speech, such as noun, verb, or other, you can now think of these as hidden states because these are not directly observable from the text data.
It may seem a little confusing to think that this data is hidden.
Because if you look at a certain word such as jump, as a human who is familiar with the English language, you can see that this is a verb.
From a machine's perspective, however, it only sees the text jump and doesn't know whether it is a verb or a noun.
For a machine looking at the text data, what it's going to observe are the actual words such as jump, run, and fly. These words are said to be observable because they can be seen by the machine.
The Markov chain model and Hidden Markov model have transition probabilities, which can be represented by a matrix A of dimensions N plus 1 by N, where N is the number of hidden states.
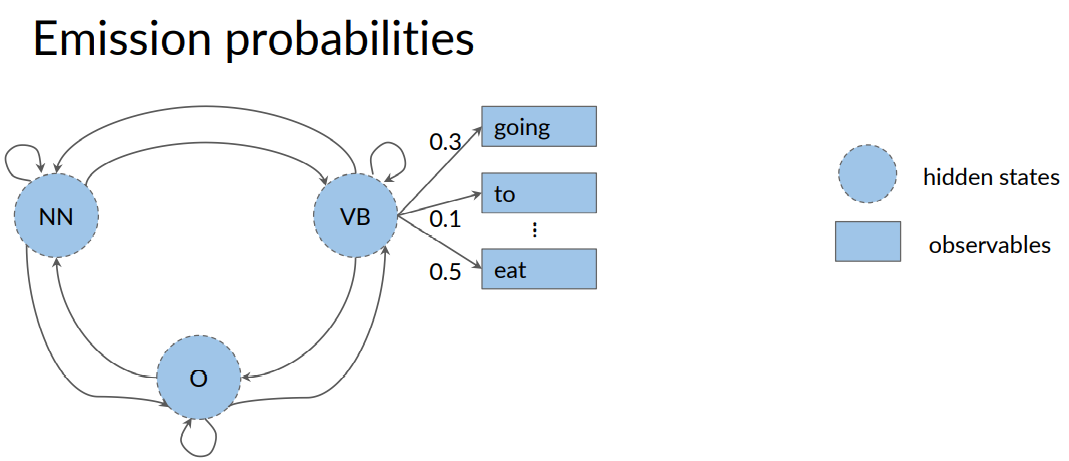
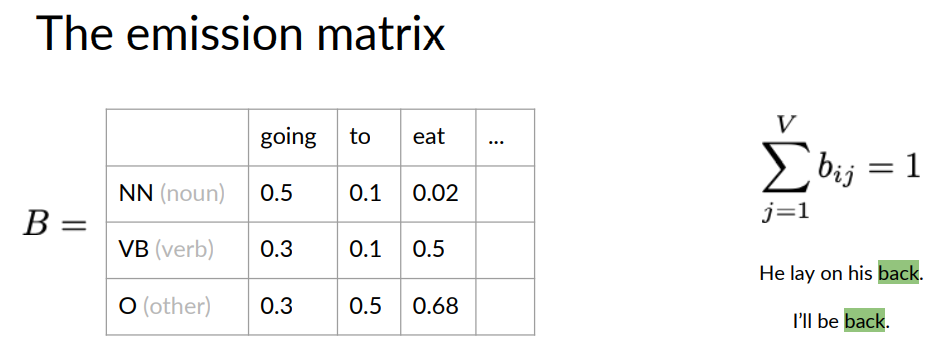
The Hidden Markov model also has additional probabilities known as emission probabilities. These describe the transition from the hidden states of your Hidden Markov model, which are parts of speech seen here as circles for noun, verb, and the other, to the observables or the words of your corpus shown here inside rectangles.
Here, for example, are the observables for the hidden states VB, which are the words; going, to, eat.
The emission probability from the hidden states, verb to the observable, eat, is 0.5.
This means when the model is currently at the hidden state for a verb, there is a 50 percent chance that the observable the model will emit is the word, eat.
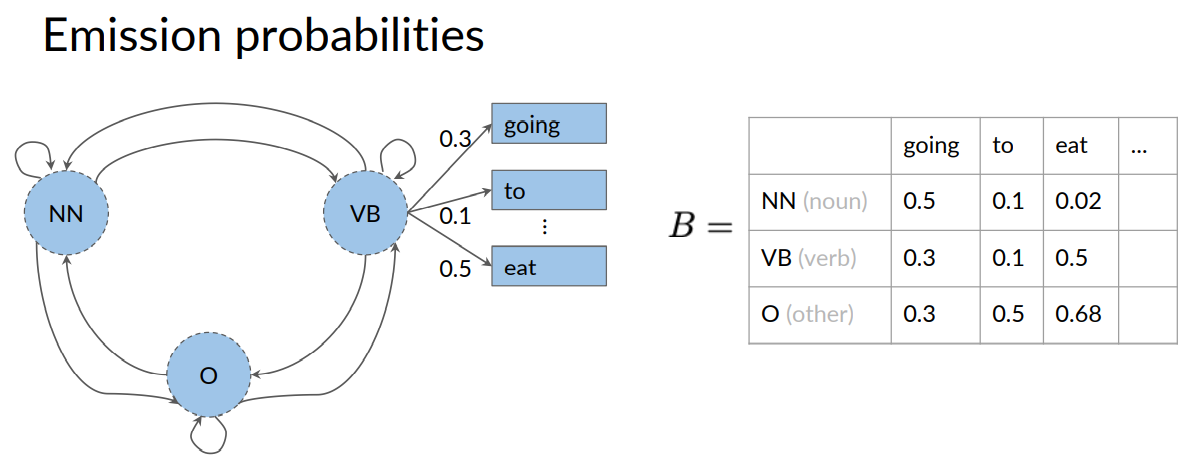
Here's an equivalent representation of the emission probabilities in the form of a table.
Each row is designated for one of the hidden states.
A column is designated for each of the observables. For example, the row for the hidden state, verb, intersects with the column for the observable, eat.
The value 0.5 is the emission probability of going from the states verb to emitting the observable, eat.
The emission matrix represents the probabilities for the transition of your end hidden states representing your parts of speech tags to the M words in your corpus.
Again, the row sum of probabilities is one.
What you might have realized in this example is that there are emission probabilities greater than zero for all three of our parts of speech tags. This is because words can have different parts of speech tag assigned depending on the context in which they appear.
For example, the word back should have different parts of speech tag in each of the sentences.
The noun tag for the sentence, he lay on his back, and the adverb tag for, I'll be back.
A quick recap of Hidden Markov models. They consist of a set of N states, Q.
The transition matrix A has dimension N by N, and the emission matrix B has dimension N by V.

Calculating Probabilities
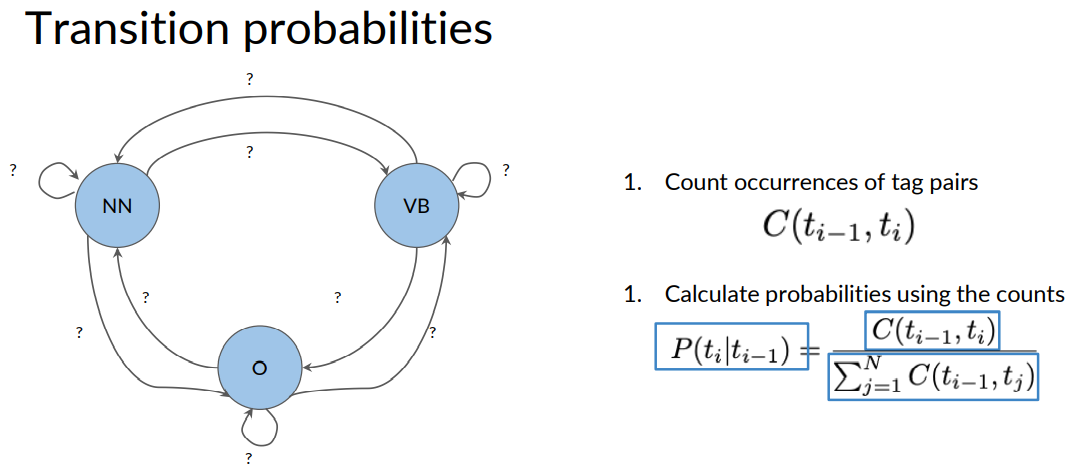
Let's start with how to populate the transition matrix, which holds all the transition probabilities between states of your Markov model.
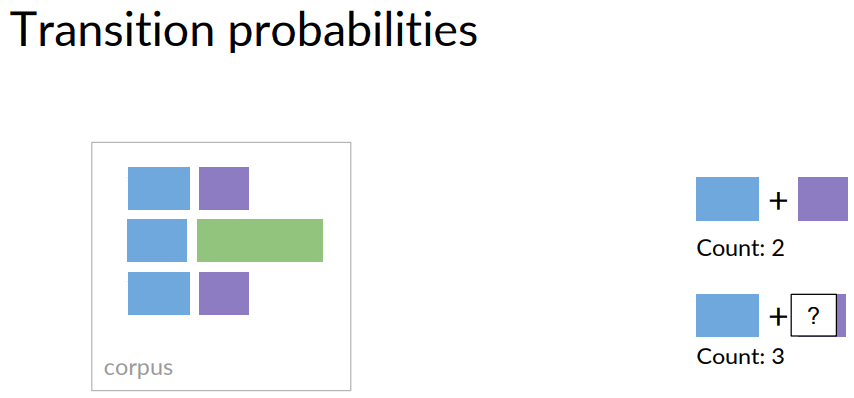
To calculate the transition probabilities, you actually only use the parts of speech tags from your training corpus, so to calculate the probability of the blue parts of speech tag, transitioning to the purple one, you first have to count the occurrences of that tag combination in your corpus, which is two.
The number of all tag pairs starting with a blue tag is three for this corpus at least.
Two out of three tag sequences in your training corpus starts with the blue parts of speech tag. In other words, the transition probability for a blue tag following a purple one is two out of three.
More formally, in order to calculate all the transition probabilities of your Markov model, you'd first have to count all occurrences of tag pairs in your training corpus.
Say you want to train a model for haiku, a type of shorts Japanese poetry. Your training corpus will be the following haiku from Ezra Pound written in 1913.
In the programming assignments, you'll be given a prepared corpus. Here, you'll make some changes to the corpus in order to calculate the correct probabilities.
Consider each line of the corpus as a separate sentence. First, at the start token to each line or sentence in order to be able to calculate the initial probabilities using the previous defined formula.
Then transform all words in the corpus to lowercase so the model becomes case insensitive.
The punctuation you should leave intact because it doesn't make a difference for a toy model, and there aren't tags for different kinds of punctuation included here. There you have it and nicely prepared corpus.


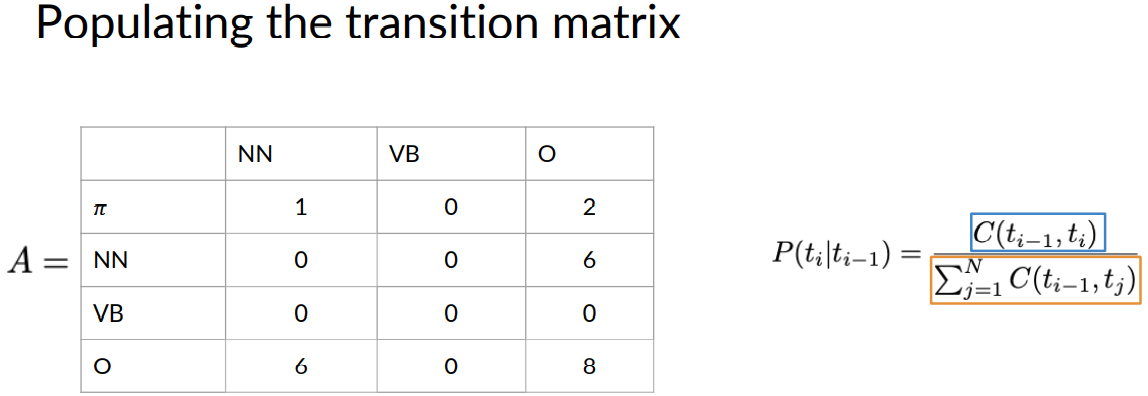
Populating the transition matrix
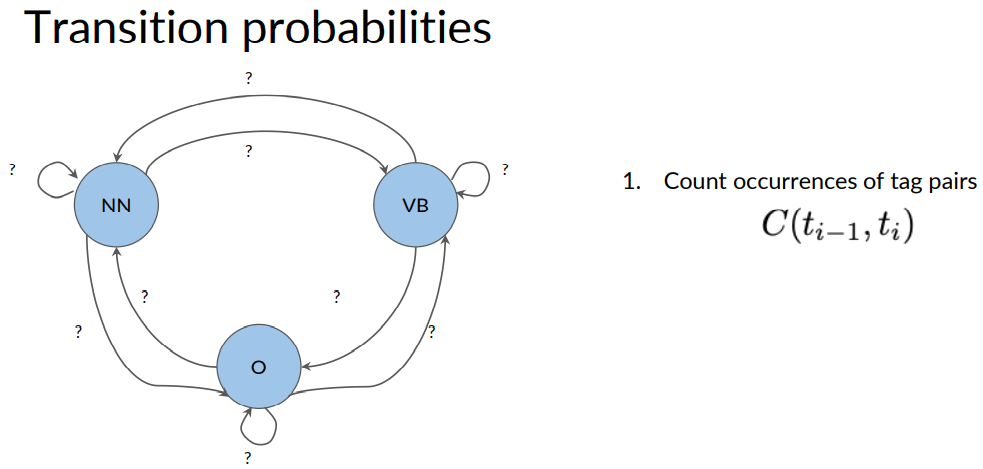
To populate the transition matrix, you need to calculate the probability of a tagging happening, given that's another tag already happened. You also need to calculate the probability that a tag happens at the beginning of the sentence.
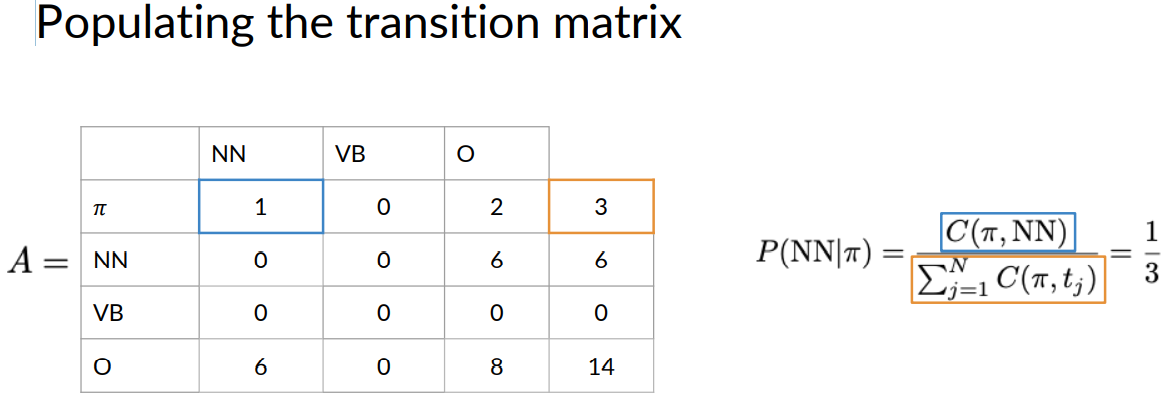
Begin by filling the first column of your matrix with the counts of the associated tags. Remember, the rows in the matrix represent the current states and the columns represent the next states.
The values represents the transition probabilities of going from the current state to the next state. The states for this use case is the parts of speech tag. As you can see, the defined tags and the elements in the corpus are marked with corresponding colors.
For the first column, you'll count the occurrences of the following tag combinations. As you see here, a noun following a start token occurs once in our corpus. A noun following a noun doesn't occur at all. A noun following a verb doesn't occur either.
A noun following another tag occurs six times. The rest of the matrix is populated accordingly.
You may have realized that the row sum of the VB tag is 0, which would lead to a division by 0 using this formula. The other is that in lots of entries in the transition matrix are 0, meaning that these transitions will have probability 0.
To handle this, change your formula slightly by adding a small value Epsilon to each of the counts in the numerator and add N times Epsilon to the divisor such that the row sums still adds up to one. This operation is also referred to as smoothing
If you substitute the Epsilon with a small value, say 0.001, then you'll get the following transition matrix.
The results of smoothing is, as you can see, that you no longer have any 0 value entries
Further, since the transition probabilities from the VB states are actually one-third for all outgoing transitions, they are equally likely. That's reasonable. Since you didn't have any data to estimate these transition probabilities.
One more thing before you go, and a real-world example, you might not want to apply smoothing to the initial probabilities in the first row of the transition matrix.
That's because if you apply smoothing to that row by adding a small value to possibly zeroed valued entries.
You'll effectively allow a sentence to start with any parts of speech tag, including punctuation.
Same is done in case of emission matrix as given below.