Word embeddings
-
Colab
Word embeddings are used in most NLP applications.
Whenever you are dealing with text, you first have to find a way to encode the words as numbers.
Word embedding are a very common technique that allows you to do so.
Here are a few applications of word embeddings that you should be able to implement by the time you complete the specialization.
Basic word representations could be classified into the following:
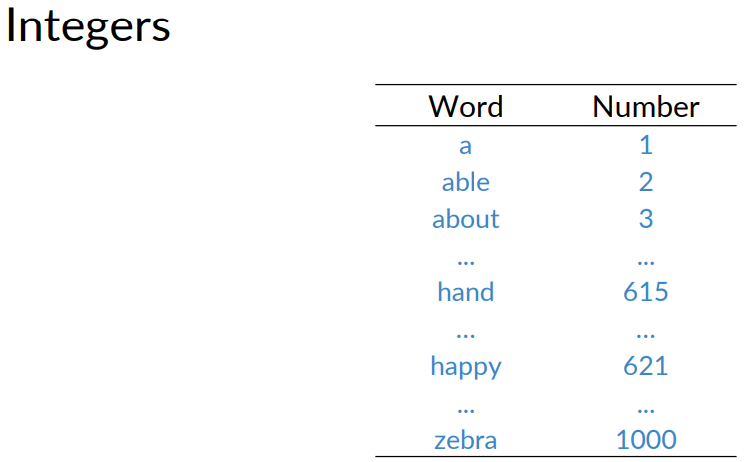
Integers: Below, you have an example where you use integers to represent a word. The issue there is that there is no reason why one word corresponds to a bigger number than another.
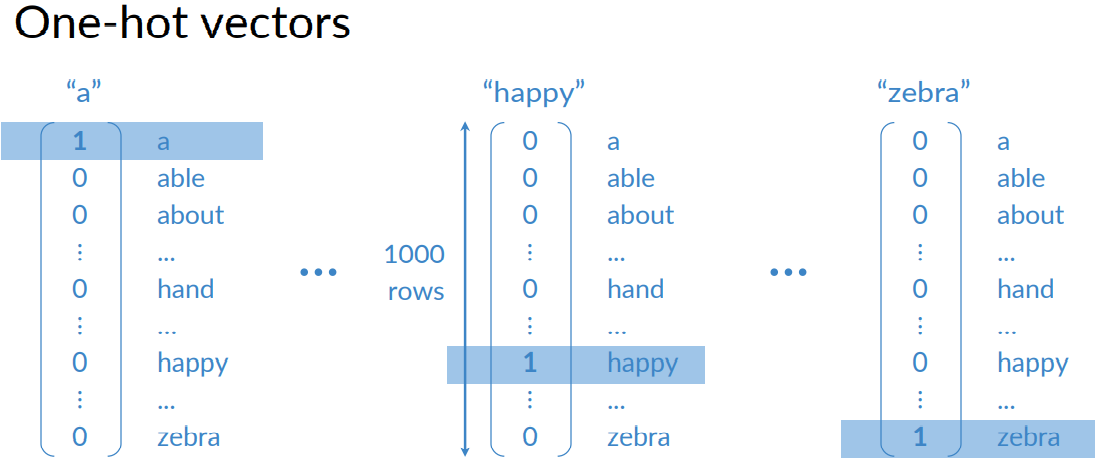
One-hot vectors: To fix this problem we introduce one hot vectors. To implement one hot vectors, you have to initialize a vector of zeros of dimension V and then put a 1 in the index corresponding to the word you are representing. The pros of one-hot vectors: simple and require no implied ordering. The cons of one-hot vectors: huge and encode no meaning.
Word embeddings: From the plot below, you can see that when encoding a word in 2D, similar words tend to be found next to each other. Perhaps the first coordinate represents whether a word is positive or negative. The second coordinate tell you whether the word is abstract or concrete. This is just an example, in the real world you will find embeddings with hundreds of dimensions. You can think of each coordinate as a number telling you something about the word. The pros: Low dimensions (less than V), Allow you to encode meaning


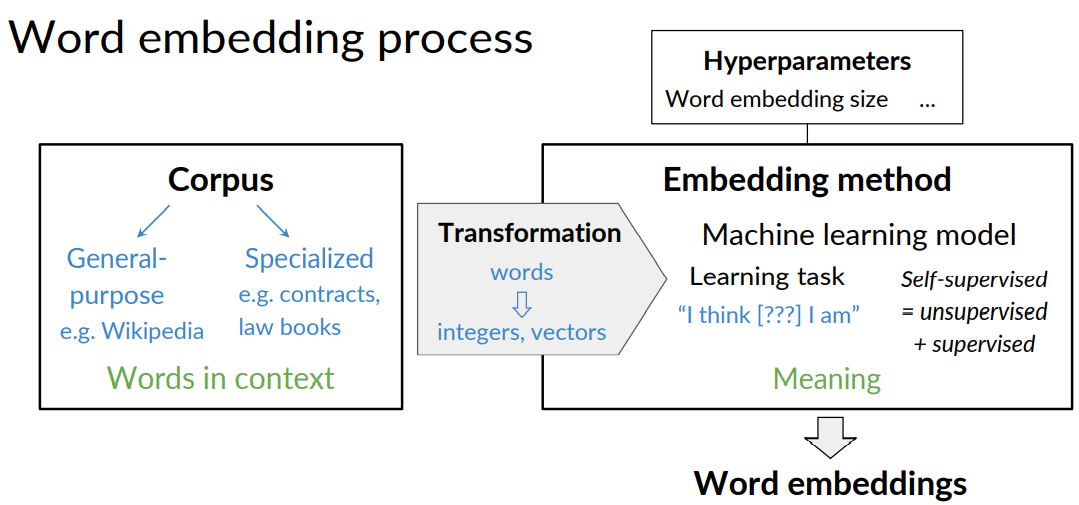
How to Create Word Embeddings?
To create word embeddings you always need a corpus of text, and an embedding method.
The context of a word tells you what type of words tend to occur near that specific word.
The context is important as this is what will give meaning to each word embedding.
Embeddings There are many types of possible methods that allow you to learn the word embeddings.
The machine learning model performs a learning task, and the main by-products of this task are the word embeddings.
The task could be to learn to predict a word based on the surrounding words in a sentence of the corpus, as in the case of the continuous bag-of-words.
The task is self-supervised: it is both unsupervised in the sense that the input data - the corpus - is unlabelled, and supervised in the sense that the data itself provides the necessary context which would ordinarily make up the labels.
When training word vectors, there are some parameters you need to tune. (i.e. the dimension of the word vector)
Classical Methods
Classical Methods
word2vec (Google, 2013)
Continuous bag-of-words (CBOW): the model learns to predict the center word given some context words.
Continuous skip-gram / Skip-gram with negative sampling (SGNS): the model learns to predict the words surrounding a given input word.
Global Vectors (GloVe) (Stanford, 2014): factorizes the logarithm of the corpus's word co-occurrence matrix, similar to the count matrix you��ve used before.
fastText (Facebook, 2016): based on the skip-gram model and takes into account the structure of words by representing words as an n-gram of characters. It supports out-of-vocabulary (OOV) words.
Deep learning, contextual embeddings
In these more advanced models, words have different embeddings depending on their context. You can download pre-trained embeddings for the following models.
BERT (Google, 2018):
ELMo (Allen Institute for AI, 2018)
GPT-2 (OpenAI, 2018)
Continuous Bag of Words Model
To create word embeddings, you need a corpus and a learning algorithm. The by-product of this task would be a set of word embeddings. In the case of the continuous bag-of-words model, the objective of the task is to predict a missing word based on the surrounding words.
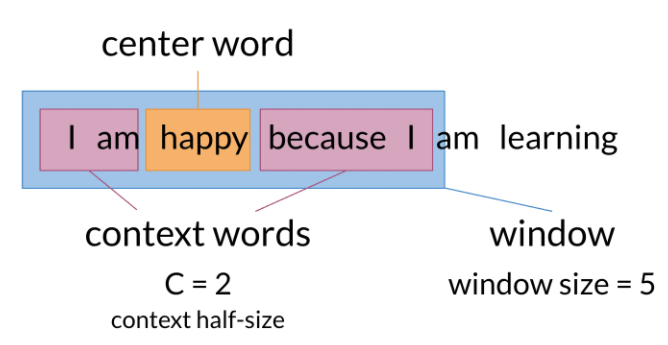
Here is a visualization that shows you how the models works.
As you can see, the window size in the image above is 5. The context size, C, is 2. C usually tells you how many words before or after the center word the model will use to make the prediction. Here is another visualization that shows an overview of the model.
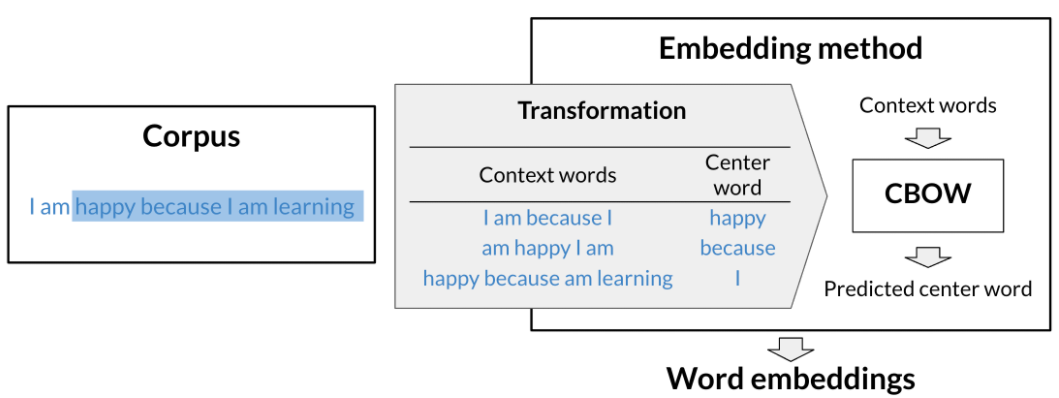
Transforming Words into Vectors
To transform the context vectors into one single vector, you can use the following.
As you can see, we started with one-hot vectors for the context words and and we transform them into a single vector by taking an average. As a result you end up having the following vectors that you can use for your training.
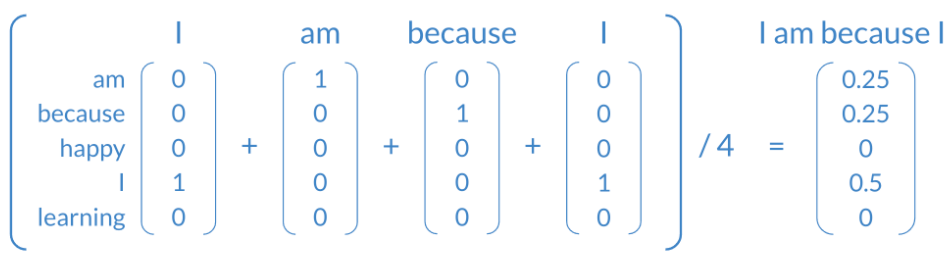

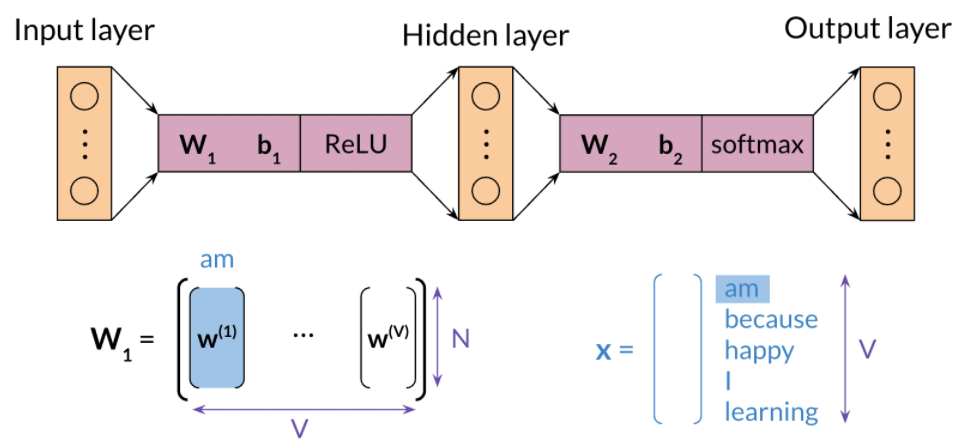
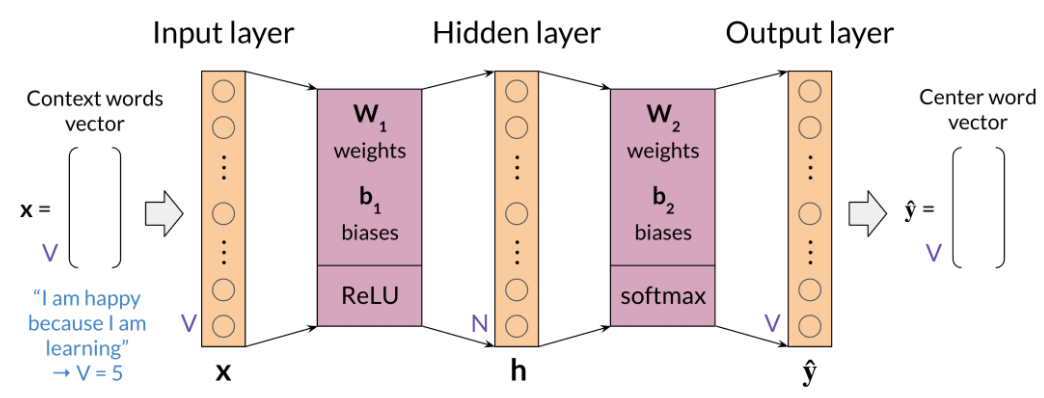
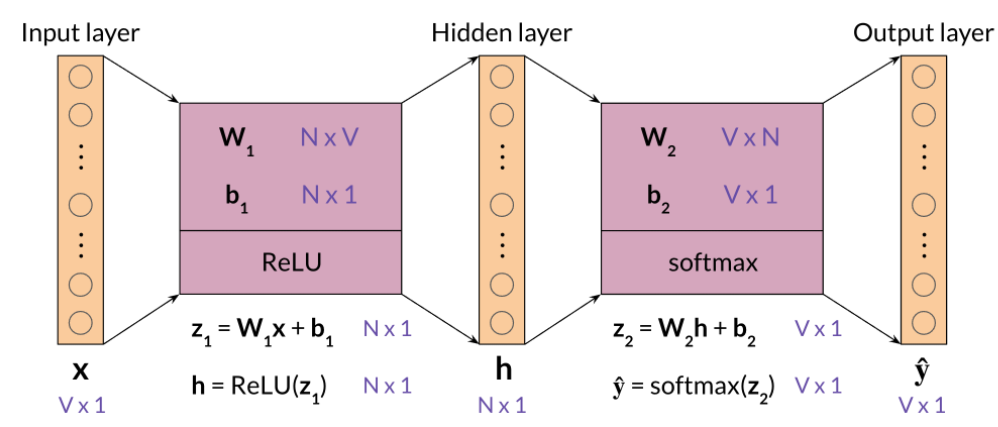
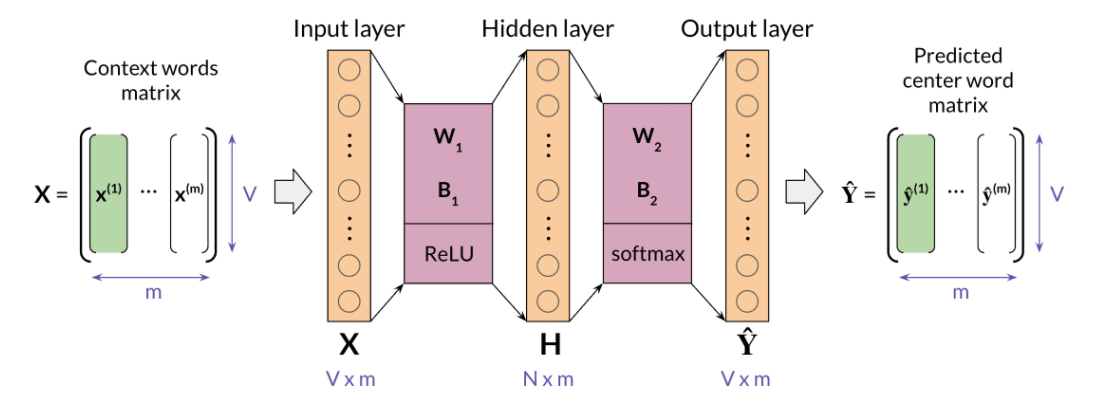
Architecture for the CBOW Model
The architecture for the CBOW model could be described as follows
You have an input, X, which is the average of all context vectors. You then multiply it by \(W_1\). and add \(b_1\).
The result goes through a ReLU function to give you your hidden layer. That layer is then multiplied by \(W_2\). and you add \(b_2\).
The result goes through a softmax which gives you a distribution over \(V\), vocabulary words.
You pick the vocabulary word that corresponds to the arg-max of the output.
When dealing with batch input, you can stack the examples as columns. You can then proceed to multiply the matrices as follows:
In the diagram above, you can see the dimensions of each matrix. Note that your \( \hat{Y}\) is of dimension V by m.
Each column is the prediction of the column corresponding to the context words.
So the first column in \( \hat{Y}\) is the prediction corresponding to the first column of X.
The cost function for the CBOW model is a cross-entropy loss defined as:
\(J=-\sum_{k=1}^{V} y_{k} \log \hat{y}_{k}\)
Gradient descent is used for finalizing the parameters and optimizing the model.
Extracting Word Embedding Vectors
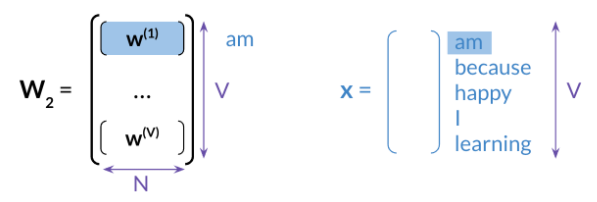
There are two options to extract word embeddings after training the continuous bag of words model. You can use \(w_1\) as follows:
If you were to use \(w_1\) , each column will correspond to the embeddings of a specific word. You can also use \(w_2\) as follows:
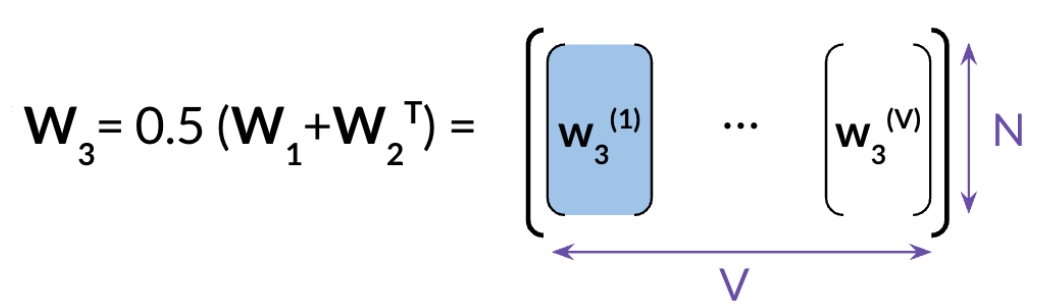
The final option is to take an average of both matrices as follows: