• Suppose the experiment about methods for quitting smoking were carried out with randomized assignments of subjects to the four treatments, and researchers determined that the percentage succeeding with the combination drug/therapy method was highest, and the percentage succeeding with no drugs or therapy was lowest.




• In other words, suppose there is clear evidence of an association between method used and success rate. Could it be concluded that the drug/therapy method causes success more than trying to quit without using drugs or therapy? Perhaps.




• Although randomized controlled experiments do give us a better chance of pinning down the effects of the explanatory variable of interest, they are not completely problem-free.




• For example, suppose that the manufacturers of the smoking cessation drug had just launched a very high-profile advertising campaign with the goal of convincing people that their drug is extremely effective as a method of quitting.




• Even with a randomized assignment to treatments, there would be an important difference among subjects in the four groups: those in the drug and combination drug/therapy groups would perceive their treatment as being a promising one, and may be more likely to succeed just because of added confidence in the success of their assigned method.




• Therefore, the ideal circumstance is for the subjects to be unaware of which treatment is being administered to them: in other words, subjects in an experiment should be (if possible) blind to which treatment they received.




• How could researchers arrange for subjects to be blind when the treatment involved is a drug? They could administer a placebo pill to the control group, so that there are no psychological differences between those who receive the drug and those who do not. The word "placebo" is derived from a Latin word that means "to please."




• It is so named because of the natural tendency of human subjects to improve just because of the "pleasing" idea of being treated, regardless of the benefits of the treatment itself. When patients improve because they are told they are receiving treatment, even though they are not actually receiving treatment, this is known as the placebo effect.




• Next, how could researchers arrange for subjects to be blind when the treatment involved is a type of therapy? This is more problematic. Clearly, subjects must be aware of whether they are undergoing some type of therapy or not. There is no practical way to administer a "placebo" therapy to some subjects. Thus, the relative success of the drug/therapy treatment may be due to subjects' enhanced confidence in the success of the method they happened to be assigned. We may feel fairly certain that the method itself causes success in quitting, but we cannot be absolutely sure.




• When the response of interest is fairly straightforward, such as giving up cigarettes or not, then recording its values is a simple process in which researchers need not use their own judgment in making an assessment.




• There are many experiments where the response of interest is less definite, such as whether or not a cancer patient has improved, or whether or not a psychiatric patient is less depressed. In such cases, it is important for researchers who evaluate the response to be blind to which treatment the subject received, in order to prevent the experimenter effect from influencing their assessments.




• If neither the subjects nor the researchers know who was assigned what treatment, then the experiment is called double-blind.




• The most reliable way to determine whether the explanatory variable is actually causing changes in the response variable is to carry out a randomized controlled double-blind experiment. Depending on the variables of interest, such a design may not be entirely feasible, but the closer researchers get to achieving this ideal design, the more convincing their claims of causation (or lack thereof) are.

View Answer



View Answer

• Some of the inherent difficulties that may be encountered in experimentation are the Hawthorne effect, lack of realism, noncompliance, and treatments that are unethical, impossible, or impractical to impose.




• We already introduced a hypothetical experiment to determine if people tend to snack more while they watch TV: Recruit participants for the study. While they are presumably waiting to be interviewed, half of the individuals sit in a waiting room with snacks available and a TV on. The other half sit in a waiting room with snacks available and no TV, just magazines. Researchers determine whether people consume more snacks in the TV setting.




• Suppose that, in fact, the subjects who sat in the waiting room with the TV consumed more snacks than those who sat in the room without the TV. Could we conclude that in their everyday lives, and in their own homes, people eat more snacks when the TV is on? Not necessarily, because people's behavior in this very controlled setting may be quite different from their ordinary behavior.




• If they suspect their snacking behavior is being observed, they may alter their behavior, either consciously or subconsciously. This phenomenon, whereby people in an experiment behave differently from how they would normally behave, is called the Hawthorne effect.




• Even if they don't suspect they are being observed in the waiting room, the relationship between TV and snacking there might not be representative of what it is in real life. One of the greatest advantages of an experiment—that researchers take control of the explanatory variable—can also be a disadvantage in that it may result in a rather unrealistic setting.




• Lack of realism (also called lack of ecological validity) is a possible drawback to the use of an experiment rather than an observational study to explore a relationship. Depending on the explanatory variable of interest, it may be quite easy or it may be virtually impossible to take control of the variable's values and still maintain a fairly natural setting.




• In our hypothetical smoking cessation example, both the observational study and the experiment were carried out on a random sample of 1,000 smokers with intentions to quit. In the case of the observational study, it would be reasonably feasible to locate 1,000 such people in the population at large, identify their intended method, and contact them again a year later to establish whether they succeeded or not.




• In the case of the experiment, it is not so easy to take control of the explanatory variable (cessation method) merely by telling all 1,000 subjects what method they must use. Noncompliance (failure to submit to the assigned treatment) could enter in on such a large scale as to render the results invalid. In order to ensure that the subjects in each treatment group actually undergo the assigned treatment, researchers would need to pay for the treatment and make it easily available.




• The cost of doing that for a group of 1,000 people would go beyond the budget of most researchers. Even if the drugs or therapy were paid for, it is very unlikely that most of the subjects contacted at random would be willing to use a method not of their own choosing, but dictated by the researchers. From a practical standpoint, such a study would most likely be carried out on a smaller group of volunteers, recruited via flyers or some other sort of advertisement.




• The fact that they are volunteers might make them somewhat different from the larger population of smokers with intentions to quit, but it would reduce the more worrisome problem of noncompliance. Volunteers may have a better overall chance of success, but if researchers are primarily concerned with which method is most successful, then the relative success of the various methods should be roughly the same for the volunteer sample as it would be for the general population, as long as the methods are randomly assigned. Thus, the most vital stage for randomization in an experiment is during the assignment of treatments, rather than the selection of subjects.




• There are other, more serious drawbacks to experimentation, as illustrated in the following hypothetical examples:




• Example : Suppose researchers want to determine if the drug Ecstasy causes memory loss. One possible design would be to take a group of volunteers and randomly assign some to take Ecstasy on a regular basis, while the others are given a placebo. Test them periodically to see if the Ecstasy group experiences more memory problems than the placebo group. The obvious flaw in this experiment is that it is unethical (and actually also illegal) to administer a dangerous drug like Ecstasy, even if the subjects are volunteers. The only feasible design to seek answers to this particular research question would be an observational study.




• Example : Suppose researchers want to determine whether females wash their hair more frequently than males. It is impossible to assign some subjects to be female and others male, and so an experiment is not an option here. Again, an observational study would be the only way to proceed.




• Example : Suppose researchers want to determine whether being in a lower income bracket may be responsible for obesity in women, at least to some extent, because they can't afford more nutritious meals and don't have the means to participate in fitness activities. The socioeconomic status of the study subject is a variable that cannot be controlled by the researchers, so an experiment is impossible. (Even if the researchers could somehow raise the money to provide a random sample of women with substantial salaries, the effects of their eating habits during their lives before the study began would still be present, and would affect the study's outcome.)




• These examples should convince you that, depending on the variables of interest, researching their relationship via an experiment may be too unrealistic, unethical, or impractical. Observational studies are subject to flaws, but often they are the only recourse.




1. Observational studies :




1. * The explanatory variable's values are allowed to occur naturally.




2. * Because of the possibility of lurking variables, it is difficult to establish causation.




3. * If possible, control for suspected lurking variables by studying groups of similar individuals separately.




4. * Some lurking variables are difficult to control for; others may not be identified.




2. Experiments :




1. * The explanatory variable's values are controlled by researchers (treatment is imposed).




2. * Randomized assignment to treatments automatically controls for all lurking variables.




3. * Making subjects blind avoids the placebo effect.




4. * Making researchers blind avoids conscious or subconscious influences on their subjective assessment of responses.




5. * A randomized controlled double-blind experiment is generally optimal for establishing causation.




6. * A lack of realism may prevent researchers from generalizing experimental results to real-life situations.




7. * Noncompliance may undermine an experiment. A volunteer sample might solve (at least partially) this problem.




8. * It is impossible, impractical or unethical to impose some treatments.

• Suppose researchers are not only interested in the effect of diet on blood pressure, but also the effect of two new drugs. Subjects are assigned to either Control Diet (no restrictions), Diet #1, or Diet #2, (the variable diet has, then, 3 possible values) and are also assigned to receive either Placebo, Drug #1, or Drug #2 (the variable Drug, then, also has three values).




• This is an example where the experiment has two explanatory variables and a response variable. In order to set up such an experiment, there has to be one treatment group for every combination of categories of the two explanatory variables. Thus, in this case there are 3 * 3 = 9 combinations of the two variables to which the subjects are assigned. The treatment groups are illustrated and labeled in the following table:




• 
  




• The column headings for the table are for the Diet variable: "No-diet", "Special diet 1" and "Special diet 2." The Rows are for the drug variable: "Placebo," "Drug 1," and "Drug 2."




• There are 9 cells in the table, one for every possible combination of row and column. These cells are labeled "tttX", where X is in the range of [1-9], representing each combination.




• Subjects would be randomly assigned to one of the nine treatment groups. If we find differences in the proportions of subjects who achieve the lower "moderate zone" blood pressure among the nine treatment groups, then we have evidence that the diets and/or drugs may be effective for reducing blood pressure.




• 
  




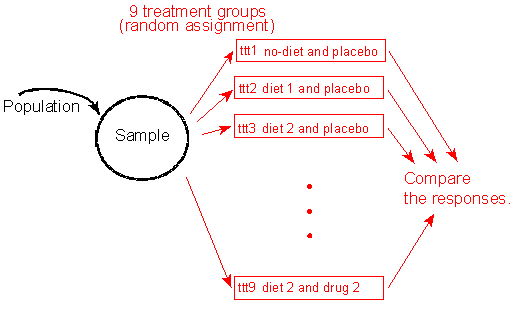
• From the population we generate a sample. The individuals of the sample are represented as a whole visually with a circle. These individuals are then divided by randomly assigning them to one of the 9 treatment groups. These treatment groups are "ttt1: no-diet and placebo,", "ttt2: diet 1 and placebo", "ttt3: diet 2 and placebo", and so on, up to "ttt9: diet 2 and drug 2." The responses from each of these treatment groups are compared.




• Comments 1. Recall that randomization may be employed at two stages of an experiment: in the selection of subjects, and in the assignment of treatments. The former may be helpful in allowing us to generalize what occurs among our subjects to what would occur in the general population, but the reality of most experimental settings is that a convenience or volunteer sample is used. Most likely the blood pressure study described above would use volunteer subjects. The important thing is to make sure these subjects are randomly assigned to one of the nine treatment combinations.




• In order to gain optimal information about individuals in all the various treatment groups, we would like to make assignments not just randomly, but also evenly. If there are 90 subjects in the blood pressure study described above, and 9 possible treatment groups, then each group should be filled randomly with 10 individuals. A simple random sample of 10 could be taken from the larger group of 90, and those individuals would be assigned to the first treatment group. Next, the second treatment group would be filled by a simple random sample of 10 taken from the remaining 80 subjects. This process would be repeated until all 9 groups are filled with 10 individuals each.

Solve the following

• Scenario: Online Statistics Course A university was interested in examining the overall effectiveness of its online statistics course, along with the effectiveness of particular aspects of the course. First, the university wanted to see whether the online course was better than a standard course. Second, the university wanted to know whether students learned best using Excel, using Minitab, or using no statistical package at all. The university randomly selected a group of 30 students and administered one of the different variants of the course (i.e., traditional or online, coupled with one of the software options) to each student. The success of each variant was measured by the students' average improvement between a pre-test and a post-test.

View Answer


View Answer


View Answer



View Answer



View Answer

• In some cases, an experiment's design may be enhanced by relaxing the requirement of total randomization and blocking the subjects first, dividing them into groups of individuals who are similar with respect to an outside variable that may be important in the relationship being studied. This can help ensure that the effect of treatments, as well as background variables, are most accurately measured.




• In blocking, we simply split the sampled subjects into blocks based upon the different values of the background variable, and then randomly allocate treatments within each block. Thus, blocking in the assignment of subjects is analogous to stratification in sampling.




• For example, consider again our experiment examining the differences between three versions of software from the last Learn By Doing activity. If we suspected that gender might affect individuals' software preferences, we might choose to allocate subjects to separate blocks, one for males and one for females. Within each block, subjects are randomly assigned to treatments and the treatment proceeds as usual. A diagram of blocking in this situation is below:




• 
  




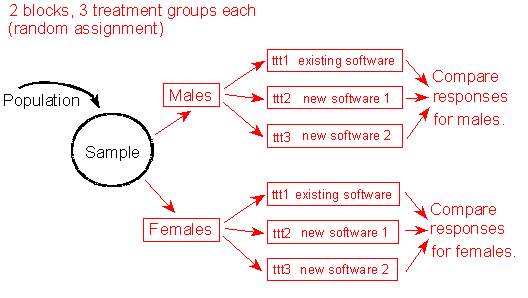
• We have 2 blocks, 3 treatment groups each (by random assignment). From the population we generate a sample. This sample of individuals is then split into two blocks, Males and Females. Each block is then randomly split further into the three treatment groups: "tt1: existing software," "ttt2 new software 1," and "ttt3 new software 2." So, we end up with 6 total groups. Within each group the responses from the treatment groups are compared to each other, generating results separately for each block.




• Example : Suppose producers of gasoline want to compare which of two types of gas results in better mileage for automobiles. In case the size of the vehicle plays a role in the effectiveness of different types of gasoline, they could first block by vehicle size, then randomly assign some cars within each block to Gasoline A and others to Gasoline B:




• 
  




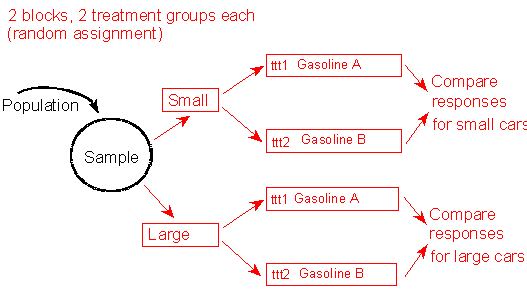
• This example consists of 2 blocks, 2 treatment groups each (by random assignment). From the population we generate a sample, then separate it into two blocks, "Small" and "Large," according to the vehicle size.; Within these blocks we randomly assign vehicles to use either Gasoline A or Gasoline B (So, each block is split into two treatment groups, "ttt1: Gasoline A", and "ttt2: Gasoline B"), resulting in 4 total groups. Then, within each block, we compare the responses, so we obtain results for each block individually.




• In the extreme, researchers may examine a relationship for a sample of blocks of just two individuals who are similar in many important respects, or even the same individual whose responses are compared for two explanatory values.




• Example : For example, researchers could compare the effects of Gasoline A and Gasoline B when both are used on the same car, for a sample of many cars of various sizes and models.




• 
  




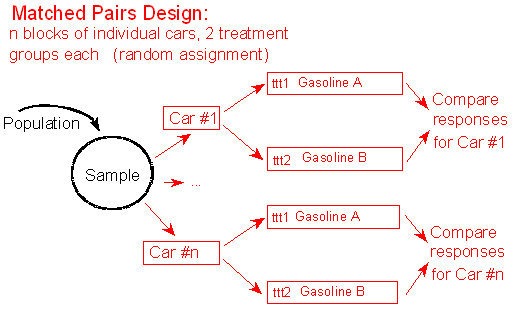
• In this Matched Pairs Design we have n blocks of individual cars, with 2 treatment groups each, done by random assignment. From the population we generate the sample group. The sample group is then placed into n blocks for each individual car. Each of these blocks is subjected to two treatments by random assignment. These treatments are "ttt1 Gasoline A" and "ttt2 Gasoline B." For each car, the responses to each treatment are compared, resulting in a treatment for each




• Such a study design, called matched pairs, may enable us to pinpoint the effects of the explanatory variable by comparing responses for the same individual under two explanatory values, or for two individuals who are as similar as possible except that the first gets one treatment, and the second gets another (or serves as the control). Treatments should usually be assigned at random within each pair, or the order of treatments should be randomized for each individual. In our gasoline example, for each car the order of testing (Gasoline A first, or Gasoline B first) should be randomized.




• Example : Suppose researchers want to compare the relative merits of toothpastes with and without tartar control ingredients. In order to make the comparison between individuals who are as similar as possible with respect to background and diet, they could obtain a sample of identical twins. One of each pair would randomly be assigned to brush with the tartar control toothpaste, while the other would brush with regular toothpaste of the same brand. These would be provided in unmarked tubes, so that the subjects would be blind. To make the experiment double-blind, dentists who evaluate the results would not know who used which toothpaste.




• 
  




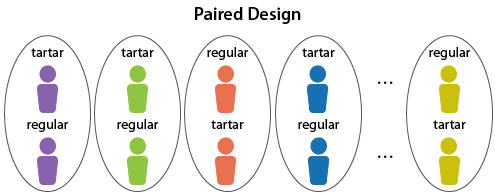
• Paired Design. There are n blocks, each represented by a circle with two identical twins in them. Randomly, the treatment of tartar or regular toothpaste is given to each twin. So, each circle has two twins, two types of toothpaste, and each twin randomly gets assigned one type of toothpaste.




• "Before-and-after" studies are another common type of matched pairs design. For each individual, the response variable of interest is measured twice: first before the treatment, then again after the treatment. The categorical explanatory variable is which treatment was applied, or whether a treatment was applied, to that participant.




• Comment : We have explained data production as a two-stage process: first obtain the sample, then evaluate the variables of interest via an appropriate study design. Even though the steps are carried out in this order chronologically, it is generally best for researchers to decide on a study design before they actually obtain the sample. For the toothpaste example above, researchers would first decide to use the matched pairs design, then obtain a sample of identical twins, then carry out the experiment and assess the results.

View Answer


View Answer

Previous

Next