Algorithms and Complexity
Algorithms
An algorithm is any well-defined computational procedure that takes some value, or set of values, as input and produces some value, or set of values, as output.
An algorithm is thus a sequence of computational steps that transform the input into the output.
Sorting Algorithms
Input: A sequence of n numbers {$a_1,a_2,...,a_n$}
Output: A permutation or reordering of {a'1,a'2, a'3...a'n} of the input sequence such that a'1 ≤ a'2 ≤ a'3 ≤ ... ≤ a'n
For example, given the input sequence h31; 41; 59; 26; 41; 58i, a sorting algorithm returns as output the sequence h26; 31; 41; 41; 58; 59i. Such an input sequence is called an instance of the sorting problem.
An algorithm is said to be correct if, for every input instance, it halts (finishes execution) with the correct output.
Data Structure
A data structure is a way to store and organize data in order to facilitate access and modifications. No single data structure works well for all purposes, and so it is important to know the strengths and limitations of several of them.
NP-Completeness A measure of efficiency of an algorithm is speed, i.e., how long an algorithm takes to produce its result. There are some problems, however, for which no efficient solution is known. An interesting subset of these problems are known as NP-complete.
No efficient algorithm for an NP-complete problem has ever been found
No one has proven that an efficient algorithm for one cannot exist. So no one knows whether or not efficient algorithms exist for NP-complete problems.
The set of NP-complete problems has the remarkable property that if an efficient algorithm exists for any one of them, then efficient algorithms exist for all of them.
If you can show that the problem is NP-complete, you can instead spend your time developing an efficient algorithm that gives a good, but not the best possible, solution.
Efficiency notes:
Insertion sort, takes time roughly equal to c1n2 to sort 'n' items, where c1 is a constant that does not depend on 'n'.
So it takes time roughly proportional to n2
Merge sort, takes time roughly equal to c2n log2 n where c2 is another constant that also does not depend on 'n'.
Insertion sort has a smaller constant factor than merge sort and so c1 < c2
Insertion sort usually runs faster than merge sort for small input sizes, once the input size 'n' becomes large enough, merge sort’s advantage of log2 n vs. n will compensate for the difference in constant factors. No matter how much smaller c2 is than c1 , there will always be a crossover point beyond which merge sort is faster. In general, as the problem size increases, so does the relative advantage of merge sort.
Q. Suppose we are comparing implementations of insertion sort and merge sort on the same machine. For inputs of size n, insertion sort runs in 8n2 steps, while merge sort runs in 64n lg n steps. For which values of n does insertion sort beat merge sort?
We wish to determine for which values of n the inequality 8n2 < 64 nlog2(n) holds. This happens when n < 8 log2 (n), or when n ≤ 43. In other words, insertion sort runs faster when we're sorting at most 43 items. Otherwise merge sort is faster.
Q. What is the smallest value of n such that an algorithm whose running time is 100n2 runs faster than an algorithm whose running time is 2n on the same machine?
We want that 100nn < 2n. note that if n = 14, this becomes 100(14)n = 19600 > 214 = 16384. For n = 15 it is 100(15)2 = 22500 < 215 = 32768. So, the answer is n = 15.
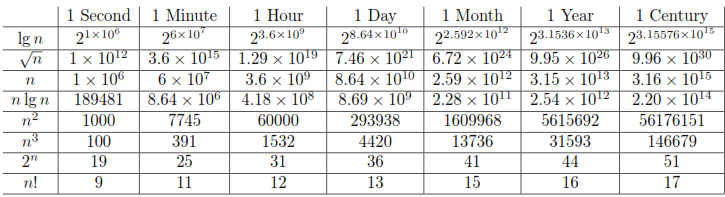
Q. For each function f (n) and time t in the following table, determine the largest size n of a problem that can be solved in time t , assuming that the algorithm to solve the problem takes f (n) microseconds.
Insertion Sort
Algorithm:
Input: A sequence of n numbers A = { $a_1,a_2,a_3, ... , a_n$ }
Output: A permutation or reordering of {a'1,a'2, a'3...a'n} of the input sequence such that a'1 ≤ a'2 ≤ a'3 ≤ ... ≤ a'n
INSERTION-SORT(A):
for j = 2 to A.length
key = A[j]
// Insert A[j] into the sorted sequence A[1 .. j-1]
i = j-1
while i > 0 and A[i] > key
A[i+1] = A[i]
i=i-1
A[i+1]=key
Cost of execution of Insertion Sort:

The running time of the algorithm is the sum of running times for each statement executed; a statement that takes ci steps to execute and executes n times will contribute cin to the total running time. i To compute T .n/, the running time of I NSERTION-SORT on an input of n values, we sum the products of the cost and times columns, obtaining
\( T(n) = c_1*n + c_2*(n-1) + c_4*(n-1) + c_5*\sum_{j=2}^{n} t_j + c_6 * \sum_{j=2}^{n} (t_j-1) + c_7 * \sum_{j=2}^{n} (t_j-1) + c_8*(n-1) \)
In INSERTION-SORT, the best case occurs if the array is already sorted as the T(n) function becomes a linear function in 'n'. If the array is in reverse sorted order the worst case results is seen as T(n) becomes a quadratic function in 'n'.
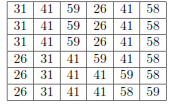
Q. illustrate the operation of INSERTION-SORT on the array A = { 31; 41; 59; 26; 41; 58 }
Q. Rewrite the INSERTION-SORT procedure to sort into non increasing instead of non decreasing order.
for j = 2 to A.length do
key = A[j]
// Insert A[j] into the sorted sequence A[1..j - 1].
i = j 1
while i > 0 and A[i] < key do
A[i + 1] = A[i]
i = i - 1
end while
end for
A[i + 1] = key
Q. Consider the searching problem:
Input: A sequence of n numbers A = { $a_1, a_2, ... , a_n$ } and a value 'v'.
Output: An index i such that v = A[i] or the special value NIL if 'v' does not appear in A.
Write pseudo-code for linear search, which scans through the sequence, looking for 'v'. Using a loop invariant, prove that your algorithm is correct. Make sure that your loop invariant fulfills the three necessary properties.
On each iteration of the loop body, the invariant upon entering is that there is no index k < j so that A[k] = v. In order to proceed to the next iteration of the loop, we need that for the current value of j, we do not have A[j] = v. If the loop is exited by line 5, then we have just placed an acceptable value in i on the previous line. If the loop is exited by exhausting all possible values of j, then we know that there is no index that has value j, and so leaving NIL in i is correct.
i = NIL
for j = 1 to A.length do
if A[j] = v then
i = j
return i
end if
return i
end for
Q. Consider the problem of adding two n-bit binary integers, stored in two n-element arrays A and B. The sum of the two integers should be stored in binary form in an .(n + 1) - element array C. State the problem formally and write pseudo-code for adding the two integers.
Input: two n-element arrays A and B containing the binary digits of two numbers a and b.
Output: an (n + 1)-element array C containing the binary digits of a + b.
carry = 0
for i=1 to n do
C[i] = (A[i] + B[i] + carry) (mod 2)
if A[i] + B[i] + carry ≥ 2 then
carry = 1
else
carry = 0
end if
end for
C[n+1] = carry
Worst-case analysis
The worst-case running time of an algorithm gives us an upper bound on the running time for any input. Knowing it provides a guarantee that the algorithm will never take any longer.
In analysis we consider only the leading term of a formula (e.g., an2), since the lower-order terms are relatively insignificant for large values of n.
We also ignore the leading term’s constant coefficient, since constant factors are less significant than the rate of growth in determining computational efficiency for large inputs.
We usually consider one algorithm to be more efficient than another if its worstcase running time has a lower order of growth. Due to constant factors and lowerorder terms, an algorithm whose running time has a higher order of growth might take less time for small inputs than an algorithm whose running time has a lower order of growth.
Q. Express the function n3 / 1000 - 100n2 - 100n + 3 in terms of Θ -notation.
n3 / 1000 - 100n2 - 100n + 3 is Θ(n3)
Q. Consider sorting n numbers stored in array A by first finding the smallest element of A and exchanging it with the element in A[1]. Then find the second smallest element of A, and exchange it with A[2]. Continue in this manner for the first n-1 elements of A. Write pseudocode for this algorithm, which is known as selection sort. What loop invariant does this algorithm maintain? Why does it need to run for only the first n - 1 elements, rather than for all n elements? Give the best-case and worst-case running times of selection sort in Θ-notation.
Input: An n-element array A.
Output: The array A with its elements rearranged into increasing order.
The loop invariant of selection sort is as follows: At each iteration of the for loop of lines 1 through 10, the subarray A[1..i - 1] contains the i - 1 smallest elements of A in increasing order. After n - 1 iterations of the loop, the n - 1 smallest elements of A are in the first n - 1 positions of A in increasing order, so the nth element is necessarily the largest element. Therefore we do not need to run the loop a final time. The best-case and worst-case running times of selection sort are Θ(n2). This is because regardless of how the elements are initially arranged, on the ith iteration of the main for loop the algorithm always inspects each of the remaining n - i elements to find the smallest one remaining.
for i = 1 to n - 1 do
min = i
for j = i + 1 to n do
// Find the index of the ith smallest element
if A[j] < A[min] then
min = j
end if
end for
Swap A[min] and A[i]
end for
This yields a running time of: $\sum_{i-1}^{n-1} n - i$ = Θ(n2)
Q. Consider linear search , How many elements of the input sequence need to be checked on the average, assuming that the element being searched for is equally likely to be any element in the array? How about in the worst case? What are the average-case and worst-case running times of linear search in ‚Θ -notation? Justify your answers.
Suppose that every entry has probability p of being the element looked for. Then, we will only check k elements if the previous k - 1 positiions were not the element being looked for, and the kth position is the desired value. Taking the expected value of this distribution we get it to be
$ (1-p)^{A.length} + \sum_{k = 1}^{A.length} k*(1-p)^{k-1} * p^k$
Q. How can we modify almost any algorithm to have a good best-case running time?
For a good best-case running time, modify an algorithm to first randomly produce output and then check whether or not it satisfies the goal of the algorithm.
If so, produce this output and halt. Otherwise, run the algorithm as usual. It is unlikley that this will be successful, but in the best-case the running time will only be as long as it takes to check a solution.
For example, we could modify selection sort to first randomly permut the elements of A, then check if they are in sorted order.
If they are, output A. Otherwise run selection sort as usual. In the best case, this modified algorithm will have running time Θ(n).
Divide and Conquer Approach
Approach involves break the problem into several subproblems that are similar to the original problem but smaller in size, solve the subproblems recursively, and then combine these solutions to create a solution to the original problem.
Divide the problem into a number of subproblems that are smaller instances of the same problem.
Conquer the subproblems by solving them recursively. If the subproblem sizes are small enough, however, just solve the subproblems in a straightforward manner.
Combine the solutions to the subproblems into the solution for the original problem.
MERGE SORT: MERGE and MERGE-SORT functions
MERGE(A,p,q,r)
n1 = q - p - 1
n2 = r - q
let L[1 ... n1 + 1] and R[1 ... n2 + 1] be new arrays
for i = 1 to n1
L[i] = A[p+i-1]
for j = 1 to n2
R[j] = A[q+j]
L[n1 + 1] = ∞
R[n2 + 1] = ∞
i = 1
j = 1
for k = p to r
if L[i] ≤ R[j]
A[k] = L[i]
i = i + 1
else A[k] = R[j]
j = j + 1
MERGE
MERGE-SORT(A,p,r)
if p < r
q = (p+r)/2
MERGE-SORT(A,p,q)
MERGE-SORT(A,q+1,r)
MERGE(A,p,q,r)
Analysis of Merge Sort
Divide: The divide step just computes the middle of the subarray, which takes constant time. Thus, D(n) = Θ(1)
Conquer: We recursively solve two subproblems, each of size \( \frac{n}{2} \) which contributes \( 2T(\frac{n}{2}) \) to the running time.
Combine: We have already noted that the MERGE procedure on an n-element subarray takes time Θ(n),and so C(n) = Θ(n)
When we add the functions D(n) and C(n) for the merge sort analysis, we are adding a function that is Θ(n) and a function that is Θ(1). This sum is a linear function of n, i.e. Θ(n). Adding it to the \( 2T (\frac{n}{2}) \) term from the “conquer” step gives the recurrence for the worst-case running time T(n) of merge sort:
\( T(n) = \left\{\begin{matrix} \Theta (1) & \text{; if n = 1}\\ 2T(\frac{n}{2}) + \Theta(n) & ; if n > 1 \end{matrix}\right. \)
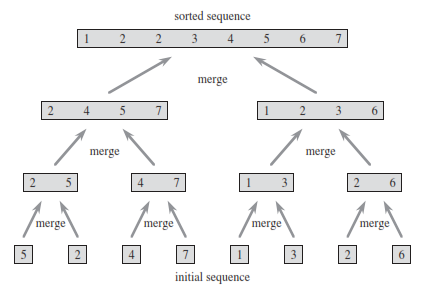
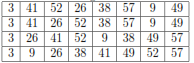
Q. illustrate the operation of merge sort on the array A = {3; 41; 52; 26; 38; 57; 9; 49}.
If we start with reading across the bottom of the tree and then go up level by level.
Q. Rewrite the MERGE procedure so that it does not use sentinels, instead stopping once either array L or R has had all its elements copied back to A and then copying the remainder of the other array back into A.
The following is a rewrite of MERGE which avoids the use of sentinels. Much like MERGE, it begins by copying the subarrays of A to be merged into arrays L and R. At each iteration of the while loop starting on line 13 it selects the next smallest element from either L or R to place into A. It stops if either L or R runs out of elements, at which point it copies the remainder of the other subarray into the remaining spots of A
MERGE(A,p,q,r)
n1 = q - p - 1
n2 = r - q
let L[1 ... n1 + 1] and R[1 ... n2 + 1] be new arrays
for i = 1 to n1
L[i] = A[p+i-1]
end for
for j = 1 to n2
R[j] = A[q+j]
end for
i = 1
j = 1
k = p
while i ≠ n1 and j ≠ n2
if L[i] ≤ R[j] then
A[k] = L[i]
i = i + 1
else A[k] = R[j]
j = j + 1
end if
k = k + 1
end while
if i = = n1 + 1 then
for m = j to n2 do
A[k] = R[m]
k = k + 1
end for
end if
if j = = n2 + 1 then
for m = i to n1 do
A[k] = L[m]
k = k + 1
end for
end if
Q. Use mathematical induction to show that when n is an exact power of 2,the solution of the recurrence T(n) = n lg n
\( T(n) = \left\{\begin{matrix} 2 & \text{; if n = 2}\\ 2T(\frac{n}{2}) + n & ; if n = 2^k, for k > 1 \end{matrix}\right. \)
Since n is a power of two, we may write n = 2k. If k = 1, then T(2) = 2 = 2 lg(2). Suppose it is true for k, we will show it is true for k + 1.
\( T(2^{k+1}) = 2T(\frac{2^{k+1}}{2}) + 2^{k+1} = 2T(2^{k}) + 2^{k+1} \)
\( 2(2^k lg (2^k)) + 2^{k+1} \)
\( k*2^{k+1} + 2^{k+1} \)
\( k*2^{k+1} + 2^{k+1} \)
\( (k+1)*2^{k+1} \)
\( 2^{k+1}lg(2^{k+1}) \)
n lg(n)
Q. We can express insertion sort as a recursive procedure as follows. In order to sort A[1...n], we recursively sort A[1...n-1] and then insert A[n] into the sorted array A[1...n-1]. Write a recurrence for the running time of this recursive version of insertion sort.
Let T(n) denote the running time for insertion sort called on an array of size n. We can express T(n) recursively as
\( \begin{cases}\Theta(1) & n \le c \\ T(n-1)I(n) & otherwise\end{cases} \)
where I(n) denotes the amount of time it takes to insert A[n] into the sorted array A[1...n 1]. As seen before, I(n) is Θ(log n).
Q. The binary search algorithm repeats this procedure, halving the size of the remaining portion of the sequence each time. Write pseudocode, either iterative or recursive, for binary search. Argue that the worst-case running time of binary search is Θ (lg n).
The following recursive algorithm gives the desired result when called with a = 1 and b = n.
BinSearch(a,b,v)
if then a > b
return NIL
end if
m = (a+b)/2
if then m = v
return m
end if
if then m < v
return BinSearch(a,m,v)
end if
return BinSearch(m+1,b,v)
Note that the initial call should be BinSearch(1, n, v). Each call results in a constant number of operations plus a call to a problem instance where the quantity b - a falls by at least a factor of two. So, the runtime satis es the recurrence T(n) = T(n/2) + c. So, T(n) ∈ Θ(lg(n))
Q. Observe that the while loop of lines 5–7 of the INSERTION-SORT procedure uses a linear search to scan (backward) through the sorted subarray A[1...j-1]. Can we use a binary search instead to improve the overall worst-case running time of insertion sort to Θ (n lg n)?
A binary search wouldn't improve the worst-case running time.
Insertion sort has to copy each element greater than key into its neighboring spot in the array.
Doing a binary search would tell us how many how many elements need to be copied over, but wouldn't rid us of the copying needed to be done.
Q. Describe a Θ(n lg n) time algorithm that, given a set S of n integers and another integer x, determines whether or not there exist two elements in S whose sum is exactly x
Use Merge Sort to sort the array A in time Θ(n lg(n))
i = 1
j = n
while i < j do
if A[j] + A[j] = S then
return true
end if
if A[i] + A[j] < S then
i = i + 1
end if
if A[i] + A[j] > S then
j = j - 1
end if
end while
return false
Bubble Sort
BUBBLESORT(A)
for i = 1 to A.length - 1
for j = A.length downto i + 1
if A[j] < A[j-1]
exchange A[j] with A[j-1]
The best case and worst case running time of bubble sort is Θ(n2)
Solved Question Papers
Q. 2 Assume that the algorithms considered here sort the input sequences
in ascending order. If the input is already in ascending order, which of the
following are TRUE?
I. Quick sort runs in θ(n2) time
II. Bubble sort runs in θ(n2)time
III. Merge sort runs in θ(n) time
IV. Insertion sort runs in θ(n) time. (GATE 2016 SET B)
I and II only
I and II only
II and IV only
I and IV only
Ans . D
Solution steps: As input is already sorted quick sort runs in θ(n2) and insertion sort runs in θ(n).
Q.3 The worst case running times of Insertion sort, Merge sort and Quick sort, respectively, are: (GATE 2016 SET A)
θ(nlogn), θ(nlogn), and θ(n2)
θ(n2),θ(n2), and θ(nlogn)
θ(n2), θ(nlogn), and θ(nlogn)
θ(n2), θ(nlogn), and θ(n2)
Ans : (D)
Solution steps:
Merge sort θ(nlogn) in all the cases.We always divide array in two halves, sort the two halves and merge them. The recursive formula is T(n) = 2T(n/2) + θ(n)
Quick sort takes θ(n2) in worst case. In QuickSort, we take an element as pivot and partition the array around it. In worst case, the picked element is always a corner element and recursive formula becomes T(n) = T(n-1) + θ(n). An example scenario when worst case happens is, arrays is sorted and our code always picks a corner element as pivot.
Insertion sort takes θ(n2) in worst case as we need to run two loops. The outer loop is needed to one by one pick an element to be inserted at right position. Inner loop is used for two things, to find position of the element to be inserted and moving all sorted greater elements one position ahead. Therefore the worst case recursive formula is T(n) = T(n-1) + θ(n).
Q. What is the number of swaps required to sort n elements using selection sort, in the worst case? (GATE 2009)
(A) θ(n)
(B) θ(n log n)
(C) θ(n)
(D) θ(nlog n)
Ans . A
If there are n elements then in worst case , total no of swaps will be (n-1) in slection sort. so the no of swaps is (n).
Q.3 Consider the C function given below. Assume that the array listA contains n (> 0) elements, sorted in ascending order.
Which one of the following statements about the function ProcessArray is CORRECT? (GATE 2014 SET 3)
It will run into an infinite loop when x is not in listA.
It is an implementation of binary search.
It will always find the maximum element in listA.
It will return −1 even when x is present in listA.
Ans . 2.It is an implementation of binary search.
The function is iterative implementation of Binary Search.
k keeps track of current middle element.
i and j keep track of left and right corners
of current subarray
Q. Output of following program?
#include <stdio.h>
int fun(int n, int *f_p)
{
int t, f;
if (n <= 1)
{
*f_p = 1;
return 1;
}
t = fun(n- 1,f_p);
f = t+ * f_p;
*f_p = t;
return f;
}
int main()
{
int x = 15;
printf (" %d \n", fun(5, &x));
return 0;
}
(GATE 2009)
6
8
14
15
Ans: B
Q.2 Which one of the following is the tightest upper bound that represents the number of swaps required to sort n numbers using selection sort? (GATE 2013)
O(log n)
- O(n)
- O(nLogn)
- O(n^2)
Ans . 2
-
Merge sort
-
Bubble sort
-
Quick sort
-
Selection sort
-
O(n)
-
O(n Log n)
-
O()
-
O(n!)
-
O(log n)
-
O(n)
-
O(nLogn)
-
\(O\left(n^{2}\right)\)
A
- B
- C
- D
- Time complexity of Heap Sort is \(\ominus\left(m\log{m}\right)\) for m input elements.
- For m = \(\ominus\left(logn / (log log n)\right)\), the value of \(\ominus\left(m*log{m}\right)\) will be \(\ominus\left(( [Log n/(Log Log n)] * [Log (Log n/(Log Log n))] )\right)\) which will be \(\ominus\left(( [Log n/(Log Log n)] * [ Log Log n - Log Log Log n] )\right)\) which is \(\ominus\left(\log{n}\right)\)
- Here we have to tell the value of k returned not the time complexity.
>for (i = n/2; i <= n; i++)
for (j = 2; j <= n; j = j * 2)
k = k + n/2;
return k;
The outer loop runs (n/2) times The inner loop runs logn times.(\((2^{k})\) = n => k = logn). Now looking at the value of k in inner loop, n is added to k, logn times as the inner loop is running logn times. Therefore the value of k after running the inner loop one time is (n*logn). - Therefore total time complexity is inner multiplied with outer loop complexity which (n for outer and nlogn for inner) \((n^{2logn})\).
Quick sort
Insertion sort
Selection sort
Heap sort
For selection sort, number of swaps required is minimum ( T(n) ).
$$\theta (n\log n) $$
$$\theta ({n^2})$$
$$\theta (n)$$
$$\theta (\log n)$$
-
O(1)
-
O(Logn)
-
O(n)
-
O(nLogn)
logn
n
2n + 1
\((2^n - 1)\)
For a right skewed binary tree, number of nodes will be 2^n – 1. For example, in below binary tree, node ‘A’ will be stored at index 1, ‘B’ at index 3, ‘C’ at index 7 and ‘D’ index15.
A
\
\
B
\
\
C
\
\
D
10, 20, 15, 23, 25, 35, 42, 39, 30
- 15, 10, 25, 23, 20, 42, 35, 39, 30
- 15, 20, 10, 23, 25, 42, 35, 39, 30
- 15, 10, 23, 25, 20, 35, 42, 39, 30
Solution:
To sort elements in increasing order, selection sort always picks the maximum element from remaining unsorted array and swaps it with the last element in the remaining array.
So the number of swaps, it makes in n-1 which is O(n).
Q. Which of the following sorting algorithms has the lowest worst-case complexity? (GATE 2007)
Ans. 1
| ALGORITHM | WORST CASE TIME COMPLEXITY |
|---|---|
| MERGE SORT | \[o\left(N \log N\right)\] |
| BUBBLE SORT | \[o\left(N*N\right)\] |
| QUICKSORT | \[o\left(N*N\right)\] |
| SELECTION SORT | \[o\left(N*N\right)\] |
Q. Randomized quicksort is an extension of quicksort where the pivot is chosen randomly. What is the worst case complexity of sorting n numbers using randomized quicksort? (GATE 2001)
Ans. 3
Explanation:
Randomized quicksort has expected time complexity as O(nLogn), but worst case time complexity remains same. In worst case the randomized function can pick the index of corner element every timeQ. Which one of the following is the tightest upper bound that represents the number of swaps required to sort n numbers using selection sort? (GATE 2013)
Ans. 2
Solution:
To sort elements in increasing order, selection sort always picks the maximum element from remaining unsorted array and swaps it with the last element in the remaining array.
So the number of swaps, it makes in n-1 which is O(n).
Q. The number of elements that can be sorted in \(\ominus\left(\log{n}\right)\) time using heap sort is (GATE 2013)

Ans. 4
Solution:
Ans. 2
Solution:
Q. Which one of the following in place sorting algorithms needs the minimum number of swaps? (GATE 2006)
Ans . (C) Selection sort
Q. The worst case running time to search for an element in a balanced in a binary search tree with n2^n elements is (GATE 2012)
Ans . 3
The search time in a binary search tree depends on the form of the tree, that is on the order in which its nodes were inserted. A pathological case: The n nodes were inserted by increasing order of the keys, yielding something like a linear list (but with a worse space consumption), with O(n) search time(in the case of skew tree). -> A balanced tree is a tree where every leaf is “not more than a certain distance” away from the root than any other leaf.So in balanced tree, the height of the tree is balanced to make distance between root and leafs nodes a low as possible. In a balanced tree, the height of tree is log2(n). -> So , if a Balanced Binary Search Tree contains n2n elements then Time complexity to search an item: Time Complexity = log(n2n) = log (n) + log(2n) = log (n) +n = O(n) So Answer is 3
Q. Which one of the following is the tightest upper bound that represents the time complexity of inserting an object into a binary search tree of n nodes? (GATE 2013)
Ans. 3
Solution:
To insert an element, we need to search for its place first. The search operation may take O(n) for a skewed tree like following.
To insert 50, we will have to traverse all nodes. 10 - 20 - 30 - 40
Q. A scheme for storing binary trees in an array X is as follows. Indexing of X starts at 1 instead of 0. the root is stored at X[1]. For a node stored at X[i], the left child, if any, is stored in X[2i] and the right child, if any, in X[2i+1]. To be able to store any binary tree on n vertices the minimum size of X should be. (GATE 2006)
Ans . (D) \((2^n-1)\)
Q. The preorder traversal sequence of a binary search tree is 30, 20, 10, 15, 25, 23, 39, 35, 42. Which one of the following is the postorder traversal sequence of the same tree? (GATE 2013)
Ans. 4
Solution:
In order to construct a binary tree from given traversal sequences, one of the traversal sequence must be Inorder. The other traversal sequence can be either Preorder or Postorder.
We know that the Inorder traversal of Binary Search Tree is always in ascending order so the Inorder Traversal would be the ascending order of given Preorder traversal i.e 10, 15, 20, 23, 25, 30, 35, 39, 42.
Now we have to construct a tree from given Inorder and Preorder traversals.
