FINITE AUTOMATA - Background
Several games that children play fit the following description. Pieces are set up on a playing board.
Dice are thrown (or a wheel is spun), and a number is generated at random. Depending on the number, the pieces on the board must be rearranged in a fashion completely specified by the rules.
The child has no options about changing the board. Everything is determined by the dice. Usually it is then some other child's turn to throw the dice and make his or her move, but this hardly matters, since no skill or choice is involved.
We could eliminate the opponent and have the one child move first the white pieces and then the black.
Whether or not the white pieces win the game is dependent entirely on what sequence of numbers is generated by the dice, not on who moves them.
Let us look at all possible positions of the pieces on the board and call them states. The game changes from one state to another in a fashion determined by the input of a certain number.
For each possible number there is one and only one resulting state. We should allow for the possibility that after a number is entered the game is still in the same state as it was before.
(For example, if a player who is in "jail" needs to roll doubles in order to get out, any other roll leaves the board in the same state.)
After a certain number of rolls, the board arrives at a state that means a victory for one of the players and the game is over. We call this a final state.
There might be many possible final states. In Computer Theory these are also called halting states or terminal states or accepting states.
Finite automata - Computer theory
A child has a simple computer (input device, processing unit, memory, output device) and wishes to calculate the sum of 3 plus 4.
The child writes a program, which is a sequence of instructions that are fed into the machine one at a time.
Each instruction is executed as soon as it is read, and then the next instruction is read.
If all goes well, the machine outputs the number 7 and terminates execution.
We can consider this process to be similar to the boardgame. Here the board is the computer and the different arrangements of pieces on the board correspond to the different arrangements of 0's and 1's in the cells of memory.
Two machines are in the same state if their output pages look the same and their memories look the same cell by cell.
The computer is also deterministic, by which we mean that, on reading one particular input instruction, the machine converts itself from one given state to some particular other state (or remains in the same state if given a NO-OP) where the resultant state is completely determined by the prior state and the input instruction.
We can consider the set of all computer instructions as the letters of an alphabet. We can then define a language to be the set of all words over this alphabet that lead to success. This is the language with words that are all programs that print a 7
The most general model, of which both of these examples are instances, is called a finite automaton-"finite" because the number of possible states and number of letters in the alphabet are both finite, and "automaton" because the change of states is totally governed by the input.
It is automatic (involuntary and mechanical) not willful, just as the motion of the hands of a clock is automatic while the motion of the hands of a human is presumably the result of desire and thought.
A finite automaton is a collection of three things
A finite set of states, one of which is designated as the initial state, called the start state, and some (maybe none) of which are designated as final states.
An alphabet Σ of possible input letters, from which are formed strings, that are to be read one letter at a time
A finite set of transitions that tell for each state and for each letter of the input alphabet which state to go to next.
Finite Automata
The definition above is incomplete in the sense that it describes what a finite automation is but not how it works.
It works by being presented with an input string of letters that it reads letter by letter starting at the leftmost letter. Beginning at the start state the letters determine a sequence of states. The sequence ends when the last input letter has been read.
Instead of writing out the whole phrase "finite automaton" it is customary to refer to one by its initials, FA. The term FA is read by naming its letters, so we say "an FA" even though it stands for "a finite automaton" and we say "two FA's" even though it stands for "two finite automata".
Some people prefer to call the object we have just defined a finite acceptor because its sole job is to accept certain input strings and run on them. It does not do anything like print output or play music. Even so, we shall stick to the terminology "finite automaton."
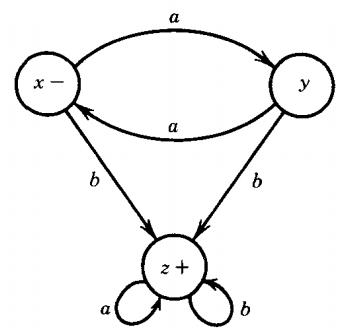
Suppose that the input alphabet has only the two letters a and b. Let us also assume that there are only three states, x, y, and z. Let the following be the rules of transition:
1. From state x and input a go to state y.
2. From state x and input b go to state z.
3. From state y and input a go to state x.
4. From state y and input b go to state z.
5. From state z and any input stay at state z.
Let us also designate state x as the starting state and state z as the only final state.
We now have a perfectly defined finite automaton, since it fulfills all three requirements demanded above: states, alphabet, transitions.
Let us examine what happens to various input strings when presented to this FA. Let us start with the string aaa. We begin, as always, in state x. The first letter of the string is an a, and it tells us to go to state y (by Rule 1).
The next input (instruction) is also an a, and this tells us by Rule 3 to go back to state x. The third input is another a, and by Rule 1 again we go to state y. There are no more input letters in the input string, so our trip has ended. We did not finish up in the final state (state z), so we have an unsuccessful termination of our run.
The string aaa is not in the language of all strings that leave this FA in state z. The set of all strings that do leave us in a final state is called the language defined by the finite automaton.
The input string aaa is not in the language defined by this FA. Using other terminology, we may say that the string aaa is not accepted by this finite automaton because it does not lead to a final state.
We use this expression often. We may also say "aaa is rejected by this FA." The set of all strings accepted is the language associated with the FA.
We say, this FA accepts the language L, or L is the language accepted by this FA. When we wish to be anthropomorphic, we say that L is the language of the FA.
If language L1 is contained in language L2 and a certain FA accepts L2 (all the words in L2 are accepted and all the inputs accepted are words in L2), then this FA also must accept all the words in language L, (since they are also words in L2).
However, we do not say "L1 is accepted by this FA" since that would mean that all the words the FA accepts are in L1.
This is solely a matter of standard usage. At the moment, the only job an FA does is define the language it accepts which is a fine reason for calling it an acceptor, or better still a language recognizer.
Let us examine a different input string for this same FA. Let the input be abba. As always, we start in state x. Rule 1 tells us that the first input letter, a, takes us to state y.
Once we are in state y we read the second input letter, which is a b. Rule 4 now tells us to move to state z.
The third input letter is a b, and since we are in state z, Rule 5 tells us to stay there. The fourth input letter is an a, and again Rule 5 says stay put. Therefore, after we have followed the instruction of each input letter we end up in state z.
State z is designated a final state, so we have won this game. The input string abba has taken us successfully to the final state. The string abba is therefore a word in the language associated with this FA. The word abba is accepted by this FA.
It is not hard for us to predict which strings will be accepted by this FA. If an input string is made up of only the letter a repeated some number of times, then the action of the FA will be to jump back and forth between state x and state y.
No such word can ever be accepted. To get into state z, it is necessary for the string to have the letter 'b' in it.
As soon as a 'b' is encountered in the input string, the FA jumps immediately to state z no matter what state it was in before.
Once in state z, it is impossible to leave. When the input string runs out, the FA will still be in state z, leading to acceptance of the string.
The FA above will accept all strings that have the letter b in them and no other strings.
Therefore, the language associated with (or accepted by) this FA is the one defined by the regular expression (a + b)*b(a + b)*
The list of transition rules can grow very long. It is much simpler to summarize them in a table format. Each row of the table is the name of one of the states in the FA, and each column of the table is a letter of the input alphabet.
The entries inside the table are the new states that the FA moves into-the transition states. The transition table for the FA we have described is:
We have also indicated along the left side which states are start and final states. This table has all the information necessary to define an FA.
Even though it is no more than a table of symbols, we consider an FA to be a machine, that is, we understand that this FA has dynamic capabilities. It moves. It processes input.
Something goes from state to state as the input is read in and executed. We may imagine that the state we are in at any given time is lit up and the others are dark. An FA running on an input string then looks like a pinball machine.
From the table format it is hard to see the moving parts. There is a pictorial representation of an FA that gives us more of a feel for the motion.
We begin by representing each state by a small circle drawn on a sheet of paper. From each state we draw arrows showing to which other states the different letters of the input alphabet will lead us.
We label these arrows with the corresponding alphabet letters. If a certain letter makes a state go back to itself, we indicate this by an arrow that returns to the same circle-this arrow is called a loop.
We can indicate the start state by labeling it with the word "start" or by a minus sign, and the final states by labeling them with the word "final" or plus signs.
The machine we have already defined by the transition list and the transition table can be depicted by the transition diagram:
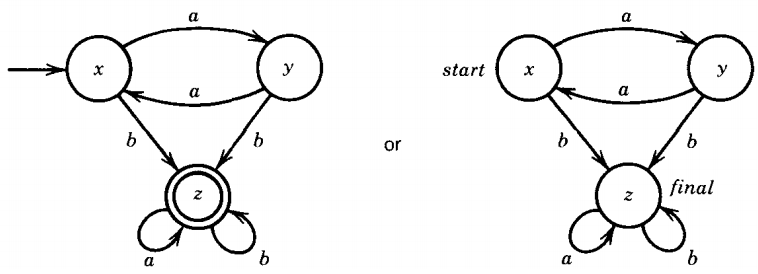
Sometimes a start state is indicated by an arrow and a final state by drawing a box or another circle around its circle. The minus and plus signs, when employed, are drawn inside or outside the state circles. This machine can also be depicted as:
Every input string can be interpreted as traversing a path beginning at the start state and moving among the states (perhaps visiting the same state many times) and finally settling in some particular rest state.
If it is a final state, then the path has ended in success. The letters of the input string dictate the directions of travel. They are the map and the fuel needed for motion. When we are out of letters we must stop.
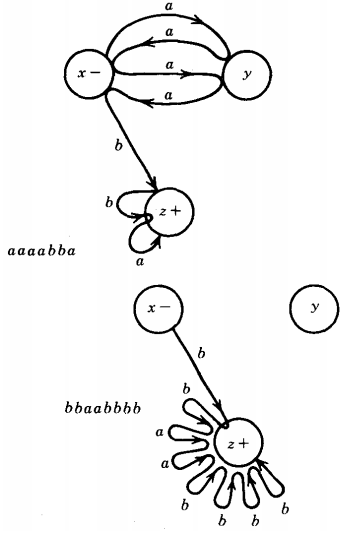
Let us look at this machine again and at the paths generated by the input strings aaaabba and bbaabbbb.
When we depict an FA as circles and arrows, we say that we have drawn a directed graph. Graph Theory is an exciting subject in its own right, but for our purposes there is no real need to understand directed graphs in any deeper sense than as a collection of circles and arrows.
We borrow from Graph Theory the name directed edge or simply edge for the arrow between states. An edge comes from one state and leads to another (or the same, if it is a loop).
Every state has as many outgoing edges as there are letters in the alphabet. It is possible for a state to have no incoming edges. There are machines for which it is not necessary to give the states specific names. For example, the FA we have been dealing with so far can be represented simply as :
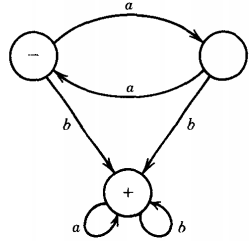
Notice that some states are neither - nor +. Even though we do not have names for the states, we can still determine whether a particular input string is accepted by this machine.
We start at the minus sign and proceed along the indicated edges until we are out of input letters.
If we are then at a plus sign, we accept the word; if not, we reject it as not being part of the language of the machine.
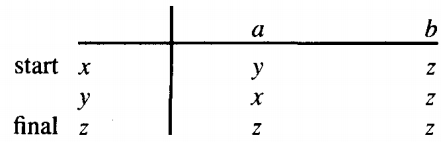
EXAMPLES OF SIMPLE FA
Q. Find the language accepted by the machine given below :
In the picture above we have drawn one edge from the state on the right back into itself and given this loop the two labels a and b, separated by a comma meaning that this is the path traveled if either letter is read.
(We save ourselves from drawing a second loop edge.)
At first glance it looks as if this machine accepts everything. The first letter of the input takes us to the right-hand state and, once there, we are trapped forever.
When the input string runs out, there we are in the correct final state. This description, however, omits the possibility that the input is the null string Λ.
If the input string is the null string, we are left back at the left-hand state, and we never get to the final state. There is a small problem about understanding how it is possible for Λ ever to be an input string to an FA, since a string, by definition, is executed (run) by reading its letters one at a time. By convention we shall say that Λ starts in the start state and then ends right there on all FA's.
The language accepted by this machine is the set of all strings except Λ. This has the regular expression definitions = (a + b)(a + b)* = (a + b)+
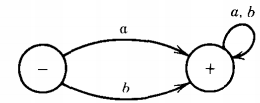
Q. Find the language accepted by the machine given below :

One of the many FA's that accepts all words is: a, b Here the sign ± means that the same state is both a start and a final state.
Since there is only one state and no matter what happens we must stay there, the language for this machine is: (a + b)*
Q. Find the language accepted by the machine given below :
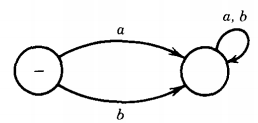
Similarly, there are FA's that accept no language. These are of two types: FA's that have no final states, such as above.
Q. Find the language accepted by the machine given below :
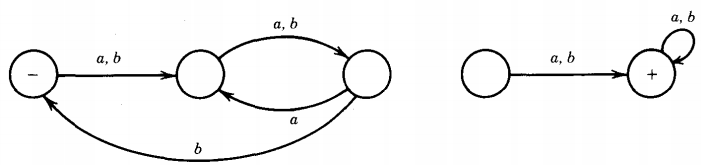
FA's in which the circles that represent the final states cannot be reached from the start state. This may be either because the above picture is in two separate components.
Q. Find the language accepted by the machine given below :
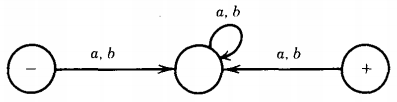
FA's in which the circles that represent the final states cannot be reached from the start state as there is no transition to the final state.
Q. Find the language accepted by the machine given below :
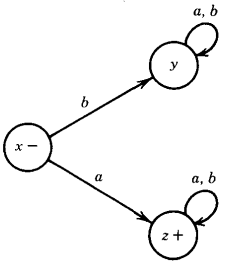
Suppose we want to build a finite automaton that accepts all the words in the language : a(a + b)*
That is, all the strings that begin with the letter a. We start at state x and, if the first letter read is a b we go to a dead-end state y. (A "dead-end state" is an informal way of describing a state that no string can leave once it has entered.)
If the first letter is an a we go to the dead-end state z, where z is a final state. The machine looks like above.
Q. Find the language accepted by the machine given below :
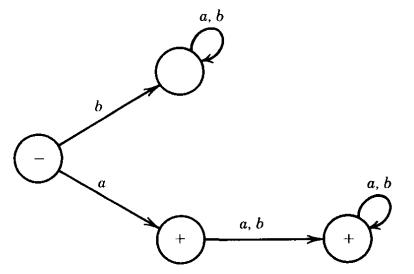
Suppose we want to build a finite automaton that accepts all the words in the language a(a + b)*.
The same language may be accepted by a four-state machine, as given above.
Only the word 'a' ends in the first + state. All other words starting with an 'a' reach and finish in the second + state where they are accepted.
Q. Find the language accepted by the machine given below :
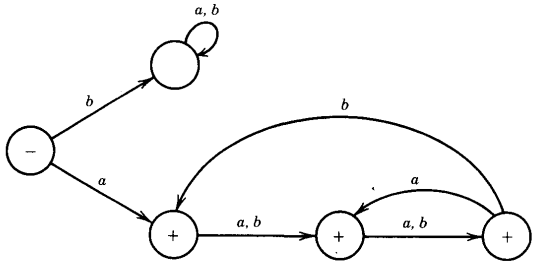
Once again Suppose we want to build a finite automaton that accepts all the words in the language a(a + b)*.
This idea can be carried further to a five-state FA as below:
The examples above are FA's that have more than one final state.
From them we can see that there is not a unique machine for a given language.
We may then ask the question, "Is there always at least one FA that accepts each possible language? More precisely, if L is some language, is there necessarily a machine of this type that accepts exactly the inputs in L, while rejecting all others?"
We shall see shortly that this question is related to the question, "Can all languages be represented by regular expressions?" We prove, that every language that can be accepted by an FA can be defined by a regular expression and, conversely, every language that can be defined by a regular expression can be accepted by some FA.
However, we shall see that there are languages that are neither definable by a regular expression nor accepted by an FA.
Remember, for a language to be the language accepted by an FA means not only that all the words in the language run to final states but also that no strings not in the language do.
Q. Find the language accepted by the machine given below :
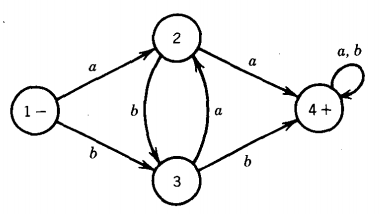
Before we begin to examine what language this machine accepts, let us trace the paths associated with some specific input strings.
Let us input the string ababa. We begin at the start state 1.
The first letter is an a, so it takes us to state 2.
From there the next letter, b, takes us to state 3. The next letter, a, then takes us back to state 2.
The fourth letter is a b and that takes us to state 3 again.
The last letter is an a that returns us to state 2 where we end. State 2 is not a final state (no +), so this word is not accepted.
Let us trace the word babbb. As always, we start in state 1.
The first letter b takes us to state 3.
An a then takes us to state 2. The third letter b takes us back to state 3.
Now another b takes us to state 4. Once in state 4, we cannot get out no matter what the rest of the string is.
Once in state 4 we must stay in state 4, and since that is the final state the string is accepted. There are two ways to get to state 4 in this FA.
One is from state 2, and the other is from state 3.
The only way to get to state 2 is by reading the input letter a (either while .in state 1 or in state 3).
So when we are in state 2 we know we have just. read an a.
If we read another a immediately, we go straight to state 4. Similarly with state 3. To get to state 3 we need to read a b.
Once in state 3, if we read another b immediately, we go to state 4; otherwise, we go to state 2.
Whenever we encounter the substring aa in an input string the first a must take us to state 4 or state 2.
Either way, the next a takes us to state 4. The situation with bb is analogous.
In summary, the words accepted by this machine are exactly those strings that have a double letter in them.
This language, as we have seen, can also be defined by the regular expression (a + b)*(aa + bb)(a + b)*
Q. Find the language accepted by the machine given below :
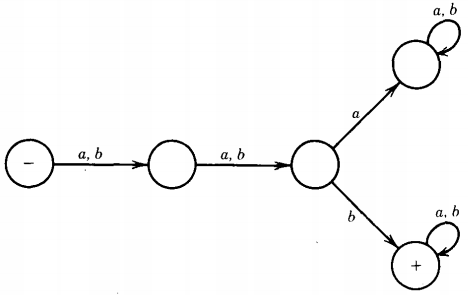
This machine will accept all words with b as the third letter and reject all other words.
The first couple of states are only waiting states eating up the first two letters of input.
Then comes the decision state. A word that has fewer than three letters cannot qualify, and its path ends in one of the three lefthand states, none of which is designated +.
Some regular expressions that define this set are
= (aab + abb + bab + bbb)(a + b)*
= (a + b)(a + b)(b)(a + b)*
= (a + b)2b (a + b)*
Notice that this last formula is not strictly speaking a regular expression, since it uses the symbol "2," which is not included in the kit.
Q. Find the language accepted by the machine given below :
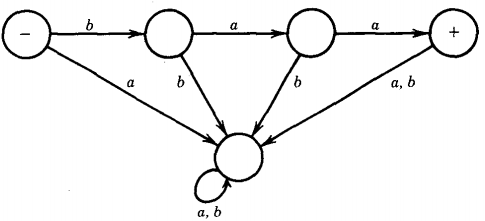
Consider a very specialized FA, one that accepts only the word baa.
Starting at the start state, anything but the sequence baa will drop down into the collecting bucket at the bottom, never to be seen again.
Even the word baabb will fail.
It will reach the final state marked with a + but then the next letter will suicide over the edge.
The language accepted by this FA is
L = {baa}
Q. Find the language accepted by the machine given below :
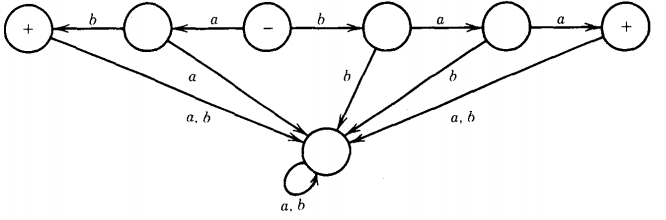
The FA above accepts exactly the two strings baa and ab.
Q. Find the language accepted by the machine given below :
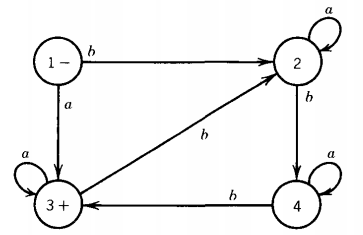
What is the language accepted by this machine? We start at state 1, and if we are reading a word starting with an a we go straight to the final state 3.
We can stay at state 3 as long as we continue to read only a's. Therefore, all words of the form = aa*
These are accepted by this machine. What if we began with some a's that take us to state 3 but then we read a b?
This then transports us to state 2. To get back to the final state, we must proceed to state 4 and then to state 3.
These trips require two more b's to be read as input.
Notice that in states 2, 3, and 4 all a's that are read are ignored.
Only b's cause a change of state. Recapitulating what we know:
If an input string begins with an a and then has some b's, it must have three b's to return us to state 3, or six b's to make the trip (state 2, state 4, state 3) twice, or 9 b's or 12 b's . ... In other words, an input string starting with an a and having a total number of b's divisible by 3 will be accepted.
If it starts with an a and has a total number of b's not divisible by 3, then the input is rejected because its path through the machine ends at state 2 or state 4.
What happens to an input string that begins with a b? It finds itself in state 2 and needs two more b's to get to state 3 (these b's can be separated by any number of a's).
Once in state 3, it needs no more b's, or three more b's, or six more b's, and so on.
All and all, an input string, whether beginning with an a or a b must have a total number of b's divisible by 3 to be accepted.
It is also clear that any string meeting this requirement will reach the final state.
The language accepted by this machine can be defined by the regular expression a*(a*ba*ba*ba*)*(a + a*ba*ba*ba*)
The only purpose for the last factor is to guarantee that Λ is not a possibility since it is not accepted by the machine.
If we did not mind Λ being included in the language
Q. Find the language accepted by the machine given below :
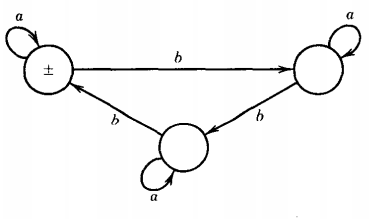
The regular expression (a + ba*ba*b)+ also defines the original (non-Λ) language
Q. Find the language accepted by the machine given below :
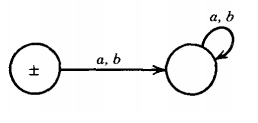
The above FA accepts only the word Λ. Notice that the left state is both a start and a final state. All words other than Λ go to the right state and stay there.
Q. Find the language accepted by the machine given below :
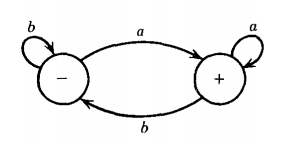
No matter which state we are in, when we read an a we go to the righthand state and when are read a b we go to the left-hand state. Any input string that ends in the + state must end in the letter a, and any string ending in a must end in +. Therefore, the language accepted by this machine is (a + b)*a
Q. Find the language accepted by the machine given below :
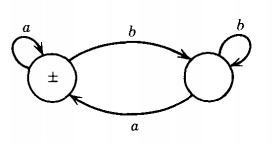
The language in the example above does not include Λ. If we add Λ we get the language of all words that do not end in b. This is accepted by the FA below.
Q. Find the language accepted by the machine given below :
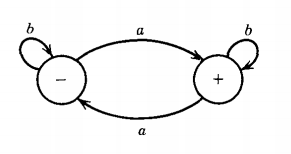
The only letter that causes motion between the states is a, b's leave the machine in the same state. We start at -. If we read a first a, we go to +. A second a takes us back. A third a takes us to + again. We end at + after the first, third, fifth, seventh, . . . a. The language accepted by this machine is all words with an odd number of a's.b*a(b*ab*ab*)*
Q. Find the language accepted by the machine given below :
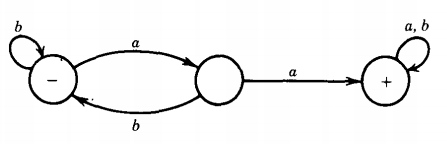
This machine will accept the language of all words with a double a in them somewhere.
We stay in the start state until we read our first a. This moves us to the middle state.
If the very next letter is another a, we move to the + state where we must stay and be accepted.
If the next letter is a b, however, we go back to - to wait for the next a.
An a followed by a b will take us from - to middle to -, while an a followed by an a will take us from - to middle to +.
The language accepted by this machine can also be defined by the regular expression
(a + b)*aa(a + b)*
Q. Find the language accepted by the machine given below :
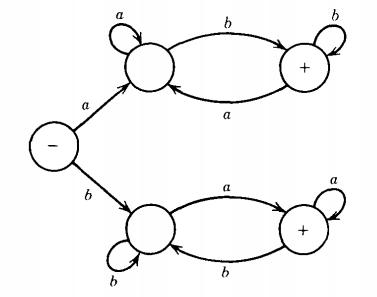
The above FA accepts all words that have different first and last letters.
If the word begins with an a, to be accepted it must end with a b and vice versa.
If we start with an a, we take the high road and jump back and forth between the two top states ending on the right (at + ) only if the last letter read is a b.
If the first letter read is a b, we get to the + on the bottom only when we read a as the last letter.
Q. Find the language accepted by the machine given below :
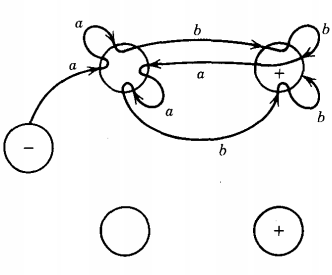
This can be better understood by examining the path through the FA of the input string aabbaabb, as shown above.
Q. Find the language accepted by the machine given below :
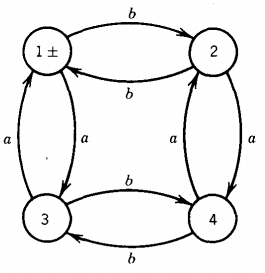
To process a string of letters, we start at state 1, which is in the upper left of the picture.
Every time we encounter a letter a in the input string we take an a train. There are four edges labeled a.
All the edges marked a go either from one of the upper two states (state 1 and state 2) to one of the lower two states (state 3 and state 4) or else from one of the lower two states to one of the upper two states.
If we are north and we read an a, we go south. If we are south and we read an a, we go north. The letter a reverses our up/down status.
What happens to a word that gets accepted and ends up back in state 1? Without knowing anything else about the string, we can say that it must have had an even number of a's in it.
Every a that took us south was balanced by some a that took us back north. We crossed the line an even number of times, one for each a.
So every word in the language of this FA has an even number of a's in it. Also, we can say that every input string with an even number of a's will finish its path in the north (state 1 or state 2).
There is more that we can say about the words that are accepted by this machine. There are four edges labeled b.
Every edge labeled b either takes us from one of the two states on the left of the picture (state 1 and state 3) to one of the two states on the right (state 2 and state 4) or else it takes us from one of the two states on the right to one of the two states on the left.
Every b we encounter in the input is an east/west reverser. If the word starts out in state 1, which is on the left, and ends up back in state 1 (on the left), it must have crossed the Mississippi an even number of times.
Therefore, all the words in the language accepted by this FA have an even number of b's as well as an even number of a's.
We can also say that every input string with an even number of b's will leave us in the west (state 1 or state 3). These are the only two conditions on the language.
All words with an even number of a's and an even number of b's must return to state 1. All words that return to state I are in EVEN-EVEN. All words that end in state 2 have crossed the line an even number of times but have crossed the Mississippi an odd number of times; therefore they have an even number of a's and an odd number of b's.
All the words that end in state 3 have an even number of b's but an odd number of a's. All words that end in state 4 have an odd number of a's and an odd number of b's.
So again we see that all the EVEN-EVEN words must end in state I and be accepted. One regular expression for the language EVEN-EVEN was discussed in detail in the previous chapter.
Notice how much 'easier it is to understand the FA than the regular expression. Both methods of defining languages have advantages, depending on the desired application.