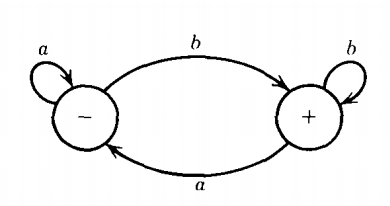
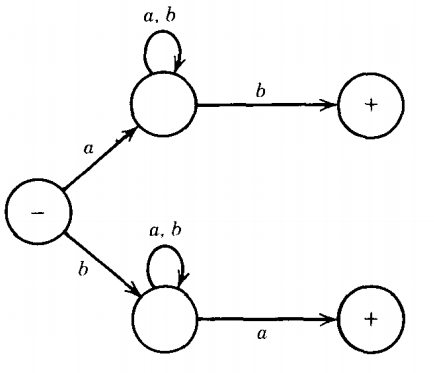
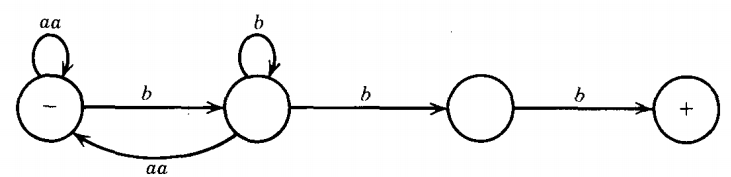
Q. language is (a + b)*b and an FA that accepts the same language is:

Q. TG that accepts the language of all words that begin and end with different letters.

Q. TG accepts the language of all words in which the a's occur only in even clumps and that end in three or more b's.

Q. Consider the following TG:

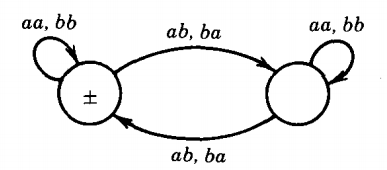
In this TG every edge is labeled with a pair of letters.

This means that for the string to be accepted it must have an even number of letters that are read in and processed in groups of two's.

Let us call the left state the balanced state and the right state the unbalanced state.

If the first pair of letters that we read from the input string is a double (aa or bb), then the machine stays in the balanced state.

In the balanced state the machine has read an even number of a's and an even number of b's.

However, when a pair of unmatched letters is read (either ab or ba), the machine flips over to the unbalanced state which signifies that it has read an odd number of a's and an odd number of b's.

We do not return to the balanced state until another "corresponding" unmatched pair is read (not necessarily the same unmatched pair, any unequal pair).

The discovery of two unequal pairs makes the total number of a's and the total number of b's read from the input string even again.

This TG is an example of a machine that accepts exactly the old and very familiar language EVEN-EVEN of all words with an even number of a's and an even number of b's.

Of the three examples of definitions or descriptions of this language we have had (the regular expression, the FA, and the TG); this last is the most understandable.

There is a practical problem with TG's. There are occasionally so many possible ways of grouping the letters of the input string that we must examine many possibilities before we know whether a given string is accepted or rejected.

Q. Consider this TG:

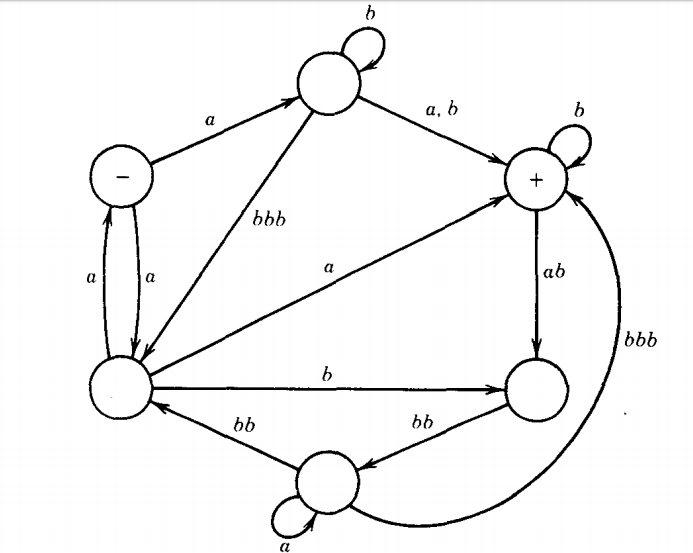
Is the word abbbabbbabba accepted by this machine? (Yes, in two ways.)

So far we saw three separate ways of defining a language: by regular expression, by finite automaton, and by transition graph.

A theorem proved by Kleene in 1956, which says that if a language can be- defined by any one of these three ways, then it can also be defined by the other two.

One way of stating this is to say that all three of these methods of defining languages are equivalent.

The three sections of our proof will be:

Part 1 Every language that can be defined by a finite automaton can also be defined by a transition graph. Every finite automaton is itself a transition graph. Therefore, any language that has been defined by a finite automaton has already been defined by a transition graph.

Part 2 Every language that can be defined by a transition graph can also be defined by a regular expression.

Part 3 Every language that can be defined by a regular expression can also be defined by a finite automaton.

Let us start by considering an abstract transition graph T. T may have many start states.

We first want to simplify T so that it has only one start state. We do this by introducing a new state that we label with a minus sign and that we connect to all the previous start states by edges labeled with the string Λ.

Then we drop the minus signs from the previous start states. Now all words must begin at the new unique start state. From there, they can proceed free of charge to any of the old start states.

If the word w used to be accepted by starting at previous start state 3 and proceeding through the machine to a final state, it can now be accepted by starting at the new unique start state and progressing to the old start state 3 along the edge labeled Λ.

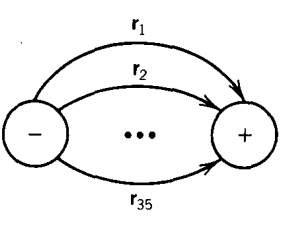
This trip does not use up any of the input letters. The word then picks up its old path and becomes accepted. This process is illustrated below on a TG that has three start states: 1, 3, and 5.

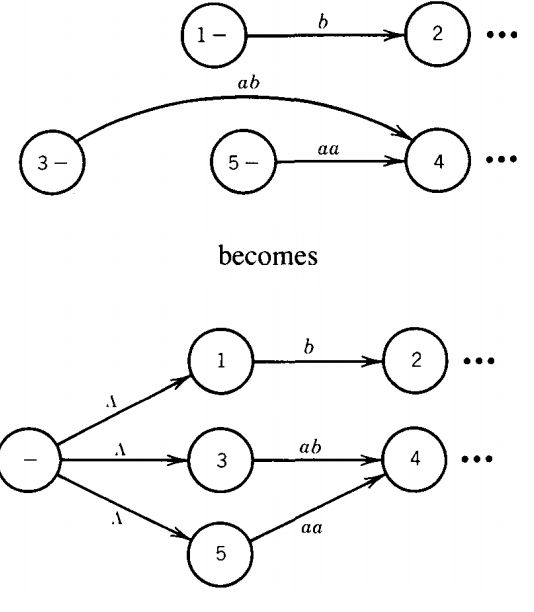
The ellipses in the pictures above indicate other, but irrelevant, sections of the TG.

Another simplification we can make in T is that it can be modified to have a unique final state without changing the language it accepts.

(If T had no final states to begin with, then it accepts no strings at all and has no language and we need produce no regular expression.)

If T has several final states, let us introduce a new unique final state labeled with a plus sign.

We draw new edges from all the old final states to the new one, drop the old plus signs, and label each new edge with the null string Λ.

We have a free ride from each old final state to the new unique final state. This process is depicted below.

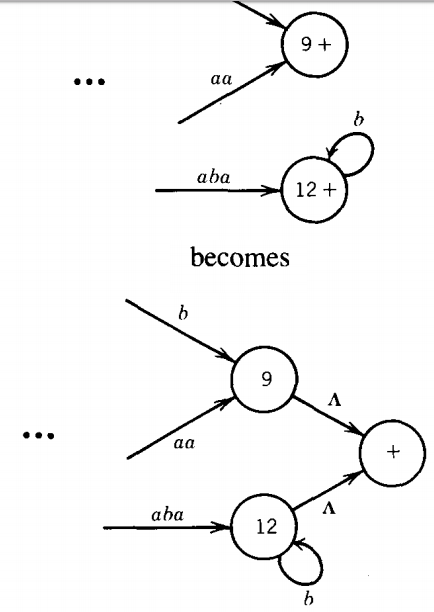
We shall require that the unique final state be a different state from the unique start state.

It should be clear that the addition of these two new states does not affect the language that T accepts. Any word accepted by the old T is also accepted by the new T, and any word rejected by the old T is also rejected by the new T.

We are now going to build the regular expression that defines the same language as T piece by piece.

To do so we extend our notion of transition graph. We previously allowed the edges to be labeled only with strings of alphabet letters.

For the purposes of this algorithm, we allow the edges to be labeled with regular expressions.

This will mean that we can travel along an edge if we read from the input string any substring that is a word in the language defined by the regular expression labeling that edge.

For example, if an edge is labeled (a + baa) as below,

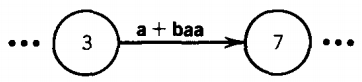
we can cross from state 3 to state 7 by reading from the input string either the letter a alone or else the sequence baa.

The ellipses on each side of the picture in this example indicate that there is more transition graph on each side of the edge, but we are focusing close up on this edge alone.

Labeling an edge with the regular expression (ab)* means that we can cross the edge by reading any of the input sequences = {Λ, ab, abab, ababab . . .}

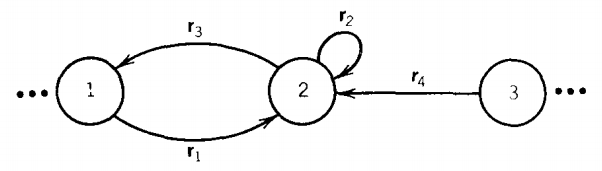
Let us suppose that T has some state (called state x) inside it (not the - or + state) that has more than one loop circling back to itself,

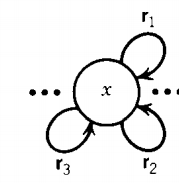
where r1, r2, and r3 are all regular expressions or simple strings. In this case, we can replace the three loops by one loop labeled with a regular expression.

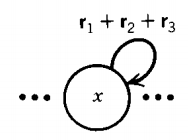
The meaning here is that from state x we can read any string from the input that fits the regular expression r1 + r2 + r3 and return to the same state.

Similarly, suppose two states are connected by more than one edge going in the same direction:

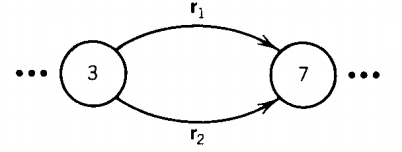
where the labels r1 and r2 are each regular expressions or simple strings. We can replace this with a single edge that is labeled with a regular expression.

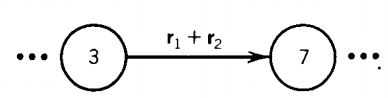
we can eliminate the middleman and go directly from one outer state to the other by a new edge labeled with a regular expression that is the concatenation of the two previous labels.

For example, if we have:

we can replace this with:

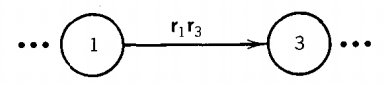
We say "replace," because we no longer need to keep the old edges from state 1 to state 2 and state 2 to state 3 unless they are used in paths other than the ones from state 1 to state 3.

The elimination of edges is our goal. We can do this trick only as long as state 2 does not have a loop going back to itself.

If state 2 does have a loop, we must use this model:

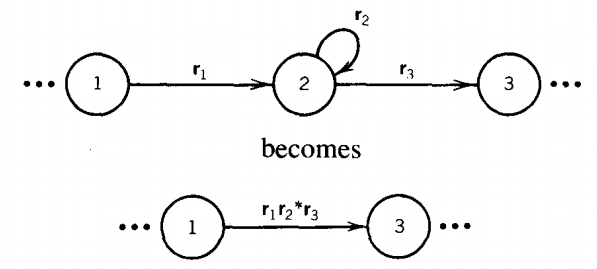
We have had to introduce the * because once we are at state 2 we can loop the loop edge as many times as we want, or no times at all, before proceeding to state 3.

Any string that fits the description r1r2*r3 corresponds to a path from state 1 to state 3 in either picture.

The Kleene star and the option of looping indefinitely correspond perfectly.

If state 1 is connected to state 2 and state 2 is connected to more than one other state (say to states 3, 4, and 5) , then when we eliminate the edge from state 1 to state 2 we have to add edges that show how to go from state 1 to states 3, 4, and 5. We do this as in the pictures below.

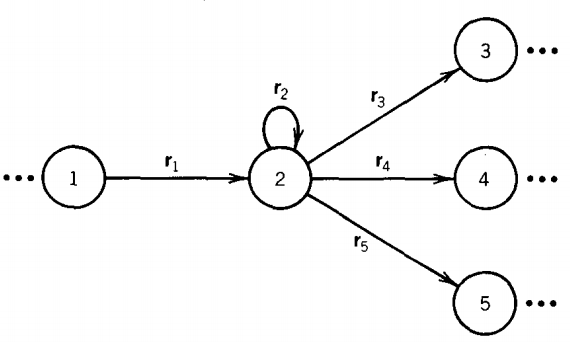
becomes

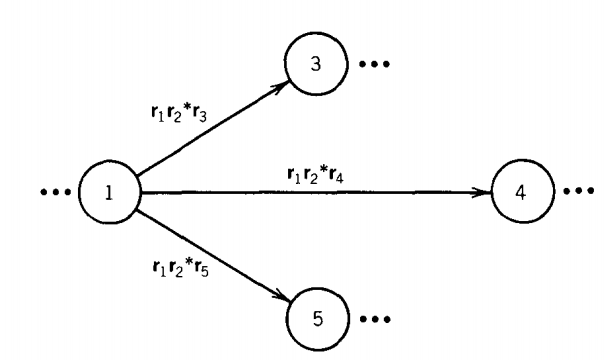
We see that in this way we can eliminate the edge from state 1 to state 2, bypassing state 2 altogether.

In fact, every state that leads into state 2 can be made to bypass state 2. If state 9 leads into state 2, we can eliminate the edge from state 9 to state 2 by adding edges from state 9 to states 3, 4, and 5 directly.

We can repeat this process until nothing leads into state 2. When this happens, we can eliminate state 2 entirely, since it then cannot be in a path that accepts a word.

We drop it, and the edges leading from it, from the picture for T. What have we done to transition graph T? Without changing the set of words that it accepts, we have eliminated one of its states.

We can repeat this process again and again until we have eliminated all the states from T except for the unique start state and the unique final state. (We shall illustrate this presently.)

What we come down to is a picture that looks like this:

with each edge labeled by a regular expression. We can then combine this once more to produce:

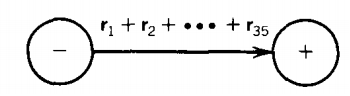
The resultant regular expression, is then the regular expression that defines the same language T did originally . For example, if we have:

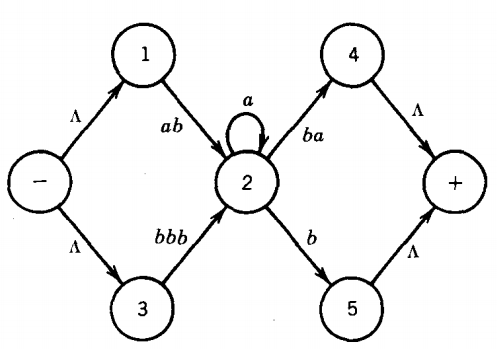
we can bypass state 2 by including a path from state 1 to state 4 labeled aba*ba , a path from state 1 to state 5 labeled aba*b, a path from state 3 to state 4 labeled bbba*ba, and a path from state 3 to state 5 labeled bbba*b.

We can then erase the edges from state 1 to state 2 and from state 3 to state 2. Without these edges, state 2 becomes unreachable.

The edges from state 2 to states 4 and 5 are then useless because they cannot be part of any path from - to +.

Dropping this state and these edges will not affect whether any word is accepted by this TG. The machine that results from this operation is:

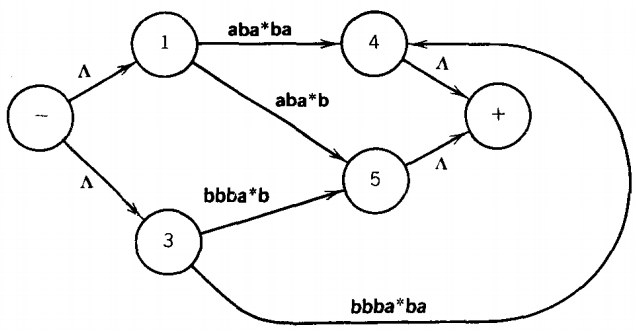
Before we claim to have finished describing this algorithm, there are some special cases that we must examine more carefully. In this picture

we might want to eliminate the edge from state 1 to state 2. Since state 2 goes nowhere except into state 1 , we might think that we can rewrite this part of T as

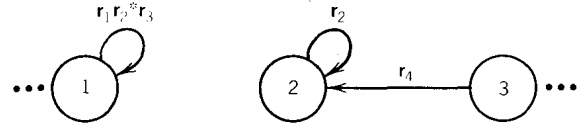
but this is wrong. In the original picture, we could go from state 3 to state 1 , while in the modified picture that is impossible. Therefore, we must introduce an edge from state 3 to state 1 and label it as below.

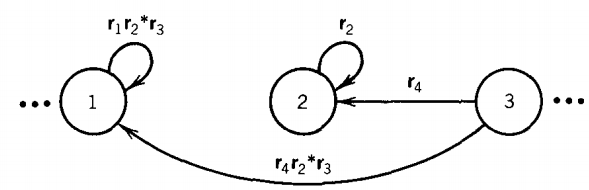
Whenever we remove an edge or a state we must be sure that we have not destroyed any paths through T that may previously have existed.

Destroying paths could change the language of words accepted , which we do not want to do. Since there are only finitely many paths in the whole TG (not counting looping and repeating circuits), we can check this possibility in a finite number of steps.

This example is symptomatic of the only problem that arises with this algorithm, so we now have a well-described method of producing regular expressions equivalent to given transition graphs.

All words accepted by T are paths through the picture of T. If we change the picture but preserve all paths and their labels, we must keep the language unchanged.

This algorithm terminates in a finite number of steps, since T has only finitely many states to begin with, and one state is eliminated with each iteration. The other important observation is that the method works on all transition graphs.

Therefore, this algorithm provides a satisfactory proof that there is a regular expression for each transition graph. Before proceeding to the proof of Part 3, let us illustrate the algorithm above on a particular example.

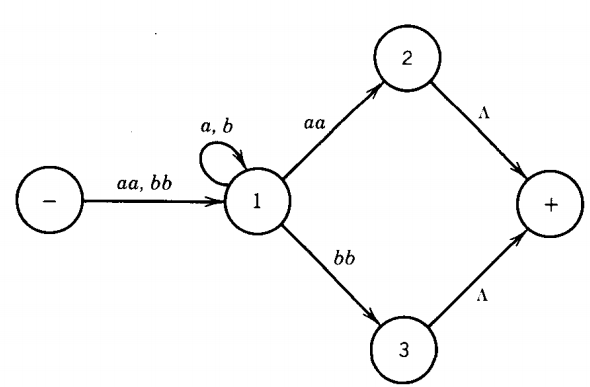
The TG we shall consider is the one below, which accepts all words that begin and end with double letters (having at least four different letters). This is by no means the only TG that accepts this language.

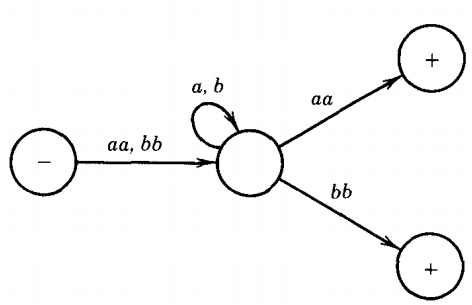
As it stands, this machine has only one start state, but it has two final states, so we must introduce a new unique final state following the method prescribed by the algorithm.

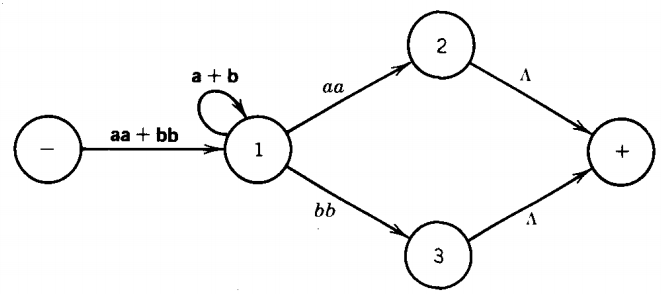
The next modification we perform is to note that the edge from the start state to state 1 is a double edge-we can travel over it by an aa or a bb. We replace this by the regular expression aa + bb.

We also note that there is a double loop at state 1. We can loop back to state 1 on a single a or on a single b.

The algorithm says we are supposed to replace this double loop by a single loop labeled with the regular expression a + b. The picture of the machine has now become:

Let us choose for our next modification the path from state 1 to state 2 to state +. The algorithm does not actually tell us which section of the TG we must attack next.

The order is left up to our own discretion. The algorithm tells us that it really does not matter. As long as we continue to eliminate edges and states, we shall be simplifying the machine down to a single regular expression representation.

The path we are considering now is:

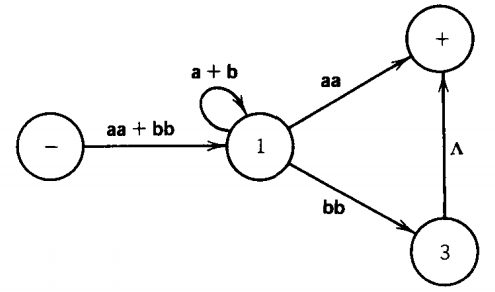
The algorithm says we can replace this with one edge from state 1 to state + that bears the label that is the concatenation of the regular expressions on the two parts of the path.

In this case, aa is concatenated with Λ, which is only aa again. Once we have eliminated the edge from state 1 we can eliminate state 2 entirely.

The machine now looks like this.

It seems reasonable now for us to do the same thing with the path that goes from state 1 to state 3 to state +.

But the algorithm does not require us to be reasonable, and since this is an illustrative example and we have already seen something like this path, we shall choose a different section of T to modify.

Let us try to bypass state 1. Only one edge comes into state 1 and that is from state -. There is a loop at state 1 with the label (a + b).

State 1 has edges coming out of it that lead to state 3 and state +.

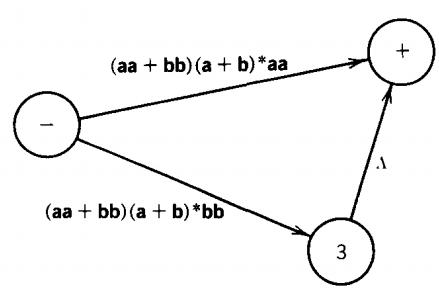
The algorithm explains that we can eliminate state 1 and replace these edges with an edge from state - to state 3 labeled (aa + bb)(a + b)*(bb) and an edge from state - to state + labeled (aa + bb)(a + b)*(aa).

The starred expression in the middle represents the fact that while we are at state 1 we can loop around as long as we want-ten times, two times or even no times.

It is no accident that the definition of the closure operator * exactly corresponds to the situation of looping, since Kleene invented it for this very purpose. After eliminating state 1, the machine looks like this:

When we concatenate the regular expression from state - to state 3 with the regular expression from state 3 to state +, we are left with the machine:

(aa + bb)(a + b)*(aa) + (aa + bb)(a + b)*(bb)

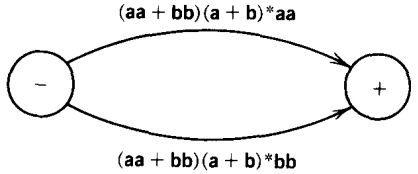
If we had to make up a regular expression for the language of all strings that begin and end with double letters, we would probably write: (aa + bb)(a + b)*(aa + bb)

which is equivalent to the regular expression that the algorithm produced because the algebraic distributive law applies to regular expressions.

Without going through lengthy descriptions, let us watch the algorithm work on one more example. Let us start with the TG that accepts strings with an even number of a's and an even number of b's, the language EVEN-EVEN.

(We keep harping on these strings not because they are so terribly important, but because it is the hardest example we thoroughly understand, and rather than introduce new hard examples we keep it as an old conquest.)

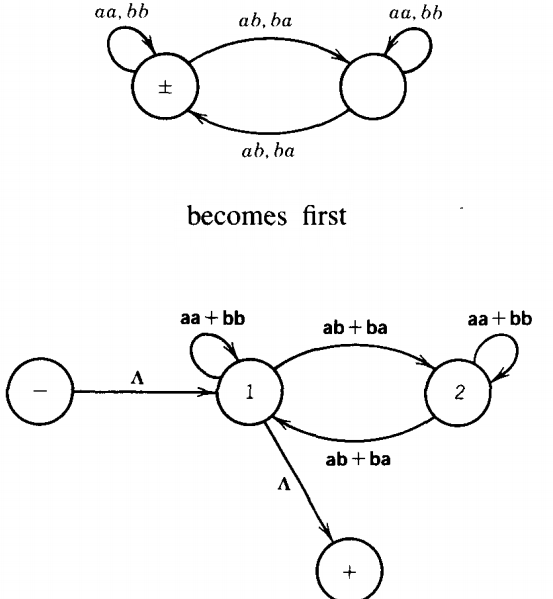
When we eliminate state 2, the path from 1 to 2 to 1 becomes a loop at state 1:

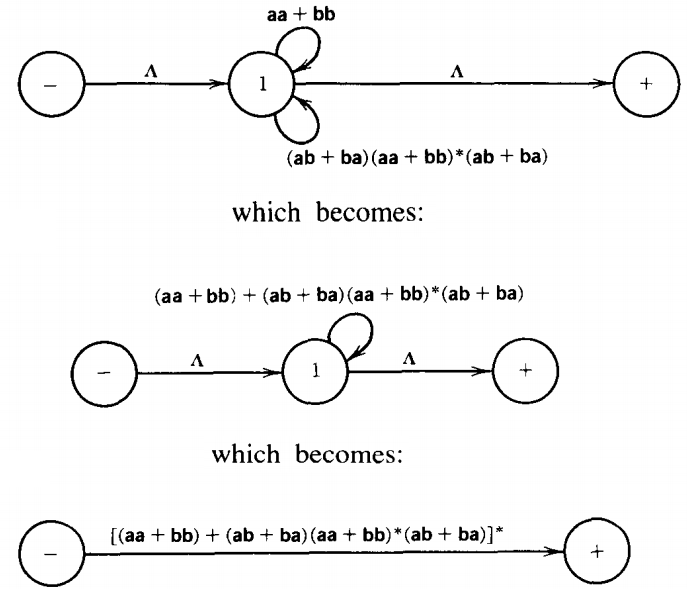
which reduces to the regular expression: Σ(aa + bb) + (ab + ba)(aa + bb)*(ab + ba)]*

which is exactly the regular expression we used to define this language before.

We still have one part of Kleene's theorem yet to prove. We must show that for each regular expression we can build a finite automaton that accepts the same language.

We know that every regular expression can be built up from the letters of the alphabet and Λ by repeated application of certain rules: addition, concatenation, and closure.

We shall see that as we are building up a regular expression, we could at the same time be building up an FA that accepts the same language.

We present our algorithm recursively.

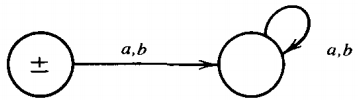
Rule 1 : There is an FA that accepts any particular letter of the alphabet. There is an FA that accepts only the word Λ.

For example: If x is in Σ, then the FA

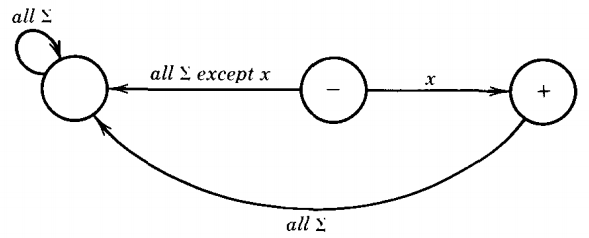
accepts only the word x. One FA that accepts only Λ is

Rule 2 If there is an FA called FA1 that accepts the language defined by the regular expression r, and there is an FA called FA2 that accepts the language defined by the regular expressions r2, then there is an FA called FA3 that accepts the language defined by the regular expression (r1 + r2).

We are going to prove this by showing how to construct the new machine in the most reasonable way.

Before we state the general principles, let us demonstrate them in a specific example. Suppose we have the machine FA1, which accepts the language of all words over the alphabet

Σ = {a, b}

that have a double a somewhere in them,

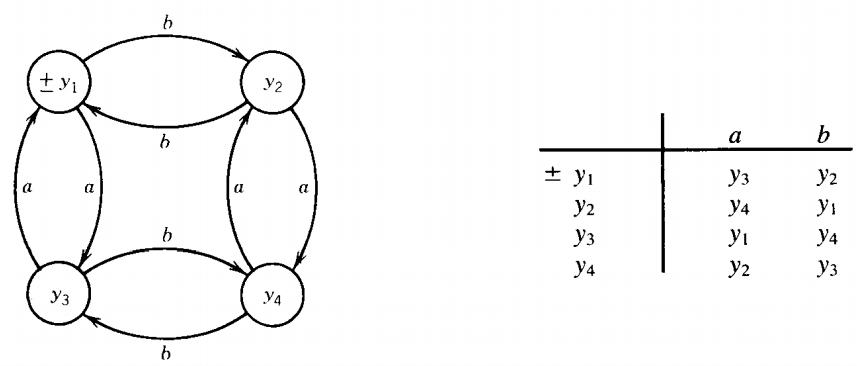
and the familiar machine FA2 , which accepts all words that have both an even number of total a's and an even number of total b's (this is the language EVEN-EVEN).

We shall show how to design a machine that accepts both sets. That is, we will build a machine that accepts all words that either have an aa or are in EVEN-EVEN and rejects all strings with neither characteristic.

The language the new machine accepts will be the union of these two languages. We shall call the states in this new machine z1, z2 , z3 , and so on, for as many as we need.

We shall define this machine by its transition table. Our guiding principle is this: The new machine will simultaneously keep track of where the input would be if it were running on FA1 and where the input would be if it were running on FA2.

First of all, we need a start state. This state must combine x1 , the start state for FA1, and y1, the start state for FA2 . We call it z1 If the string were running on FA1, it would start in x1, on FA2 in y1.

What new states can occur if the input letter a is read in? If the string were being run on the first machine, it would put the machine into state x2.

If the string were running on the second machine, it would put the machine into state Y3 .

Therefore, on our new machine an a puts us into state z2 , which means either x2 or Y3, in the same way that z, means either x, or y1. Since y, is a final state, for FA2, Z1 is also a final state in the sense that any word whose path ends there on the z-machine would be accepted by FA2.

z1= x1 or y1, z2 = x2 or y3

On the machine FA3 we are following both the path the input would make on FA1 and the path on FA2 at the same time.

By keeping track of both paths, we know when the input string ends whether or not it has reached a final state on either machine.

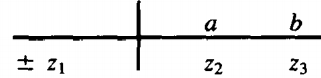
If we are in state z1, and we read the letter b, we then go to state z3, which represents either x1 or Y2. The x1 comes from being in x1 on FA, and reading a b, whereas the y2 comes from being in y2 on FA2 and reading a b.

Z3 = x1 or Y2

The beginning of our transition table for FA3 is:

Suppose that somehow we have gotten into state z2 and then we read an a.

If we were in FA1, we would now go to state x3, which is a final state. If we were in FA2, we would now go back to y1, which is also a final state.

We will call this condition z4 , meaning either x3 or y1. Since this string could now be accepted on one of these two machines, z4 is a final state for FA3.

As it turns out, in this example the word is accepted by both machines at once, but this is not necessary. Acceptance by either machine FA1 or FA2 is enough for acceptance by FA3.

If we are in state z2 and we happen to read a b, then in FA1 we are back to x, whereas in FA2 we are in Y4. Call this new condition z5 = state x1 or Y4.

+ Z4 = X3 or y1 ; Z5 = x1 or y4

At this point our transition table looks like this:

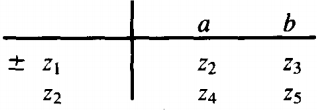
What happens if we start from state z3 and read an a? If we were in FA1, we are now in x2, if in FA2, we are now in Y4. This is a new state; call it state z6.

Z6 = X2 or y4

What if we are in z3 and we read a b? In FA1 we stay in x1 , whereas in FA2 we return to y1. This means that if we are in z3 and we read a b we return to state z1. Our transition table now looks like this:

What if we are in z4 and we read an a? FA1 remains in x3, whereas FA2 goes to Y3 . This is a new state; call it z7.

If we are in z4 and we read a b, the FA1 part stays at x3 whereas the FA2 part goes to Y2. This is also a new state; call it z8.

+ z7 = x3 or y3 + z8 = x3 or Y2

Both of these are final states because a string ending here on the z-machine will be accepted by FA1, since x3 is a final state for FA1 .

If we are in z5 and we read an a, we go to x2 or Y2, which we shall call Z9 .

If we are in z5 and we read a b, we go to x, or Y3, which we shall call z10

Z9 = x2 or Y2 z10= x1 or Y3

If we are in Z6 and we read an a, we go to x3 or Y2, which is our old Z8.

If we are in z6 and we read a b, we go to x, or Y3, which is z10 again.

If we are in z7 and we read an a we go to x3 or yi, which is z4 again.

If we are in z7 and we read a b, we go to x3 or Y4, which is a new state, Z11.

+ Z11 = X3 or Y4

If we are in z8 and we read an a, we go to x3 or Y4 = z11 . If in z8 we read a b, we go to x3 or y1 = Z4

If we are in z9 and we read an a, we go to x3 or Y4 = Z11. If in z9 we read a b, we go to x1 or y1 = z1.

If we are in z10 and we read an a, we go to x2 or yl, which is our last new state, z12.

+ Z12 = x2 or y1

If we are in z10 and we read a b, we go to (x1 or y4) = z5 .

If we are in z11 and we read an a, we go to (x3 or y2)= z8.

If we are in z11 and we read a b, we go to (x3 or y3) = Z7.

If we are in z12 and we read an a, we go to (x3 or Y3) = Z7.

If we are in Z12 and we read a b, we go to (x1 or y2) = z3.

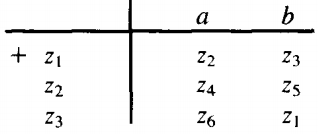
Our machine is now complete. The full transition table is:

If a string traces through this machine and ends up at a final state, it means that it would also end at a final state either on machine FA1 or on machine FA2 . Also, any string accepted by either FA1 or FA2 will be accepted by this FA3.

The general description of the algorithm we employed above is as follows. Starting with two machines, FA1 with states x1, x2, x3, . . . and FA2 with states Y1, Y2, Y3 . . ., build a new machine FA3 with states z1, z2, z3. . .. where each z is of the form "Xsomething or Ysomething".

If either the x part or the y part is a final state, then the corresponding z is a final state.

To go from one z to another by reading a letter from the input string, we see what happens to the x part and to the y part and go to the new z accordingly. We could write this as a formula:

Znew after letter p = [Xnew after letter p] or [Ynew after letter p]

Since there are only finitely many x's and y's, there can be only finitely many possible z's.

Not all of them will necessarily be used in FA3 . In this way, we can build a machine that can accept the sum of two regular expressions if there are already machines to accept each of the component regular expressions separately. Let us go through this very quickly once more on the two machines:

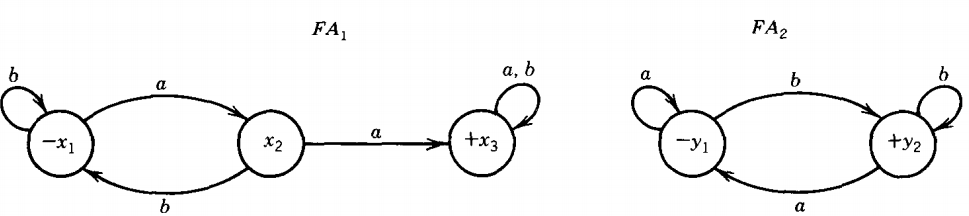
FAl accepts all words with a double a in them, and FA2 accepts all words ending in b.

The machine that accepts the union of the two languages for these two machines begins:

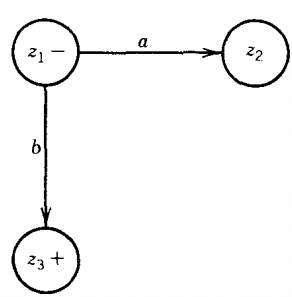
- z1 = x1 or Y1

In z1 if we read an a, we go to (X2 or Y1) = z2.

In zl, if we read a b, we go to (x1 or Y2) = z3, which is a final state since Y2 is.

The partial picture of this machine is now:

In z2 if we read an a, we go to (x3 or y1) = z4 , which is a final state because x3 is. In z2 if we read a b, we go to (x1 or Y2) = z3

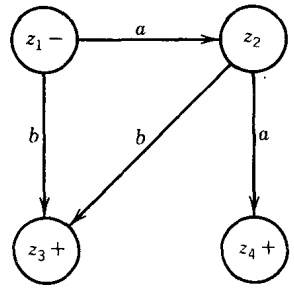
In z3 if we read an a, we go to (x2 or y1) = z2.

In z3 if we read a b, we go to (x1 or Y2) = z3.

In z4 if we read an a, we go to (x3 or y1) = z4.

In z4 if we read a b, we go to (x3 or Y2) z5 , which is a final state.

In z5 if we read an a, we go to (x3 or y1) = z4.

In z5 if we read a b, we go to x3 or Y2 = z5.

The whole machine looks like this:

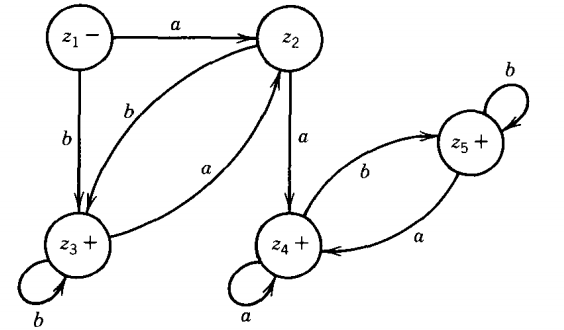
This machine accepts all words that have a double a or that end in b. The seemingly logical possibility

Z6 = (x2 or Y2)

does not arise. This is because to be in x2 on FA1 means the last letter read is an a. But to be in Y2 on FA2 means the last letter read is a b. These cannot both be true at the same time, so no input string ever has the possibility of being in state z6 .