So far, We said that we would label every edge of the graph with any string of alphabet letters (perhaps even the null string Λ). We even allowed two edges coming out of the same state to have exactly the same label:

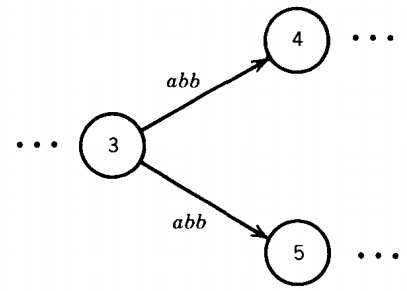
If we tried to forbid people from writing this directly, they could sneak it into TG's in other ways:

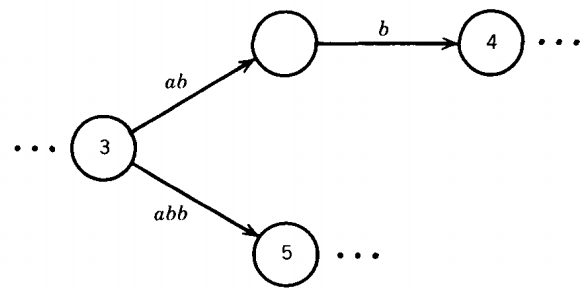
Even if we restrict labels to strings of only one letter or Λ, we may indirectly permit these two equivalent situations:

We have already seen that in a TG a particular string of input letters may trace through the machine on different paths, depending on our choice of grouping.

For instance, abb can go from state 3 to 4 or 5 in the middle example above depending on whether we read the letters two and one or all three at once.

The ultimate path through the machine is not determined by the input alone.

Therefore, we say this machine is nondeterministic. Human choice becomes a factor in selecting the path; the machine does not make all its own determinations.

Remember that a string is accepted by the machine if at least one sequence of choices leads to a path that ends at a final state.

In 1959, Michael Oser Rabin and Dana Scott introduced the notion of nondeterminism for language-recognizing finite automata.

A nondeterministic finite automaton (NFA) is a collection of three things:

Some authors argue that an NFA is not a special case of a TG since they insist in their definition that a TG is not allowed more than one edge from one state with the same label.

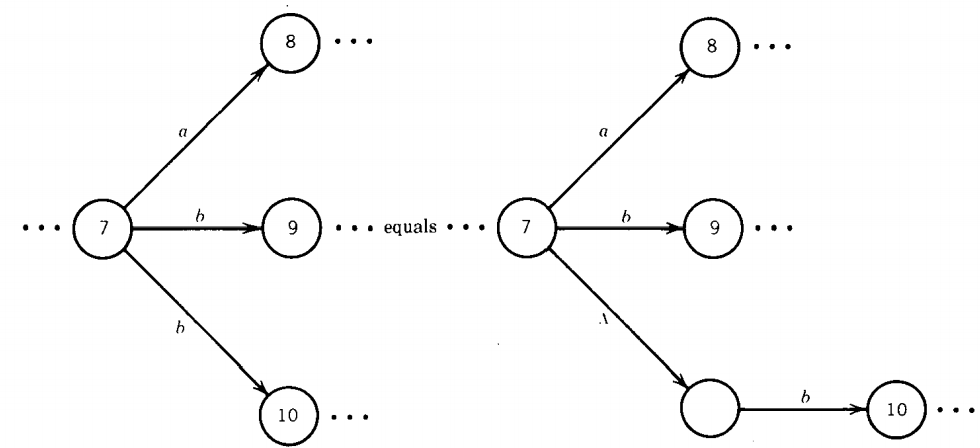
Let us observe that we can replace all same-labeled edges using this trick:

is equivalent to

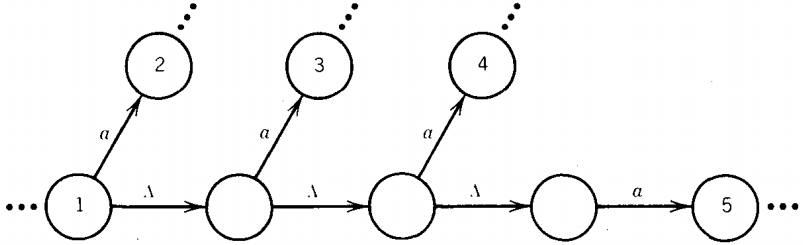
or this trick

is equivalent to

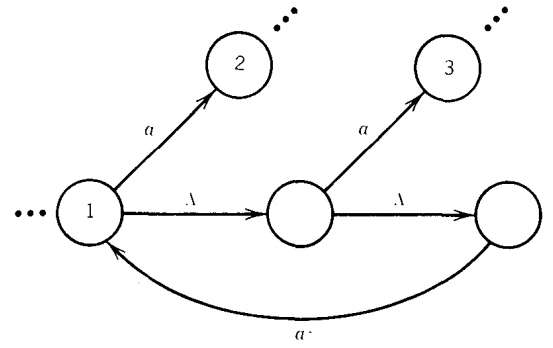
Therefore, we can convert any NFA into a TG with no repeated labels from any single state.

Let us also observe that every deterministic finite automaton can be considered as an example of an NFA where we did not make use of the extra possible features.

Nowhere in the definition of NFA did we insist that an NFA have nondeterministic branching. Any FA will satisfy the definition of an NFA.

So we have:

Therefore: languages of FA's ⊂ languages of NFA's ⊂ languages of TG's languages of FA's

by which we mean that any language definable by a nondeterministic finite automaton is also definable by a deterministic (ordinary) finite automaton and vice versa.

We say then that they are of equal power.

Let us not mistake the equation FA = NFA as meaning that every NFA is itself an FA. This is not true.

Only that for every NFA there is some FA that is equivalent to it as a language acceptor.

NFA's may sometimes be easier or more intuitive to use than FA's to define a given language.

One example of this is a machine to combine two FA's, one that accepts the language of the regular expression r1 and the other for the language of the regular expression r2.

If the start states in these two machines have no edges coming into them, we can produce an NFA3 that accepts exactly the language of r1 + r2 by amalgamating the two start states.

This is illustrated below.

Let FA1 be

And let FA2 be

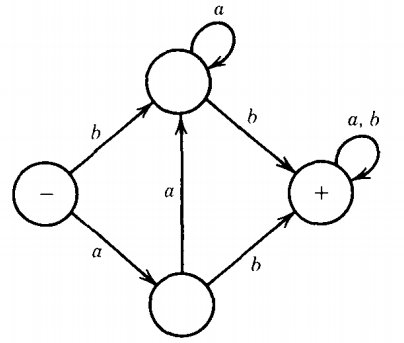
Then NFA3 = FA1 + FA2 is

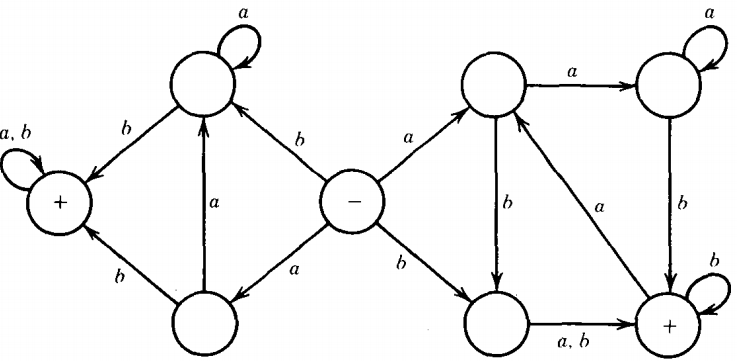
Nondeterminism does not increase the power of an FA, but we shall see that it does increase the power of the more powerful machines introduced later.

It is sometimes easier to understand what a language is from the picture of an NFA that accepts it than from the picture of an FA.

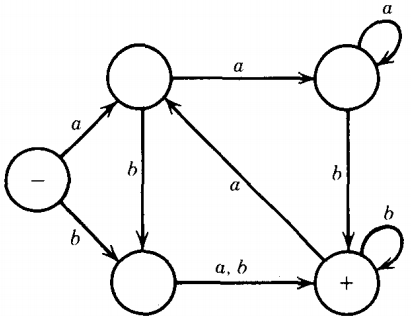
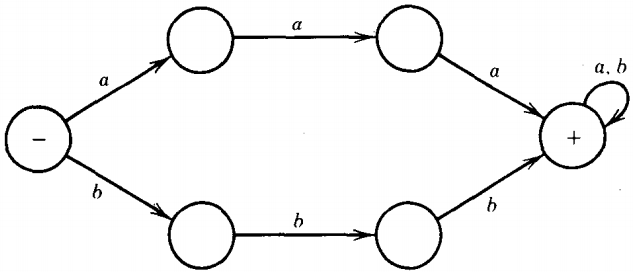
Let us take, for example, the language of all words that contain either a triple a (the substring aaa) or a triple b (the substring bbb) or both.

The NFA below does an obvious job of accepting this language.

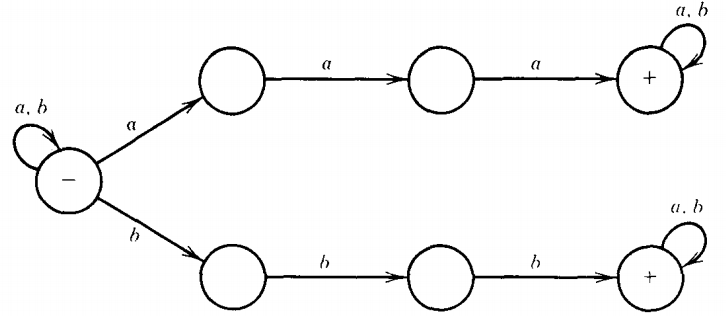
If a word contains aaa somewhere inside of it, it can be accepted by a path along the high road.

If it contains bbb, it can be accepted along the low road. If a word has both, it can use either route.

Clearly, anything that gets to + has one of these substrings.

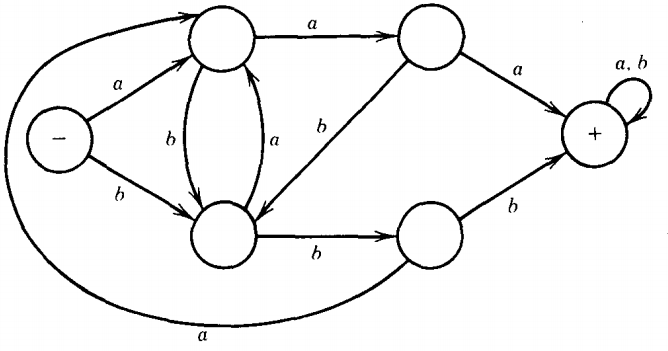
Let us now build an FA that accepts this language.

It must have a start state. From the start state, it must have a path of three edges to accept the word aaa.

It needs three edges because otherwise a shorter string of a's could be accepted. Therefore, we begin our machine with

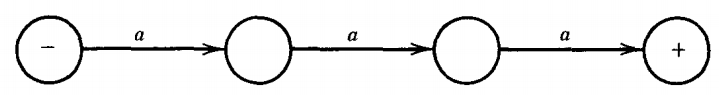
For similar reasons, we can deduce that there must be a path for bbb that has no loop and uses entirely different states.

If it shared any of the same states, we could begin with a's and pick up with b's.

So we must have at least two more states since we could share the last state of the three-edge path with one of the a states already drawn.

If we are along the a path and read a b before the third a, we jump to the beginning of the b path and vice versa. The whole FA then looks like this:

We can understand this FA because we have seen it built, but the NFA is still much easier to interpret.

Nondeterminism can have important practical applications, in particular in the subject of artificial intelligence (AI). We shall demonstrate this on one simple example.

Suppose the problem we want to solve is the maze below:

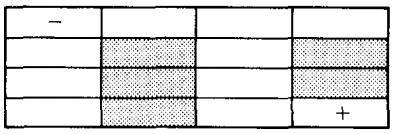
The rules are that we start at - and can proceed from square to adjacent square.

We can walk only in empty squares, the dark squares are walls. When we get to the + we stop.

This is not a very hard maze to figure out, but we are only taking an illustrative example.

Let us number the open squares as follows:

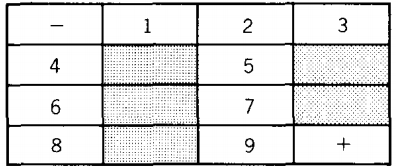
Let us build the following nondeterministic finite automaton in which every state represents a square in the maze and one state can be reached from the other in the NFA only if the same move is possible in the maze.

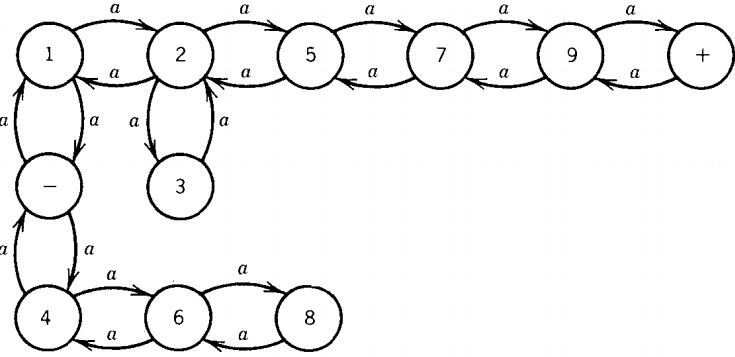
The permission for each step is the letter 'a' ? The question does this maze have a solution in six steps? is the same as the question,

"Is the word aaaaaa accepted by this NFA?"

If the language for the NFA of some other maze was {aaa, aaaaa}, that would mean that there was a solution path of three steps and one of five steps.

An algorithm that found all the words accepted by an NFA would automatically tell us all the lengths of the solution paths to all mazes. We already have such an algorithm. If we consider this NFA as a TG and apply the TG into regular expression conversion algorithm , we discover, after simplification, that the language accepted by this machine is defined by aaaaaa(aa)*, which means that there are solutions of six steps, eight steps, ten steps, and so on

With Finite automata, our motivation was in part to design a mathematical model for a computer.

We said that the input string represents the program and input data.

Reading the letters from the string is analogous to executing instructions in that it changes the state of the machine, that is, it changes the contents of memory, changes the control section of the computer, and so on.

We could consider the output as' part of the total state of the machine.

This could mean two different things: one, that to enter a specific computer state means change memory a certain way and print a specific character, or two, that a state includes both the present condition of memory plus the total output thus far.

In other words, the state could reflect what we are now printing or what we have printed in total.

One natural question to ask is, "If we have these two different models, do these machines have equal power or are there some tasks that one can do that tite other cannot?"

If we assume that all the printing of output is to be done at the end of the program run, at which time we have an instruction that dumps a buffer, then we have a maximum on the number of characters that the program can print, namely the size of the buffer.

However, theoretically we should be able to have outputs of any finite length.

For example, we might simply want to print out a copy of the input string, which could be arbitrarily long.