EXAMPLE : Convert Mealy machine to Moore machine
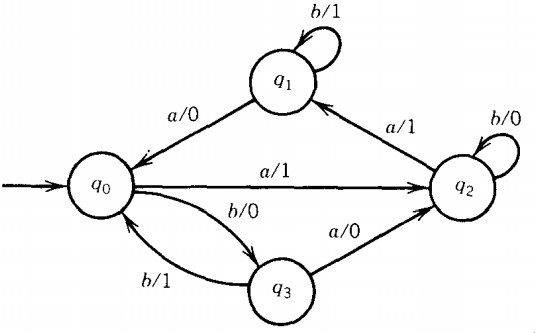
We can begin the conversion process anywhere because the algorithm does not specify the order of replacing states; so let us first consider the state qo. Two edges come into this state, one labeled a/0 and one labeled b/1.
Therefore, we need two copies of this state: one that prints a 0 (called q01) and one that will print a 1 (called q02).
Both of these states must be connected to q2 through an edge labeled a/l and to q3 through an edge labeled b/0. There is no loop at q0, so these two states are not connected to each other. The machine becomes:
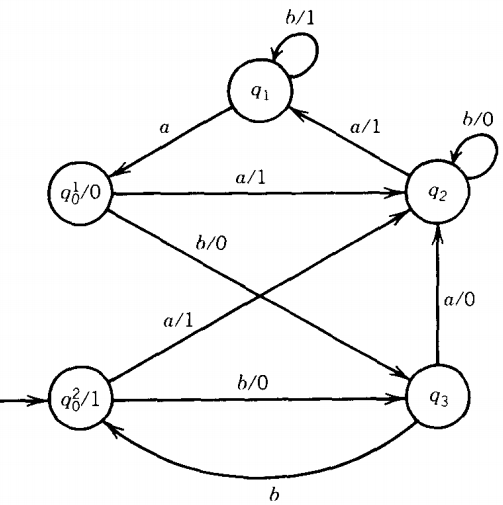
We must select the start state for the new machine, so let us arbitrarily select q02.
Notice that we now have two edges that cross. This sometimes happens, but aside from making a messier picture, there is no real problem' in understanding which edge goes where.
Notice that the edge from q1 to q0, which used to be labeled a/0, is now only labeled a because the instruction to print the 0 is found in the state q01/0.
The same is true for the edge from q3, which also loses its printing instruction.
State q1 has only two edges coming into it: one from q2 labeled a/1 and a loop labeled b/1.
So whenever we enter q1 we are always printing a 1. We have no trouble here transferring the print instructions from the edges into the state. The machine now looks like this:

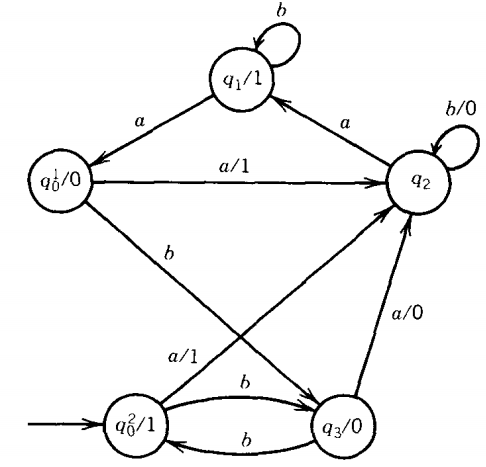
What we have now is a partially converted machine or a hybrid. We could run an input string on this machine, and it would give us the same output as the original Me.
The rules are that if an edge says print, then print; if a state says print, then print. If not, don't.
Let us continue the conversion. State q3 is easy to handle. Two edges come into it, both labeled b/0, so we change the state to q3/0 and simplify the edge labels to b alone.
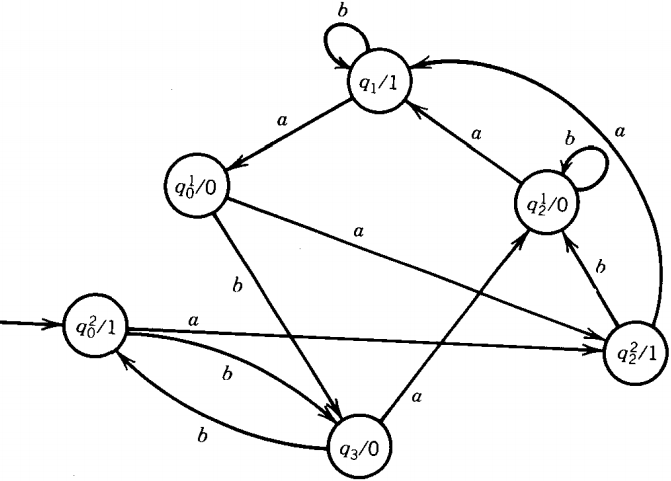
The only job left is to convert state q2. It has some 0-printing edges entering it and some 1-printing edges (actually two of each, counting the loop).
Therefore, we must split it into two copies, q21 and q22. Let the first print a 0 and the second print a 1.
The two copies will be connected by a b edge going from q22 to q21 (to print a 0). There will also be a b loop at q21. The final machine is this:
Example of a simple sequential circuit
Let us consider an example of a simple sequential circuit. The box labeled NAND means "not and."
Its output wire carries the complement of the Boolean AND of its input wires.
The output of the box labeled DELAY is the same as its previous input.
It delays transmission of the signal along the wire by one step (clock pulse). The DELAY is sometimes called a D flip-flop. The AND and OR are as usual. Current in a wire is denoted by the value 1, no current by 0.
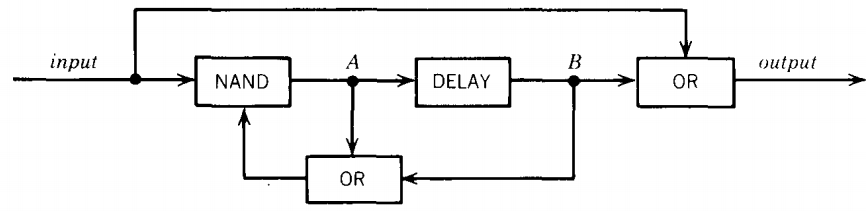
We identify four states based on whether or not there is current at points A and B in the circuit.
q0 is A = 0 B = 0
q1 is A = 0 B = 1
q2 is A = 1 B = 0
q3 is A = 1 B = 1
The operation of this circuit is such that after an input of 0 or 1 the state changes according to the following rules:
new B = old A
new A = (input) NAND (old A OR old B)
output = (input) OR (old B)
At various discrete pulses of a time clock input is received, the state changes, and output is generated.
Suppose we are in state q0 and we recive the input 0:
new B = old A = 0
new A = (input) NAND (old A OR old B)
= (0) NAND (0 OR 0)
= 0 NAND 0
= 1
output = 0 OR 0 = 0 The new state is q2 (since new A = 1, new B = 0).
If we are in state q0 and we receive the input 1:
new B = old A = 0
new A = 1 NAND (0 OR 0) = 1
output = 1 OR 0 = 1
The new state is q2 (since the new A = 1 and the new B = 0).
If we are in q, and we receive the input 0:
new B = old A = 0
new A = 0 NAND (0 OR 1) = 1
output = 0 OR 1 = 1
The new state is q2.
If we are in q1 and we receive the input 1:
new B = old A = 0
new A = 1 NAND (0 OR 1) = 0
output = 1 OR 1 = 1
The new state is q0.
If we are in state q2 and we receive the input 0:
new B = old A = 1
new A = 0 NAND (1 OR 0) = 1
output = 0 OR 0 = 0
The new state is q3 (since new A = 1, new B = 1).
If we are in q2 and we receive the input 1:
new B = old A = 1
new A = 1 NAND (1 OR 0) = 0
output = 1 OR 0 = 1
The new state is q1 .
If we are in q3 and we receive the input 0:
new B = old A = 1
new A = 0 NAND (1 OR 1) = 1
output = 0 OR 1 = 1
The new state is q3.
If we are in q3 and we receive the input 1:
new B = old A = 1
new A = 1 NAND (1 OR 1) = 0
output = 1 OR 1 = 1
The new state is q1 .
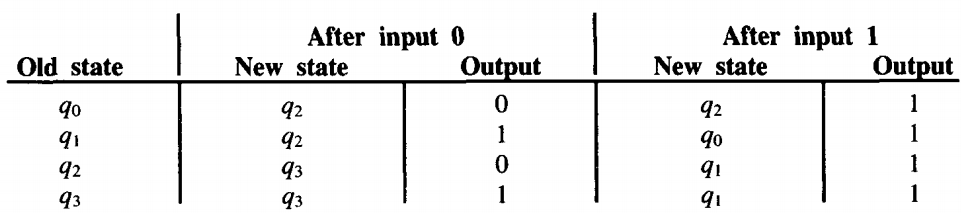
The action of this sequential feedback circuit is equivalent to the following Mealy machine.
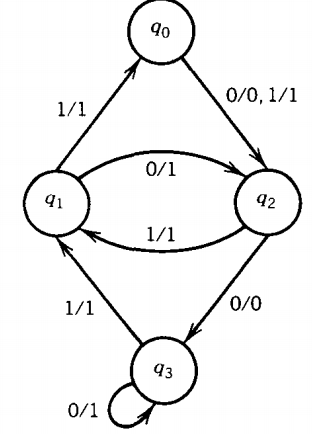
If we input two O's no matter which state we started from, we will get to state q3. From there the input string 011011 will cause the output sequence 111011.
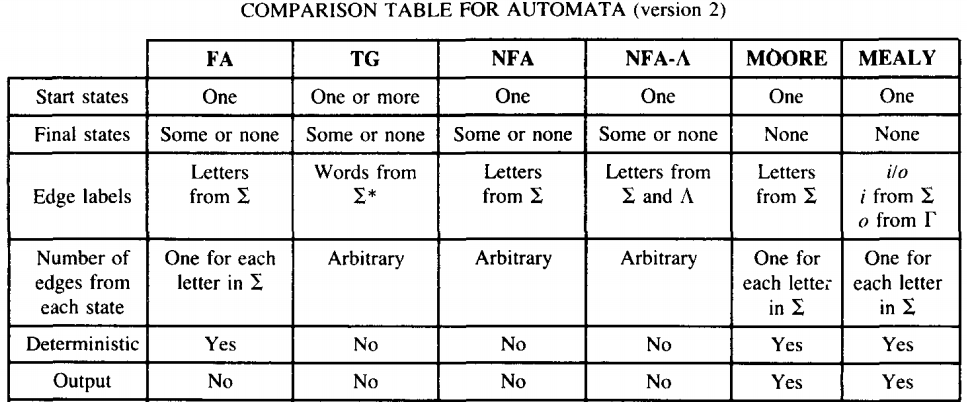
REGULAR LANGUAGES
A language that can be defined by a regular expression is called a regular language.
If L1 and L2 are regular languages, then L1 + L2 , L1L2 and L1* are also regular languages.
L1 + L2 means the language of all words in either L1 or L2. L1L2 means the language of all words formed by concatentating a word from L1 with a word from L2. L1* means strings that are the concatenation of arbitrarily many factors from L1. The result stated in this theorem is often expressed by saying: The set of regular languages is closed under union, concatenation, and the Kleene star operator.
PROOF 1 (by Regular Expressions) If L1 and L2 are regular languages, there are regular expressions r1 and r2 that define these languages.
Then (r1 + r2) is a regular expression that defines the language L1 + L2. The language L1L2 can be defined by the regular expression r1r2. The language L1* can be defined by the regular expression (rl)*.
Therefore, all three of these sets of words are definable by regular expressions and so are themselves regular languages.
Example of above proof
Let the alphabet be Σ = {a,b}.
Let L1 = all words of two or more letters that begin and end with the same letter and L2 = all words that contain the substring aba
For these languages we will use the following TG's and regular expressions:
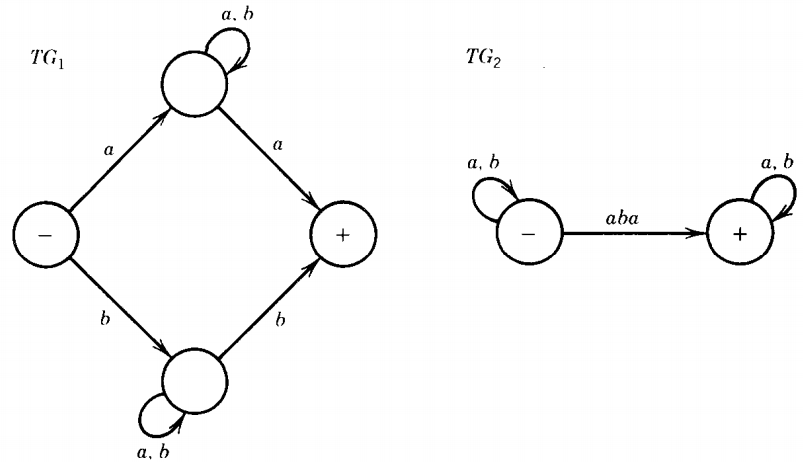
r1 = a(a + b)*a + b(a + b)*b ; r2 = (a + b)* aba (a + b)*
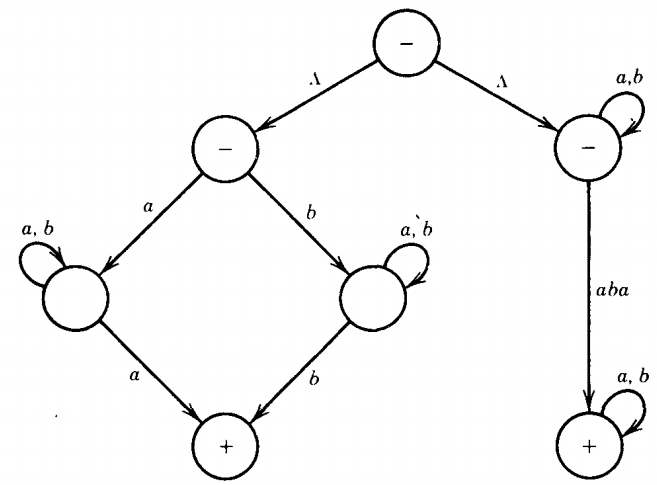
The language L1 + L2 is regular because it can be defined by the regular expression: [a(a+b)*a + b(a+b)*b] + [(a+b)* aba (a+b)*] (for the purpose of clarity we have employed brackets instead of nested parentheses) and is accepted by the TG:
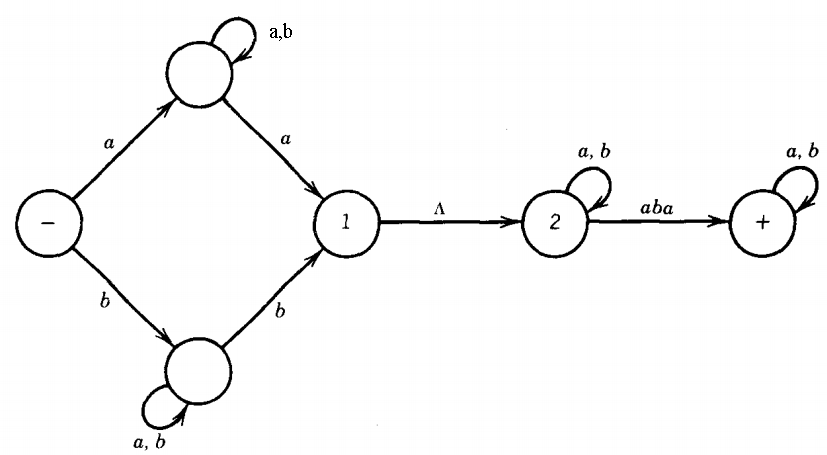
The language L1L2 is regular because it can be defined by the regular expression: [a(a+b)*a + b(a+b)*b] [(a+b)* aba (a+b)*] and is accepted by the TG:
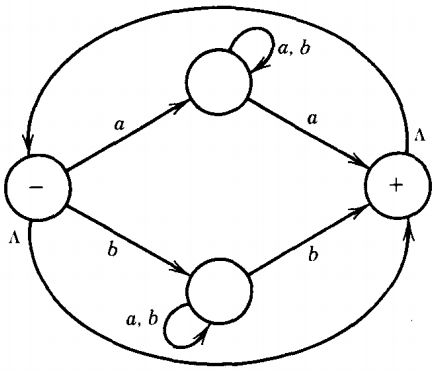
The language L1* is regular because it can be defined by the regular expression: [a(a+b)*a + b(a+b)*b]* and is accepted by the TG:
DEFINITION
If L is a language over the alphabet, Σ, we define its complement, L', to be the language of all strings of letters from Σ that are not words in L. Many authors use the bar notation \( \overline{L} \) to denote the complement of the language L, but, as with most writing for computers, we will use the more typable form.
EXAMPLE If L is the language over the alphabet = Σ = {a,b} of all words that have a double a in them, then L' is the language of all words that do not have a double a. It is important to specify the alphabet Σ or else the complement of L might contain "cat", "dog", "frog". . , since these are definitely not strings in L. Notice that the complement of the language L' is the language L. We could write this as L''= L. This is a theorem from Set Theory that is not restricted only to languages.
THEOREM 11 : If L is a regular language, then L' is also a regular language. In other words, the set of regular languages is closed under complementation
If L is a regular language, we know from Kleene's Theorem that there is some FA that accepts the language L.
Some of the states of this FA are final states and, most likely, some are not.
Let us reverse the final status of each state, that is, if it was a final state, make it a nonfinal state, and if it was a nonfinal state, make it a final state.
If an input string formerly ended in a nonfinal state, it now ends in a final state and vice versa.
This new machine we have built accepts all input strings that were not accepted by the original FA (all the words in L') and rejects all the input strings that the FA used to accept (the words in L).
Therefore, this machine accepts exactly the language L'. So by Kleene's Theorem, L' is regular.
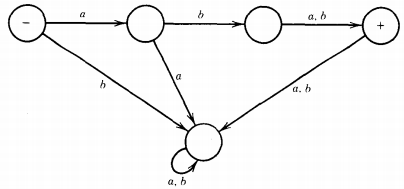
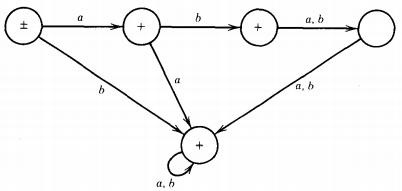
EXAMPLE : An FA that accepts only the strings aba and abb is shown below:
An FA that accepts all strings other than aba and abb is
Notice that we have to reverse the final/nonfinal status of the start state as well.
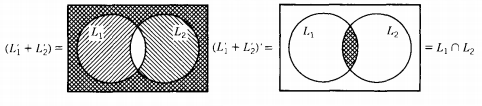
THEOREM 12 :If L1 and L2 are regular languages, then L1 ∩ L2 is also a regular language. In other words, the set of regular languages is closed under intersection.
By DeMorgan's Law for sets of any kind (regular languages or not): L1 ∩ L2 = (L1' + L2')'
This is illustrated by the Venn diagrams below.
This means that the language L1 ∩ L2 consists of all words that are not in either L1' or L2'. Since L1 and L2 are regular, then so are L1' and L2 '.
Since L1' and L2' are regular, so is L1' + L2 '.
And since L1' + L2' is regular, then so is (L1' + L2')', which means L1 ∩ L2 is regular.
EXAMPLE : Let us work out one example in complete detail. We begin with two languages over Σ = {a,b}.
L1 = all strings with a double a
L2 = all strings with an even number of a's.
These languages are not the same, since aaa is in L1 but not in L2 and aba is in L2 but not in L1 . They are both regular languages because they are defined by the following regular expressions (among others). r1 = (a + b)*aa(a + b)* ; r2 = b*(ab*ab*)*
The regular expression r2 is somewhat new to us. A word in the language L2 can have some b's in the front, but then whenever there is an a it is balanced (after some b's) by another a.
This gives us factors of the form (ab*ab*). The word can have as many factors of this form as it wants. It can end in an a or a b. Since these two languages are regular, Kleene's Theorem says that they can also be defined by FA's.
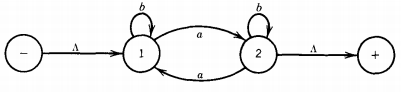
The two smallest of these are:
In the first machine we stay in the start state until we read our first a, then we move to the middle state. This is our opportunity to find a double a. If we read another a from the input string while in the middle state, we move to the final state where we remain. If we miss our chance and read a b, we go back to -. If we never get past the middle state, the word has no double a and is rejected.
The second machine switches from left state to right state or from right state to left state every time it reads an a. It ignores all b's. If the string begins on the left and ends on the left, it must have made an even number of left/right switches. Therefore, the strings this machine accepts are exactly those in L2.
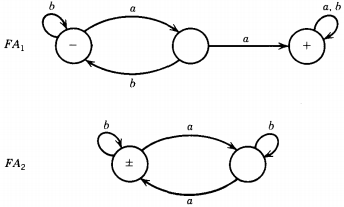
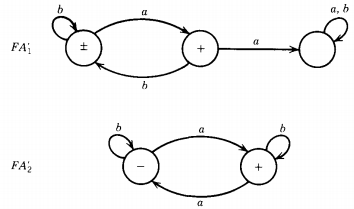
Now the first step in building the machine (and regular expression) for L1 &sap; L2 is to find the machines that accept the complementary languages L1' and L2'. Although it is not necessary for the successful execution of the algorithm, the English description of these languages is:
L1' = all strings that do not contain the substring aa
L2' = all strings having an odd number of a's
In the proof of the theorem that the complement of a regular language is regular we gave the algorithm for building the machines that accept these languages. All that we have to do is reverse what is a final state and what is not a final state. The machines for these languages are then :
Even if we are going to want both the regular expression and the FA for the intersection language, we do not need to find the regular expressions that go with these two component machines.
However, it is good exercise and the algorithm for doing this was presented as part of the proof of Kleene's Theorem.
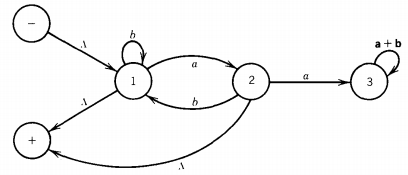
Recall that we go through stages of transition graphs with edges labeled by regular expressions. FA1' becomes:
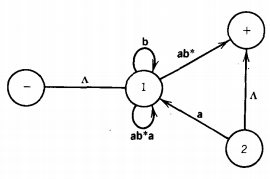
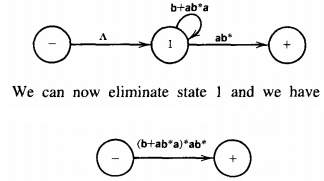
State 3 is part of no path from - to +, so it can be dropped. When we eliminate the edge from state 2 to state 1, we are destroying a loop of ab at state 1, a loop of bb*a at state 2, and the path: state 2, state 1, +, which adds a bb*-edge from 2 to +.
The possible paths from - to + are now from - to state 1 to +, which is labeled (b + ab)*, and from - to state 1 to state 2 to + labeled (b + ab)*a(bb*a)*(A + bb*)
The regular expression we have produced for L1 ' is then: (b + ab)* + (b + ab)*a(bb*a)*(A + b*)
There are many regular expressions for this set. Rather than use this complicated formula, let us note that the term (b + ab)* alone covers all words that have no double a and end in b.
Therefore, we can produce the same set by adding the factor (nothing or a) to the end of this expression: r1' = (b + ab)*(A + a)
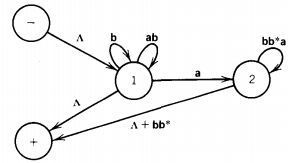
This is the regular expression we use for L1'. Let us now do the same thing for the language L2'. FA2' becomes:
Let us start the simplification of this picture by eliminating the edge from state 1 to state 2.
We must ask what paths this destroys that we must replace. One path it destroys is a loop back to state 1. We replace this with a loop at state 1 labeled ab*a, which is what the old loop through state 2 amounted to.
The other path this elimination destroys is the path from state 1 to state 2 to state +. We must include an edge for this path labeled ab*. This picture is now:
We can now see that there is no way to get to state 2, so it cannot be part of any path from - to +.
Therefore, we can eliminate it and its two edges. (Strictly speaking, to work entirely according to the algorithm, we should eliminate its edges first and then notice that it can be dropped.
We have taken the liberty of taking an insightful shortcut.) The two loops at state 1 can be combined to give:
which gives us the regular expression r2' = (b + ab*a)*ab* This is one of several regular expressions that define the language of all words with an odd number of a's.
Another is b*ab*(ab*ab*)* which we get by adding the factor b*a in front of the regular expression for L1.
This works because words with an odd number of a's can be interpreted as b*a in front of words with an even number of a's. The fact that these two different regular expressions define the same language is not obvious.
We now have regular expressions for L1' and L2 ', so we can write the regular expression for L1' + L2'. This will be r1' + r 2' = (b + ab)*(A + a) + (b + ab*a)*ab*
We must now go in the other direction and make this regular expression into an FA so that we can take its complement to get the FA that defines L1 ∩ L2.
To build the FA that corresponds to a complicated regular expression is no picnic, as we remember from the proof of Kleene's Theorem.
An alternative approach is to make the machine for L1' + L2' directly from the machines for L1' and L2' without resorting to regular expressions. We have already developed the method of building a machine that is the sum of two FA's also in the proof of Kleene's Theorem.
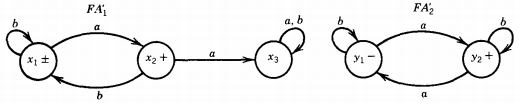
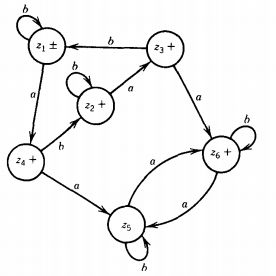
Let us label the states in the two machines for FA1' and FA2' as shown:
where the start states are x1 and y1 and the final states are x1 , x2, and Y2.
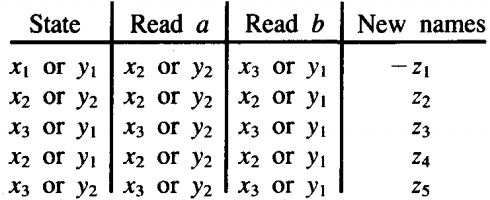
The six possible combination states are:
z1= x1 or y1 start, final (words ending here are accepted in FA1')
Z2 = x, or Y2 final (words ending here are accepted on FA1 ' and FA2')
Z3 = x2 or yj final (words ending here are accepted on FA1 ')
Z4 = x2 or Y2 final (words ending here are accepted on FA1' and FA2')
Z5 = x3 or y1 not final
Z6 = x3 or Y2 final (words ending here are accepted on FA2')
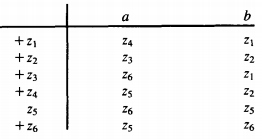
The transition table for this machine is:
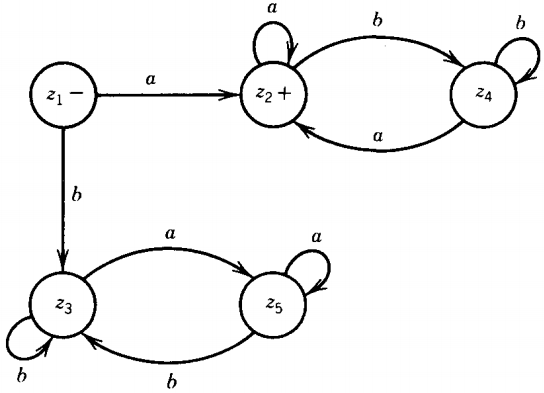
And so the machine can be pictured like this:
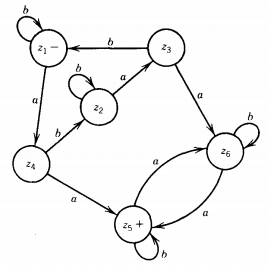
This is an FA that accepts the language L1' + L2'. If we reverse the status of each state from final to nonfinal and vice versa, we produce an FA for the language L1 ∩ L2. This is it:
This can be made into a regular expression as follows. First we observe there is only one - and one +, so we do not have to add extra terminal states.
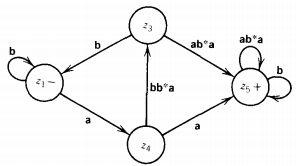
Let us begin by removing the edge from z2 to z3. The whole path from z4 to z2 to z3 can be replaced with an edge labeled bb*a.
Let us also eliminate the edge from z3 to z6 and let z3 go directly into + on an edge labeled ab*a.
There is no need to include in the z3 path the possible looping back and forth between z6 and + that can be done once z3 leads into +.
Once we get to +, we can hop out and back again. We can then replace z6 with a loop at + labeled ab*a.
The picture is now
There are now two paths that start at - and go back to -, the simple loop at - and the circuit - to z4 to z3 to -. The second path can be reduced to the loop labeled (abb*ab), and we can then remove the edge from z3 to -. From z4 to + there are two paths: one by way of z3 and the other direct.
We can remove the edge Z4 to Z3 (and then the whole state z3) by labeling the direct edge z4 to + with both alternatives as shown below
This whole machine reduces to the regular expression: (b + abb*ab)*a(a + bb*aab*a)(b + ab*a)*
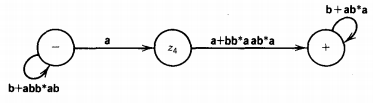
Analysis : (b + abb*ab)*a(a + bb*aab*a)(b + ab*a)*
As it stands, there are four factors (the second is just an a and the first and fourth are starred).
Every time we use one of the options from the two end factors we incorporate an even number of a's into the word (either none or two).
The second factor gives us an odd number of a's (exactly one). The third factor gives us the option of taking either one or three a's.
In total, the number of a's must be even. So all the words in this language are in L2.
The second factor gives us an a, and then we must immediately concatenate this with one of the choices from the third factor. If we choose the a, then we have formed a double a.
If we choose the other expression, bb*aab*a, then we have formed a double a in a different way. By either choice the words in this language all have a double a and are therefore in L1.
This means that all the words in the language of this regular expression are contained in the language L1 ∩ L2 . But are all the words in L1 ∩ L2 included in the language of this expression?
The answer to this is yes. Let us look at any word that is in L, n L 2. It has an even number of a's and a double a somewhere in it. There are two possibilities to consider separately:
Before the first double a there are an even number of a's.
Before the first double a there are an odd number of a's.
Words of type 1 come from the expression below. (even number of a's but not doubled) (first aa) (even number of a's may be doubled)
= (b + abb*ab)* (aa)(b + ab*a)* = type 1.
Notice that the third factor defines the language L1 and is a shorter expression than the r1 we used above. Words of type 2 come from the expression:
(odd number of not doubled a's) (first aa)
(odd number of a's may be doubled)
Notice that the first factor must end in b, since none of its a's is part of a double a.
= [(b + abb*ab)*abb*] aa [b*a(b + ab*a)*]
= (b + abb*ab)*(a)(bb* aab*a)(b + ab*a)*
= type 2
Adding type 1 and type 2 together (and factoring out like terms using the distributive law), we obtain the same expression we got from the algorithm. We now have two proofs that this is indeed a regular expression for the language L1 ∩ L2.
Example of intersection
Our two languages will be
L1= all words that begin with an a
L2= all words that end with an a
rl= a (a + b)*
r2 = (a + b)*a
The intersection language will be L1 ∩ L2 = all words that begin and end with the letter a
The language is obviously regular since it can be defined by the regular expression a(a + b)*a + a
Note that the first term requires that the first and last a's be different, which is why we need the second choice "+ a."
In this example we were lucky enough to "understand" the languages, so we could concoct a regular expression that we "understand" represents the intersection.
In general, this does not happen, so we follow the algorithm presented in the proof, which we can execute even without the benefit of understanding.
For this we must begin with FA's that define these languages:
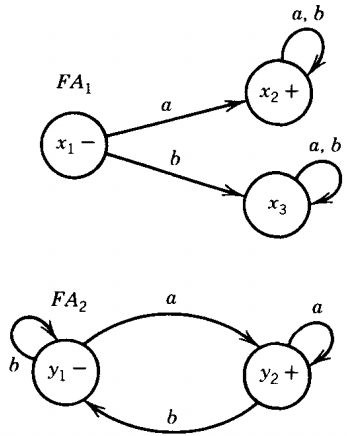
As it turns out, even though the two regular expressions are very similar, the machines are very different. There is a three-state version of FA2 but no two-state version of FA1.
We now build the transition table of the machine that runs its input strings on FA1 and FA2 simultaneously
The machine looks like this:
If were building the machine for L1 + L2 = all words in either L1 or L2 or in both
We would put + 's at any state representing acceptance by L1 or L2 , that is, any state with an x2 or a y2:
Z2 +
Z4 +
Z5 +
Since we are instead constructing the machine for L1 ∩ L2 = all words in both L1 and L2
we put a + only after the state that represents acceptance by both machines at once: Z2 + = X2 or Y2
Strings ending here are accepted by FA1 if being run on FA1 (by ending in x2 ) and by FA2 if being run on FA2 (by ending in Y2).
Do not be fooled by this slight confusion Z2 = X2 or Y2 = accepted by FA1 and by FA2
Caution : The poor plus sign is perilously overworked
2 + 2 (sometimes read "2 and 2 are 4")
(a + b)* (a or b repeated as often as we choose)
a+ (a string of at least one a)
L1 + L2 (all words in L1 or in L2)
+ z2, z2 + (z2 is a final state, the machine accepts input strings if they end here)