CONTEXT-FREE GRAMMARS - UPSC FEVER

The conversion from a high-level language into assembler language code is done by a program called the compiler. This is a superprogram.

Its data are other people's programs. It processes them and prints out an equivalent program written in assembler language. To do this it must figure out in what order to perform the complicated set of arithmetic operations that it finds written out in the one-line formula.

It must do this in a mechanical, algorithmic way. It cannot just look at the expression and understand it. Rules must be given by which this string can be processed.

Consider the language of valid input strings over the alphabet 0 1 2 3 4 5 6 7 8 9 + - / * ) (

Could some FA, directed from state to state by the input of a one-line formula, print out the equivalent assembly-language program? This would have to be an output FA like the Mealy or Moore machines for which the output alphabet would be assembler language statements.

We also want our machine to be able to reject strings of symbols that make no sense as arithmetic expressions, such as "((9)+". This input string should not take us to a final state in the machine. However, we cannot know that this is a bad input string until we have reached the last letter.

If the + were changed to a ), the formula would be valid. An FA that translated expressions into instructions as it scanned left to right would already be turning out code before it realized that the whole expression is nonsense.

Before we try to build a compiling machine, let us return to the discussion of what is and what is not a valid arithmetic expression All valid arithmetic expressions can be built up from the following rules.

Anything not produceable from these rules is not a valid arithmetic expression AE:

Rule 1 Any number is in the set AE.

Rule 2 If x and y are in AE then so are: (x) - (x) (x + y) (x - y) (x*y) (x/y) (x**y)

First we must design a machine that can figure out how a given input string was built up from these basic rules. Then we should be able to translate this sequence of rules into an assembler language program, since all of these rules are pure assembler language instructions

For example, if we present the input string ((3 + 4) * (6 + 7)) and the machine discovers that the way this can be produced from the rules is by the sequence

3 is in AE
4 is in AE
(3 + 4) is in AE
6 is in AE
7 is in AE
(6 + 7) is in AE
((3 + 4) * (6 + 7)) is in AE

we can automatically convert this into
LOAD 3 in Register 1
LOAD 4 in Register 2
ADD the contents of Register 2 into Register 1
LOAD 6 in Register 3
LOAD 7 in Register 4
ADD the contents of Register 3 into Register 4
MULTIPLY Register 1 by Register 4

or some such sequence of instructions depending on the architecture of the particular machine (not all computers have so many arithmetic registers) and the requirements of the particular assembler language (multiplication is not always available).

The hard part of the problem is to figure out by mechanical means how the input string can be produced from the rules. The second part-given the sequence of rules that create the expression to write a computer program to duplicate this process-is easy.

The designers of the first high-level languages realized that this problem is analogous to the problem humans have to face hundreds of times every day when they must decipher the sentences that they hear or read in English.

Elementary School used to be called Grammar School because one of the most important subjects taught was English Grammar.

A grammar is the set of rules by which the valid sentences in a language are constructed. Our ability to understand what a sentence means is based on our ability to understand how it could be formed from the rules of grammar.

Determining how a sentence can be formed from the rules of grammar is called parsing the sentence.

Rules that involve the meaning of words we call semantics and rules that do not involve the meaning of words we call syntax. In English the meaning of words can be relevant but in arithmetic the meaning of numbers is rarely cataclysmic. In the high-level computer languages, one number is as good as another. If

X=B+9
is a valid formulation then so are
X = B + 8 X = B + 473 X = B + 9999

So long as the constants do not become so large that they are out of range, and we do not try to divide by 0, and we do not try to take the square root of a negative number, and we do not mix fixed-point numbers with floatingpoint numbers in bad ways, one number is as good as another.

It could be argued that such rules as "thou shalt not divide by zero" as well as the other restrictions mentioned are actually semantic laws, but this is another interesting point that we shall not discuss.

In general, the rules of computer language grammar are all syntactic and not semantic.

There is another way in which the parsing of arithmetic expressions is easier than the parsing of English sentences. To parse the English sentence, "Birds sing." it is necessary to look up in a dictionary whether "birds" is a noun or a verb. To parse the arithmetic expression "(3 + 5)*6" it is not necessary to know any other characteristics of the numbers 3, 5, and 6.

The words that cannot be replaced by anything are called terminals. Words that must be replaced by other things we call nonterminals.

Here we have used the word "Start" to begin the process, as we used the word "Sentence" in the example of English. Aside from Start, the only other nonterminal is AE. The terminals are the phrase "any number" and the symbols + - * /** ( )

Either we could be satisfied that we know what is meant by the words "any number" or else we could define this phrase by a set of rules, thus converting it from a terminal into a nonterminal.

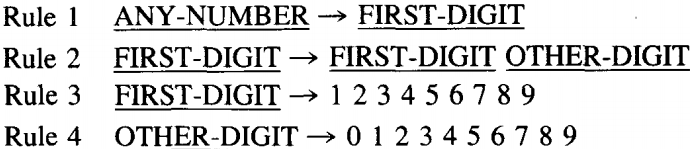
Rules 3 and 4 offer choices of terminals. We put spaces between them to indicate "choose one," but we soon shall introduce another disjunctive symbol.

We can produce the number 1066 as follows:

Here we have made all our substitutions of terminals for nonterminals in one swoop, but without any possible confusion. One thing we should note about the definition of AE is that some of the grammatical rules involve both terminals and nonterminals together.

In English, the rules were either of the form
one Nonterminal - string of Nonterminals
or
one Nonterminal - choice of terminals

In our present study, we shall see that the form of the grammar has great significance.

The sequence of applications of the rules that produces the finished string of terminals from the starting symbol is called a derivation. The grammatical rules are often called productions.

They all indicate possible substitutions. The derivation may or may not be unique, by which we mean that by applying productions to the start symbol in two different ways we may still produce the same finished product.

We call this new structure a context-free grammar or CFG

A context-free grammar, called a CFG, is a collection of three things:

An alphabet Σ of letters called terminals from which we are going to make strings that will be the words of a language.

A set of symbols called nonterminals, one of which is the symbol S, standing for "start here."

A finite set of productions of the form
one nonterminal -> finite string of terminals and/or nonterminals

We require that at least one production has the nonterminal S as its left side.

So as not to confuse terminals and nonterminals, we always insist that nonterminals be designated by capital letters while terminals are usually designated by lowercase letters and special symbols.

The language generated by a CFG is the set of all strings of terminals that can be produced from the start symbol S using the productions as substitutions.

A language generated by a CFG is called a context-free language, abbreviated CFL

There is no great uniformity of opinion among experts about the terminology to be used here.

The language generated by a CFG is sometimes called the language defined by the CFG, or the language derived from the CFG, or the language produced by the CFG.

This is similar to the problem with regular expressions.

We should say "the language defined by the regular expression" although the phrase "the language of the regular expression" has a clear meaning.

We usually call the sequence of productions that form a word a derivation or a generation of the word.

Example :
Let the only terminal be a.
Let the productions be:
PROD 1 S -> aS
PROD 2 S -> Λ

If we apply Production 1 six times and then apply Production 2, we generate the following:

S → aS
→ aaS
→ aaaS
→ aaaaS
→ aaaaaS
→ aaaaaaS
→ aaaaaaΛ
→ aaaaaa

This is a derivation of a⁶ in this CFG. The string aⁿ comes from n applications of Production 1 followed by one application of Production 2.

If we apply Production 2 without Production 1, we find that the null string is itself in the language of this CFG.

Since the only terminal is a it is clear that no words outside of a* can possibly be generated. The language generated by this CFG is exactly a*.

In the examples above, we used two different arrow symbols. The symbol "--->" we employ in the statement of the productions.

It means "can be replaced by", as in S -> aS.

The other arrow symbol "⇒" we employ between the unfinished stages in the generation of our word. It means "can develop into" as in aaS ⇒ aaaS. These "unfinished stages" are strings of terminals and nonterminals that we shall call working strings.

Notice that in this last example we have both S → aS as a production in the abstract and S ⇒ aS as the first step in a particular derivation.

EXAMPLE

Let the only terminal be a.
Let the productions be:
PROD 1 S → SS
PROD 2 S → *a
PROD 3 S → A

In this language we can have the following derivation.
S ⇒ SS
⇒ SSS
⇒ SaS
⇒ SaSS
⇒ ΛaSS
⇒ ΛaaS
⇒ ΛaaΛ
= aa

The language generated by this set of productions is also just the language a*, but in this case the string aa can be obtained in many (actually infinitely many) ways.

In the first example there was a unique way to produce every word in the language.

This also illustrates that the same language can have more than one CFG generating it.

Notice above that there are two ways to go from SS to SSS - either of the two S's can be doubled.

In the previous example the only terminal is a and the only nonterminal is S. What then is Λ? It is not a nonterminal since there is no production of the form Λ --> something

Yet it is not a terminal since it vanishes from the finished string ΛaaΛ = aa. As always, Λ is a very special symbol and has its own status.

In the definition of a CFG we said a nonterminal could be replaced by any string of terminals and/or nonterminals even the empty string.

To replace a nonterminal by A is to delete it without leaving any tangible remains.

For the nonterminal N the production N ----> Λ means that whenever we want, N can simply be deleted from any place in a working string.

Example

Let the only terminal be a.
Let the productions be:
PROD 1 : S → SS
PROD 2 : S → a
PROD 3 : S → Λ

In this language we can have the following derivation.

S ⇒ SS
⇒ SSS
⇒ SaS
⇒ SaSS
⇒ ΛaSS
⇒ ΛaaS
⇒ ΛaaΛ
= aa

The language generated by this set of productions is also just the language a*, but in this case the string aa can be obtained in many (actually infinitely many) ways.

In the first example there was a unique way to produce every word in the language.

This also illustrates that the same language can have more than one CFG generating it.

Notice above that there are two ways to go from SS to SSS -either of the two S's can be doubled.

In the previous example the only terminal is a and the only nonterminal is S. What then is Λ? It is not a nonterminal since there is no production of the form Λ --> something

Yet it is not a terminal since it vanishes from the finished string ΛaaΛ = aa. As always, Λ is a very special symbol and has its own status.

In the definition of a CFG we said a nonterminal could be replaced by any string of terminals and/or nonterminals even the empty string.

To replace a nonterminal by Λ is to delete it without leaving any tangible remains. For the nonterminal N the production N -> Λ means that whenever we want, N can simply be deleted from any place in a working string.

Let the terminals be a and b, let the only nonterminal be S, and let the productions be

PROD 1 : S → aS
PROD 2 : S → bS
PROD 3 : S → a
PROD 4 : S → b

We can produce the word baab as follows:

S ⇒ bS (by PROD 2)
⇒ baS (by PROD 1)
⇒ baaS (by PROD 1)
⇒ baab (by PROD 4)

The language generated by this CFG is the set of all possible strings of the letters a and b except for the null string, which we cannot generate.

We can generate any word by the following algorithm:

At the beginning the working string is the start symbol S. Select a word to be generated.

Read the letters of the desired word from left to right one at a time.

If an 'a' is read that is not the last letter of the word, apply PROD 1 to the working string.

If a 'b' is read that is not the last letter of the word, apply PROD 2 to the working string.

If the last letter is read and it is an 'a', apply PROD 3 to the working string.

If the last letter is read and it is a 'b', apply PROD 4 to the working string.

At every stage in the derivation before the last, the working string has the form (string of terminals) S

At every stage in the derivation, to apply a production means to replace the final nonterminal S. Productions 3 and 4 can be used only once and only one of them can be used. For example, to generate babb we apply in order Prods 2, 1, 2, 4, as below:

S ⇒ bS ⇒ baS ⇒ babS ⇒ babb

Let the terminals be a and b. Let the nonterminals be S, X, and Y. Let the productions be:

S → X
S → y
X → Λ
Y → aY
Y → bY
Y → a
Y → b

All the words in this language are either of type X, if the first production in their derivation is S → X

or of type Y, if the first production in their derivation is S → Y

The only possible continuation for words of type X is the production X → Λ

Therefore Λ is the only word of type X.

The productions whose left side is Y form a collection identical to the productions in the previous example except that the start symbol S has been replaced by the symbol Y.

We can carry on from Y the same way we carried on from S before. This does not change the language generated, which contains only strings of terminals.

Therefore, the words of type Y are exactly the same as the words in the previous example. That means, any string of a's and b's except the null string can be produced from Y as these strings were produced before from S.

Putting the type X and the type Y words together, we see that the total language generated by this CFG is all strings of a's and b's, null or otherwise. The language generated is (a + b)*.

Let the terminals be a and b. Let the only nonterminal be S.

Let the productions be
S → aS
S → bS
S → a
S → b
S → Λ

The word ab can be generated by the derivation
S ⇒ aS
⇒ abS
⇒ abΛ
= ab

or by the derivation
S ⇒ aS
⇒ ab

The language of this CFG is also (a + b)*, but the sequence of productions that is used to generate a specific word is not unique.

If we deleted the third and fourth productions, the language generated would be the same.

Let the terminals be a and b, let the nonterminals be S and X, and let the productions be

S → XaaX
X → aX
X → bX
X → Λ

We already know from the previous example that the last three productions will allow us to generate any word we want from the nonterminal X.

If the nonterminal X appears in any working string we can apply productions to turn it into any word we want. Therefore, the words generated from S have the form : anything aa anything
or
(a + b)*aa(a + b)*

which is the language of all words with a double a in them somewhere. For example, to generate baabaab we can proceed as follows:

S ⇒ XaaX ⇒ bXaaX ⇒ baXaaX ⇒ baaXaaX ⇒ baabXaaX ⇒ baabΛaaX ⇒ baabaaX ⇒ baabaabX ⇒ baabaabΛ ⇒ baabaab

There are other sequences that also derive the word baabaab.

Let the terminals be a and b, let the nonterminals be S, X, and Y and let the productions be

S → XY X → aX X → bX X → a Y → Ya Y → Yb Y → a

What can be derived from X? Let us look at the X productions alone.

X → aX X → bX X → a

Beginning with the nonterminal X and starting a derivation using the first two productions we always keep a nonterminal X on the right end.

To get rid of the X for good we must eventually replace it with an a by the third production.

We can see that any string of terminals that comes from X must end in an a and any words ending in an a can be derived from X.

For example, to derive the word babba from X we can proceed as follows:

X ⇒ bX ⇒ baX ⇒ babX ⇒ babbX ⇒ babba

Similarly, the words that can be derived from Y are exactly those that begin with an a. To derive abbab, for example, we can proceed:

Y ⇒ Yb ⇒ Yab ⇒ Ybab ⇒ Ybbab ⇒ abbab

A Y always stays on the left end until it is replaced by an a. When an X part is concatenated with a Y part, a double a is formed.

We can conclude that starting from S we can derive only words with a double a in them, and all of these words can be derived.

For example, to derive babaabb we know that the X part must end at the first a of the double a and that the Y part must begin with the second a.

S ⇒ XY ⇒ bXY ⇒ baXY ⇒ babXY ⇒ babaY
⇒ babaYb ⇒ babaYbb ⇒ babaabb

Let the terminals be a and b. Let the three nonterminals be S, BALANCED, and UNBALANCED. We treat these nonterminals as if they were each a single symbol and nothing more confusing. Let the productions be

S → SS
S → BALANCED S
S → S BALANCED
S → Λ
S → UNBALANCED S UNBALANCED
BALANCED → aa
BALANCED → bb
UNBALANCED → ab
UNBALANCED → ba

We shall show that the language generated from these productions is the set of all words with an even number of a's and an even number of b's. This is our old friend, the language EVEN-EVEN.

To prove this we must show two things: that all the words in EVEN-EVEN can be generated from these productions and that every word generated from these productions is in fact in the language EVEN-EVEN.

First we show that every word in EVEN-EVEN can be generated by these productions.

From our earlier discussion of the language EVEN-EVEN we know that every word in this language can be written as a collection of substrings of type aa or type bb or type (ab + ba) (aa + bb)* (ab + ba).

All three types can be generated from the nonterminal S from productions above. The various substrings can be put together by repeated application of the production : S → SS

This production is very useful. If we apply it four times we can turn one S into five S's. Each of these S's can be a syllable of any of the three types. For example, the EVEN-EVEN word aababbab can be produced as follows:

S ⇒ BALANCED S
⇒ aaS
⇒ aa UNBALANCED S UNBALANCED
⇒ aa ba S UNBALANCED Saa
⇒ aa ba S ab
⇒ aa ba BALANCED S ab
⇒ aa ba bb S ab
⇒ aa ba bb Λ ab
= aababbab

To see that all the words that are generated by these productions are in the language EVEN-EVEN we need only to observe that words derived from S can be decomposed into two-letter syllables and the unbalanced syllables, ab and ba, come into the working string in pairs, which add two a's and two b's.

Also, the balanced syllables add two of one letter and zero of the other letter.

The sum total of a's and b's will be the sum of even numbers of a's and even numbers of b's. Both the a's and the b's in total will be even. Therefore, the language generated by this CFG is exactly EVEN-EVEN