In old-fashioned English grammar courses students were often asked to diagram a sentence.

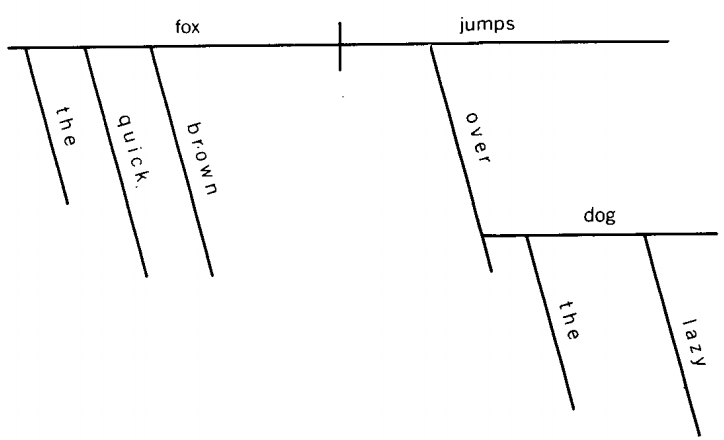
This meant that they were to draw a parse tree, which is a picture with the base line divided into subject and predicate.

All words or phrases modifying these were drawn as appendages on connecting lines. For example,

The quick brown fox jumps over the lazy dog becomes:

If the fox is dappled grey, then the parse tree would be

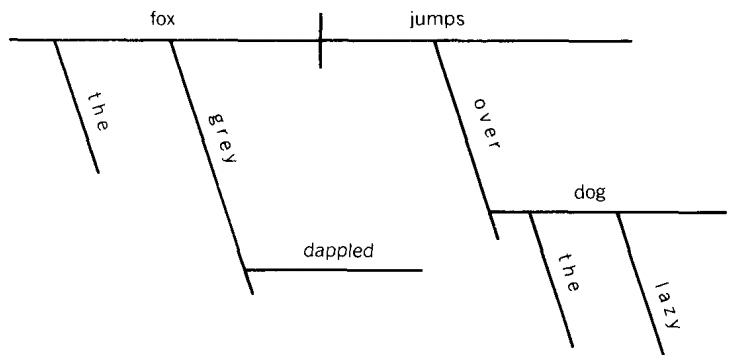
since dappled modifies grey and therefore is drawn as a branch off the grey line.

The sentence, "I shot the man with the gun." can be diagrammed in two ways:

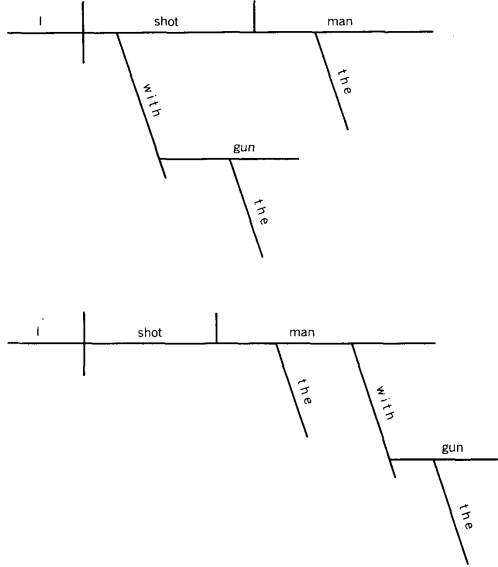
In the first diagram "with the gun" explains how I shot. In the second diagram "with the gun" explains who I shot.

These diagrams help us straighten out ambiguity. They turn a string of words into an interpretable idea by identifying who does what to whom.

A famous case of ambiguity is the sentence, "Time flies like an arrow."

We humans have no difficulty identifying this as a poetic statement, technically a simile, meaning, "Time passes all too quickly, just as a speeding arrow darts across the endless skies" or some such euphimism.

This is diagrammed by the following parse tree:

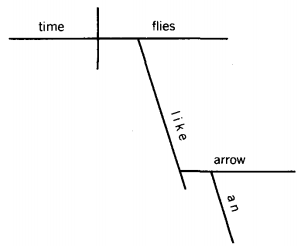
Notice how the picture grows like a tree when "an" branches from "arrow." A Graph Theory tree, unlike an arboreal tree, can grow sideways or upside down.

A non native speaker of English with no poetry in her soul (a computer, for example) who has just yesterday read the sentence, "Time flies like a banana." might think the sentence should be diagrammed as

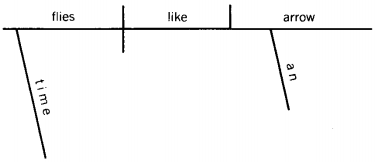
where she thinks "time flies" may have even shorter lives than drosophilae.

Looking in our dictionary, we see that "time" is also a verb, and if so in this case, the sentence could be in the imperative mood with the understood subject "you," in the same way that "you" is the understood subject of the sentence "Close the door."

A race track tout may ask a jockey to do a favor and "Time horses like a trainer" for him. The computer might think this sentence should be diagrammed:

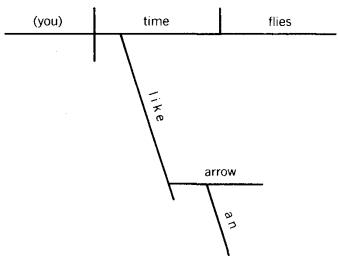
Someone is being asked to take a stopwatch and "time" some racing "flies" just as "an arrow" might do the same job, although one is unlikely to meet a straight arrow at the race track.

The idea of diagramming a sentence to show how it should be parsed carries over easily to CFG's. We start with the symbol S.

Every time we use a production to replace a nonterminal by a string, we draw downward lines from the nonterminal to each character in the string.

Let us illustrate this on the CFG

S → AA
A → AAA | bA | Ab | a
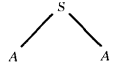
We begin with S and apply the production S → AA

To the left-hand A let us apply the production A → bA. To the right-hand A let us apply A → AAA.

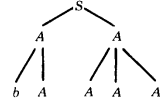
The b that we have on the bottom line is a terminal, so it does not descend further. In the terminology of trees it is called a terminal node. Let the four A's, left to right, undergo the productions A → bA, A → a, A → a, A → Ab respectively. We now have

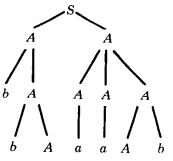
Let us finish off the generation of a word with the productions A → a and A → a:

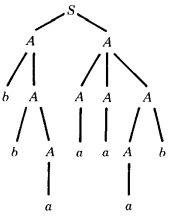
Reading from left to right, the word we have produced is bbaaaab. As was the case with diagramming a sentence, we understand more about the finished word if we see the whole tree.

The third and fourth letters are both a's, but they are produced by completely different branches of the tree. These tree diagrams are called syntax trees or parse trees or generation trees or production trees or derivation trees.

The variety of names comes from the multiplicity of applications to linguistics, compiler design, and mathematical logic.

The only rule for formation of such a tree is that every nonterminal sprouts branches leading to every character in the right side of the production that replaces it.

If the nonterminal N can be replaced by the string abcde: N → abcde then in the tree we draw:

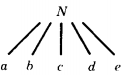
There is no need to put arrow heads on the edges because the direction of production is always downward

One CFG for a subsystem of Propositional Calculus is: S → (S) | S ⊃ S | ~S | p | q

The only nonterminal is S. The terminals are p q ~ ⊃ ( ) where "⊃" is the symbol for implication.

In this grammar consider the diagram:

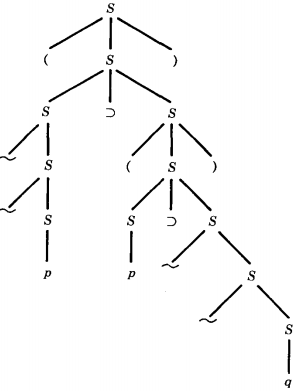
This is a derivation tree for the 13-letter word (~~ p ⊃ (p ⊃ ~~ q))

We often say that to know the derivation tree for a given word in a given grammar is to understand the meaning of that word.

The concept of "meaning" is one that we shall not deal with mathematically in this book. We never presumed that the languages generated by our CFG's have any significance beyond being formal strings of symbols.

However, in some languages the meaning of a string of symbols is important to us for reasons of computation.

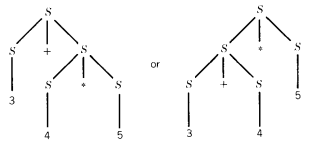
Let us concentrate for a moment on an example of a CFG for a simplified version of arithmetic expressions: S → S + S | S * S | number

Let us presume that we know precisely what is meant by "number." We are all familiar with the ambiguity inherent in the expression 3 + 4 * 5

Does it mean (3 + 4) * 5, which is 35, or does it mean 3 + (4 * 5), which is 23?

In the language defined by this particular CFG we do not have the option of putting in parentheses for clarification. Parentheses are not generated by any of the productions and are therefore not letters in the derived language.

There is no question that 3 + 4 * 5 is a word in the language of this CFG. The only queston is what does this word mean in terms of calculation? It is true that if we insisted on parentheses by using the grammar:

S → (S + S) | (S * S) | number

we could not produce the string 3 + 4 * 5 at all. We could only produce

S → (S + S) → (S + (S*S))→ . . . →(3 + (4*5))
or
S → (S*S) → ((S + S)*S) → ... → ((3 + 4)* 5)

neither of which is an ambiguous expression. In the practical world we do not need to use all these cluttering parentheses because we have adopted the convention of "hierarchy of operators," which says that * is to be executed before +.

This, unfortunately, is not reflected in either grammar. Later, we present a grammar that generates unambiguous arithmetic expressions that will mean exactly what we want them to mean without the need for burdensome parentheses.

For now, we can only distinguish between these two possible meanings for the expression 3 + 4 * 5 by looking at the two possible derivation trees that might have produced it.

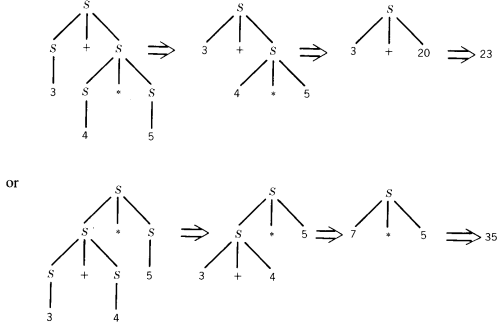We can evaluate an expression in parse-tree form from the tree picture itself by starting at the bottom and working our way up to the top, replacing each nonterminal as we come to it by the result of the calculation that it produces.

This can be done as follows :

These examples show how the derivation tree can explain what the word means in much the same way that the parse trees in English grammar explain the meaning of sentences.

In the special case of this particular grammar (not for CFG's in general), we can draw meaningful trees of terminals alone using the start symbol S only once.

This will enable us to introduce a new notation for arithmetic expressions--one that has direct applications to Computer Science

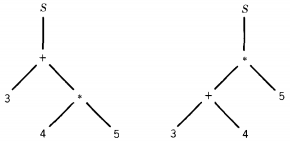
The method for drawing the new trees is based on the fact that + and * are binary operations that combine expressions already in the proper form.

The expression 3 + (4 * 5) is a sum. A sum of what? A sum of a number and a product. What product? The product of two numbers.

Similarly (3 + 4) * 5 is a product of a sum and a number, where the sum is a sum of numbers.

Notice the similarity to the original recursive definition of arithmetic expressions. These two situations are depicted in the following trees.

These are like derivation trees for the CFG: S → S + S | S * S | number except that we have eliminated most of the S's.

We have connected the branches directly to the operators instead.

The symbols * and + are no longer terminals, since they must be replaced by numbers. These are actually standard derivation trees taken from a new CFG in which S, * and + are nonterminals and number is the only terminal.

The productions are:
S → * | + | number
+ → + + | + * | + number | * + | ** | * number | number + |
number * | number number
* → + + | + * | + number | * + | * * | * number | number + |
number * | number number

As usual number has been underlined because it is only one symbol. The only words in this language are strings of number. But we are interested in the derivation trees themselves, not in these dull words.

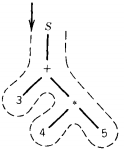
From these trees we can construct a new notation for arithmetic expressions. To do this, we walk around the tree and write down the symbols, once each, as we encounter them.

We begin our trip on the left side of the start symbol S heading south. As we walk around the tree, we keep our left hand always on the tree.

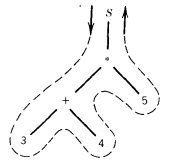
The first symbol we encounter on the first tree is +. This we write down as the first symbol of the expression in the new notation. Continuing to walk around the tree, keeping it on our left, we first meet 3 then + again.

We write down the 3, but this time we do not write + down because we have already included it in the string we are producing.

Walking some more we meet *, which we write down. Then we meet 4, then * again, then 5. So we write down 4, then 5.

There are no symbols we have not met, so our trip is done. The string we have produced is:

+ 3 * 4 5. The second derivation tree when converted into the new notation becomes: * + 3 4 5.

unless parentheses are required. We shall show that these strings are unambiguous in that each determines a unique calculation without the need for establishing the convention of times before plus.

These representations are said to be in operator prefix notation because the operator is written in front of the operands it combines.