Parse Tree - Tracing
Since S → S + S has changed from
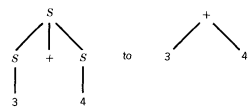
the left-hand tracing changes 3 + 4 into + 3 4.
To evaluate a string of characters in this new notation, we proceed as follows. We read the string from left to right. When we find the first substring of the form
operator-operand-operand (call this o-o-o for short)
we replace these three symbols with the one result of the indicated arithmetic calculation. We then rescan the string from the left.
We continue this process until there is only one number left, which is the value of the entire original expression.
In the case of the expression + 3 * 4 5, the first substring we encounter of the form operator - operand - operand is * 4 5, so we replace this with the result of the indicated multiplication, that is, the number 20.
The string is now + 3 20. This itself is in the form o-o-o, and we evaluate it by performing the addition.
When we replace this with the number 23 we see that the process of evaluation is complete.
In the case of the expression * + 3 4 5 we find that the o-o-o substring is + 3 4. This we replace with the number 7.
The string is then * 7 5, which itself is in the o-o-o form. When we replace this with 35, the evaluation process is complete.
Let us see how this process works on a harder example. Let us start with the arithmetic expression : ((1 + 2) * (3 + 4) + 5) * 6.
This is shown in normal notation, which is called operator infix notation because the operators are placed in between the operands.
With infix notation we often need to use parentheses to avoid ambiguity, as is the case with the expression above. To convert this to operator prefix notation, we begin by drawing its derivation tree:
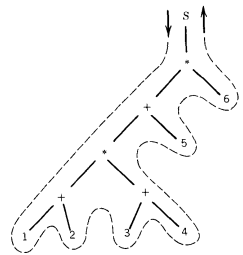
Reading around this tree gives the equivalant prefix notation expression * + * + 1 2 + 3 4 5 6
Notice that the operands are in the same order in prefix notation as they were in infix notation, only the operators are scrambled and all parentheses are deleted.
To evaluate this string we see that the first substring of the form operator operand - operand is + 1 2, which we replaced with the number 3.
The evaluation continues as follows:

which is the correct value for the expression we started with. Since the derivation tree is unambiguous, the prefix notation is also unambiguous and does not rely on the tacit understanding of operator hierarchy or on the use of parentheses.
EXAMPLE - Trees
Let us consider the language generated by the following CFG: PROD 1 S → AB
PROD 2 A → a
PROD 3 B → b
There are two different sequences of applications of the productions that generate the word ab. One is PROD 1, PROD 2, PROD 3. The other is PROD 1, PROD 3, PROD 2.
S ⇒ AB ⇒ aB ⇒ ab or S ⇒ AB ⇒ Ab ⇒ ab
However, when we draw the corresponding syntax trees we see that the two derivations are essentially the same:
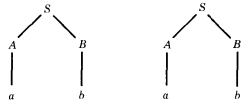
This example, then, presents no substantive difficulty because there is no ambiguity of interpretation.
This is related to the situation in which we first built up the grammatical structure of an English sentence out of noun, verb, and so on, and then substituted in the specific words of each category either one at a time or all at once.
When all the possible derivation trees are the same for a given word then the word is unambiguous.
DEFINITION
A CFG is called ambiguous if for at least one word in the language that it generates there are two possible derivations of the word that correspond to different syntax trees.
Let us reconsider the language PALINDROME, which we can now define by the CFG below:
S → aSa | bSb | a | b | λ
At every stage in the generation of a word by this grammar the working string contains only the one nonterminal S smack dab in the middle. The word grows like a tree from the center out. For example.:
... baSab ⇒ babSbab ⇒ babbSbbab ⇒ babbaSabbab ...
When we finally replace S by a center letter (or A if the word has no center letter) we have completed the production of a palindrome. The word aabaa has only one possible generation:
S ⇒ aSa
⇒ aaSaa
⇒ aabaa
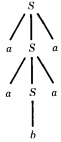
If any other production were applied at any stage in the derivation, a different word would be produced. We see then that this CFG is unambiguous.
EXAMPLE
The language of all nonnull strings of a's can be defined by a CFG as follows:
S → aS | Sa | a
In this case the word a3 can be generated by four different trees:
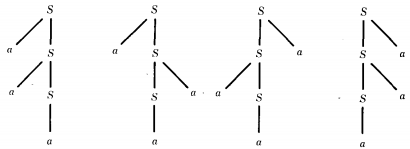
This CFG is therefore ambiguous.
However the same language can also be defined by the CFG:
S → aS | a
for which the word a3 has only one production:
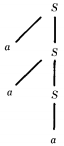
This CFG is not ambiguous.
DEFINITION
For a given CFG we define a tree with the start symbol S as its root and whose nodes are working strings of terminals and nonterminals.
The descendants of each node are all the possible results of applying every production to the working string, one at a time.
A string of all terminals is a terminal node in the tree. The resultant tree is called the total language tree of the CFG.
For the CFG
S → aa | bX | aXX
X → ab | b
the total language tree is:
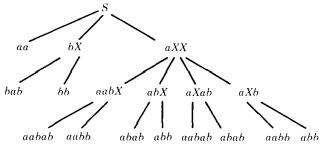
This total language has only seven different words. Four of its words (abb, aabb, abab, aabab) have two different possible derivations because they appear as terminal nodes in this total language tree in two different places.
However, the words are not generated by two different derivation trees and the grammar is unambiguous. For example:
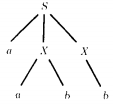
DEFINITION
Consider the CFG:
S → aSb | bS | a
We have the terminal letters a and b and three possible choices of substitutions for S at any stage. The total tree of this language begins:
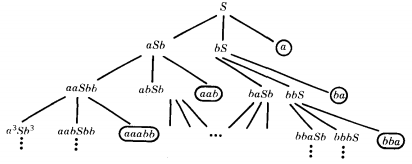
Here we have circled the terminal nodes because they are the words in the language generated by this CFG.
We say "begins" because since the language is infinite the total language tree is too.
We have already generated all the words in this language with one, two, or three letters.
L = {a ba aab bba ...}
These trees may get arbitrarily wide as well as infinitely long.
EXAMPLE
S → SAS | b
A → ba | b
Every string with some S's and some A's has many possible productions that apply to it, two for each S and two for each A.
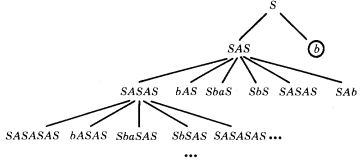
The essence of recursive definition comes into play in an obvious way when some nonterminal has a production with a right-side string containing its own name, as in this case:
X → (blah) X (blah)
The total tree for such a language then must be infinite since it contains the branch:
X ⇒ (blah) X (blah)
⇒ (blah) (blah) X (blah) (blah)
⇒ (blah)3 X (blah)3This has a deep significance which will be important to us shortly. Surprisingly, even when the whole language tree is infinite, the language may have only finitely many words.
EXAMPLE
Consider this CFG:
S →- X | b
X → aXThe total language tree begins:
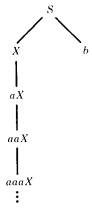
Clearly the only word in this language is the single letter b. X is a bad mistake; it leads to no words. It is a useless symbol in this CFG.
REGULAR GRAMMARS
Some of the examples of languages we have generated by CFG's have been regular languages, that is, they are definable by regular expressions. However, some nonregular languages that can also be generated by CFG's
EXAMPLE
The CFG:
S → ab | aSb
generates the language
{anbn}
Repeated applications of the second production results in the derivation
S ⇒ aSb ⇒ aaSbb ⇒ aaaSbbb ⇒ aaaaSbbbb ...
Finally the first production will be applied to form a word having the same number of a's and b's, with all the a's first.
EXAMPLE
The CFG:
S → aSa | bSa | Λ
generates the language TRAILING-COUNT of all words of the form:
s alength(s) for all strings s in (a + b)*
that is, any string concatenated with a string of as many a's as the string has letters. This language is also nonregularThe relationship between regular languages and context-free grammars
All languages can be generated by CFG's.
All regular languages can be generated by CFG's, and so can some nonregular languages but not all possible languages.
Some regular languages can be generated by CFG's and some regular languages cannot be generated by CFG's. Some nonregular languages can be generated by CFG's and some nonregular languages cannot.
Further, we shall indeed show that all regular languages can be generated by CFG's.
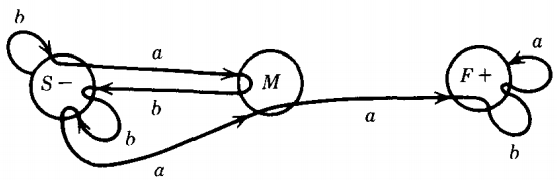
EXAMPLE - A method for turning an FA into a CFG
Let us consider the FA below, which accepts the language of all words with a double a:
We have named the start state S, the middle state M, and the final state F. The word abbaab is accepted by this machine.
Rather than trace through the machine watching how its input letters are read, as usual, let us see how its path grows.
The path has the following step-by-step development where a path is denoted by the labels of its edges concatenated with the symbol for the state in which it now sits :
S (We begin in S)
aM (We take an a-edge to M)
abS (We take an a-edge then a b-edge and we are in S)
abbS (An a-edge, a b-edge, and a b-loop back to S)
abbaM (Another a-edge and we are in M)
abbaaF (Another a-edge and we are in F)
abbaabF (A b-loop back to F)
abbaab (The finished path: an a-edge a b-edge . . . )
This path development looks very much like a derivation of a word in a CFG. What would the rules of production be ?
(From S an a-edge takes us to M) S → aM
(From S a b-edge takes us to S) S → bS
(From M an a-edge takes us to F) M → aF
(From M a b-edge takes us to S) M → bS
(From F an a-edge takes us to F) F → aF
(From F a b-edge takes us to F) F → bF
(When at the final state F, we can F → Λ
stop if we want to).We shall prove in a moment that the CFG we have just described generates all paths from S to F and therefore generates all words accepted by the FA.
Let us consider another path from S to F, that of the word babbaaba. The path development sequence is
(Start here) S
(A b-loop back to S) bS
(An a-edge to M) baM
(A b-edge back to S) babS
(A b-loop back to S) babbS
(An a-edge to M) babbaM
(Another a-edge to F) babbaaF
(A b-loop back to F) babbaabF
(An a-loop back to F) babbaabaF
(Finish up in F) babbaaba
This is not only a path development but also a derivation of the word babbaaba from the CFG above.
The logic of this argument is roughly as follows. Every word accepted by this FA corresponds to a path from S to F. Every path has a step-by-step development sequence as above. Every development sequence is a derivation in the CFG proposed. Therefore, every word accepted by the FA can be generated by the CFG.
The converse must also be true. We must show that any word generated by this CFG is a word accepted by the FA. Let us take some derivation such as
Production Used Derivation S → aM S ⇒ aM M → bS ⇒ abS S → aM ⇒ abaM M → aF ⇒ abaaF F → bF ⇒ abaabF F → Λ ⇒ abaab This can be interpreted as a path development:
Production Used Path Developed S → aM Starting at S we take an a-edge to M M → bS Then a b-edge to S S → aM Then an a-edge to M M → aF Then an a-edge to F F → bF Then a b-edge to F F → Λ Now we stop 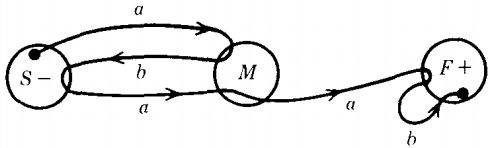
The path, of course, corresponds to the word abaab, which must be in the language accepted by the FA since its corresponding path ends at a final state.
The general rules for the algorithm above are:
CFG derivation → path development → path → word accepted
and
word accepted → path → path development → CFG derivationFor this correspondence to work, all that is necessary is that:
1. Every edge between states be a production:

and 2. Every production correspond to an edge between states:
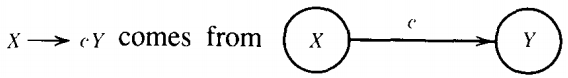
or to the possible termination at a final state: X → Λ
only when X is a final state.
If a certain state Y is not a final state, we do not include a production of the form : Y → Λ for it.
At every stage in the derivation the working string has this form:
(string of terminals) (one Nonterminal)
until, while in a final state, we apply a production replacing the single nonterminal with Λ. It is important to take careful note of the fact that a path that is not in a final state will be associated with a string that is not all terminals, (i.e. not a word). These correspond to the working strings in the middle of derivations, not to words in the language.
DEFINITION
For a given CFG a semiword is a string of terminals (maybe none) concatenated with exactly one nonterminal (on the right), for example,
(terminal) (terminal) . . . (terminal) (Nonterminal)
Contrast this with word, which is a string of all terminals, and working string, which is a string of any number of terminals and nonterminals in any order.
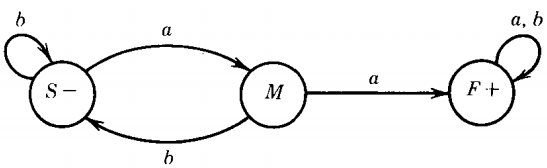
Let us examine next a case of an FA that has two final states. One easy example of this is the FA for the language of all words without double a's. This, the complement of the language of the last example, is also regular and is accepted by the machine FA'.
Let us retain for the moment the names of the nonterminals we had before: S for start, M for middle, and F for what used to be the final state, but is not anymore.
The productions that describe the labels of the edges of the paths are still
S → aM | bS
M → bS | aF
F → aF | bF
as before.
However, now we have a different set of final states. We can accept a string with its path ending in S or M, so we include the productions:
S → Λ
and
M → Λ
but not
F → ΛThe following paragraph is the explanation for why this algorithm works:
Any path through the machine FA' that starts at - corresponds to a string of edge labels and simultaneously to a sequence of productions generating a semiword whose terminal section is the edge label string and whose right-end nonterminal is the name of the state the path ends in. If the path ends in a final state, then we can accept the input string as a word in the language of the machine, and simultaneously finish the generation of this word from the CFG by employing the production:
(Nonterminal corresponding to final state) → Λ
Because our definition of CFG's requires that we always start a derivation with the particular start symbol S, it is always necessary to label the unique start state in an FA with the nonterminal name S.
The rest of the choice of names of states is arbitrary
THEOREM : All regular languages can be generated by CFG's . All regular languages are CFL's.
EXAMPLE
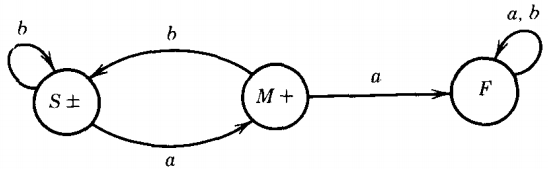
The language of all words with an even number of a's (with at least some a's) is regular since it can be accepted by this FA:
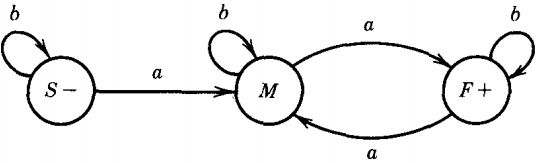
Calling the states S, M, and F as before, we have the following corresponding set of productions:
S → bS | aM
M → bM | aF
F → bF | aM | Λ
We have already seen two CFG's for this language, but this CFG is substantially different. (Here we may ask a fundamental question:
How can we tell whether two CFG's generate the same language? But fundamental questions do not always have satisfactory answers.)
THEOREM
If all the productions in a given CFG fit one of the two forms:
Nonterminal → semiword or Nonterminal → word
(where the word may be Λ) then the language generated by this CFG is regular.
PROOF
We shall prove that the language generated by such a CFG is regular by showing that there is a TG that accepts the same language. We shall build this TG by constructive algorithm.
Let us consider a general CFG in this form:
\( N_1 \rightarrow w_1N_2 ; N_7 \rightarrow W_{10}\\ N_1 \rightarrow w_2N_3 N_{41} \rightarrow W_{23}\\ N_2 \rightarrow w_3N_4 ...\\ \)
where the N's are the nonterminals, the w's are strings of terminals, and the parts wyNz are the semiwords used in productions. One of these N's must be S. Let N1 = S.
Draw a small circle for each N and one extra circle labeled +. The circle for S we label
For every production rule of the form:
\( N_x \rightarrow w_yN_z \)
draw a directed edge from state Nx to Nz, and label it with the word wy.
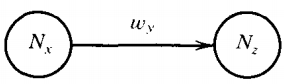
If the two nonterminals above are the same the path is a loop. For every production rule of the form:
\( N_p \rightarrow W_q \)
draw a directed edge from Np to + and label it with the word Wq
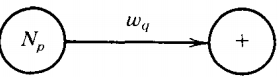
We have now constructed a transition graph. Any path in this TG from - to + corresponds to a word in the language of the TG (by concatenating
labels) and simultaneously corresponds to a sequence of productions in the CFG generating the same word. Conversely, every production of a word in this CFG:
S ⇒ wN ⇒ wwN ⇒ wwwN ... ⇒ wwwww
corresponds to a path in this TG from - to +. Therefore, the language of this TG is exactly the same as the language of the CFG. Therefore, the language of the CFG is regular.
We should note that the fact that the productions in some CFG are all in the required format does not guarantee that the grammar generates any words.
If the grammar is totally discombobulated, the TG that we form from it will be crazy too and accept no words.
However, if the grammar generates a language of some words then the TG produced above for it will accept that language.
DEFINITION
A CFG is called a regular grammar if each of its productions is of one of the two forms
Nonterminal - semiword
or
Nonterminal - wordThe two previous proofs imply that all regular languages can be generated by regular grammars and all regular grammars generate regular languages.
Despite both theorems it is still possible that a CFG that is not in the form of a regular grammar can generate a regular language.
EXAMPLE
Consider the CFG:
S → aaS | bbS | Λ
This is a regular grammar and so we may apply the algorithm to it. There is only one nonterminal, S, so there will be only two states in the TG, - and the mandated +. The only production of the form
\( N_p \rightarrow W_q \)
is
S → Λso there is only one edge into + and that is labeled Λ.
The productions S → aaS and S → bbS are of the form N1 → wN2 where the N's are both S.
Since these are supposed to be made into paths from N1 to N2 they become loops from S back to S.
These two productions will become two loops at - one labeled aa and one labeled bb. The whole TG is shown below:
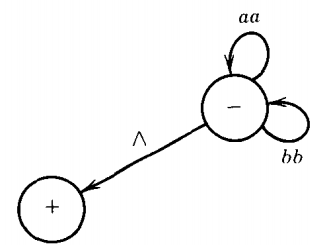
By Kleene's theorem, any language accepted by a TG is regular, therefore the language generated by this CFG (which is the same) is regular.
It corresponds to the regular expression (aa + bb)*
EXAMPLE
Consider the CFG:
S → aaS | bbS | abX | baX | Λ
X → aaX | bbX | abS | baSThe algorithm tells us that there will be three states: -, X, +.
Since there is only one production of the form
Np → Wq
there is only one edge into +. The TG is:
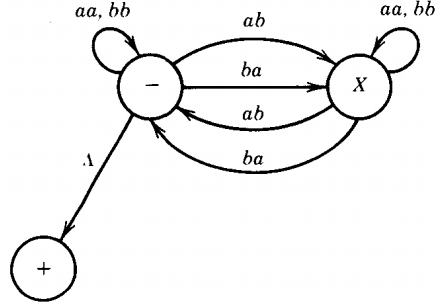
which we immediately see accepts our old friend the language EVEN-EVEN. (Do not be fooled by the A edge to the + state. It is the same as relabeling the - state \( \pm \) )
EXAMPLE
Consider the CFG:
S → aA | bB
A → aS | a
B → bS | bThe corresponding TG constructed by the conversion algorithm is:
The language of this CFG is exactly the same as the language of the CFG two examples ago except that it does not include the word Λ. This language can be defined by the regular expression (aa + bb)+.
We should also notice that the CFG above does not have any productions of the form : Nx → Λ
For a CFG to accept the word Λ, it must have at least one production of this form, called a Λ-production.
A theorem in the next chapter states that any CFL that does not include the word Λ can be defined by a CFG that includes no Λ-productions.
Notice that a Λ-production need not imply that Λ is in the language, as with
S → aX
X → ΛThe language here is just the word a.
The CFG's that are constructed by the conversion algorithm always have Λ-productions, but they do not always generate the word Λ.
We know this because not all regular languages contain the word Λ, but the algorithm suggested in the theorem shows that they can all be converted into CFG's with Λ-productions.