PUSHDOWN AUTOMATA
The class of languages generated by CFG's is properly larger than the class of languages defined by regular expressions.
This means that all regular languages can be generated by CFG's, and so can some nonregular languages (for example, {anbn} and PALINDROME).
After introducing the regular languages defined by regular expressions we found a class of abstract machines (FA's) with the following dual property:
For each regular language there is at least one machine that runs successfully only on the input strings from that language and for each machine in the class the set of words it accepts is a regular language.
We are looking for a mathematical model of some class of machines that correspond analogously to CFL's; that is, there should be at least one machine that accepts each CFL and the language accepted by each machine is context-free.
We want CFL recognizers or CFL-acceptors just as FA's are regular language recognizers and acceptors.
What we shall do first is develop a slightly different pictorial representation for FA's, one that will be easy to augment with the new gizmos.
We have, so far, not given a name to the part of the FA where the input string lives while it is being run. Let us call this the INPUT TAPE.
The INPUT TAPE must be long enough for any possible input, and since any word in a* is a possible input, the TAPE must be infinitely long (such a tape is very expensive).
The TAPE has a first location for the first letter of the input, then a second location, and so on. Therefore, we say that the TAPE is infinite in one direction only.
We draw the TAPE as shown here:

The locations into which we put the input letters are called cells. We name the cells with lowercase Roman numerals.

Below we show an example of an input TAPE already loaded with the input string aaba. The character "△" is used to indicate a blank in a TAPE cell.

The vast majority (all but four) of the cells on the input TAPE are empty, that is, they are loaded with blanks, △△△ . ... As we process this TAPE on the machine we read one letter at a time and eliminate each as it is used.
When we reach the first blank cell we stop. We always presume that once the first blank is encountered the rest of the TAPE is also blank. We read from left to right and never go back to a cell that was read before.
As part of our new pictorial representations for FA's, let us introduce the symbols
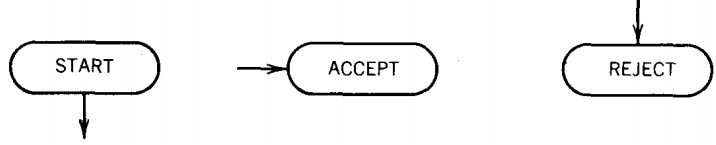
to streamline the design of the machine. The arrows (directed edges) into or out of these states can be drawn at any angle. The START state is like a - state connected to another state in a TG by a Λ edge. We begin the process there, but we read no input letter.
We just proceed immediately to the next state. A start state has no arrows coming into it. An ACCEPT state is a shorthand notation for a dead-end final state-once entered, it cannot be left, such as:
Since we have used the adjective "final" to apply only to accepting states in FA's, we call the new ACCEPT and REJECT states "halt states." Previously we could pass through a final state if we were not finished reading the input data; halt states cannot be traversed.
We can enter an ACCEPT or REJECT state but we cannot exit. We are changing our diagrams of FA's so that every function a state performs is done by a separate box in the picture.
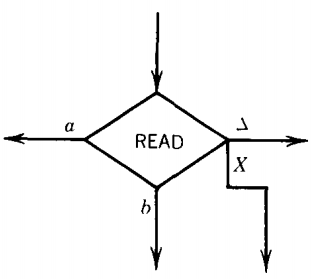
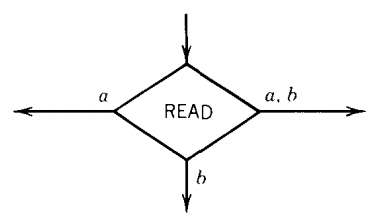
The most important job performed by a state in an FA is to read an input letter and branch to other states depending on what letter has been read.
To do this job from now on we introduce the READ states. These are depicted as diamond shaped boxes as shown below:
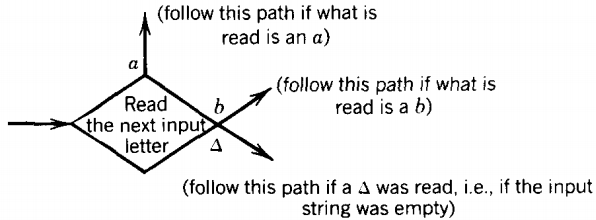
Here again the directions of the edges in the picture above show only one of the many possibilities.
When the character △ is read from the TAPE, it means that we are out of input letters. We are then finished processing the input string.
The △-edge will lead to ACCEPT if the state we have stopped in is a final state and to REJECT if the processing stops in a state that is not a final state.
In our old pictures for FA's we never explained how we knew we were out of input letters.
In these new pictures we can recognize this fact by reading a blank from the TAPE.
These suggestions have not altered the power of our machines. We have merely introduced a new pictorial representation that will not alter their language-accepting abilities.
The FA that used to be drawn like this:
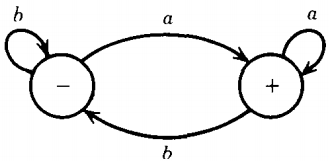
(the FA that accepts all words ending in the letter a) becomes, in the new symbolism, the machine below:
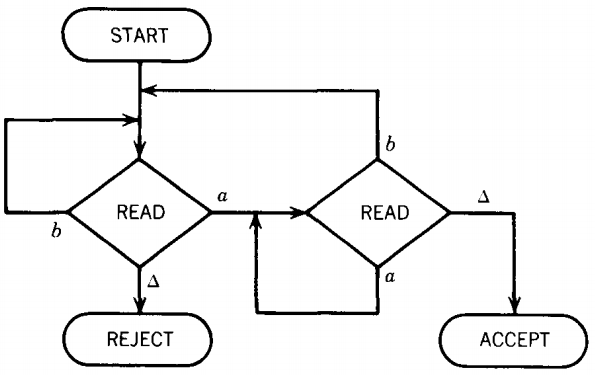
Notice that the edge from START needs no label because START reads no letter.
All the other edges do require labels. We have drawn the edges as straight-line segments, not curves and loops as before.
We have also used the electronic diagram notation for wires flowing into each other. For example,
means
Our machine is still an FA. The edges labeled △ are not to be confused with Λ-labeled edges. These △-edges lead only from READ boxes to halt states.
We have just moved the + and - signs out of the circles that used to indicate states and into adjoining ovals. The "states" are now only READboxes and have no final/nonfinal status.
In the FA above, if we run out of input letters in the left READ state, we will find a △ on the INPUT TAPE and so take the △-edge to REJECT.
Reading a △ in a READ state that corresponds to an FA final state sends us to ACCEPT.
EXAMPLE
becomes
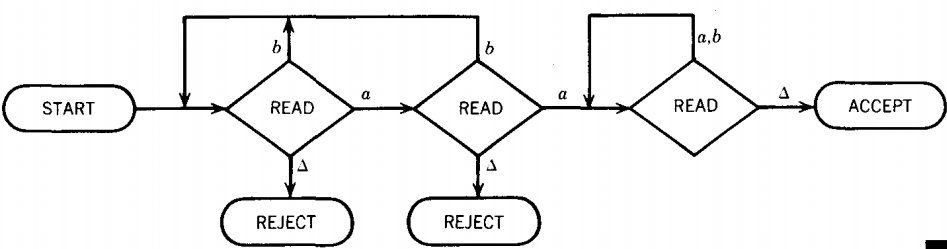
These pictures look more like the "flowcharts" we are familiar with than the old pictures for FA's did.
The general study of the flowchart as a mathematical structure is part of Computer Theory but beyond our intended scope.
The reason we bothered to construct new pictures for FA's (which had perfectly good pictures already) is that it is now easier to make an addition to our machine called the PUSHDOWN STACK or PUSHDOWN STORE.
PUSHDOWN STACK
A PUSHDOWN STACK is a place where input letters (or other information) can be stored until we want to refer to them again.
It holds the letters it has been fed in a long line (as many letters as we want).
The operaton PUSH adds a new letter to the line.
The new letter is placed on top of the STACK, and all the other letters are pushed back (or down) accordingly.
Before the machine begins to process an input string the STACK is presumed to be empty, which means that every storage location in it initially contains a blank.
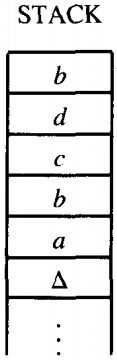
If the STACK is then fed the letters a, b, c, d by this sequence of instructions:
PUSH a
PUSH b
PUSH c
PUSH dthen the top letter in the STACK is d, the second is c, the third is b, and the fourth is a. If we now execute the instruction:
PUSH b
the letter b will be added to the STACK on the top. The d will be pushed down to position 2, the c to position 3, the other b to position 4, and the bottom a to position 5.
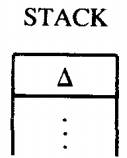
One pictorial representation of a STACK with these letters in it is shown below. Beneath the bottom a we presume that the rest of the STACK, which, like the INPUT TAPE, has infinitely many storage locations, holds only blanks.
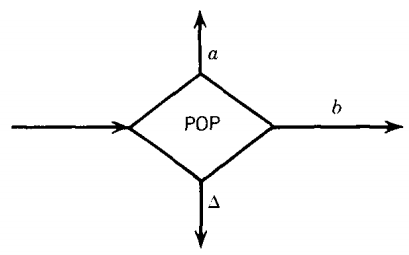
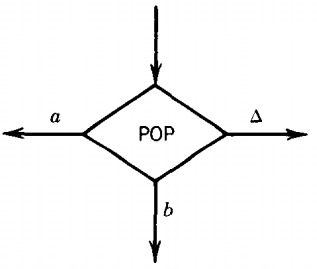
The instruction to take a letter out of the STACK is called POP. This causes the letter on the top of the STACK to be brought out of the STACK
(popped). The rest of the letters are moved up one location each. A PUSHDOWN STACK is called a LIFO file standing for "the LAST IN is the FIRST OUT," like a narrow crowded elevator.
It is not like the normal storage area of a computer, which allows random access (we can retrieve stuff from anywhere regardless of the order in which it was fed in).
A PUSHDOWN STACK lets us read only the top letter.
If we want to read the third letter in the STACK we must go POP, POP, POP, but then we have additionally popped out the first two letters and they are no longer in the STACK.
We also have no simple instruction for determining the bottom letter in the STACK, or for telling how many b's are in the STACK, and so forth.
The only STACK operations allowed to us are PUSH and POP.
Popping an empty STACK, like reading an empty TAPE, gives us the blank character △.
We can add a PUSHDOWN STACK and the operations PUSH and POP to our new drawings of FA's by including as many as we want of the states:
and the states:

The edges coming out of a POP state are labeled in the same way as the edges from a READ state, one (for the moment) for each character that might appear in the STACK including the blank.
Note that branching can occur at POP states but not at PUSH states.
We can leave PUSH states only by the one indicated route, although we can enter a PUSH state from any direction.
When FA's have been souped up with a STACK and POP and PUSH states, we call them pushdown automata, abbreviated PDA's.
The notion of a PUSHDOWN STACK as a data structure had been around for a while, but these mathematicians independently realized that when this structure is incorporated into an FA, its language-recognizing capabilities are increased considerably.
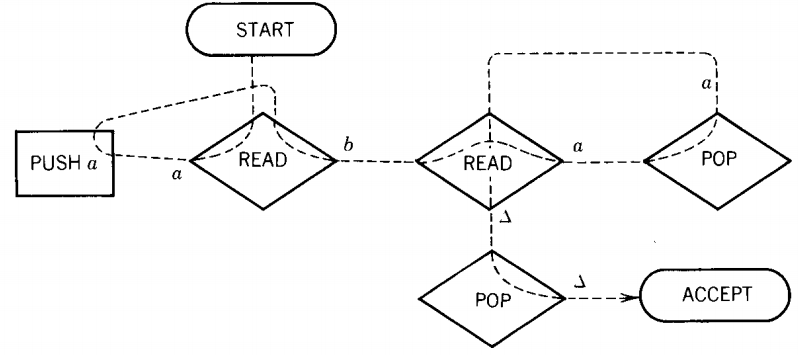
EXAMPLE
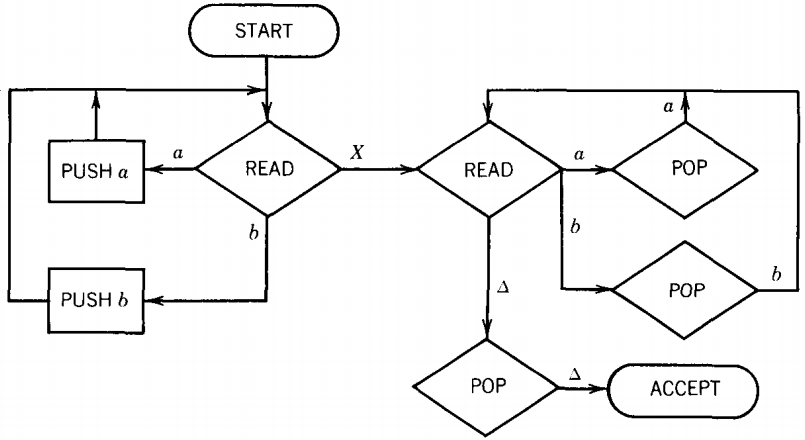
Consider the following PDA:
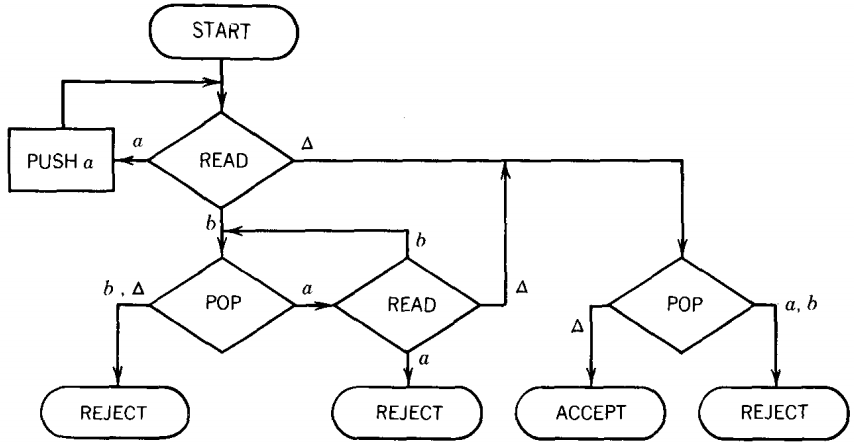
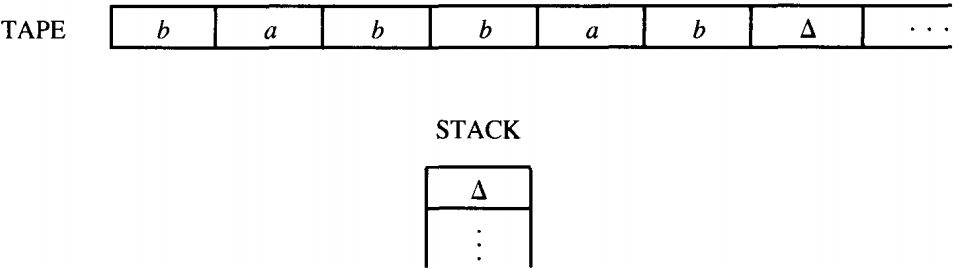
Before we begin to analyze this machine in general, let us see it in operation on the input string aaabbb. We begin by assuming that this string has been put on the TAPE. We always start the operation of the PDA with the STACK empty as shown:
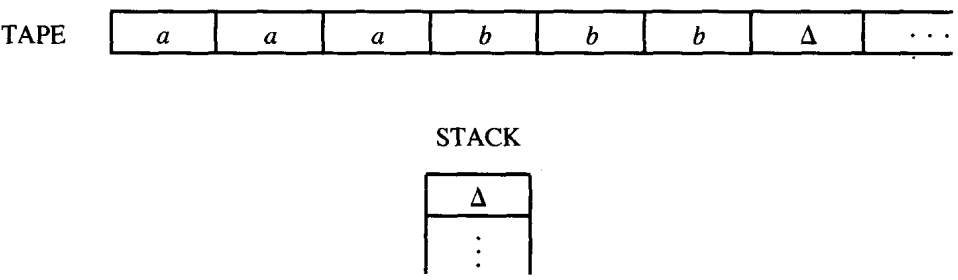
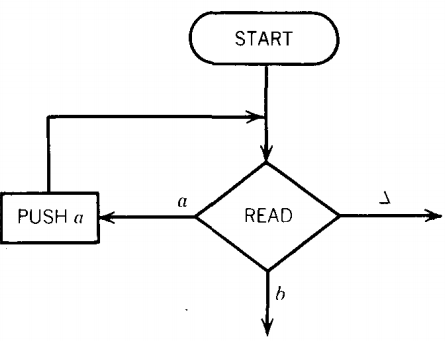
We must begin at START. From there we proceed directly into the upper left READ, a state that reads the first letter of input.
This is an a, so we cross it off the TAPE (it has been read) and we proceed along the a edge from the READ state. This edge brings us to the PUSH a state that tells us to push an a onto the STACK. Now the TAPE and STACK look like this:
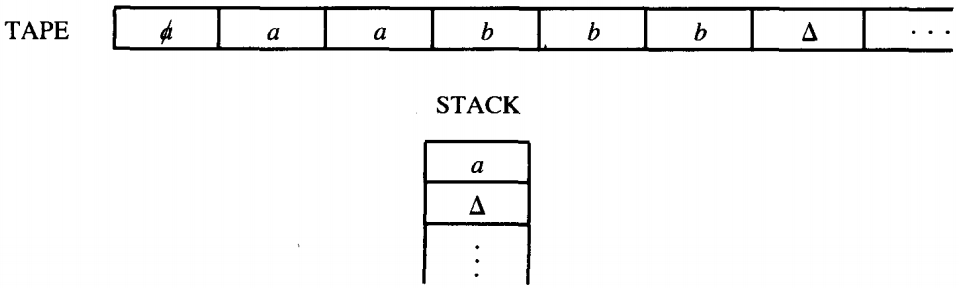
The edge from the PUSH a box takes us back to the line feeding into the same READ box, so we return to this state. We now read another a and proceed as before along the a edge to push it into the STACK. Again we are returned to the READ box.
Again we read an a (our third), and again this a is pushed onto the STACK. The TAPE and STACK now look like this:
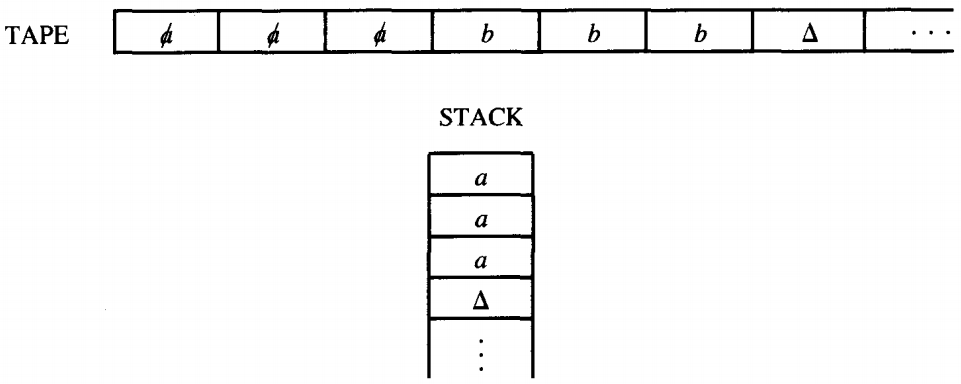
After the third PUSH a, we are routed back to the same READ state again. This time, however, we read the letter b.
This means that we take the b edge out of this state down to the lower left POP. Reading the b leaves the TAPE like this:
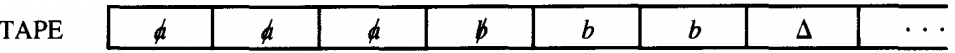
The state POP takes the top element off the STACK. It is an a. It must be an a or a △ since the only letters pushed onto the STACK in the whole program are a's.
If it were a △ or the impossible choice, b, we would have to go to the REJECT state.
However, this time, when we pop the STACK we get the letter a out, leaving the STACK like this:
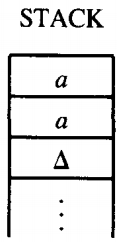
Following the a road from POP takes us to the other READ. The next letter on the TAPE to be read is a b. This leaves the TAPE like this:
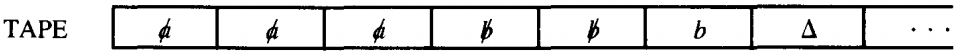
The b road from the second READ state now takes us back to the edge feeding into the POP state. So we pop the STACK again and get another a. The STACK is now down to only one a.
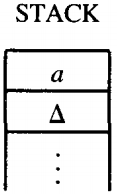
The a line from POP takes us again to this same READ. There is only one letter left on the input TAPE, a b.
We read it and leave the TAPE empty, that is, all blanks.
However, the machine does not yet know that the TAPE is empty. It will discover this only when it next tries to read the TAPE and finds a △.
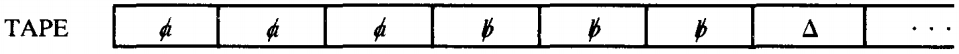
The b that we just read loops us back into the POP state. We then take the last a from the STACK, leaving it also empty-all blanks
The a takes us from POP to the right side READ again. This time the only thing we can read from the TAPE is a blank, △.
The △-edge takes us to the other POP on the right side. This POP now asks us to take a letter from the STACK, but the STACK is empty. Therefore, we say that we pop a △.
This means that we must follow the △-edge, which leads straight to the halt state ACCEPT. Therefore, the word aaabbb is accepted by this machine. More than this can be observed.
The language of words accepted by this machine is exactly: {anbn, n = 0 1 2 ... }
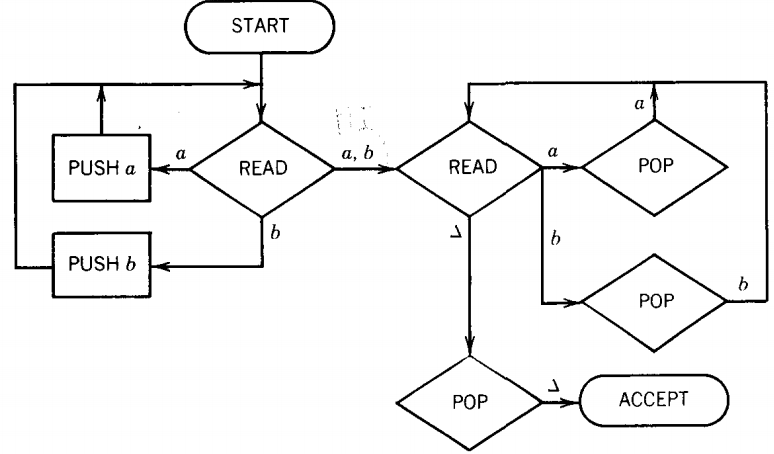
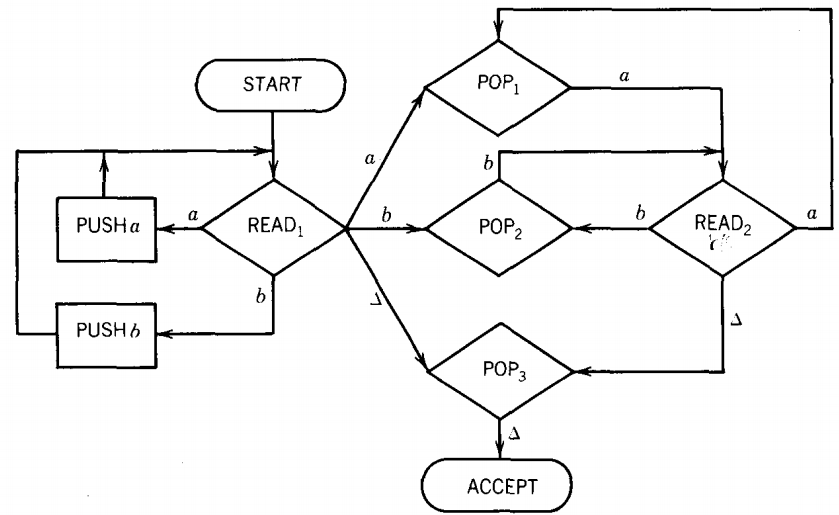
Example
The first part of the machine
is a circuit of states that reads from the TAPE some number of a's in a row and pushes them into the STACK.
This is the only place in the machine where anything is pushed into the STACK.
Once we leave this circuit, we cannot return, and the STACK contains everything it will ever contain.
After we have loaded the STACK with all the a's from the front end of the input string, we read yet another letter from the input TAPE.
If this character is a △, it means that the input word was of the form an, where n might have been 0 (i.e., some word in a*).
If this is the input, we take the △-line all the way to the right-side POP state.
This tests the STACK to see if it has anything in it. If it has, we go to REJECT.
If the STACK is empty at this point, the input string must have been the null word, Λ, which we accept.
Let us now consider the other logical possibility, that after loading the front a's from the input (whether there are many or none) onto the STACK we
read a b. This must be the first b in the input string. It takes us to a new section of the machine into another small circuit.
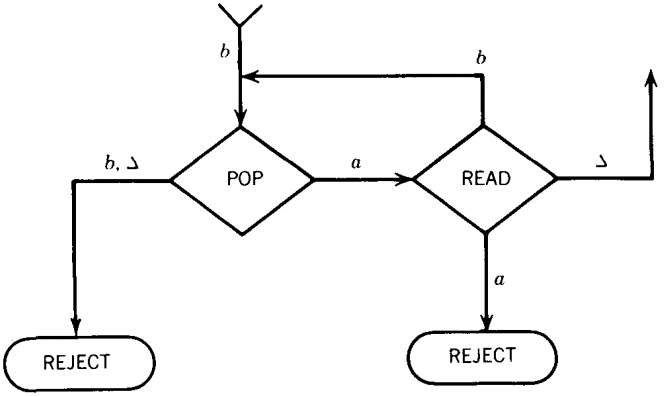
On reading this first b we immediately pop the STACK. The STACK can contain some a's or only △'s.
If the input string started with a b, we would be popping the STACK without ever having pushed anything onto it. We would then pop a △ and go to REJECT.
If we pop a b, something impossible has happened. So we go to REJECT and call the repair person. If we pop an a we go to the lower right READ state that asks us to read a new letter.
As long as we keep popping a's from the STACK to match the b's we are reading from the TAPE, we circle between these two states happily: POP a, READ b, POP a, READ b.
If we pop a △ from the STACK, it means that we ran out of STACK a's before the TAPE ran out of input b's. This △-edge brings us to REJECT.
Since we entered this two-state circuit by reading a b from the TAPE before popping any a's, if the input is a word of the form anbn, then the b's will run out first.
If while looping around this circuit we hit an a on the TAPE, the READ state sends us to REJECT because this means the input is of the form : (some a's) (some b's) (another a) ...
We cannot accept any word in which we come to an a after having read the first b. To get to ACCEPT the second READ state must read a blank and send us to the second POP state. Reading this blank means that the word ends after its clump of b's.
All the words accepted by this machine must therefore be of the form a*b* but, as we shall now see, only some of these words successfully reach the halt state ACCEPT.
Eventually the TAPE will run out of letters and the READ state will turn up a blank.
An input word of the form anbn puts n a's into the STACK. The first b read then takes us to the second circuit.
After n trips around this circuit, we have popped the last a from the STACK and have read the other (n - 1) b's and a blank from the TAPE. We then exit this section to go to the last test.
We have exhausted the TAPE's supply of b's, so we should check to see
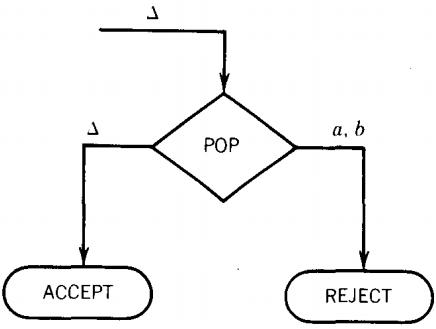
that the STACK is empty. We want to be sure we pop a △, otherwise we reject the word because there must have been more a's in the front than b's in the back.
For us to get to ACCEPT, both TAPE and STACK must empty together. Therefore, the set of words this PDA accepts is exactly the language {anbn, n = 0 1 2 3...}
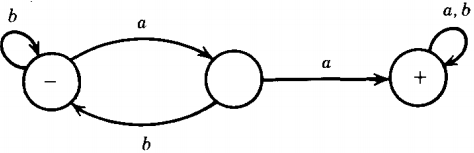
Pushdown automata are more powerful than finite automata
We have already shown that the language accepted by the PDA above could not be accepted by any FA, so pushdown automata are more powerful than finite automata.
We can say more powerful because all regular languages can be accepted by some PDA since they can be accepted by some FA and an FA (in the new notation) is exactly like a PDA that never uses its STACK.
Every CFL can be defined as the language accepted by some PDA and the language accepted by any PDA can be defined by some CFG-a situation exactly analogous to the relationship between regular expressions and FA's-a context-free Kleene's Theorem
What makes these machines more powerful than FA's.
The reason is that even though they too have only finitely many states to roam among, they do have an unlimited capacity for memory.
They can know where they have been, and how often. The reason no FA could accept the language {anbn} was that for large enough n the an part had to run around in a circuit and the machine could not keep track of how many times it had looped around.
It could therefore not distinguish between anbn and some ambn. However, the PDA has a primitive memory unit.
It can keep track of how many a's are read in at the beginning.
It can know how many times a circuit is traversed in general by putting a count cell, PUSH a, inside the loop.
Properties of Pushdown stack
We need not restrict ourselves to using the same alphabet for input strings as we use for the STACK.
In the example above, we could have read an a from the TAPE and then pushed an X into the STACK and let the X's count the number of a's.
In this case, when we test the STACK with a POP state, we branch on X or △. The machine would then look like this:
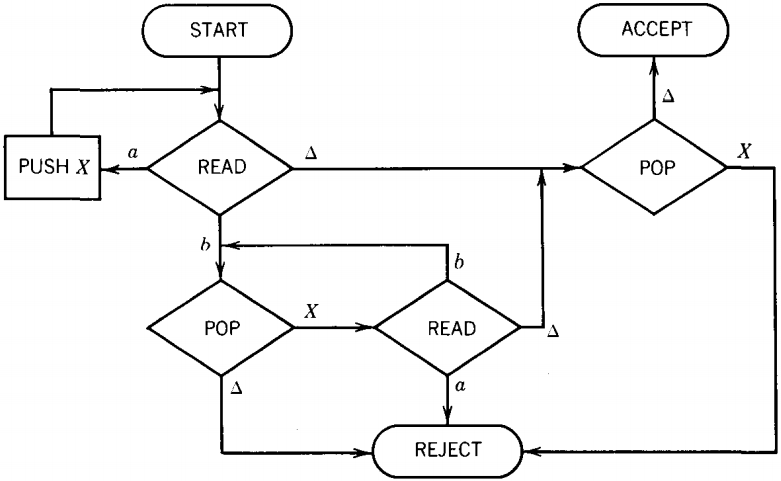
We have drawn this version of the PDA with some minor variations of display but no substantive change in function
The READ states must provide branches for a, b, or △. The POP states must provide branches for X or △.
We eliminated two REJECT states, by having all rejecting edges go into the same state
we should not make the mistake of thinking that the STACK is an output device. It is an internal part of the PDA
The second point that we should discuss is the possibility of nondeterminism.
In our search for the machine equivalent to CFG's we saw that a memory device of some kind is required to accept the language {anbn}.
Is the addition of the STACK enough of a change to allow these new machines to accept all CFL's? Consideration of the language PALINDROME will soon convince us that the new machines (PDA's) will have to be nondeterministic if they are to correspond to CFG's.
Deterministic and Non deterministic PDA
A deterministic PDA is one for which every input string has a unique path through the machine.
A nondeterministic PDA is one for which at certain times we may have to choose among possible paths through the machine.
We say that an input string is accepted by such a machine if some set of choices leads us to an ACCEPT state.
If for all possible paths that a certain input string can follow it always ends at a REJECT state, then the string must be rejected.
This is analogous to the definition of acceptance for TG's, which are also nondeterministic.
As with TG's, nondeterminism here will also allow the possibility of too few as well as too many edges leading from a branch state.
We shall have complete freedom not to put a b-edge leading out of a particular READ state.
If a b is, by chance, read from the INPUT TAPE by that state, processing cannot continue.
As with TG's, we say the machine crashes and the input is rejected.
To have no b edge leading out of a branch state (READ or POP) is the same as having exactly one b-edge that leads straight to REJECT.
The PDA's that are equivalent to CFG's is the class of nondeterministic ones.
For FA's we found that nondeterminism (which gave us TG's and NFA's) did not increase the power of the machine to accept new languages.
For PDA's, this is different. The following Venn diagram shows the relative power of these three types of machines:

EXAMPLE
Let us introduce the PALINDROMEX, language of all words of the form s X reverse(s) where s is any string in (a + b)*.
The words in this language are { X aXa bXb aaXaa abXba baXab bbXbb aaaXaaa aabXbaa . . . }
All these words are palindromes in that they read the same forward and backward.
They all contain exactly one X, and this X marks the middle of the word.
In the first part of the machine the STACK is loaded with the letters from the input string just as the initial a's from anbn were pushed onto the STACK.
Conveniently for us, the letters go into the STACK first letter on the bottom, second letter on top of it, and so on till the last letter pushed in ends up on top.
When we read the X we know we have reached the middle of the input.
We can then begin to compare the front half of the word (which is reversed in the STACK) with the back half (still on the TAPE) to see that they match.
We begin by storing the front half of the input string in the STACK with this part of the machine.
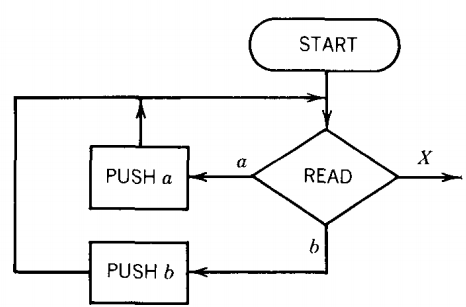
If we READ an a, we PUSH an a. If we READ a b, we PUSH a b, and on and on until we encounter the X on the TAPE.
After we take the first half of the word and stick it into the STACK, we have reversed the order of the letters and it looks exactly like the second half of the word.
For example, if we begin with the input string
abbXbba
then at the moment we are just about to read the X we have:
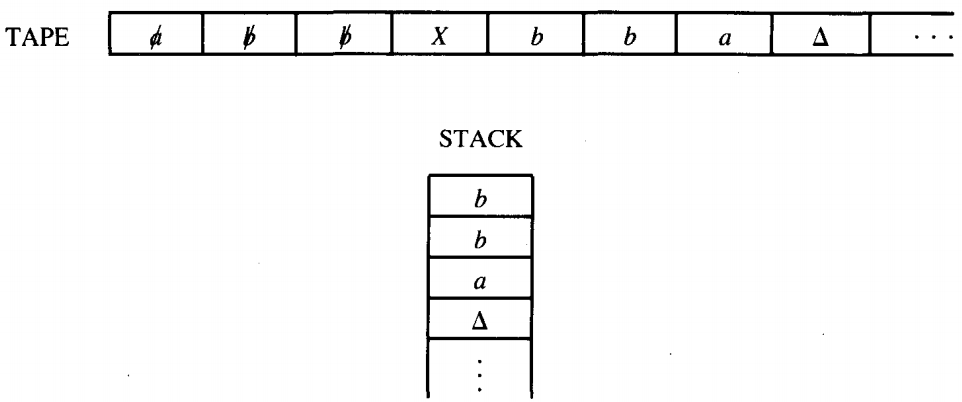
When we read the X we do not put it into the STACK. It is used up in the process of transferring us to phase two. This is where we compare what is left on the TAPE with what is in the STACK. In order to reach ACCEPT, these two should be the same letter for letter, down to the blanks.
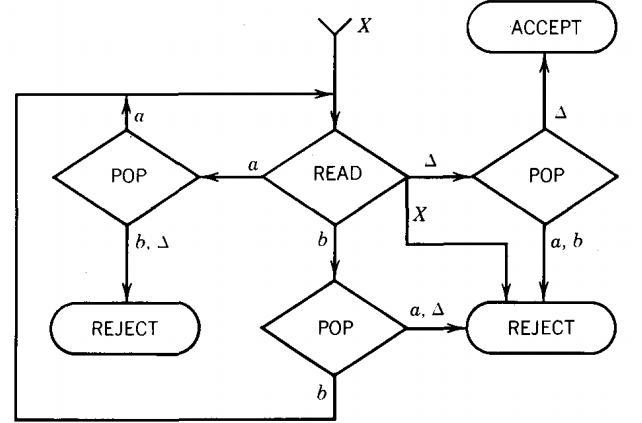
If we read an a, we had better pop an a (pop anything else and we REJECT), if we read a b, we had better pop a b (anything else and we REJECT), if we read a blank, we had better pop a blank; when we do, we accept. If we ever read a second X, we also go to REJECT.
The machine we have drawn is deterministic. The input alphabet here is Σ = {a, b, X}, so each READ state has four edges coming out of it.
The STACK alphabet has two letters F = {a, b}, so each POP has three edges coming out of it:
At each READ and each POP there is only one direction the input can take.
Each string on the TAPE generates a unique path through this PDA.
We can draw a less complicated picture for this PDA without the REJECT states if we do not mind having an input string crash when it has no path to follow.
This means that when we are in a READ or a POP state and find there is no edge with a label corresponding to the character we have just encountered, we terminate processing, reject the input string, and say that the execution crashed.
The whole PDA (without REJECT's) is pictured below:
EXAMPLE
Let us now consider what kind of PDA could accept the language ODDPALINDROME.
This is the language of all strings of a's and b's that are palindromes and have an odd number of letters.
The words in this language are just like the words in PALINDROMEX except that the middle letter X has been changed into an a or a b.
ODDPALINDROME = {a b aaa aba bab bbb. . . }
The problem here is that the middle letter does not stand out, so it is harder to recognize where the first half ends and the second half begins.
A PDA, just like an FA, reads the input string sequentially from left to right and has no idea at any stage how many letters remain to be read.
In PALINDROMEX we knew that X marked the spot; now we have lost that
If we accidentally push into the STACK even one letter too many, the STACK will be larger than what is left on the TAPE and the front and back will not match.
The algorithm we used to accept PALINDROMEX cannot be used without modification to accept ODDPALINDROME.
The algorithm can be altered to fit our needs by introducing one nondeterministic jump.
That we choose this approach does not mean that there is not a completely different method that might work deterministically, but the introduction of nondeterminism here seems quite naturally suited to our purpose.
Consider:
This machine is the same as the previous machine except that we have changed the X into the choice: a or b.
The machine is now nondeterministic since the left READ state has two choices for exit edges labeled a and two choices for b:
If we branch at the right time (exactly at the middle letter) along the former X-edge, we can accept all words in ODDPALINDROME.
If we do not choose the right edge at the right time, the input string will be rejected even if it is in ODDPALINDROME.
Let us recall, however, that for a word to be accepted by a nondeterministic machine (NFA or TG or PDA) all that is necessary is that some choice of edges does lead to ACCEPT.
For every word in ODDPALINDROME, if we make the right choices the path does lead to acceptance.
The word aba can be accepted by this machine if it follows the dotted path.
It will be rejected if it tries to push two, three, or no letters into the STACK before taking the right-hand branch to the second READ state.
EXAMPLE
EVENPALINDROME = {s reverse(s), where s is in (a + b)*}
= { Λ aa bb aaaa abba baab bbbbaaaaaa... }
This is the language of all palindromes with an even number of letters.
One machine to accept this language is pictured below:
We have labeled the READ states 1 and 2 and the POP states 1, 2 and 3 so that we can identify them in discussion. These numbers do not indicate that we are to READ or POP more than one letter. They are only labels.
The names will help us trace the path of an input string through the machine.
This machine is nondeterministic. At READ1 when we read an a from the TAPE we have the option of following an a-edge to PUSH a or an a-edge of POP1
If we read a b in READ1 , we also have two alternatives: to go to PUSH b or to go to POP2. If we read a △ in READ1, we have only one choice: to go to POP3
Let us take notice of what we have done here. In the PDA for PALINDROMEX, the X-edge took us into a second circuit, one that had the form: Read from TAPE → compare with STACK → read from TAPE → compare with STACK .... In this machine, we begin the process of "read from
TAPE → compare with STACK" in READ1 .
The first letter of the second half of the word is read in READ1 , then we immediately go to the POP that compares the character read with what is on top of the STACK.
After this we cycle READ2 → POP → READ2 → POP → ....
It will be easier to understand this machine once we see it in action. Let us run the string babbab. Initially we have:
We can trace the path by which this input can be accepted by the successive rows in the table below:
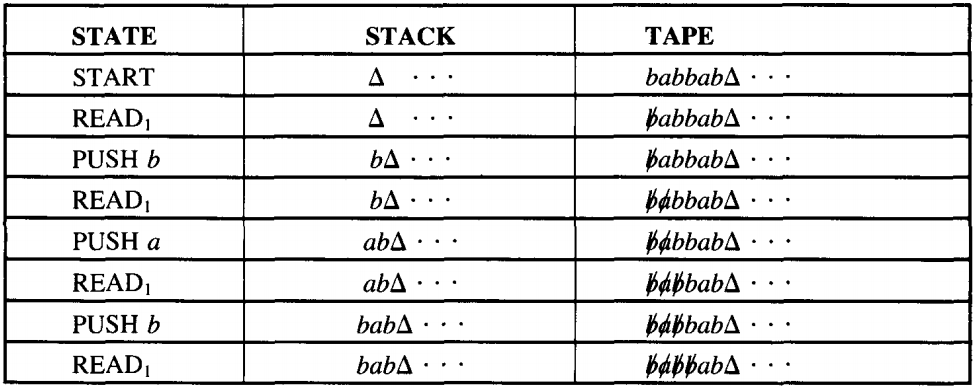
If we are going to accept this input string this is where we must make the jump out of the left circuit into the right circuit. The trace continues
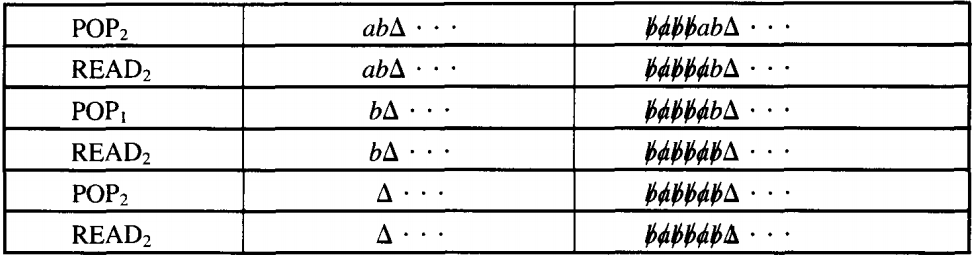
(We have just read the first of the infinitely many blanks on the TAPE.)

Notice that to facilitate the drawing of this table we have rotated the STACK so that it reads left to right instead of top to bottom.
Since this is a nondeterministic machine, there are other paths this input could have taken.
However, none of them leads to acceptance. Below we trace an unsuccessful path.
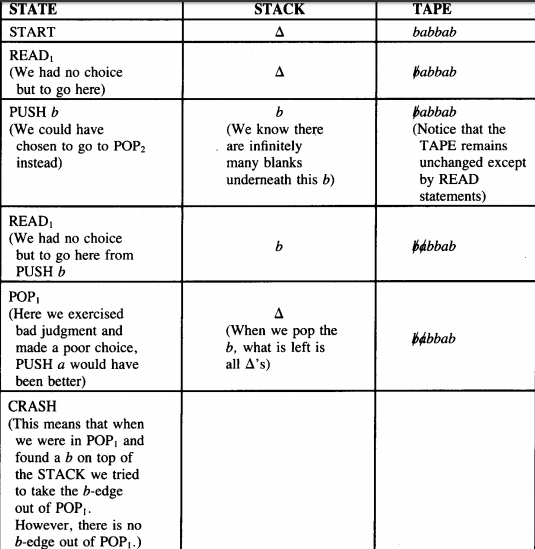
Another unsuccessful approach to accepting the input babbab is to loop around the circuit READ1 → PUSH six times until the whole string has been pushed onto the STACK.
After this, a △ will be read from the TAPE and we have to go to POP3 . This POP will ask if the STACK is empty.
It won't be, so the path will CRASH right here.
The word Λ is accepted by this machine through the sequence:
START → READ → POP3 → ACCEPT
DEFINITION - Pushdown automaton (PDA)
A pushdown automaton, PDA, is a collection of eight things:
An alphabet Σ of input letters.
An input TAPE (infinite in one direction). Initially the string of input letters is placed on the TAPE starting in cell i. The rest of the TAPE is blank.
An alphabet Γ of STACK characters.
A pushdown STACK (infinite in one direction). Initially the STACK is empty (contains all blanks).
One START state that has only out-edges, no in-edges.
Halt states of two kinds: some ACCEPT and some REJECT. They have in-edges and no out-edges
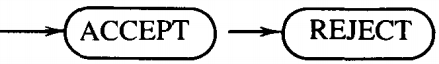
Finitely many nonbranching PUSH states that introduce characters onto the top of the STACK. They are of the form
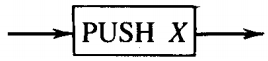
where X is any letter in ΓFinitely many branching states of two kinds:
States that read the next unused letter from the TAPE
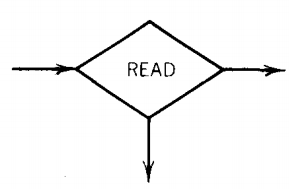
which may have out-edges labeled with letters from Σ and the blank character △, with no restrictions on duplication of labels and no insistance that there be a label for each letter of Σ or △. AndStates that read the top character of the STACK
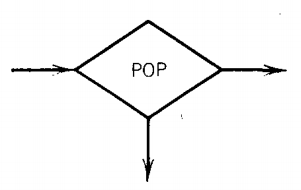
which may have out-edges labeled with the letters of F and the blank character △, again with no restrictions.We further require that the states be connected so as to become a connected directed graph.
To run a string of input letters on a PDA means to begin from the START state and follow the unlabeled edges and those labeled edges that apply (making choices of edges when necessary) to produce a path through the graph.
This path will end either at a halt state or will crash in a branching state when there is no edge corresponding to the letter/character read/popped.
When letters are read from the TAPE or characters are popped from the STACK they are used up and vanish.
An input string with a path that ends in ACCEPT is said to be accepted.
An input string that can follow a selection of paths is said to be accepted if at least one of these paths leads to ACCEPT.
The set of all input strings accepted by a PDA is called the language accepted by the PDA, or the language recognized by the PDA.
EXAMPLE
Consider the language generated by the CFG:
S → S + S | S * S | 4
The terminals are +, *, and 4 and the only nonterminal is S.
The following PDA accepts this language:
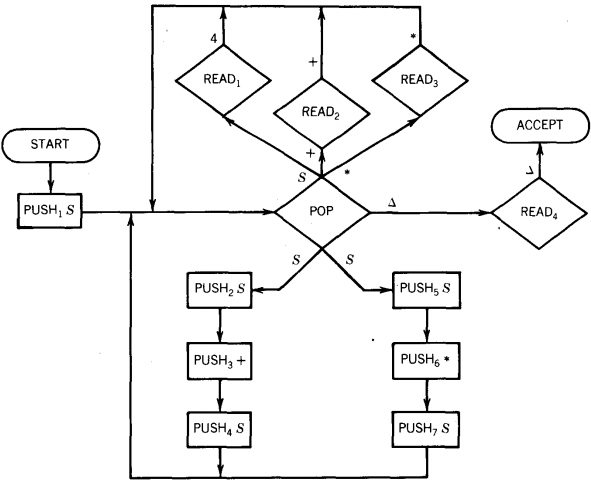
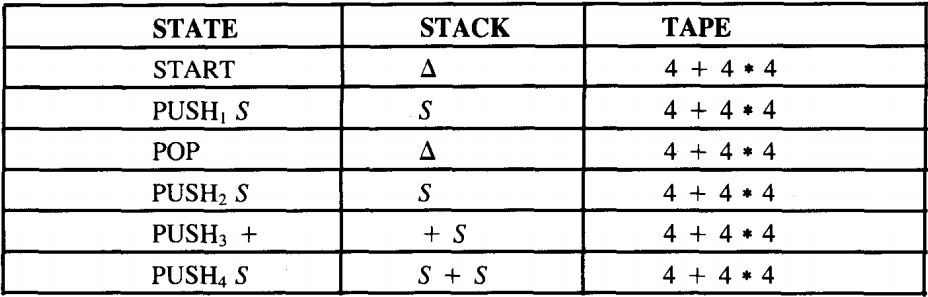
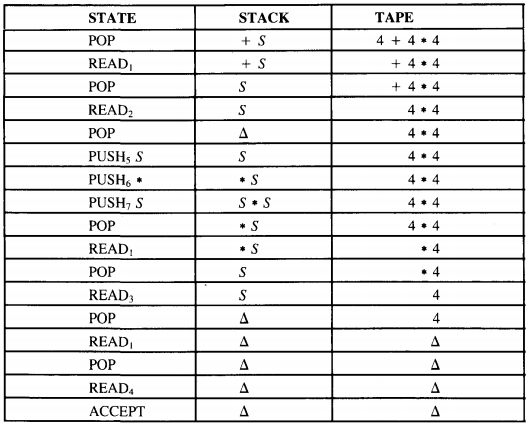
Instead of proving the above machine accepts exactly the language generated by the CFG, we only trace the acceptance of the string.
4 + 4 * 4
This machine offers plenty of opportunity for making nondetermiinistic choices. The path we illustrate is one to acceptance; there are many that fail.
Important difference between a PDA and an FA
One important difference between a PDA and an FA is the length of the path formed by a given input.
If a string of seven letters is fed into an FA, it follows a path exactly seven edges long. In a PDA, the path could be longer or shorter.
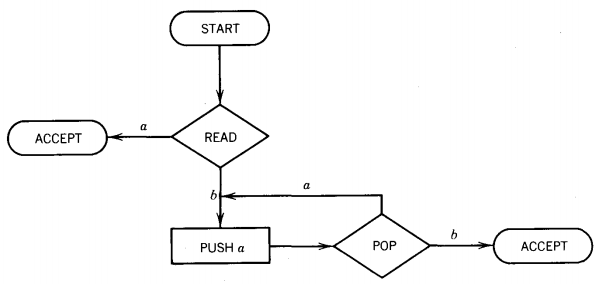
The PDA below accepts the regular language of all words beginning with an a. But no matter how long the input string, the path is only one or two edges long.

Since we can continue to process the blanks on the TAPE even after all input letters have been read, we can have arbitrarily long or even infinite paths caused by very short input words.
For example, the following PDA accepts only the word b, but it must follow a seven-edge path to acceptance:
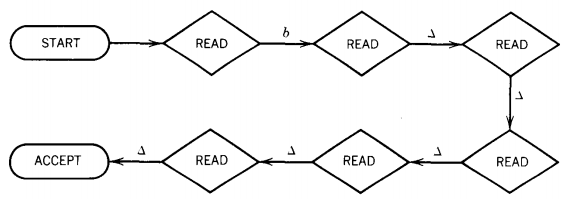
The following machine accepts all words that start with an a in a path of two edges and loops forever on any input starting with a b. (We can consider this an infinite path if we so desire.)
THEOREM
Given any PDA, there is another PDA that accepts exactly the same language with the additional property that whenever a path leads to ACCEPT the STACK and the TAPE contain only blanks.
PROOF
We present a constructive algorithm that will convert any PDA into a PDA with the property mentioned. Whenever we have the machine part:
we replace it with the diagram below:
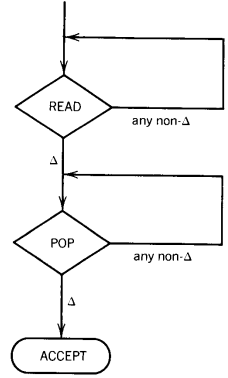
Technically speaking, we should have labeled the top loop "Any letter in Σ" and the bottom loop "any character in Γ"
The new PDA formed accepts exactly the same language and finishes all successful runs with empty TAPE and empty STACK.