NON-CONTEXT-FREE LANGUAGES
To prove this we have to make a very careful study of the mechanics of word production from grammars. Let us consider a CFG that is in Chomsky normal form. All of its productions are of the form:
Nonterminal → Nonterminal Nonterminal
or else
Nonterminal → terminalLet us, for the moment, abandon the disjunctive BNF notation: N → ... | ... | ...
and instead write each production as a separate line and number them:
PROD 1 N → ...
PROD 2 N → ...
PROD 3 N → ...
..... ...In the process of a particular left-most derivation for a particular word in a context-free language, we have two possibilities:
1. No production has, been used more than once.
2. At least one production has been repeated.
Every word with a derivation that satisfies the first possibility can be defined by a string of production numbers that has no repetitions.
Since there are only finitely many productions to begin with, there can be only finitely many words of this nature.
For example, if there are 106 productions,
PROD 1
PROD 2
PROD 3
...
PROD 106then there are exactly 106! possible permutations of them.
Some of these sequences of productions when applied to the start symbol S will lead to the generation of a word by left-most derivation and some (many) will not.
Suppose we start with S and after some partial sequence of applications of productions we arrive at a string of all terminals.
Since there is no left-most nonterminal, let us say that the remaining productions that we may try to apply leave this word unchanged.
We are considering only left-most derivations. If we try to apply a production with a left-side nonterminal that is not the same as the left-most nonterminal in the working string, the system crashes-the sequence of productions does not lead to a word.
For example, consider the CFG for EVENPALINDROME:
PROD S → aSa
PROD 2 S → bSb
PROD 3 S → ΛAll possible permutations of the three productions are:
Prod 1 S ⇒ aSa Prod 1 S ⇒ aSa Prod 2 ⇒ abSba Prod 3 ⇒ aa Prod 3 ⇒ abba Prod 2 ⇒ aa Prod 2 ⇒ bSb Prod 2 ⇒ bSb Prod 1 ⇒ baSab Prod 3 ⇒ bb Prod 3 ⇒ baab Prod 1 ⇒ bb Prod 3 ⇒ Λ Prod 3 ⇒ Λ Prod 1 ⇒ Λ Prod 2 ⇒ Λ Prod 2 ⇒ Λ Prod 1 ⇒ Λ The only words in EVENPALINDROME that can be generated without repetition of production are Λ, aa, bb, abba, and baab. Notice that aaaa, which is just as short as abba, cannot be produced without repeating PROD 1.
In general, not all sequences of productions lead to left-most derivations. For example, consider the following CFG for the language ab*:
PROD 1 S ⇒ XY
PROD 2 X ⇒ a
PROD 3 Y ⇒ bY
PROD 4 Y ⇒ ΛOnly productions with a left side that is S can be used first. The only possible first production in a left-most derivation here is PROD 1.
After this, the left-most nonterminal is X, not Y, so that PROD 3 does not apply yet.
The only sequences of productions (with no production used twice) that lead to words in this case are:
Prod 1 S ⇒ XY Prod 1 S ⇒ XY Prod 2 ⇒ aY Prod 2 ⇒ aY Prod 3 ⇒ abY Prod 4 ⇒ a Prod 4 ⇒ ab Prod 3 ⇒ a So the only words in this language that can be derived without repeated productions are a and ab.
THEOREM
Let G be a CFG in Chomsky normal form. Let us call the productions of the form:
Nonterminal → Nonterminal Nonterminal
live and the productions of the form:
Nonterminal → terminal
dead.
There are only finitely many words in the language generated by G with a left-most derivation that does not use any of the live productions at least twice.
In other words, if we are restricted to using the live productions at most once each, we can generate only finitely many words by left-most derivations.
PROOF
The question we shall consider is: How many nonterminals are there in the working strings at different stages in the production of a word? Suppose we start (in some abstract CFG in CNF that we need not specify) with:
S → AB
The right side, the working string, has exactly two nonterminals. If we apply the live production:
A → XY
we get:
⇒ XYBwhich has three nonterminals. Now applying the dead production:
X → b
we get:
⇒ bYBwith two nonterminals. But now applying the live production:
Y → SX
we get:
⇒ bSXB with three nonterminals again.Every time we apply a live production we increase the number of nonterminals by one.
Every time we apply a dead production we decrease the number of nonterminals by one.
Since the net result of a derivation is to start with one nonterminal, S, and end up with none (a word of solid terminals), the net effect is to lose a nonterminal.
Therefore, in all cases, to arrive at a string of only terminals, we must apply one more dead production than live production.
For example (again these derivations are in some arbitrary, uninteresting CFG's in CNF),
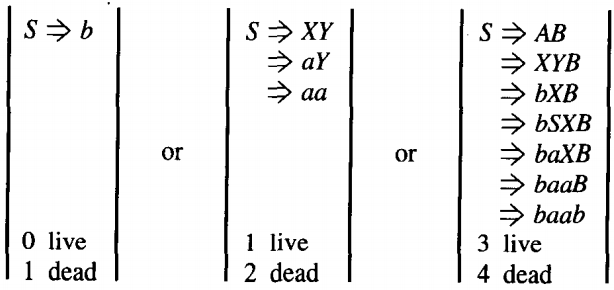
Let us suppose that the grammar G has exactly
p live productions
and
q dead productionsSince any derivation that does not reuse a live production can have at most p live productions, it must have at most (p + 1) dead productions.
Each letter in the final word comes from the application of some dead production.
Therefore, all words generated from G without repeating any live productions have at most (p + 1) letters in them.
Therefore, we have shown that the words of the type described in this theorem cannot be more than (p + 1) letters long.
Therefore, there can be at most finitely many of them.
Suppose that a left-most Chomsky derivation used the same live production twice. What would be the consequences?
Let us start with a CFG for the language NONNULLPALINDROME: S → aSa | bSb | a | b | aa | bb
We can easily see that all palindromes except Λ can be generated from this grammar. We "Chomsky-ize" it as follows:
Original Form Form after conversion CNF S → aSa
S → bSb
S → a
S → b
S → aa
S → bb
A → a
B → b
S → ASA
S → BSB
S → a
S → b
S → AA
S → BB
S → AX
X → SA
S → BY
Y → SB
S → AA
S → BB
S → a
S → b
A → a
B → b
The left-most derivation of the word abaaba in this grammar is:
S ⇒ AX
⇒ aX
⇒ a SA
⇒ a BYA
⇒ ab YA
⇒ ab SBA
⇒ ab AABA
⇒ aba ABA
⇒ abaa BA
⇒ abaab A
⇒ abaabaWhen we start with a CFG in CNF, in all left-most derivations, each intermediate step is a working string of the form: = (string of solid terminals) (string of solid Nonterminals)
This is a special property of left-most Chomsky working strings.
To emphasize this separation of the terminals and the nonterminals in the derivation above, we have inserted a meaningless space between the two substrings.
Let us consider some arbitrary, unspecified CFG in CNF
Suppose that we employ some live production, say, Z → XY
twice in the derivation of some word w in this language. That means that at one point in the derivation, just before the duplicated production was used the first time, the left-most Chomsky working string had the form ⇒ (S1) Z (S2)
where s1 is a string of terminals and S2 is a string of nonterminals. At this point the left-most nonterminal is Z.
We now replace this Z with XY according to the production and continue the derivation.
Since we are going to apply this production again at some later point, the left-most Chomsky working string will sometime have the form: ⇒ (S1) (S3) Z (S4)
where s1 is the same string of terminals unchanged from before (once the terminals have been derived in the front they stay put, nothing can dislodge them) s3 is a newly formed string of terminals, and s4 is the string of nonterminals remaining. We are now about to apply the production Z - XY for the second time.
Where did this second Z come from? Either the second Z is a tree descendant of the first Z or else it comes from something in the old s2 . By the phrase "tree descendant" we mean that in the derivation tree there is an everdownward path from one Z to the other.
Let us look at an example of each possibility
Case 1. Let us consider an arbitrary grammar: S → AZ
Z → BB
B → ZA
A → a
B → bas we proceed with the derivation of some word we find:
S ⇒ AZ
⇒ aZ
⇒ aBB
⇒ abB
⇒ abZA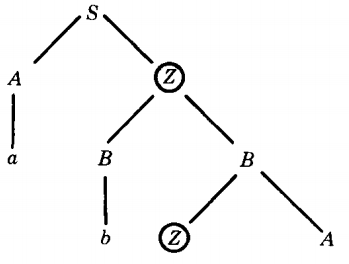
As we see from the derivation tree, the second Z was derived (descended) from the first. We can see this from the diagram because there is a downward path from the first Z to the second. On the other hand we could have something like this.
Case 2. In the arbitrary grammar: S → AA
A → BC
C → BB
A → a
B → bas we proceed with the derivation of some word we find: S ⇒ AA
⇒ BCA
⇒ bCA
⇒ bBBA
Two times the left-most nonterminal is B, but the second B is not descended from the first B in the tree. There is no downward path from the first B to the second B.
THEOREM
If G is a CFG in CNF that has
p live productions
and
q dead productionsand if w is a word generated by G that has more than 2P letters in it, then somewhere in every derivation tree for w there is an example of some nonterminal (call it Z) being used twice as the left-most nonterminal where the second Z is descended from the first Z.
PROOF
Why did we include the arithmetical condition that: length(w) > 2p?
This condition ensures that the production tree for w has more than p rows (generations). This is because at each row in the derivation tree the number of symbols in the working string can at most double.
For example, in some abstract CFG in CNF we may have a derivation tree that looks like this:
(In this figure the nonterminals are chosen completely arbitrarily.) If the bottom row has more than 2P letters, the tree must have more than p + 1 rows.
Let us consider the last terminal that was one of the letters formed on the bottom row of the derivation tree for w by a dead production, say, X → b
The letter b is not necessarily the right-most letter in w, but it is a letter formed after more than p generations of the tree. That means it has more than p direct ancestors up the tree.
From the letter b we trace our way back up through the tree to the top, which is the start symbol S. In this backward trace we encounter one nonterminal after another in the inverse order in which they occurred in the derivation.
Each of these nonterminals represents a production. If there are more than p rows to retrace, then there have been more than p productions in the ancestor path from b to S.
But there are only p different live productions possible in the grammar G; so if more than p have been used in this ancestor-path, then some live productions have been used more than once.
The nonterminal on the left side of this repeated live production has the property that it occurs twice (or more) on the descent line from S to b. This then is a nonterminal that proves our theorem.
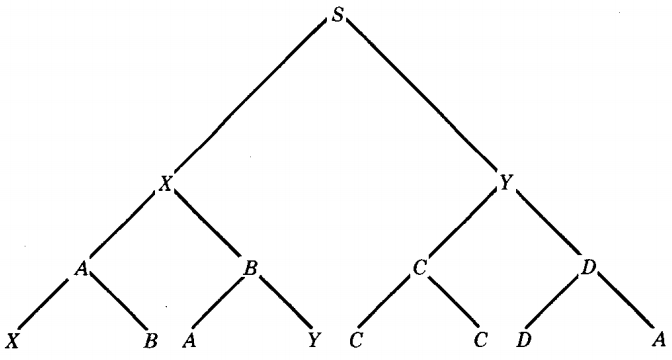
Before stamping the end-of-proof box, let us draw an illustration, a totally arbitrary tree for a word w in a grammar we have not even written out:
The word w is babaababa. Let us trace the ancestor-path of the circled terminal a from the bottom row up.
a came from Y by the production Y → a
Y came from X by the production X → BY
X came from S by the production S → XY
S came from B by the production B → SX
B came from X by the production X → BY
X came from S by the production S → XY
If the ancestor chain is long enough, one production must be used twice. In this example, X → BY is used twice and S → XY is used twice.
The two X's that have boxes drawn around them satisfy the conditions of the theorem. One of them is descended from the other in the derivation tree of w
DEFINITION and Example
In a given derivation of a word in a given CFG a nonterminal is said to be self-embedded if it ever occurs as a tree descendant of itself.
in any CFG all sufficiently long words have left-most derivations that include a self-embedded nonterminal.
Example :
Consider the CFG for NONNULLPALINDROME
S → AX
X → SA
S → BY
Y → SB
S → a
S → b
S → AA
S → BB
A → a
B → b
There are six live productions, so, according to Theorem 34, it would require a word of more than 26 = 64 letters to guarantee that each derivation has a self-embedded nonterminal in it.
If we are only looking for one example of a self-embedded nonterminal we can find such a tree much more easily than that. Consider this derivation tree for the word aabaa
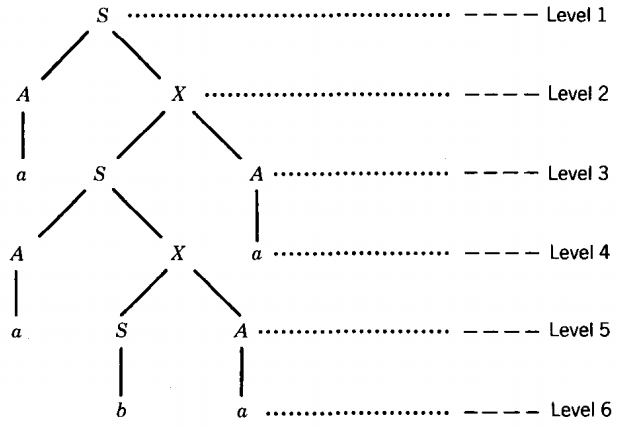
This tree has six levels, so it cannot quite guarantee a self-embedded nonterminal, but it has one anyway. Let us begin with the b on level 6 and trace its path back up to the top:
"The b came from S which came from X, which came from S, which came from X, which came from S".
In this way we find that the production X → SA was used twice in this tree segment:
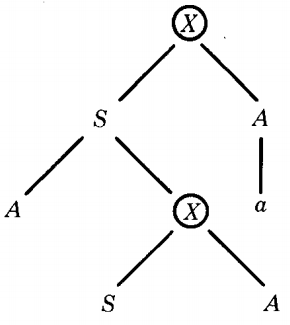
Self-embedded nonterminal
The self-embedded nonterminal that we find in the example above, using is not just a nonterminal that is descended from itself.
It is a nonterminal, say Z, that was replaced by a certain production that later gave birth to another Z that was also replaced by the same production in the derivation of the word.
Specifically, the first X was replaced by the production X → SA and so was its descendant.
We can use this fact, with the self-embedded X's in this example to make some new words.
The tree above proceeds from S down to the first X. Then from the second X the tree proceeds to the final word.
But once we have reached the second X, instead of proceeding with the generation of the word as we have it here, we could instead have repeated the same sequence of productions that the first X initiated, thereby arriving at a third X.
The second can cause the third exactly as the first caused the second. From this third X we could proceed to a final string of all terminals in a manner exactly as the second X did.
The first X can start a subtree that produces the second X, and the second X can start a subtree that produces all terminals, but it does not have to.
Instead the second can begin a subtree exactly like the first's. This will then produce a third X. From this third X we can produce a string of all terminals as the second X used to.
Self-embedded nonterminal example
Suppose we have these productions in a nonsense CFG to illustrate the point.
S → AB
S → BC
A → BA
C → BB
B → AB
A → a
B → b
C → bOne word that has a self-embedded nonterminal is aabab.
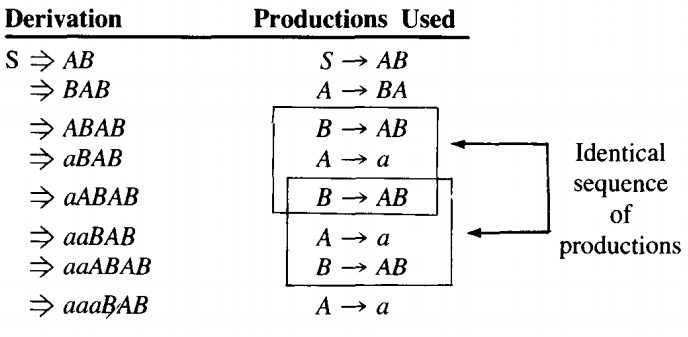
From line 2 to line 3 we employed the production B → AB. This same production is employed from line 4 to line 5. Not only that, but the second left-most B is a descendant of the first.
.Therefore, we can make new words in this language by repeating the sequence of productions used in lines 3, 4, and 5 as if the production for line 5 was the beginning of the same sequence again:
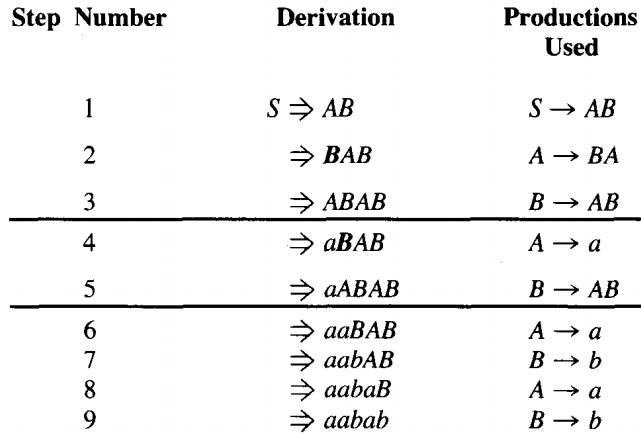
⇒ aaabAB B → b ⇒ aaabaB A → a ⇒ aaabab B → b The sequence can be repeated as often as we wish.
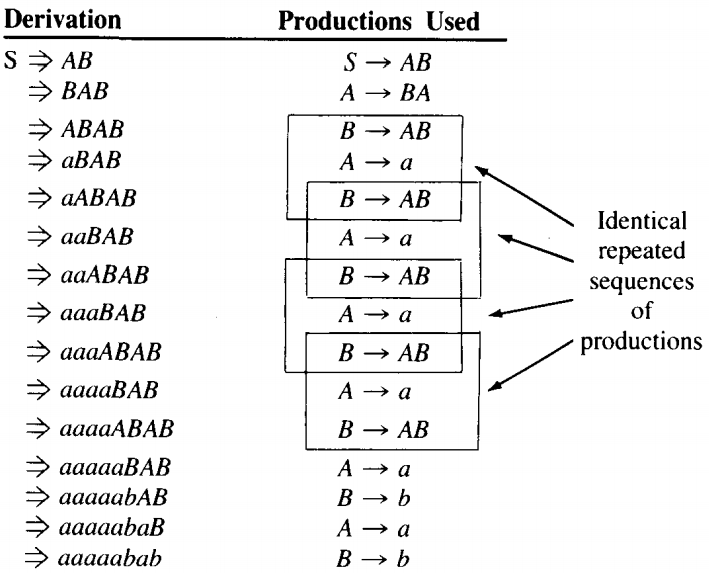
This repetition can be explained in tree diagrams as follows. What is at first .....
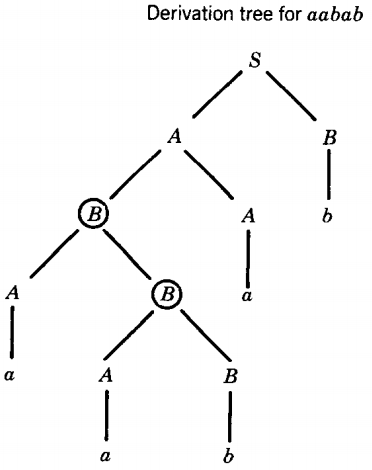
can become
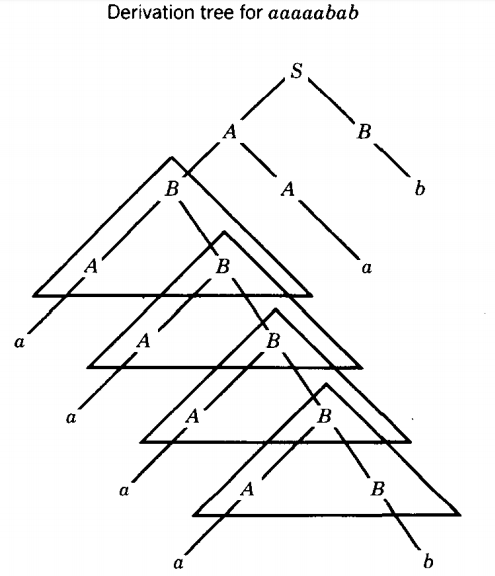
Even though the self-embedded nonterminals must be along the same descent line in the tree, they do not have to be consecutive nodes but may be more distant relatives.
Self-embedded nonterminal example
For the arbitrary CFG
S → AB
A → BC
C → AB
A → a
B → b
One possible derivation tree is
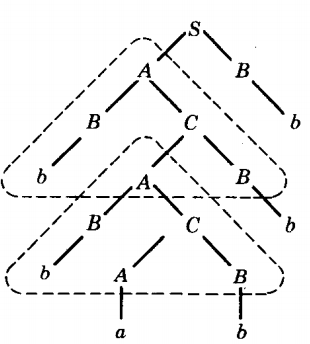
In this case we find the self-embedded nonterminal A in the dotted triangle. Not only is A self-embedded, but it has already been used twice the same way (two identical dotted triangles).
Again we have the option of repeating the sequence of productions in the triangle as many times as we want.
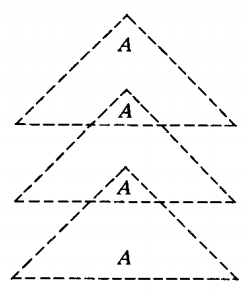
This is why in the last theorem it was important that the repeated nonterminals be along the same line of descent
THEOREM
If G is any CFG in CNF with p live productions and w is any word generated by G with length greater than 2P, then we can break w up into five substrings:
w = u v x y z
such that x is not Λ and v and y are not both Λ and such that all the words
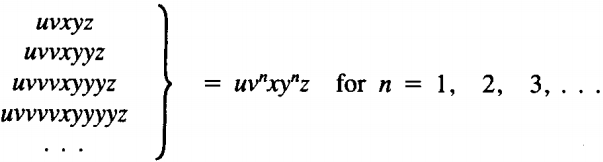
can also be generated by G.
EXAMPLE
We shall analyze a specific case in detail and then consider the situation in its full generality. Let us consider the following CFG in CNF:
S → PQ
Q → QS | b
P → a
The word abab can be derived from these productions by the following derivation tree.
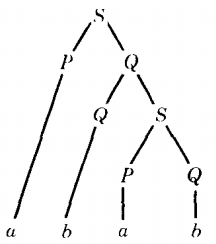
Here we see three instances of self-embedded nonterminals. The top S has another S as a descendant.
The Q on the second level has two Q's as descendants, one on the third level and one of the fourth level.
Notice, however, that the two P's are not descended one from the other, so neither is selfembedded.
For the purposes of our example, we shall focus on the self-embedded Q's of the second and third levels, although it would be just as good to look at the self-embedded S's.
The first Q is replaced by the production Q → QS, while the second is replaced by the production Q → b.
Even though the two Q's are not replaced by the same productions, they are self-embedded and we can apply the technique of this theorem.
If we draw this diagram:
S ⇒ PQ
⇒ aQ
⇒ aQS
⇒ abS
⇒ abPQ
⇒ abaQ
⇒ ababwe can see that the word w can be broken into the five parts uvxyz as follows
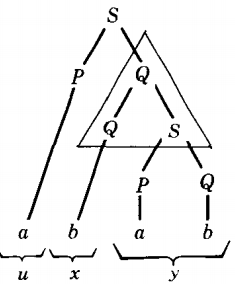
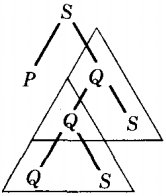
We have located a self-embedded nonterminal Q and we have drawn a triangle enclosing the descent from Q to Q.
The u-part is the part generated by the tree to the left of the triangle. This is only the letter a. The v-part is the substring of w generated inside the triangle to the left of the repeated nonterminal.
Here, however, the repeated nonterminal Q, is the left-most character on the bottom of the triangle. Therefore, v = Λ.
The x-part is the substring of w descended directly from the second occurrence of the repeated nonterminal (the second Q). Here that is clearly the single letter b.
The y-part is the rest of w generated inside the triangle, that is, whatever comes from the triangle to the right of the repeated nonterminal.
In this example this refers to everything that descends from the second S, which is the only thing at the bottom of the triangle to the right of the Q.
What is descended from this S is the substring ab. The z-part is all that is left of w, that is, the substring of w that is generated to the right of the triangle. In this case, that is nothing, z = Λ.
u = a v = Λ x= b y = ab z = Λ
The following diagram shows what would happen if we repeated the triangle from the second Q just as it descends from the first Q.
If we now fill in the picture by adding the terminals that descend from the P, the Q, and the S's, as we did in the original tree, we complete the new derivation tree as follows.
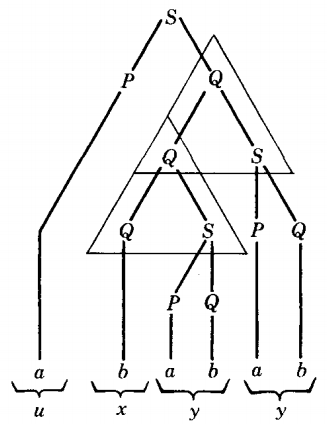
Here we can see that the repetition of the triangle does not effect the upart. There was one u-part and there still is only one u-part. If there were a z-part, that too would be left alone, since these are defined outside the triangle.
There is no v-part in this example, but we can see that the y-part (its right-side counterpart) has become doubled. Each of the two triangles generates exactly the same y-part.
In the middle of all this the x-part has been left alone. There is still only one bottom repeated nonterminal from which the x-part descends. The word with this derivation tree can be written as uvvxyyz.
u v v x y y z = a Λ Λ b a b a b Λ =ababab
If we had tripled the triangle instead of only doubling it, we would obtain
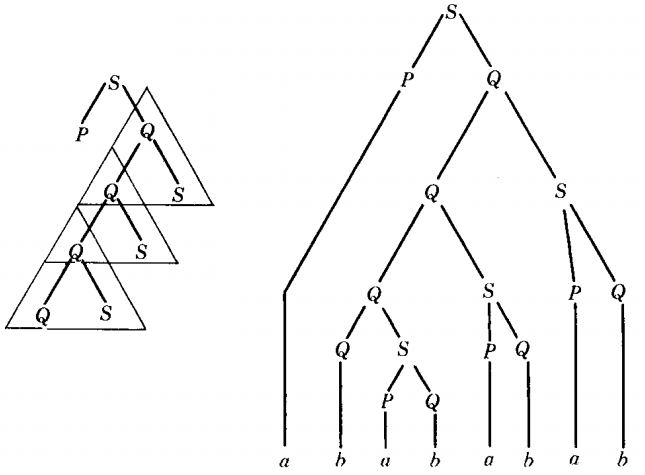
This word we can easily recognize as
u v v v x y y y z = a Λ Λ Λ b ab ab ab Λ
In general, after n occurrences of the triangle we obtain a derivation of the word : u vn x yn z
EXAMPLE
Let us consider the language: {anbnan for n = 1 2 3 ... = {aba aabbaa aaabbbaaa... }
Let us think about how this language could be accepted by a PDA. As we read the first a's, we must accurately store the information about exactly how many a's there were, since a100b99a99 must be rejected but a99b99a99 must be accepted.
We can put this count into the STACK. One obvious way is to put the a's themselves directly into the STACK, but there may be other way' of doing this.
Next we read the b's and we have to ask the STACK if the number of b's is the same as the number of a's.
The problem is that asking the STACK this question makes the STACK forget the answer afterward, since we pop stuff out and cannot put it back until we see that the STACK is empty.
There is no temporary storage possible for the information that we have popped out.
The method we used to recognize the language {anbn} was to store the a's in the STACK and then destroy them one-for-one with the b's. After we have checked that we have the correct number of b's, the STACK is empty. No record remains of how many a's there were originally.
Therefore, we can no longer check whether the last clump of a's in anbnan is the correct size. In answering the first question, the information was lost. This STACK is like a student who forgets the entire course after the final exam.
All we have said so far is, "We don't see how this language can be contextfree since we cannot think of a PDA to accept it." This is, of course, no proof. Maybe someone smarter can figure out the right PDA.
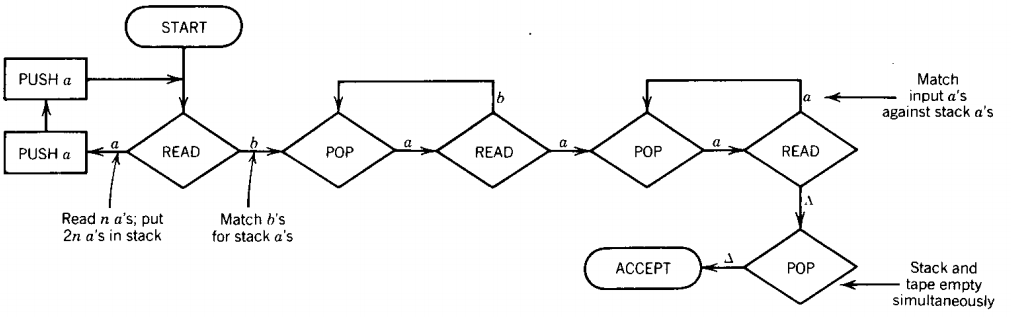
Suppose we try this scheme. For every a we read from the initial cluster we push two a's into the STACK. Then when we read b's we match them against the first half of the a's in the STACK.
When we get to the last clump of a's we have exactly enough left in the STACK to match them also. The proposed PDA is this.
The problem with this idea is that we have no way of checking to be sure that the b's use up exactly half of the a's in the STACK. Unfortunately, the word a10b8a12 is also accepted by this PDA.
The first 10 a's are read and 20 are put into the STACK. Next 8 of these are matched against b's. Lastly, the 12 final a's match the a's remaining in the STACK and the word is accepted even though we do not want it in our language.
The truth is that nobody is ever going to build a PDA that accepts this language. This can be proven using the Pumping Lemma. In other words, we can prove that the language {anbnan} is non-context-free.
To do this, let us assume that this language could be generated by some CFG in CNF. No matter how many live productions this grammar has, some word in this language is bigger than 2p.
Let us assume that the word w = a200b200a200 is big enough (if it's not, we've got a bag full of much bigger ones).
Now we show that any method of breaking w into five parts
w=uvxyz
will mean that
u v2 x y2 z
cannot be in {anbnan}. There are many ways of demonstrating this, but let us take the quickest.
Observation
All words in {anbnan} have exactly one occurrence of the substring ab no matter what n is.
Now if either the v-part or the y-part has the substring ab in it, then u v2 x y2 z will have more than one substring of ab, and so it cannot be in {{anbnan}.
Therefore, neither v nor y contains ab.
Observation
All words in {anbnan} have exactly one occurrence of the substring ba no matter what n is. Now if either the v part or the y part has the substring ba in it, then u v2 x y2 z has more than one such substring, which no word in {anbnan} does. Therefore, neither v nor y contains ba
The only possibility left is that v and y must be all a's, all b's, or Λ otherwise they would contain either ab or ba.
But if v and y are blocks of one letter, then u v2 x y2 z has increased one or two clumps of solid letters (more a's if v is a's, etc.).
However, there are three clumps of solid letters in the words in {anbnan}, and not all three of those clumps have been increased equally. This would destroy the form of the word.
For example, if
a200b200a200
= \( a^{200} b^{70} b^{40} b^{90} a^{82} a^3 a^{115} \)
then
u v2 x y2 z
= \( (a^{200} b^{70}) (b^{40})^2 (b^{90} a^{82}) (a^3)^2 (a^{115}) \)
= \( a^{200} b^{240} a^{203}\)
\( \neq a^nb^na^n \) for any nThe b's and the second clump of a's were increased, but not the first a's. The exponents are no longer the same.
We must emphasize that there is no possible decomposition of this w into uvxyz. It is not good enough to show that one partition into five parts does not work.
It should be understood that we have shown that any attempted partition into uvxyz must fail to have uvvxyyz in the language.
Therefore,' the Pumping Lemma cannot successfully be applied to the language {anbnan} at all. But the Pumping Lemma does apply to all context-free languages.
Therefore, {anbnan} is not a context-free language.
EXAMPLE
Let us take, just for the duration of this example, a language over the alphabet Σ = {a,b,c}. Consider the language:
{anbnan for n = 1 2 3 . . .} = { abc aabbcc aaabbbccc . . . }
We shall now prove that this language is non-context-free. Suppose it were context-free and suppose that the word w = a200b200a200
is large enough so that the Pumping Lemma applies to it. That means larger than 2P, where p is the number of live productions. We shall now show that no matter what choices are made for the five parts u, v, x, y, z:
u v2 x y2 z cannot be in the language.
Again we begin with some observations.
Observation
All words in anbnan have:
Only one substring ab
Only one substring bc
No substring ac
No substring ba
No substring ca
No substring cbno matter what n is. If v or y is not a solid block of one letter (or Λ), then u v2 x y2 z would have more of some of the two-letter substrings ab, ac, ba, bc, ca, cb than it is supposed to have.
On the other hand, if v and y are solid blocks of one letter (or Λ), then one or two of the letters a, b, c would be increased in the word uvvxyyz while the other letter (or letters) would not increase in quantity.
But all the words in anbnan have equal numbers of a's, b's, and c's. Therefore, the Pumping Lemma cannot apply to the language {anbnan}, which means that this language is non-context-free.
THEOREM
If w is a word in a regular language L and w is long enough, then w can be decomposed into three parts:
w = x y z such that all the words xyn z must also be in L.
THEOREM
If w is a word in a context-free language L and w is long enough, then w can be decomposed into five parts: w=uvxyz such that all the words u vn x yn x must also be in L
Symbol
There is another useful symbol that is employed in this subject. It is
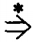 and it means "after some number of substitutions turns into." For example,
for the CFG:
and it means "after some number of substitutions turns into." For example,
for the CFG:
S → SSS | b
we could write: S
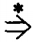 bbb
instead of:
S → SSS → SSb → Sbb → bbb
bbb
instead of:
S → SSS → SSb → Sbb → bbb
N is nullable if N
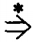 Λ
Λ
DEFINITION
In a particular CFG, a nonterminal N is called self-embedded if there are strings of terminals v and y not both null, such that N
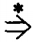 vNy
vNy This definition does not involve any tree diagrams, any geometric intuition, or any possibility of imprecision.
The Pumping Lemma can now be stated as follows.
Algebraic Form of the Pumping Lemma
If w is a word in a CFL and if w is long enough, [length(w) > 2p],then there
exists a nonterminal N and strings of terminals u, v, x, y, and z (where v and y are not both Λ) such that:
W = uvxyz
S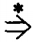 uNz
uNz
N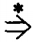 vNy
vNy
N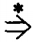 x
xand therefore
u vn x yn x must all be words in this language for any n.
The idea in the Algebraic Proof is
S
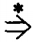 uNz
uNz
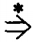 u (vNy) z
u (vNy) z
= (uv) N (yz)
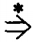 (uv) (vNy) (yz)
(uv) (vNy) (yz)
= (uv2) N (y2z)
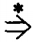 (uv2) (vNy) (y2z)
(uv2) (vNy) (y2z)
= uv3 N y3z
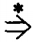 uvn N ynz
uvn N ynz
 uvn x ynz.
uvn x ynz.
THEOREM
Let L be a CFL in CNF with p live productions. Then any word w, in L with length > 2P can be broken into five parts:
W = uvxyz
such thatlength (vxy) ≤ 2P
length (x) > 0
length (v) + length (y) > 0
and such that all the words
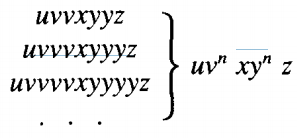
are all in the language L.
The discussion above has already proven this result.
EXAMPLE
Let us consider the language: L = {anbmanbm}
where n and m are integers 1, 2, 3 . . . and n does not necessarily equal m.
L = {abab aabaab abbabb aabbaabb aaabaaab . .. }
If we tried to prove that this language was non-context-free ; we could have reached :
u = Λ
v = first a's = ax
x = middle b's = by
y = second a's = ax
z = last b's = by
u vn x yn x
= Λ (ax)n by (ax)n byall of which are in L. Therefore we have no contradiction and the Pumping Lemma does apply to L.
Now let us try a second approach. If L did have a CFG that generates it, let that CFG in CNF have p live productions. Let us look at the word
a2p b2p a2p b2p
we know: length(vxy) < 2p
so v and y cannot be solid blocks of one letter separated by a clump of the other letter, since the separator letter clump is longer than the length of the whole substring vxy.
By the usual argument (counting substrings of "ab" and "ba"), we see that v and y must be one solid letter. But because of the length condition the letters must all come from the same clump. Any of the four clumps will do:
a2p b2p a2p b2p
However, this now means that some words not of the form anbmanbm
must also be in L. Therefore, L is non-context-free.