Computer programming languages are context-free. (We must be careful here to say that the languages in which the words are computer language instructions are context-free.

The languages in which the words are computer language programs are mostly not.) This makes CFG's of fundamental importance in the design of compilers.

Let us begin with the definition of what constitutes a valid storage location identifier in a higher-level language such as ADA, BASIC, COBOL ...

These user-defined names are often called variables. In some languages their length is limited to a maximum of six characters, where the first must be a letter and each character thereafter is either a letter or a digit. We can summarize this by the CFG:

identifier → letter (letter + digit + Λ)⁵
letter → A | B | C | . . | Z
digit → 0 | 1 | 2 | 3 ... |

Notice that we have used a regular expression for the right side of the first production instead of writing out all the possibilities:

identifier → letter | letter letter |
letter digit | letter letter letter |
letter letter digit | letter digit digit |

There are 63 different strings of nonterminals represented by letter (letter + digit + Λ)⁵

and the use of this shorthand notation is more understandable than writing out the whole list.

The first part of the process of compilation is the scanner.

This program reads through the original source program and replaces all the user-defined identifier names which have personal significance to the programmer, such as DATE, SALARY, RATE, NAME, MOTHER ..... with more manageable computer names that will help the machine move this information in and out of the registers as it is being processed.

The scanner is also called a lexical analyzer because its job is to build a lexicon (which is from Greek what "dictionary" is from Latin).

A scanner must be able to make some sophisticated decisions such as recognizing that DO33I is an identifier in the assignment statement
DO33I = 1100
while DO33I is part of a loop instruction in the statement
DO33I = 1,100
(or in some languages DO33I = 1TO100).

Other character strings, such as IF, ELSE, END, .... have to be recognized as reserved words even though they also fit the definition of identifier.

All this aside, most of what a scanner does can be performed by an FA, and scanners are usually written with this model in mind.

Another task a compiler must perform is to "understand" what is meant by arithmetic expressions such as

A3J * S + (7 * (BIL + 4))

After the scanner replaces all numbers and variables with the identifier labels i₁, i₂, ... , this becomes:

i₁ * i₂ + (i₃ * (i₄ + i₅))

The grammars we presented earlier for AE (arithmetic expression) were ambiguous. This is not acceptable for programming since we want the computer to know and execute exactly what we mean by this formula. Two possible solutions were mentioned earlier.

Programmers find the first solution too cumbersome and unnatural. Fortunately, there are grammars (CFG's) that satisfy the second requirement.

The rules of production are:

S → E
E → T + E | T
T → F * T | F
F → (E) | i

Loosely speaking, E stands for an expression, T for a term in a sum, F for a factor in a product, and i for any identifier. The terminals clearly are

+ * () i

since these symbols occur on the right side of productions but never on the left side.

To generate the word i + i * i by left-most derivation we must proceed:

S ⇒ E
⇒ T + E
⇒ F + E
⇒ i + E
⇒ i + T
⇒ i + F * T
⇒ i + i * T
⇒ i + i * F
⇒ i + i * i

The syntax tree for this is

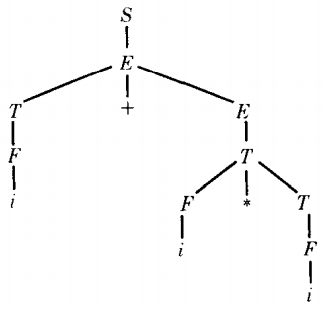
It is clear from this tree that the word represents the addition of an identifier with the product of two identifiers.

In other words, the multiplication will be performed before the addition, just as we intended it to be in accordance with conventional operator hierarchy.

Once the computer can discover a derivation for the formula, it can generate a machine-language program to accomplish the same task.

Given a word generated by a particular grammar, the task of finding its derivation is called parsing.

There are many different approaches to the problem of CFG parsing. We shall consider three of them.

The first two are general algorithms based on our study of derivation trees for CFG's. The third is specific to arithmetical expressions and makes use of the correspondence between CFG's and PDA's. The first algorithm is called top-down parsing.

We begin with a CFG and a target word. Starting with the symbol S, we try to find some sequence of productions that generates the target word. We do this by checking all possibilities for left-most derivations.

To organize this search we build a tree of all possibilities, which is like the whole language tree.

We grow each branch until it becomes clear that the branch can no longer present a viable possibility; that is, we discontinue growing a branch of the whole language tree as soon as it becomes clear that the target word will never appear on that branch, even generations later.

This could happen, for example, if the branch includes in its working string a terminal that does not appear anywhere in the target word or does not appear in the target word in a corresponding position.

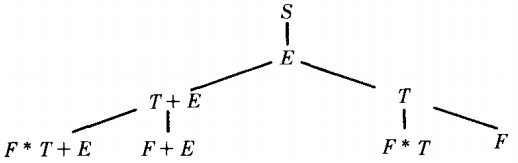
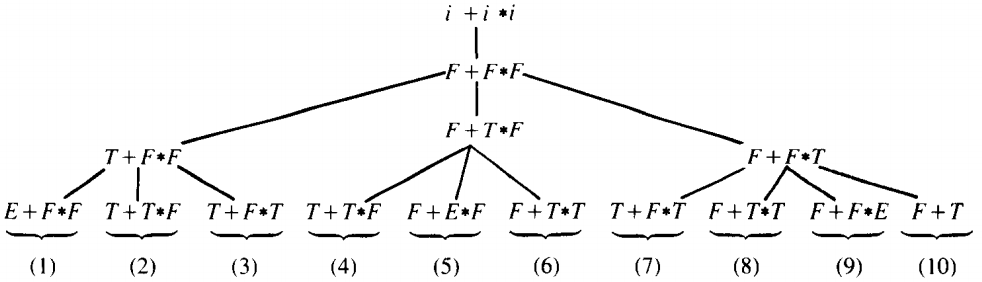
It is time to see an illustration. Let us consider the target word i+i*i in the language generated by the grammar PLUS-TIMES.

We begin with the start symbol S. At this point there is only one production we can possibly apply, S → E. From E there are two possible productions: E → T + E ; E → T

In each case, the left-most nonterminal is T and there are two productions possible for replacing this T.

The top-down left-most parsing tree begins as shown below:

In each of the bottom four cases the left-most nonterminal is F, which is the left side of two possible productions.

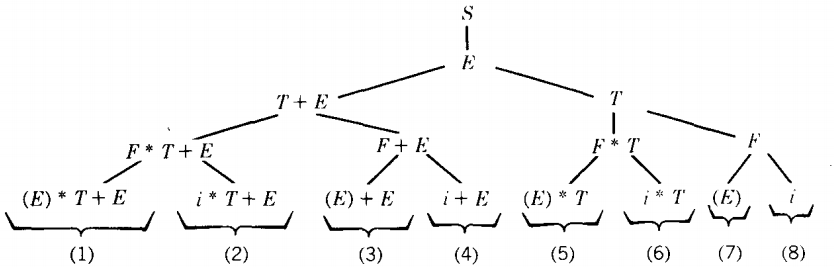
Of these, we can drop branches number 1, 3, 5, and 7 from further consideration because they have introduced the terminal character "(", which is not the first (or any) letter of our word. Once a terminal character appears in a working string, it never leaves.

Productions change the nonterminals into other things, but the terminals stay forever.

All four of those branches can produce only words with parentheses in them, not i + i * i. Branch 8 has ended its development naturally in a string of all terminals but it is not our target word, so we can discontinue the investigation of this branch too.

Our pruned tree looks like this:

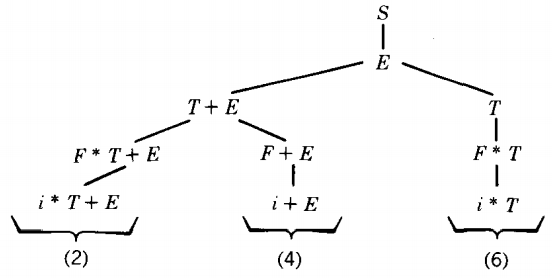
Since branches 7 and 8 both vanished, we dropped the line that produced them: T ⇒ F

All three branches have actually derived the first two terminal letters of the words that they can produce. Each of the three branches left starts with two terminals that can never change.

Branch 4 says the word starts with "i + ", which is correct, but branches 2 and 6 can now produce only words that start "i * ", which is not in agreement with our desired target word. The second letter of all words derived on branches 2 and 6 is *; the second letter of the target word is +. We must kill these branches before they multiply.

Deleting branch 6 prunes the tree up to the derivation E =' T, which has proved fruitless as none of its offshoots can produce our target word. Deleting branch 2 tells us that we can eliminate the left branch out of T + E.

With all of the pruning we have now done, we can conclude that any branch leading to i + i * i must begin S ⇒ E ⇒ T+E ⇒ F+E ⇒ i+E

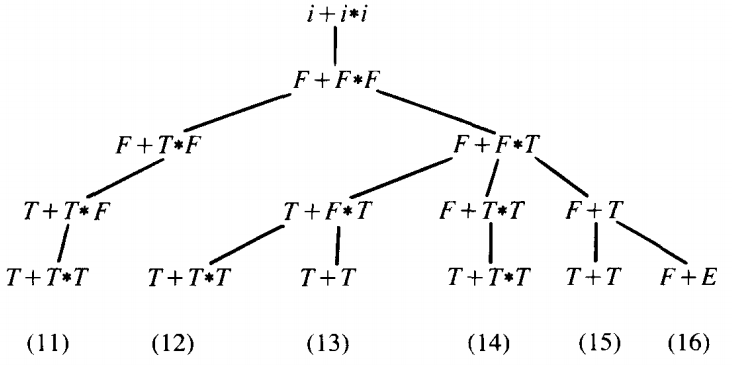
Let us continue this tree two more generations. We have drawn all derivation possibilities. Now it is time to examine the branches for pruning

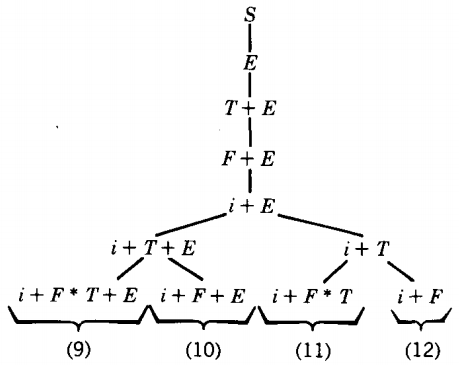
At this point we are now going to pull a new rule out of our hat. Since no production in any CFG can decrease the length of the working string of terminals and nonterminals on which it operates (each production replaces one symbol by one or more), once the length of a working string has passed five it can never produce a final word of length only five.

We can therefore delete branch 9 on this basis alone. No words that it generates can have as few as five letters.

Another observation we can make is that even though branch 10 is not too long and even though it begins with a correct string of terminals, it can still be eliminated because it has produced another + in the working string.

This is a terminal that all descendants on the branch will have to include. However, there is no second + in the word we are trying to derive. Therefore, we can eliminate branch 10, too.

This leaves us with only branches 11 and 12 which continue to grow.

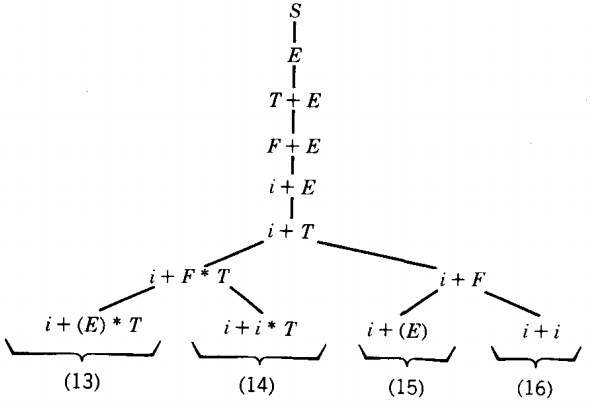
Now branches 13 and 15 have introduced the forbidden terminal "(", while branch 16 has terminated its growth at the wrong word. Only branch 14 deserves to live.

(At this point we draw the top half of the tree horizontally.) S ⇒ E ⇒ T + E ⇒ F + E ⇒ i + E ⇒ i + T ⇒ i + F * T

In this way we have discovered that the word i + i * i can be generated by this CFG and we have found the one left-most derivation which generates it

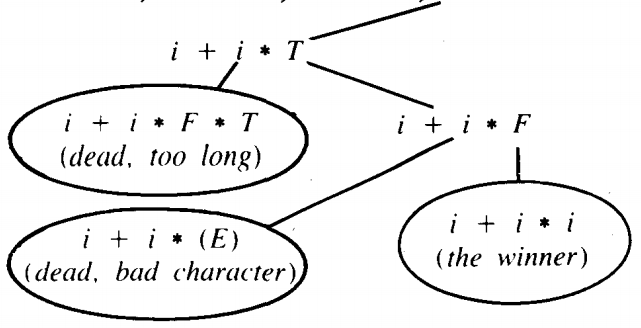
To recapitulate the algorithm:

Bad Substring: If a substring of solid terminals (one or more) has been introduced into a working string in a branch of the total-language tree, all words derived from it must also include that substring unaltered. Therefore, any substring that does not appear in the target word is cause for eliminating the branch.

Good Substrings But Too Many: The working string has more occurrences of the particular substring than the target word does. In a sense Rule 1 is a special case of this.

Good Substrings But Wrong Order: If the working string is YabXYbaXX but the target word is bbbbaab, then both substrings of terminals developed so far, ab and ba, are valid substrings of the target word but they do not occur in the same order in the working string as in the word. So the working string cannot develop into the target word.

Improper Outer-terminal Substring: Substrings of terminals developed at the beginning or end of the working string will always stay at the ends at which they first appear. They must be in perfect agreement with the target word or the branch must be eliminated.

. Excess Projected Length: If the working string is aXbbYYXa and if all the productions with a left side of X have right sides of six characters, then the shortest length of the ultimate words derived from this working string must have length at least 1 + 6 + 1 + 1 + 1 + 1 + 6 + 1 = 18. If the target word has fewer than 18 letters, kill this branch.

Wrong Target Word: If we have only terminals left but the string is not the target word, forget it. This is a special case of Rule 4, where the substring is the entire word. There may be even more rules depending on the exact nature of the grammar

Let us recall the CFG for the language EQUAL:

S → aB | bA
A → a | aS | bAA
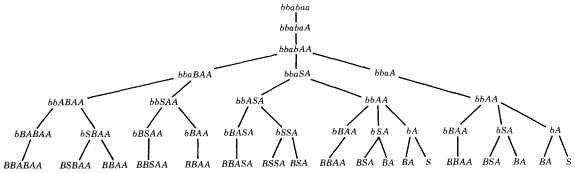
B → b | bS | aBB

The word bbabaa is in EQUAL. Let us determine a left-most derivation for this word by top-down parsing.

From the start symbol S the derivation tree can take one of two tracks

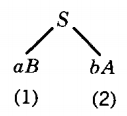
All words derived from branch 1 must begin with the letter a, but our target word does not. Therefore, by Rule 4, only branch 2 need be considered. The left-most nonterminal is A. There are three branches possible at this point.

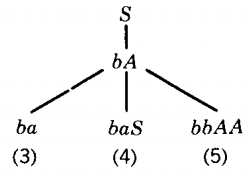
Branch 3 is a completed word but not our target word. Branch 4 will generate only words with an initial string of terminals ba, which is not the case with bbabaa.

Only branch 5 remains a possibility. The left-most nonterminal in the working string of branch 5 is the first A. Three productions apply to it:

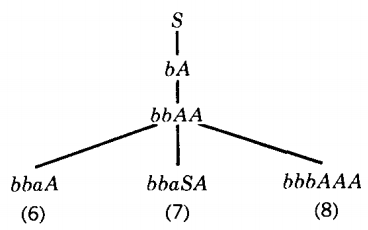
Branches 6 and 7 seem perfectly possible. Branch 8, however, has generated the terminal substring bbb, which all of its descendants must bear. This substring does not appear in our target word, so we can eliminate this branch from further consideration.

In branch 6 the left-most nonterminal is the A, in branch 7 it is the S.

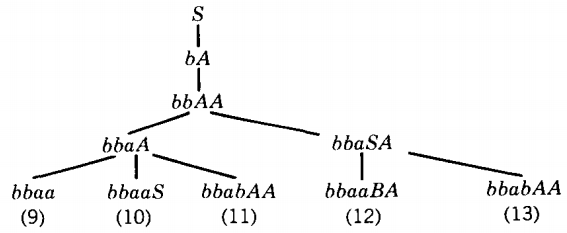
Branch 9 is a string of all terminals, but not the target word. Branch 10 has the initial substring bbaa; the target word does not. This detail also kills branch 12.

Branch 11 and branch 13 are identical. If we wanted all the leftmost derivations of this target word, we would keep both branches growing. Since we need only one derivation, we may just as well keep branch 13 and drop branch 11 (or vice versa); whatever words can be produced on one branch can be produced on the other.

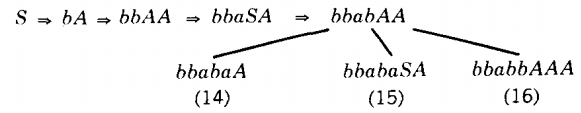
Only the working string in branch 14 is not longer than the target word. Branches 15 and 16 can never generate a six-letter word.

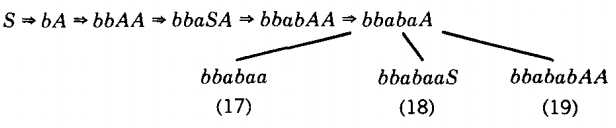
Branches 18 and 19 are too long, so it is a good thing that branch 17 is our word. This completes the derivation.

The next parsing algorithm we shall illustrate is the bottom-up parser. This time we do not ask what were the first few productions used in deriving the word, but what were the last few.

We work backward from the end to the front, the way sneaky people do when they try to solve a maze.

Let us again consider as our example the word i + i * i generated by the CFG PLUS-TIMES

If we are trying to reconstruct a left-most derivation, we might think that the last terminal to be derived was the last letter of the word. However, this is not always the case.

For example, in the grammar
S → Abb
A → a

the word abb is formed in two steps, but the final two b's were introduced in the first step of the derivation, not the last. So instead of trying to reconstruct specifically a left-most derivation, we have to search for any derivation of our target word. This makes the tree much larger. We begin at the bottom of the derivation tree, that is, with the target word itself, and step by step work our way back up the tree seeking to find when the working string was the one single S.

Let us reconsider the CFG PLUS-TIMES:
S → E
E → T + E | T
T → F * T | F
F → (E) | i

To perform a bottom-up search, we shall be reiterating the following step: Find all substrings of the present working string of terminals and nonterminals that are right halves of productions and substitute back to the nonterminal that could have produced them.

Three substrings of i + i * i are right halves of productions; namely, the three i's, anyone of which could have been produced by an F. The tree of possibilities begins as follows:

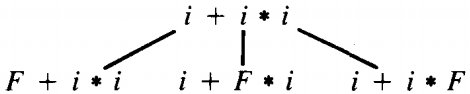
Even though we are going from the bottom of the derivation tree to the top S, we will still draw the tree of possibilities, as all our trees, from the top of the page downward.

We can save ourselves some work in this particular example by realizing that all of the i's come from the production F → i and the working string we should be trying to derive is F + F * F. Strictly speaking, this insight should not be allowed since it requires an idea that we did not include in the algorithm to begin with. But since it saves us a considerable amount of work, we succumb to the temptation and write in one step

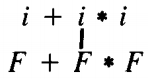
Not all the F's had to come from T → F. Some could have come from T → F * T, so we cannot use the same trick again.

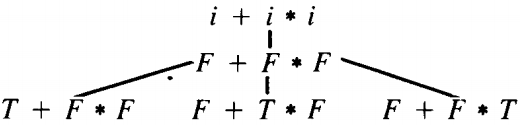
The first two branches contain substrings that could be the right halves of E → T and T → F. The third branch has the additional possibility of T → F * T. The tree continues

We never have to worry about the length of the intermediate strings in bottom-up parsing since they can never exceed the length of the target word.

At each stage they stay the same length or get shorter. Also, no bad terminals are ever introduced since no new terminals are ever introduced at all, only nonterminals. These are efficiencies that partially compensate for the inefficiency of not restricting ourselves to left-most derivations.

There is the possibility that a nonterminal is bad in certain contexts. For example, branch 1 now has an E as its left-most character. The only production that will ever absorb that E is S → E.

This would give us the nonterminal S, but S is not in the right half of any production. It is true that we want to end up with the S; that is the whole goal of the tree.

However, we shall want the entire working string to be that single S, not a longer working string with S as its first letter.

The rest of the expression in branch 1, " + F * F", is not just going to disappear. So branch 1 gets the ax. The E's in branch 5 and branch 9 are none too promising either, as we shall see in a moment. When we go backward, we no longer have the guarantee that the "inverse" grammar is unambiguous even though the CFG itself might be.

In fact, this backward tracing is probably not unique, since we are not restricting ourselves to finding a left-most derivation (even though we could with a little more thought; see Problem 10 below).

We should also find the trails of right-most derivations and whatnot. This is reflected in the occurrence of repeated expressions in the branches. In our example, branch 2 is now the same as branch 4, branch 3 is the same as branch 7, and branch 6 is the same as branch 8.

Since we are interested here in finding any one derivation, not all derivations, we can safely kill branches 2, 3, and 6 and still find a derivation-if one exists.

The tree grows ferociously, like a bush, very wide but not very tall. It would grow too unwieldy unless we made the following observation.

Observation

Let us again consider the grammar:
S → aB | bA
A → a | aS | bAA
B → b | bS | aBB

and again let us search for a derivation of a target word, this time through bottom-up parsing. Let us analyze the grammar before parsing anything. If we ever encounter the working string bAAaB

in a bottom-up parse in this grammar, we shall have to determine the working strings from which it might have been derived. We scan the string looking for any substrings of it that are the right sides of productions. In this case there are five of them: b bA bAA a aB

Notice how they may overlap. This working string could have been derived in five ways:

BAAaB ⇒ bAAaB (B → b)
SAaB ⇒ bAAaB (S → bA)
AaB ⇒ bAAaB (A → bAA)
bAAAB ⇒ bAAaB (A → a)
bAAS ⇒ bAAaB (S → aB)

Let us make some observations peculiar to this grammar.

1. All derivations in this grammar begin with either S → aB or S → bA, so the only working string that can ever begin with a nonterminal is the working string is S. For example the pseudo-working string AbbA cannot occur in a derivation.

2. Since the application of each rule of production creates one new terminal in the working string, in any derivation of a word of length 6 (or n), there are exactly 6 (or n) steps.

3. Since every rule of production is in the form Nonterminal → (one terminal) (string of 0, 1, or 2 Nonterminals) in a left-most derivation we take the first nonterminal from the string of nonterminals and replace it with terminals followed by nonterminals.

Therefore, all working strings will be of the form
terminal terminal. . . terminal Nonterminal Nonterminal . . . Nonterminal
= terminal* Nonterminal*
= (string of terminals) (string of Nonterminals)

If we are searching backward and have a working string before us, then the working strings it could have come from have all but one of the same terminals in front and a small change in nonterminals where the terminals and the nonterminals meet.

For example,
baabbababaBBABABBBAAAA
could have been left-most produced only from these three working strings.
baabbababABBABABBBAAAA,
baabbababSBABABBBAAAA,
baabbababBABABBBAAAA

We now use the bottom-up algorithm to find a left-most derivation for the target word bbabaa.

On the bottom row there are two S's. Therefore, there are two left-most derivations of this word in this grammar:

S ⇒ bA ⇒ bbAA ⇒ bbaSA ⇒ bbabAA ⇒ bbabaA ⇒ bbabaa
S ⇒ bA ⇒ bbAA ⇒ bbaA ⇒ bbabAA ⇒ bbabaA ⇒ bbabaa

Notice that all the other branches in this tree die simultaneously, since they now contain no terminals.

This applies not only to arithmetic expressions but also to many other programming language instructions as well.

We shall assume that we are now using postfix notation, where the two operands immediately precede the operator:

A + B becomes A B +
(A + B)*C becomes AB + C*
A * (B + C * D) becomes A B C D * + *

An algorithm for converting standard infix notation into postfix notation was given before.

Once an expression is in postfix, we can evaluate it without finding its derivation from a CFG, although we originally made use of its parsing tree to convert the infix into postfix in the first place.

We are assuming here that our expressions involve only numerical values for the identifiers (i's) and only the operations + and *, as in the language PLUS-TIMES.

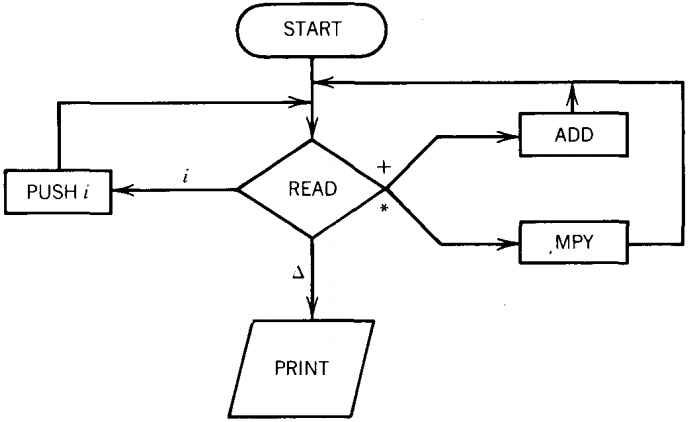
We can evaluate these postfix expressions by a new machine similar to a PDA. Such a machine requires three new states.

The machine to evaluate postfix expressions can now be built as below, where the expression to be evaluated has been put on the INPUT TAPE in the usual fashion--one character per cell starting in the first cell.

Let us trace the action of this machine on the input string:

7 5 + 2 4 + * 6 +
which is postfix for
(7 + 5) * (2 + 4) + 6 = 78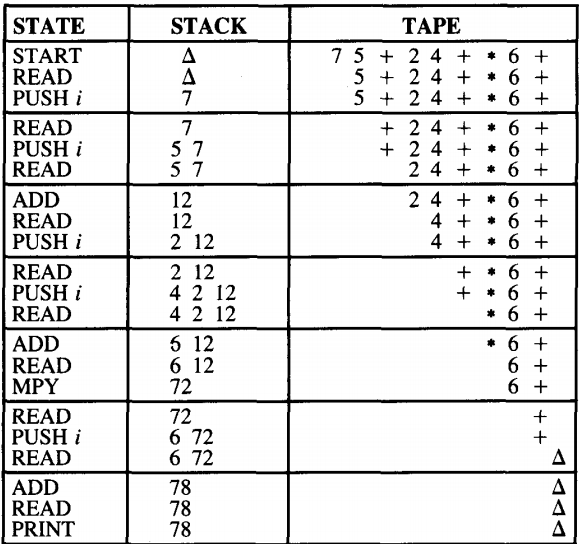

Notice that when we arrive at PRINT the stack has only one element in it.

What we have been using here is a PDA with arithmetic and output capabilities. Just as we expanded FA's to Mealy and Moore machines, we can expand PDA's to what are called pushdown transducers.

These are very important but belong to the study of the Theory of Compilers.

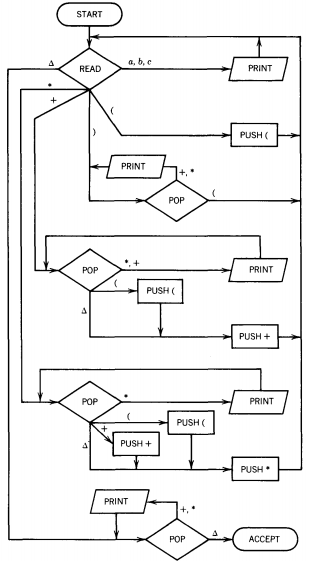
The task of converting infix arithmetic expressions (normal ones) into postfix can also be accomplished by a pushdown transducer as an alternative to depending on a dotted line circling a parsing tree.

This time all we require is a PDA with an additional PRINT instruction.

The input string will be read off of the TAPE character by character.

If the character is a number (or, in our example, the letters a, b, c), it is immediately printed out, since the operands in postfix occur in the same order as in the infix equivalent.

The operators, however, + and * in our example, must wait to be printed until after the second operand they govern has been printed. The place where the operators wait is, of course, the STACK. If we read a + b, we print a, push +, print b, pop +, print +.

The output states we need are

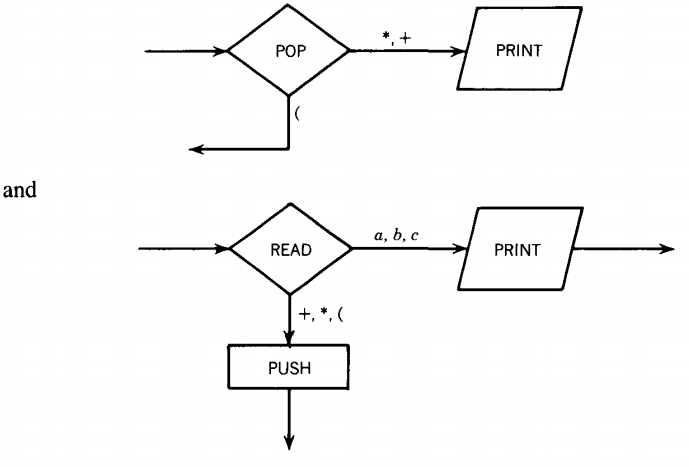
"POP-PRINT" prints whatever it has just popped, and the READ-PRINT prints the character just read.

The READ-PUSH pushes whatever character "+" or "*" or "(" labels the edge leading into it. These are all the machine parts we need.

One more comment should be made about when an operator is ready to be popped. The second operand is recognized by encountering (1) a right parenthesis, (2) another operator having equal or lower precedence, or (3) the end of the input string.

When a right parenthesis is encountered, it means that the infix expression is complete back up to the last left parenthesis.

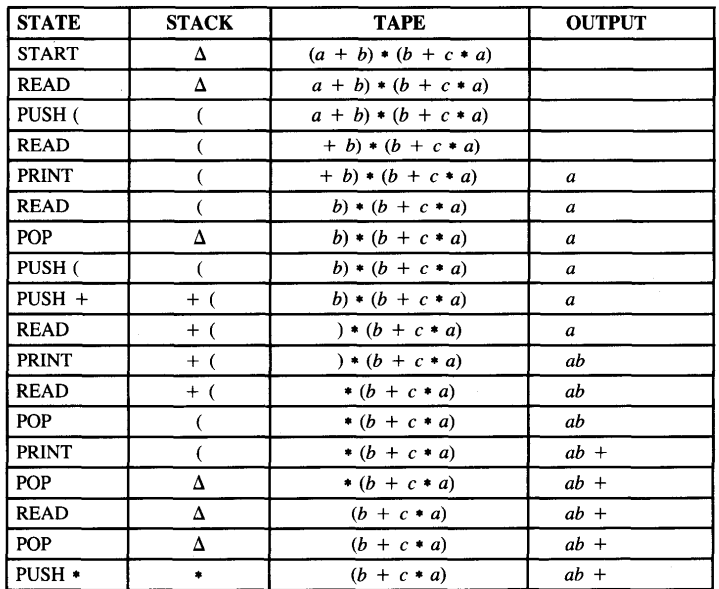
For example, consider the expression
a * (b + c) + b + c
The pushdown transducer will do the following:
1. Read a, print a
2. Read *, push *
3. Read (, push
4. Read b, print b
5. Read +, push +
6. Read c, print c
7. Read ), pop +, print +
8. Pop(
9. Read +, we cannot push + on top of * because of operator precedence, so pop *, print *, push +
10. Read b, print b
11. Read +, we cannot push + on top of +, so print +
12. Read c, print c
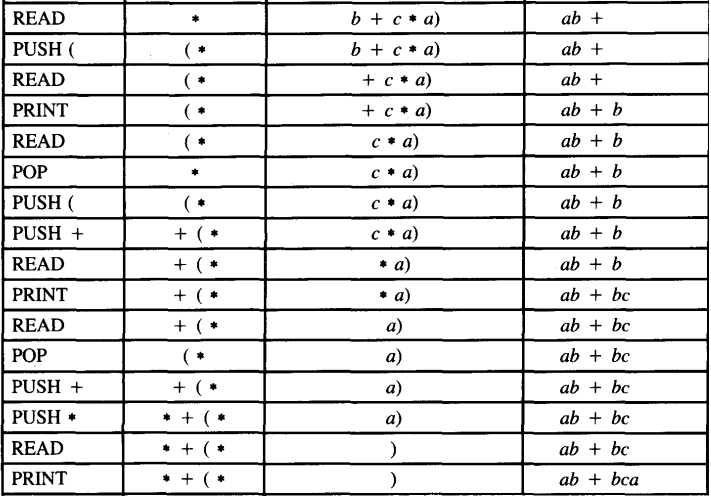
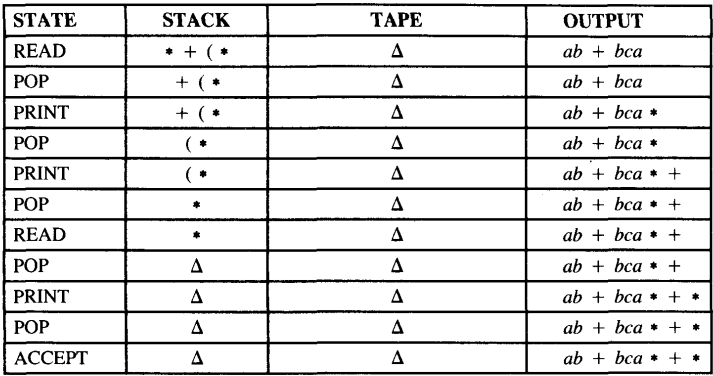
13. Read △, pop +, print +.

The resulting output sequence is
abc + * b + c +
which indeed is the correct postfix equivalent of the input.

Notice that operator precedence is "built into" this machine. Generalizations of this machine can handle any arithmetic expressions including -, /, and **

Notice that the printing takes place on the right end of the output sequence.

One trivial observation is that this machine will never print any parentheses.

No parentheses are needed to understand postfix or prefix notation.

Another is that every operator and operand in the original expression will be printed out.

The major observation is that if the output of this transducer is then fed into the previous transducer, the original infix arithmetic expression will be evaluated correctly.

In this way we can give a PDA an expression in normal arithmetic notation, and the PDA will evaluate it.