DECIDABILITY



  • There are no algorithms to resolve any of these questions. No algorithms have been found because no such algorithms exist-anywhere--ever.


    • 1. How can we tell whether or not two different CFG's define the same language?


    • 2. Given a particular CFG, how can we tell whether or not it is ambiguous?


    • 3. Given a CFG, how can we tell whether or not it has an equivalent PDA that is deterministic?


    • 4. Given a CFG that is ambiguous, how can we tell whether or not there is a different CFG that generates the same language but is not ambiguous?


    • 5. How can we tell whether or not the complement of a given context-free language is also context-free?


    • 6. How can we tell whether or not the intersection of two context-free languages is also context-free?


    • 7. Given two context-free grammars, how can we tell whether or not they have a word in common?


    • 8. Given a CFG, how can we tell whether or not there are any words that it does not generate? (Is its language all (a + b)* or not?)


  • There are, however, some other fundamental questions about CFG's that we can answer.


    • 1. Given a CFG, can we tell whether or not it generates any words at all? This is the question of emptiness.


    • 2. Given a CFG, can we tell whether or not the language it generates is finite or infinite? This is the question of finiteness.


    • 3. Given a CFG and a particular string of letters w, can we tell whether or not w can be generated by the CFG? This is the question of membership.




THEOREM



  • Given any CFG, there is an algorithm to determine whether or not it can generate any words.


  • PROOF


    1. The proof will be by constructive example. We show there exists such an algorithm by presenting one.


    2. We showed that every CFG that does not generate Λ can be written without Λ-productions.


    3. In that proof we showed how to decide which nonterminals are nullable.


    4. The word Λ is a word generated by the CFG if and only if S is nullable. We already know how to decide whether the start symbol S is nullable: S rightarrow Λ?


    5. Therefore, the problem of determining whether Λ is a word in the language of any CFG has already been solved.


    6. Let us assume now that Λ is not a word generated by the CFG. In that case, we can convert the CFG to CNF preserving the entire language. If there is a production of the form S → t


    7. where t is a terminal, then t is a word in the language. If there are no such productions we then propose the following algorithm.


    8. Step 1 : For each nonterminal N that has some productions of the form N → t ; where t is a terminal or string of terminals, we choose one of these productions and throw out all other productions for which N is on the left side. We then replace N by t in all the productions in which N is on the right side, thus eliminating the nonterminal N altogether. We may have changed the grammar so that it no longer accepts the same language. It may no longer be in CNF. That is fine with us. Every word that can be generated from the new grammar could have been generated by the old CFG. If the old CFG generated any words, then the new one does also.


    9. Step 2 Repeat Step 1 until either it eliminates S or it eliminates no new nonterminals. If S has been eliminated, then the CFG produces some words, if not then it does not. The algorithm is clearly finite, since it cannot run Step 1 more times than there are nonterminals in the original CNF version. The string of nonterminals that will eventually replace S is a word that could have been derived from S if we retraced in reverse the exact sequence of steps that lead from the terminals to S. If Step 2 makes us stop while we still have not replaced S, then we can show that no words are generated by this CFG. If there were any words in the language we could retrace the tree from any word and follow the path back to S.




Example



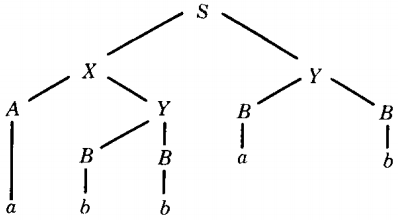
  • For example, if we have the derivation tree:


    • rightarrow

  • then we can trace backward as follows (the relevant productions can be read from the tree): B → b


  • must be a production, so replace all B's with b's: Y → BB


  • is a production, so replace Y with bb: A → a


  • is a production, so replace A with a: X → AY


  • is a production, so replace X with abb. S → XY


  • is a production, so replace S with abbbb. Even if the grammar included some other production; for example B → d (where d is some other terminal)


  • we could still retrace the derivation from abbbb to S, but we could just as well end up replacing S by adddd - if we chose to begin the backup by replacing all B's by d instead of by b.


  • The important fact is that some sequence of backward replacements will reach back to S if there is any word in the language. The proposed algorithm is therefore a decision procedure.




EXAMPLE



  • Consider this CFG:
    S → XY
    X → AX
    X → AA
    A → a
    Y → BY
    Y → BB
    B → b


  • Step 1 Replace all A's by a and all B's by b. This gives:
    S → XY
    X → aX
    X → aa
    Y → bY
    Y → bb


  • Step 1 Replace all X's by aa and all Y's by bb S → aabb


  • Step 1 Replace all S's by aabb.


  • Step 2 Terminate Step 1 and discover that S has been eliminated. Therefore, the CFG produces at least one word.




EXAMPLE



  • Consider this CFG:
    S → XY
    X → AX
    A → a
    Y → BY
    Y → BB
    B → b


  • Step 1 Replace all A's by a and all B's by b. This gives:
    S → XY
    X → aX
    Y → bY
    Y → bb


  • Step 1 Replace all Y's by bb. This gives:
    S → Xbb
    X → aX


  • Step 2 Terminate Step 1 and discover that S is still there. This CFG generates no words.




EXAMPLE



  • Consider this CFG:
    S → XY
    X → ZX
    Z → a
    X → AX
    X → ZZ
    Y → BB
    B → b
    A → XA


  • Step 1 Replace all Z's by a and all B's by b. This gives:
    S → XY
    X → aX
    X → AX
    X → aa
    Y → bb
    A → XA


  • Step 1 Replace all X's by aa and all Y's by bb. This gives:
    S → aabb
    A → aaA


  • Step 1 Replace all S's with aabb. This gives:
    A → aaA


  • Step 2 Terminate Step 1 and discover that S has been eliminated. This CFG generates at least one word, even though when we terminated Step 1 there were still some productions left. We notice that the nonterminal A can never be used in the derivation of a word.




THEOREM



  • There is an algorithm to decide whether or not a given nonterminal X in a given CFG is ever used in the generation of words.


  • PROOF


    1. Following the algorithm of the previous theorem until no new nonterminals can be eliminated will tell us which nonterminals can produce strings of ter- minals. Clearly, all nonterminals left cannot produce strings of terminals and all those replaced can.


    2. However, it is not enough to know that a particular nonterminal (call it X) can produce a string of terminals. We must also determine whether it can be reached from S in the middle of a derivation.


    3. In other words, there are two things that could be wrong with X.


    4. 1. X produces strings of terminals but cannot be reached from S. For example in
      S → Ya | Yb
      Y → ab
      X → aY | b


    5. 2. X can be reached from S but only in working strings that involve useless nonterminals that prevent word derivations. For example in
      S → Ya | Yb | a
      Y → XZ
      X → ab
      Z → Y


    6. Here Z is useless in the production of words, so Y is useless in the production of words, so X is useless in the production of words.


    7. The algorithm that will resolve these issues is of the blue paint variety.


      1. Step 1 Use the algorithm to find out which nonterminals cannot produce strings of terminals. Call these useless.


      2. Step 2 Purify the grammar by eliminating all productions involving the useless nonterminals. If X has been eliminated, we are done. If not, proceed.


      3. Step 3 Paint all X's blue.


      4. Step 4 If any nonterminal is the left side of a production with anything blue on the right, paint it blue, and paint all occurrences of it throughout the grammar blue, too.


      5. Step 5 The key to this approach is that all the remaining productions are guaranteed to terminate. This means that any blue on the right gives us blue on the left. Repeat Step 4 until nothing new is painted blue.


      6. Step 6 If S is blue, X is a useful member of the CFG, since there are words with derivations that involve X-productions. If not, X is not useful. Obviously, this algorithm is finite, since the only repeated part is Step 4 and that can be repeated only as many times as there are nonterminals in the grammar.


    8. It is also clear that if X is used in the production of some word, then S will be painted blue, since if we have
      S ⇒ ... ⇒ (blah) X (blah) ⇒ ... ⇒ word


    9. then the nonterminal that put X into the derivation in the first place will be blue, and the nonterminal that put that one in will be blue,- and the nonterminal from which that came will be blue . . . up to S.


    10. Now let us say that S is blue. Let us say that it caught the blue through this sequence: X made A blue and A made B blue and B made C blue . . . up to S. The production in which X made A blue looked like this:
      A → (blah) X (blah)


    11. Now the two (blah)'s might not be strings of terminals, but it must be true that any nonterminals in the (blah)'s can be turned into strings of terminals because they survived Step 2. So we know that there is a derivation from A to a string made up of X with terminals


    12. A rightarrow (string of terminals) X (string of terminals)


    13. We also know that there is a production of the form
      B ⇒ (blah) A (blah)
      that can likewise be turned into


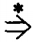    14. B rightarrow (string of terminals) A (string of terminals)
      rightarrow (string of terminals) X (string of terminals)


    15. We now back all the way up to S and realize that there is a derivation


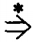    16. S rightarrow (string of terminals) X (string of terminals)
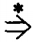      rightarrow (word)


    17. Therefore, this algorithm is exactly the decision procedure we need to decide if X is actually ever used in the production of a word in this CFG.