TURING MACHINES
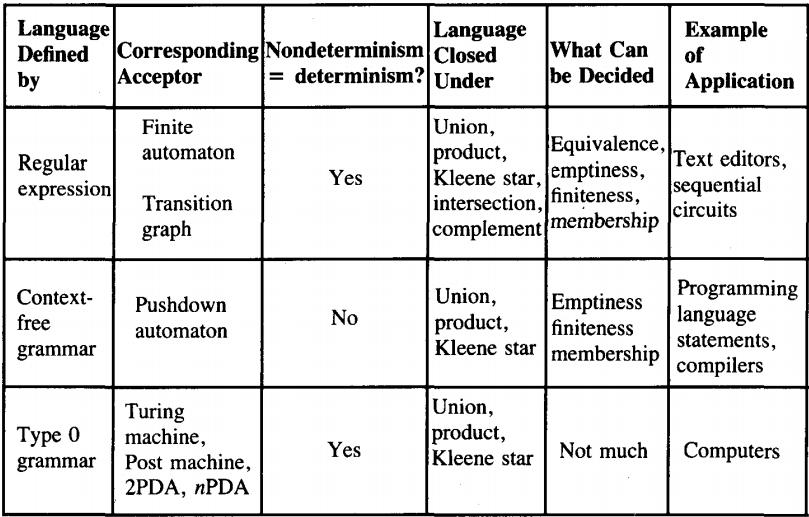
We see from the lower right entry in the table that we shall soon provide a mathematical model for the entire family of modem-day computers.
This model will enable us not only to study some theoretical limitations on the tasks that computers can perform, it will also be a model that we can use to show that certain operations can be done by computer.
This new model will turn out to be surprisingly like the models we have been studying so far.
Another interesting observation we can make about the bottom row of the table is that we take a very pessimistic view of our ability to decide the important questions about this mathematical model (which as we see is called a Turing machine).
We shall prove that we cannot even decide if a given word is accepted by a given Turing machine. This situation is unthinkable for FA's or PDA's, but now it is one of the unanticipated facts of life.
There is a definite progression in the rows of this table. All regular languages are context-free languages, and we shall see that all context-free languages are Turing machine languages. Historically, the order of invention of these ideas is:
Regular languages and FA's were developed by Kleene, Mealy, Moore, Rabin, and Scott in the 1950s.
CFG's and PDA's were developed later, by Chomsky, Oettinger, Schutzenberger, and Evey, mostly in the 1960s.
Turing machines and their theory were developed by Alan Mathison Turing and Emil Post in the 1930s and 1940s.
It is less surprising that these dates are out of order than that Turing's work predated the invention of the computer itself.
It was directly from the ideas in his work on mathematical models that the first computers were built.
Since Turing machines will be our ultimate model for computers, they will necessarily have output capabilities. Output is very important, so important that a program with no output statements might seem totally useless because it would never convey to humans the result of its calculations.
We may have heard it said that the one statement every program must have is an output statement. This is not exactly true. Consider the following program (written in no particular language):
1. READ X
2. IF X = 1 THEN END
3. IF X = 2 THEN DIVIDE X BY 0
4. IF X > 2 THEN GOTO STATEMENT 4Let us assume that the input is a positive integer. If the program terminates naturally, then we know X was 1. If it terminates by creating overflow or was interrupted by some error message warning of illegal calculation (crashes), then we know that X was 2.
If we find that our program was terminated because it exceeded our alloted time on the computer, then we know X was greater than 2. We shall see in a moment that the same trichotomy applies to Turing machines.
DEFINITION
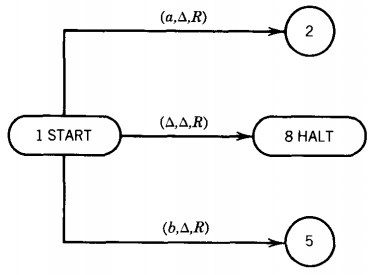
A Turing machine, denoted TM, is a collection of six things:
An alphabet Σ of input letters, which for clarity's sake does not contain the blank symbol △.
A TAPE divided into a sequence of numbered cells each containing one character or a blank. The input word is presented to the machine one letter per cell beginning in the left-most cell, called cell i. The rest of the TAPE is initially filled with blanks, △'s.

A TAPE HEAD that can in one step read the contents of a cell on the TAPE, replace it with some other character, and reposition itself to the next cell to the right or to the left of the one it has just read. At the start of the processing, the TAPE HEAD always begins by reading the input in cell i. The TAPE HEAD can never move left from cell i. If it is given orders to do so, the machine crashes.
An alphabet, Γ, of characters that can be printed on the TAPE by the TAPE HEAD. This can include Σ. Even though we allow the TAPE HEAD to print a △ we call this erasing and do not include the blank as a letter in the alphabet Γ.
A finite set of states including exactly one START state from which we begin execution (and which we may reenter during execution) and some (maybe none) HALT states that cause execution to terminate when we enter them. The other states have no functions, only names:
q1, q2, q3, .-. . or 1, 2, 3, ...
A program, which is a set of rules that tell us, on the basis of the letter the TAPE HEAD has just read, how to change states, what to print and where to move the TAPE HEAD. We depict the program as a collection of directed edges connecting the states. Each edge is labeled with a triplet of information: (letter, letter, direction)
The first letter (either △ or from Σ or Γ) is the character the TAPE HEAD reads from the cell to which it is pointing. The second letter (also △ or from Γ) is what the TAPE HEAD prints in the cell before it leaves. The third component, the direction, tells the TAPE HEAD whether to move one cell to the right, R, or one cell to the left, L.
No stipulation is made as to whether every state has an edge leading from it for every possible letter on the TAPE. If we are in a state and read a letter that offers no choice of path to another state, we crash; that means we terminate execution unsuccessfully. To terminate execution of a certain input successfully we must be led to a HALT state. The word on the input TAPE is then said to be accepted by the TM.
A crash also occurs when we are in the first cell on the TAPE and try to move the TAPE HEAD left.
By definition, all Turing machines are deterministic. This means that there is no state q that has two or more edges leaving it labeled with the same first letter.
For example,
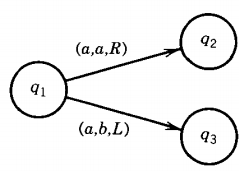
is not allowed.
EXAMPLE
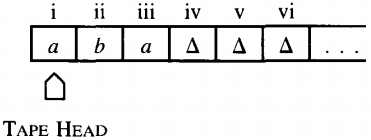
The following is the TAPE from a Turing machine about to run on the input aba
The program for this TM is given as a directed graph with labeled edges as shown below
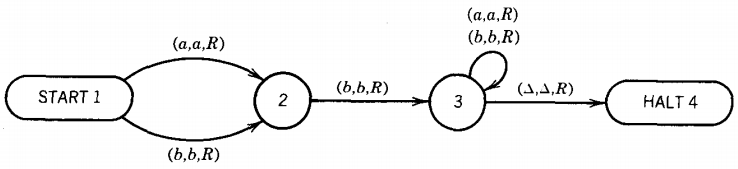
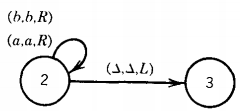
Notice that the loop at state 3 has two labels. The edges from state 1 to state 2 could have been drawn as one edge with two labels. We start, as always, with the TAPE HEAD reading cell i and the program in the start state, which is here labeled state 1. We depict this as
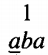
The number on top is the number of the state we are in. Below that is the current meaningful contents of the string on the TAPE up to the beginning of the infinite run of blanks.
It is possible that there may be a △ inside this string. We underline the character in the cell that is about to be read. At this point in our example, the TAPE HEAD reads the letter a and we follow the edge (a,a,R) to state 2.
The instructions of this edge to the TAPE HEAD are "read an a, print an a, move right." The TAPE now looks like this:
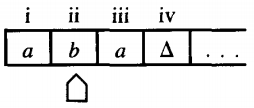
Notice that we have stopped writing the words "TAPE HEAD" under the indicator under the TAPE. It is still the TAPE HEAD nonetheless. We can record the execution process by writing:
At this point we are in state 2. Since we are reading the b in cell ii, we must take the ride to state 3 on the edge labeled (b,b,R). The TAPE HEAD replaces the b with a b and moves right one cell. The idea of replacing a letter with itself may seem silly, but it unifies the structure of Turing machines.
We could instead have constructed a machine that uses two different types of instructions: either print or move, not both at once. Our system allows us to formulate two possible meanings in a single type of instruction.
(a, a, R) means move, but do not change the TAPE cell (a, b, R) means move and change the TAPE cell This system does not give us a one-step way of changing the contents of the TAPE cell without moving the TAPE HEAD, but we shall see that this too can be done by our TM's.
Back to our machine. We are now up to
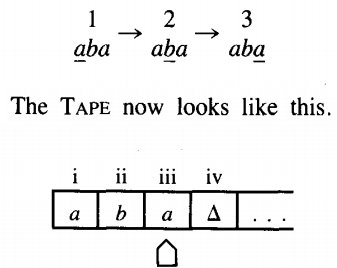
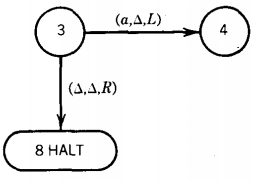
We are in state 3 reading an a, so we loop. That means we stay in state 3 but we move the TAPE HEAD to cell iv.
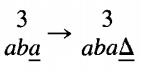
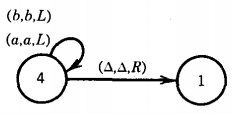
This is one of those times when we must indicate a △ as part of the meaningful contents of the TAPE. We are now in state 3 reading a △, so we move to state 4
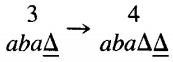
The input string aba has been accepted by this TM. This particular machine did not change any of the letters on the TAPE, SO at the end of the run the TAPE still reads abaA . . . . This is not a requirement for the acceptance of a string, just a phenomenon that happened this time.
In summary, the whole execution can be depicted by the following execution chain, also called a process chain, or a trace of execution, or simply a trace:
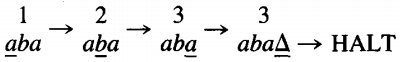
This is a new use for the arrow. It is neither a production nor a derivation. Let us consider which input strings are accepted by this TM. Any first letter, a or b, will lead us to state 2.
From state 2 to state 3 we require that we read the letter b. Once in state 3 we stay there as the TAPE HEAD moves right and right again, moving perhaps many cells until it encounters a A. Then we get to the HALT state and accept the word. Any word that reaches state 3 will eventually be accepted.
If the second letter is an a, then we crash at state 2. This is because there is no edge coming from state 2 with directions for what happens when the TAPE HEAD reads an a.
The language of words accepted by this machine is: All words over the alphabet {a,b} in which the second letter is a b.
This is a regular language because it can also be defined by the regular expression: (a + b)b(a + b)*
This TM is also reminiscent of FA's', making only one pass over the input string, moving its TAPE HEAD always to the right, and never changing a letter it has read.
EXAMPLE
Consider the following TM.
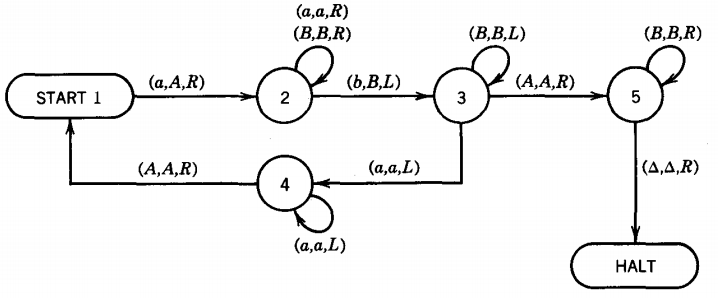
We have only drawn the program part of the TM, since initial appearance of the TAPE depends on the input word. This is a more complicated example of a TM. We analyze it by first explaining what it does and then recognizing how it does it.
The language this TM accepts is {anbn}.
By examining the program we can see that the TAPE HEAD may print any of the letters a, A or B, or a △ , and it may read any of the letters a, b, A or B or a blank. Technically, the input alphabet is Σ = {a, b} and the output alphabet is Γ = {a, A, B}, since △ is the symbol for a blank or empty cell and is not a legal character in an alphabet.
Let us describe the algorithm, informally in English , before looking at the directed graph that is the program. Let us assume that we start with a word of the language {anbn} on the TAPE.
We begin by taking the a in the first cell and changing it to the character A . (If the first cell does not contain an a, the program should crash. We can arrange this by having only one edge leading from START and labeling it to read an a.) The conversion from a to A means that this a has been counted.
We now want to find the b in the word that pairs off with this a. So we keep moving the TAPE HEAD to the right, without changing anything it passes over, until it reaches the first b. When we reach this b, we change it into the character B, which again means that it too has been counted.
Now we move the TAPE HEAD back down to the left until it reaches the first uncounted a. The first time we make our descent down the TAPE this will be the a in cell ii.
How do we know when we get to the first uncounted a? We cannot tell the TAPE HEAD to "find cell ii ." This instruction is not in its repertoire. We can, however, tell the TAPE HEAD to keep moving to the left until it gets to the character A.
When it hits the A we bounce one cell to the right and there we are. In doing this the TAPE HEAD passed through cell ii on its way down the TAPE. However, when we were first there we did not recognize it as our destination.
Only when we bounce off of our marker , the first A encountered, do we realize where we are. Half the trick in programming TM's is to know where the TAPE HEAD is by bouncing off of landmarks.
When we have located this left-most uncounted a we convert it into an A and begin marching up the TAPE looking for the corresponding b. This means that we skip over some a's and over the symbol B, which we previously wrote, leaving them unchanged, until we get to the first uncounted b.
Once we have located it , we have found our second pair of a and b. We count this second b by converting it into a B, and we march back down the TAPE looking for our next uncounted a. This will be in cell iii.
Again, we cannot tell the TAPE HEAD , "find cell iii." We must program it to find the intended cell. The same instructions as given last time work again. Back down to the first A we meet and then up one cell.
As we march down we walk through a B and some a's until we first reach the character A . This will be the second A, the one in cell ii. We bounce off this to the right, into cell iii, and find an a. This we convert to A and move up the TAPE to find its corresponding b.
This time marching up the TAPE we again skip over a's and B's until we find the first b. We convert this to B and march back down looking for the first unconverted a. We repeat the pairing process over and over.
What happens when we have paired off all the a's and b's? After we have converted our last b into a B and we move left looking for the next a we find that after marching left back through the last of the B's we encounter an A. We recognize that this means we are out of little a's in the initial field of a's at the beginning of the word.
We are about ready to accept the word , but we want to make sure that there are no more b's that have not been paired off with a's, or any extraneous a's at the end. Therefore we move back up through the field of B's to be sure that they are followed by a blank, otherwise the word initially may have been aaabbbb or aaabbba.
When we know that we have only A's and B's on the TAPE, in equal number, we can accept the input string.
The following is a picture of the contents of the TAPE at each step in the processing of the string aaabbb. Remember, in a trace the TAPE HEAD is indicated by the underlining of the letter it is about to read.

Based on this algorithm we can define a set of states that have the following meanings: State I This is the start state, but it is also the state we are in whenever we are about to read the lowest unpaired a. In a PDA we can never return to the START state, but in a TM we can. The edges leaving from here must convert this a to the character A and move the TAPE HEAD right and enter state 2.
State 2 This is the state we are in when we have just converted an a to an A and we are looking for the matching b. We begin moving up the TAPE. If we read another a, we leave it alone and continue to march up the TAPE, moving the TAPE HEAD always to the right.
If we read a B , we also leave it alone and continue to move the TAPE HEAD right. We cannot read an A while in this state. In this algorithm all the A's remain to the left of the TAPE HEAD once they are printed. If we read △ while we are searching for the b we are in trouble because we have not paired off our a. So we crash.
The first b we read, if we are lucky enough to find one, is the end of the search in this state . We convert it to B, move the TAPE HEAD left and enter state 3.
State 3 This is the state we are in when we have just converted a b to B. We should now march left down the TAPE looking for the field of unpaired a's. If we read a B, we leave it alone and keep moving left. If and when we read an a, we have done our job. We must then go to state 4, which will try to find the left-most unpaired a.
If we encounter the character b while moving to the left , something has gone very wrong and we should crash. If, however, we encounter the character A before we hit an a, we know that used up the pool of unpaired a's at the beginning of the input string and we may be ready to terminate execution. Therefore, we leave the A alone and reverse directions to the right and move into state 5.
State 4 We get here when state 3 has located the right-most end of the field of unpaired a's. The TAPE and TAPE HEAD situation looks like this:

In this state we must move left through a block of solid a's (we crash if we encounter a b, a B, or a △) until we find an A. When we do, we bounce off it to the right, which lands us at the left-most uncounted a. This means that we should next be in state 1 again.
State 5 When we get here it must be because state 3 found that there were no unpaired a's left and it bounced us off the right-most A. We are now reading the left-most B as in the picture below:

It is now our job to be sure that there are no more a's or b's left in this word. We want to scan through solid B's until we hit the first blank. Since the program never printed any blanks, this will indicate the end of the input string. If there are no more surprises before the △, we then accept the word by going to the state HALT. Otherwise we crash. For example, aabba would become AABBa and then crash because while searching for the △ we find an a.
This explains the TM program that we began with. It corresponds to the description above state for state and edge for edge. Let us trace the processing of the input string aabb by looking at its execution chain:
This explains the TM program that we began with. It corresponds to the description above state for state and edge for edge.
Let us trace the processing of the input string aabb by looking at its execution chain:
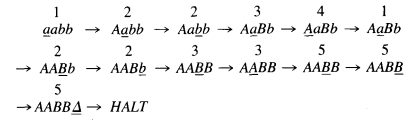
It is clear that any string of the form anbn will reach the HALT state. To show that any string that reaches the HALT state must be of the form anbn we trace backward. To reach HALT we must get to state 5 and read a △. To be in state 5 we must have come from state 3 from which we read an A and some number of B's while moving to the right. So at the point we are in state 3 ready to terminate, the TAPE and TAPE HEAD situation is as shown below:

To be in state 3 means we have begun at START and circled around the loop some number of times
Every time we go from START to state 3 we have converted an a to an A and a b to a B. No other edge in the program of this TM changes the contents of any cell on the TAPE. However many B's there are, there are just as many A's. Examination of the movement of the TAPE HEAD shows that all the A's stretch in one connected sequence of cells starting at cell i.
To go from state 3 to HALT shows that the whole TAPE has been converted to A's then B's followed by blanks. Putting this all together, to get to HALT the input word must be anbn for some n > 0.
Example : Trace the processing of the input string
Consider the following TM
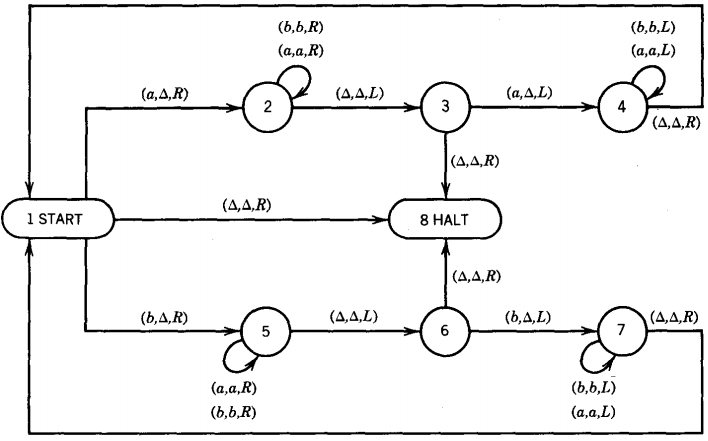
We read the first letter of the input string and erase it, but we remember whether it was an a or a b.
We go to the last letter and check to be sure it is the same as what used to be the first letter. If not, we crash, but if so, we erase it too. We then return to the front of what is left of the input string and repeat the process.
If we do not crash while there are any letters left, then when we get to the condition where the whole TAPE is blank we accept the input string. This means that we reach the HALT state. Notice that the input string itself is no longer on the TAPE. The process, briefly, works like this:
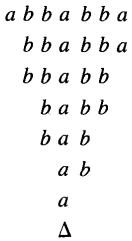
We mentioned above that when we erase the first letter we remember what it was as we march up to the last letter. Turing machines have no auxiliary memory device, like a PUSHDOWN STACK, where we could store this information, but there are ways around this.
One possible method is to use some of the blank space further down the TAPE for making notes. Or, as in this case, the memory comes in by determining what path through the program the input takes.
If the first letter is an a, we are off on the state 2-state 3-state 4 loop. If the first letter is a b, we are off on the state 5-state 6-state 7 loop.
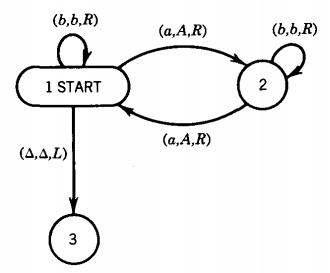
All of this is clear from the descriptions of the meanings of the states below: State 1 When we are in this state, we read the first letter of what is left of the input string. This could be because we are just starting and reading cell i or because we have been returned here from state 4 or state 7.
If we read an a, we change it to a △ (erase it), move the TAPE HEAD to the right, and progress to state 2. If we read a b, we erase it and move the TAPE HEAD to the right and progress to state 5.
If we read a △ where we expect the string to begin, it is because we have erased everything, or perhaps we started with the input word Λ. In either case, we accept the word and we shall see that it is in EVENPALINDROME.
State 2 We get here because we have just erased an a from the front of the input string and we want to get to the last letter of the remaining input string to see if it too is an a. So we move to the right through all the a's and b's left in the input until we get to the end of the string at the first △. When that happens we back up one cell (to the left) and move into state 3.
State 3 We get here only from state 2, which means that the letter we erased at the start of the string was an a and state 2 has requested us now to read the last letter of the string.
We found the end of the string by moving to the right until we hit the first △. Then we bounced one cell back to the left. If this cell is also blank, then there are only blanks left on the TAPE. The letters have all been successfully erased and we can accept the word. So we go to HALT.
If there is something left of the input string, but the last letter is a b, the input string was not a palindrome. Therefore we crash by having no labeled edge to go on. If the last non △ letter is an a, then we erase it, completing the pair, and begin moving the TAPE HEAD left, down to the beginning of the string again to pair off another set of letters.
We should note that if the word is accepted by going from state 3 to HALT then the a that is erased in moving from state 1 to state 2 is not balanced by another erasure but was the last letter left in the erasure process. This means that it was the middle of a word in ODDPALINDROME:
Notice that when we read the △ and move to HALT we still need to include in the edge's label instructions to write something and move the TAPE HEAD somewhere. The label (△, a, R) would work just as well, or (△, B, R).
However, (△, a, L) might be a disaster. We might have started with a one-letter word, say a. State 1 erases this a. Then state 2 reads the △ in cell ii and returns us to cell i where we read the blank. If we try to move left from cell i we crash on the very verge of accepting the input string.
State 4 Like state 2, this is a travel state searching for the beginning of what is left of the input string. We keep heading left fearlessly because we know that cell i contains a △, so we shall not fall off the edge of the earth and crash by going left from cell i. When we hit the first △, we back up one position to the right, setting ourselves up in state 1 ready to read the first letter of what is left of the string:
State 5 We get to state 5 only from state 1 when the letter it has just erased was a b. In other words, state 5 corresponds exactly to state 2 but for strings beginning with a b. It too searches for the end of the string
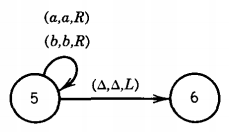
State 6 We get here when we have erased a b in state 1 and found the end of the string in state 5. We examine the letter at hand. If it is an a, then the string began with b and ended with a, so we crash since it is not in PALINDROME. If it is a b, we erase it and hunt for the beginning again.
If it is a △, we know that the string was an ODDPALINDROME with middle letter b. This is the twin of state 3. State 7 This state is exactly the same as state 4. We try to find the beginning of the string.
Putting all these states together, we get the picture we started with. Let us trace the running of this TM on the input string ababa
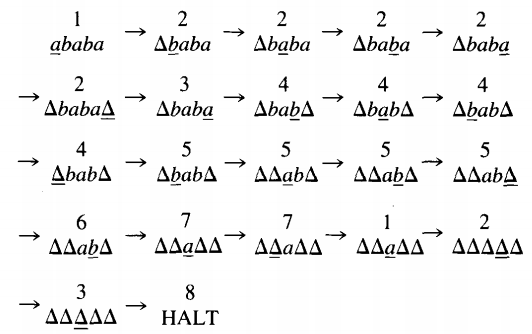
EXAMPLE
Let us build a TM to accept the language EVEN-EVEN-the collection of all strings with an even number of a's and an even number of b's. Let this be our algorithm:
Starting with the first letter let us scan up the string replacing all the a's by A's. During this phase we shall skip over all b's.
Let us make our first replacement of A for a in state 1, then our second in state 2, then our third in state 1 again, and so on alternately until we reach the first blank.
If the first blank is read in state 2, we know that we have replaced an odd number of a's and we must reject the input string. We do this by having no edge leaving state 2 which wants to read the TAPE entry △.
This will cause a crash. If we read the first blank in state 1, then we have replaced an even number of a's and must process b's. This could be done by the program segment below:
Now suppose that from state 3 we go back to the beginning of the string replacing b's by B's in two states: the first B for b in state 3, the next in state 4, then in state 3 again, and so on alternately, all the time ignoring the A's.
If we do this we run into a subtle problem. Since the word starts in cell i, we do not have a blank space to bounce off when we are reading back down the string.
When we read what is in cell i we do not know we are in cell i and we try to move the TAPE HEAD left, thereby crashing. Even the input strings we want to accept will crash.
There are several ways to avoid this. The solution we choose for now is to change the a's and b's at the same time as we first read up the string. This will allow us to recognize input strings of the form EVEN-EVEN without having to read back down the TAPE.
Let us define the four states:
State 1 We have read an even number of a's and an even number of b's.
State 2 We have read an even number of a's and an odd number of b's.
State 3 We have read an odd number of a's and an even number of b's.
State 4 We have read an odd number of a's and an odd number of b's.
If we are in state 1 and we read an a we go to state 3. There is no need to change the letters we read into anything else since one scan over the input string settles the question of acceptance. If we read a b from state 1, we leave it alone and go to state 2 and so on. This is the TM:
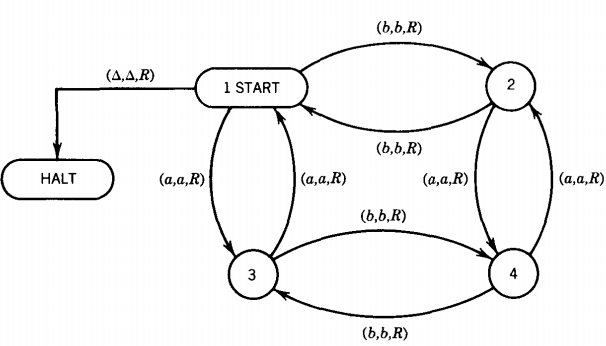
If we run out of input in state 1, we accept the string by going to HALT along the edge labeled (△,△,R).
This machine should look very familiar. It is the FA that accepts the language EVEN-EVEN dressed up to look like a TM.