POST MACHINES



  • In 1936, the same fruitful year Turing introduced the Turing machine, Emil Leon Post (1897-1954) created the Post machine, which he hoped would prove to be the "universal algorithm machine" sought after.


  • One condition that must be satisifed by such a "universal algorithm machine" (we have kept this phrase in quotes because we cannot understand it in a deeper sense until later) is that any language that can be precisely defined by humans (using English or pictures or hand signals) should be accepted (or recognized) by some version of this machine.


  • This would make it more powerful than an FA or a PDA. There are nonregular languages and non-context-free languages, but there should not be any non-Turing or non-Post languages.


  • DEFINITION


    1. A Post machine, denoted PM, is a collection of five things:


    2. 1. The alphabet Y of input letters plus the special symbol #. We generally use Σ = {a,b}


    3. 2. A linear storage location (a place where a string of symbols is kept) called the STORE, or QUEUE, which initially contains the input string. This location can be read, by which we mean the left-most character can be removed for inspection. The STORE can also be added to, which means a new character can be concatenated onto the right of whatever is there already. We allow for the possibility that characters not in Σ can be used in the STORE, characters from an alphabet Γ called the store alphabet.


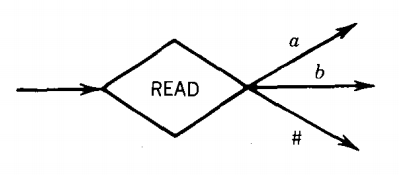
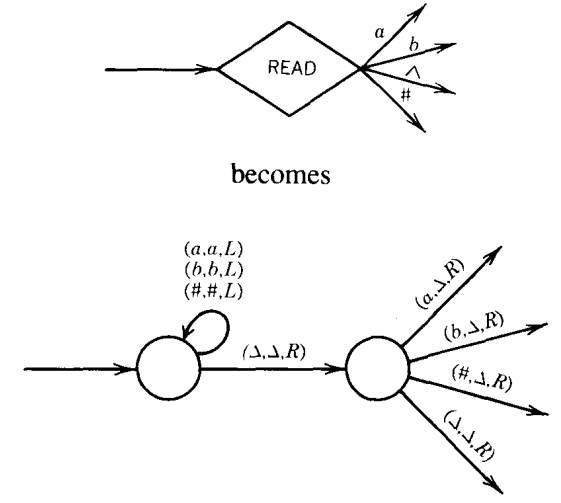
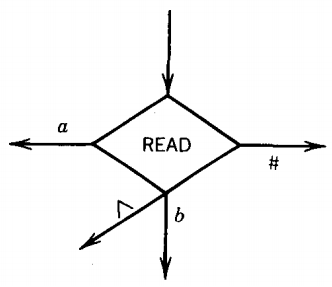
    4. 3. READ states, for example post-machine


    5. which remove the left-most character from the STORE and branch accordingly. The only branching in the machine takes place at the READ states. There may be a branch for every character in Σ or Γ. Note the A branch that means that an empty STORE was read. PM's are deterministic, so no two edges from the READ have the same label.


    6. 4. ADD states:


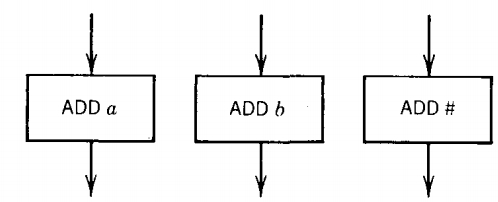
    7. post-machine


    8. which concatenate a character onto the right end of the string in STORE. This is different from PDA PUSH states, which concatenate characters onto the left. Post machines have no PUSH states. No branching can take place at an ADD state. It is possible to have an ADD state for every letter in Σ and Γ.


    9. 5. A START state and some halt states called ACCEPT and REJECT:


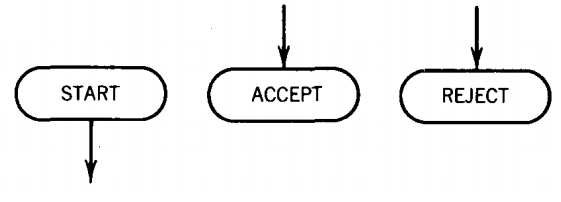
    10. post-machine


    11. If we are in a READ state and there is no labeled edge for the character we have read then we crash, which is equivalent to taking a labeled edge into a REJECT state. We can draw our PM's with or without REJECT states.




Post machine



  • The STORE is a first-in first-out or FIFO stack in contradistinction to a PUSHDOWN or LIFO STACK. The contents of an originally empty STORE after the operations


  • post-machine


  • is the string : abb


  • If we then read the STORE, we take the a branch and the STORE will be reduced to bb.


  • A Post machine does not have a separate INPUT TAPE unit. In processing a string, we assume that the string was initially loaded into the STORE and we begin executing the program from the START state on.


  • If we wind up in an ACCEPT state, we accept the input string. If not, not. At the moment we accept the input string the STORE could contain anything.


  • It does not have to be empty nor need it contain the original input string. As usual, we shall say that the language defined (or accepted) by a Post machine is the set of strings that it accepts. A Post machine is yet another language recognizer or acceptor.


  • As we have defined them, Post machines are deterministic, that is, for every input string there is only one path through the machine; we have no alternative at any stage.


  • We could also define a nondeterministic Post machine, NPM. This would allow for more than one edge with the same label to come from a READ state.


  • It is a theorem that, in their strength as language acceptors, NPM = PM.




EXAMPLE



  • Consider the PM below:


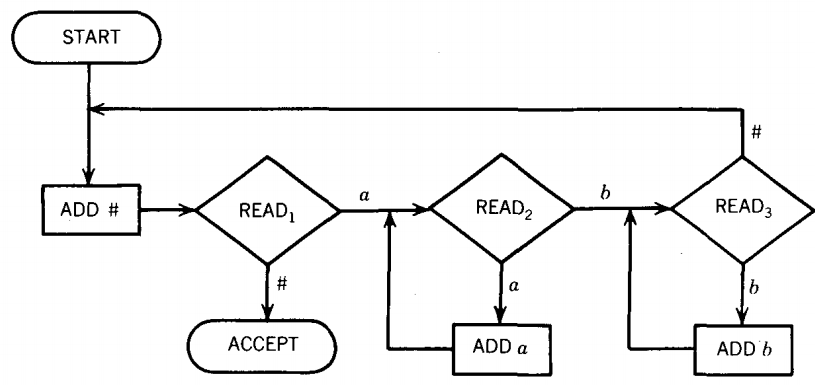
  • post-machine


  • As required by our definition, this machine is deterministic. We have not drawn the edges that lead to REJECT states but instead we allow the path to crash in the READ state if there is no place for it to go.


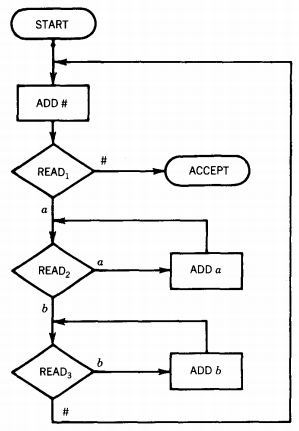
  • Let us trace the processing of the input aaabbb on this PM.


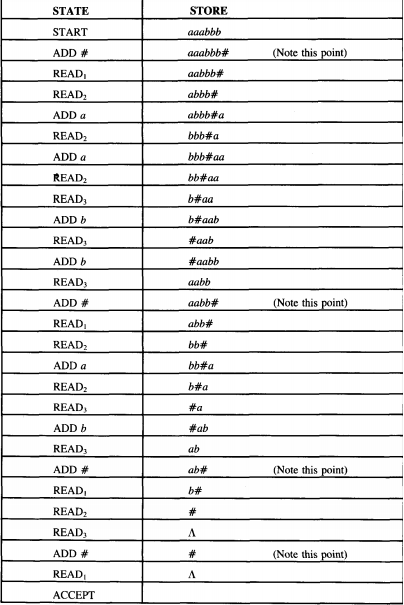
  • post-machine


  • The trace makes clear to us what happens. The # is used as an end-ofinput string signal (or flag). In READ1 we check to see if we are out of input;


  • that is, are we reading the end-of-input signal #? If so, we accept the string. If we read a b, the string crashes.


  • So nothing starting with a b is accepted. If the string starts with an a, this letter is consumed by READ1 ; that is the trip from READ1 to READ2 costs one a that is not replaced.


  • The loop at READ2 puts the rest of the a's from the front cluster of a's behind the #.


  • The first b read is consumed in the trip from READ2 to READ3.


  • At READ3 the rest of the first cluster of b's is stripped off the front and appended onto the back, behind the a's that are behind the #.


  • After the b's have been transported we expect to read the character #. If we read an a, we crash.


  • To survive the trip back from READ3 to ADD # the input string must have been originally of the form a*b*.


  • In each pass through the large circuit READ1-READ2 -READ 3-READ 1 , the string loses an a and a b. Note the markers we have indicated along the side.


  • To be accepted, both a's and b's must run out at the same time, since if there were more a's than b's the input string would crash at READ2 by reading a # instead of a b, and if the input string had more b's than a's, it would crash in state READ1 by reading a b.


  • Therefore the language accepted by this PM is {anbn} (in this case including Λ).




EXAMPLE



  • Consider the PM below:


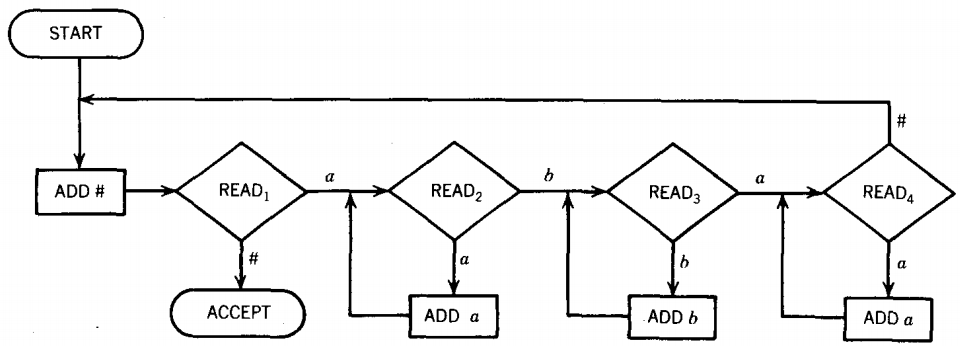
  • post-machine


  • This machine is very much like the PM in the previous example. We start with a string in the STORE. We add a # to the back of it. We accept it in state READ1, if the string was initially empty. If it starts with a b, we crash.


  • If it starts with an a, we use up this letter getting to READ2. Here we put the entire initial clump of a's (all the way up to the first b) behind the #. We read the first b and use it up getting to READ3.


  • Here we put the rest of the clump of b's behind the a's behind the #. We had then better read another a to get to READ4.


  • In READ4 a bunch of a's (minus the one it costs to get there) are placed in the store on the right, behind the b's that are behind the a's that are behind the #.


  • After we exhaust these a's, we had better find a # or we crash. After reading the # off the front of the STORE we replace it at the back of the STORE in the state ADD #.


  • To make this return to ADD #, the input string must originally have been of the form a*b*a*. Every time through this loop we use up one a from the first clump, one b from the b clump, and one a from the last clump.


  • The only way we ever get to ACCEPT is to finish some number of loops and find the STORE empty, since after ADD # we want to read # in state READ1.


  • This means that the three clumps are all depleted at the same time, which means that they must have had the same number of letters in them initially.


  • This means that the only words accepted by this PM are those of the form {anbnan}.




THEOREM



  • Any language that can be accepted by a Post machine can be accepted by some Turing machine.


  • PROOF


    1. As with many theorems before, we prove this one by constructive algorithm. In this case we show how to convert any Post machine into a Turing machine, so that if we have a PM to accept some language we can see how to build a TM that will process all input strings exactly the same way as the PM, leading to HALT only when the PM would lead to ACCEPT.


    2. We know that PM's are made up of certain components, and we shall show how to convert each of these components into corrresponding TM components that function the same way. We could call this process simulating a PM on a TM.


    3. The easiest conversion is for the START state, because we do not change it at all. TM's also begin all execution at the START state.


    4. The second easiest conversion is for the ACCEPT state. We shall rename it HALT because that is what the accepting state is called for TM's.


    5. The next easiest conversion is for the REJECT states. TM's have no reject states, they just crash if no path can be found for the letter read by the TAPE HEAD. So we simply delete the REJECT states. (We often do this for PM's too.)


    6. Now before we proceed any further, we should address the question of converting the PM's STORE into the TM's TAPE.


    7. The STORE contains a string of letters with the possibility of some occurrences of the symbol #. Most often there will be only one occurrence of the symbol # somewhere in the middle of the string, but even though this is usual in practice, it is not demanded by the definition.


    8. We have seen the # used as a marker of the end of the original input, but the definition of PM's allows us to put any number of them in the STORE.


    9. We now describe how we can use the TM TAPE to keep track of the STORE. Suppose the contents of the STORE look like \( x_1 x_2 x_3 x_4 x_5 \)


    10. where the x's are from the PM input alphabet Σ or the symbol # and none of them is △. We want the corresponding contents of the TM TAPE to b


    11. post-machine


    12. with the TAPE HEAD pointing to one of the x's. Notice that we keep some △'s on the left of the STORE information, not just on the right, although there will only be finitely many △'s on the left, since the TAPE ends in that direction.


    13. We have drawn the TM TAPE picture broken because we do not know exactly where the x's will end up on the TAPE. The reason for this is that the PM eats up stuff from the left of the STORE and adds on stuff to the right. If at some point the STORE contains abb and we execute the instructions


    14. READ - ADD a - READ - ADD a - ADD b - READ


    15. the TM TAPE will change like this:


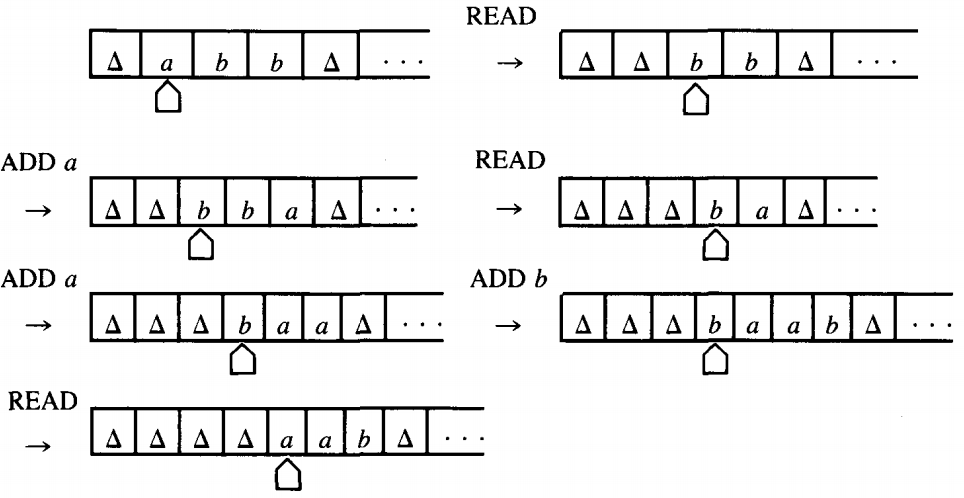
    16. post-machine


    17. The non-△ information wanders up to the right while △'s accumulate on the left.


    18. Immediately after the START state on the TM we shall employ the preprocessor INSERT to insert a △ in cell i and to move the whole non-△ initial input string one cell to the right up the TAPE.


    19. We do this so that the first PM operation simulated is like all the others in that the non-△ information on the TM TAPE has at least one △ on each side of it, enabling us to locate the right-most and left-most ends of the input string by bouncing off △'s.


    20. There are two operations by which the PM changes the contents of the STORE: ADD and READ. Let us now consider how a TM can duplicate the corresponding actions on its TAPE.


    21. If the PM at some point executes the state


    22. post-machine


    23. the TM must change its TAPE from something like


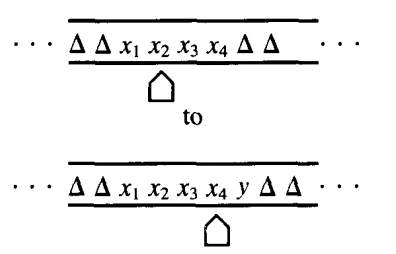
    24. post-machine


    25. To do this, the TAPE HEAD must move to the right end of the non-△ characters, locate the first △ and change it to y. This can be done as follows:


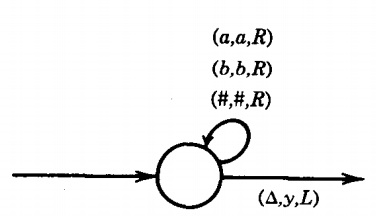
    26. post-machine


    27. We have illustrated this in the case where Σ = {a,b}, but if Y. had more letters it would only mean more labels on the loop. Notice also that we have left the TAPE HEAD again pointing to some non-△ character. This is important.


    28. We do not want the TAPE HEAD wandering off into the infinitely many blanks on the right.


    29. There is only one other PM state we have to simulate; that is the READ state. The READ state does two things. It removes the first character from the STORE and it branches in accordance with what it has removed. The other states we have simulated did not involve branching.


    30. For a TM to remove the left-most non-△ character, the TAPE HEAD must move leftward until the first blank it encounters. It should then back up one cell to the right and read the non-△ character in that cell. This it must turn into a △ and move itself right, never moving beyond the string of non-A's. This process will require two states in the TM:


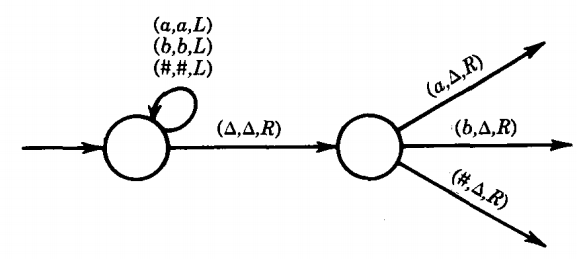
    31. post-machine


    32. Notice that we leave the second state along different edges, depending on which character is being erased. This is equivalent to the PM instruction


    33. post-machine


    34. We should also note that because we were careful to insert a △ in cell i in front of the input string we do not have to worry about moving the TAPE HEAD left from cell i and crashing while searching for the △ on the left side.


    35. If while processing a given input the STORE ever becomes empty, then the TM TAPE will become all △'s. It is possible that the PM may wish to READ an empty STORE and branch accordingly. If this alternative is listed in the PM, it should also be in the TM.


    36. post-machine


    37. If the TAPE is all △'s, the TAPE HEAD reads the cell it is pointing to, which contains a △, and moves to the right, "thinking" that it is now in the non △ section of the TAPE.


    38. It then reads this cell and finds another △, which it leaves as a △ and moves right again. The program branches along the appropriate edge. Just because the STORE is empty does not mean that the program is over.


    39. We might yet ADD something and continue. The TM simulation can do the same.


    40. Thus we can convert every PM state to a TM state or sequence of states that have the same function. The TM so constructed will HALT on all words that the PM sends to ACCEPT.


    41. It will crash on all words that the PM sends to REJECT (or on which the PM crashes), and it will loop forever on those same inputs on which the PM loops forever




EXAMPLE



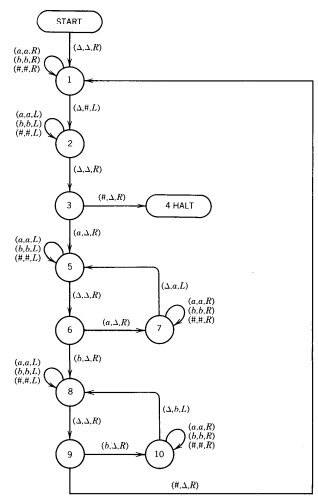
  • post-machine


  • This PM accepts the language {anbn}. This time we have drawn the machine vertically to facilitate its conversion into a TM.


  • Following the algorithm in the proof, we produce the next machine, where, for the sake of simplicity, we have omitted the △-inserting preprocessor and assume that the input string is placed on the TM TAPE starting in cell ii with a △ in cell i.


  • post-machine


  • Thus, we get


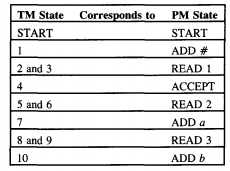
  • post-machine


  • In the example above, we see that edges between the independently simulated states always have TM labels determined from the PM.


  • In the TM we just constructed we have encountered a situation that plagues many Turing machines: piles of tedious multiple-edge labels that all say about the same thing:


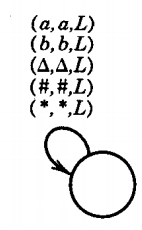
  • post-machine


  • This is proper Turing machine format for the instruction "If we read an a, a b, a △, a #, or a *, leave it unchanged and move the TAPE HEAD left." Let us now introduce a shortened form of this sentence: (a,b,△,#,*;= ,L)




DEFINITION



  • If a, b, c, d, e are TM TAPE characters, then (a,b,c,d,e; = ,L) stands for the instructions (a,a,L) (b,b,L) ... (e,e,L)


  • Similarly we will employ (a,b,c,d,e;=,R) for the set of labels (a,a,R) (b,b,R)... (e,e,R) Let us trace the processing of the input string aabb:


  • post-machine


  • Here we have decided that the initial △'s from cell i up to the data are significant and have included them in the trace.


  • We can see from this execution chain that this is a TM that accepts {anbn}.


  • We already know that there are other (smaller) TM's that do the same job.


  • The algorithm never guaranteed to find the best TM that accepts the same language, only to prove the existence of one such by constructive algorithm.