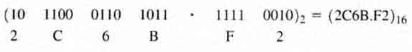Digital systems
A characteristic of digital systems is their ability to represent and manipulate discrete elements of information. Any set that is restricted to a finite number of elements contains discrete information.
Examples of discrete sets are the 10 decimal digits. the 26 letters of the alphabet the 52 playing cards. Early digital computers were used for numeric computations. In this case. the discrete elements were the digits. From this application the term digital computer emerged.
Discrete elements of information are represented in a digital system by physical quantities called signals.
Electrical signals such as voltages and currents arc the most common . Electronic devices called transistors predominate in the circuitry that implements these signals. The signals in most present day electronic digital systems use just two discrete values and are the therefore said to be binary.
A binary digit is called a bit. It has two values: 0 and I. Discrete elements of information are represented with groups of bits called binary codes.
A major trend in digital design methodology is the use of a hardware description language(HDL) to describe and simulate the functionality of a digital circuit.
An HDL resembles a programming language and is suitable for describing digital circuits in textual form. It is used to simulate a digital system to verify its operation before hardware is built in. It is also used in conjunction with logic synthesis tools to automate the design process.
Digital circuits are also referred to as logic circuits. They process data by means of binary logic elements (logic gates) using binary signals. Quantities are stored in binary (two- valued) storage elements (flip-flops).
Binary Number Systems
A decimal number is reresented by the convention.
\( a_5a_4a_3a_2a_1a_0.a_{-1}a_{-2}a_{-3} \)
The coefficients aj are any digits (0 - 9) and the subscript value 'j' gives the place value and hence the power of 10 by which the coefficient must he multiplied. Thus, the preceding decimal number can he expressed as
\( 10^5a_5 + 10^4a_4 + 10^3a_3 + 10^2a_2 + 10^1a_1 + 10^0a_0 + 10^{-1}a_{-1} + 10^{-2}a_{-2} + 10^{-3}a_{-3} \)
The decimal number system is said be of base, or radix = 10 because it uses 10 digits and the coefficients are multiplied by powers of 10.
The binary system is a different number system. The coefficients of the binary number system have only two [possible values: 0 and 1].
Each coefficient aj is multiplied by 2j and the results are added to obtain the decimal equivalent of the number. The radix point ( e.g .. the decimal point when 10 is the radix) distinguishes positive powers of 10 from negative powers of 10.
Example: Binary number 11010.11 in decimal form is expressed as:
\( 1 * 2^4 + 1 * 2^3 + 0 * 2^2 + 1 * 2^1 + 0 * 2^0 + 1 * 2^{-1} + 1 * 2^{-2} = 26.75\)
In general a number of base 'r' is expressed as:
\( r^na_n + r^{n-1}a_{n-1} + r^{n-2}a_{n-2} + r^{n-3}a_{n-3} + ... + r^{1}a_{1} + r^{0}a_{0} + r^{-1}a_{-1} + r^{-2}a_{-2} + ... + r^{-m}a_{-m} \)
The coefficients aj range in value from 0 to r - 1.
Example: Base-5 number (4021.2)5 in decimal form is expressed as:
\( 4 * 5^3 + 0 * 5^2 + 2 * 5^1 + 1 * 5^0 + 2 * 5^{-1} = (511.40)_{10} \)
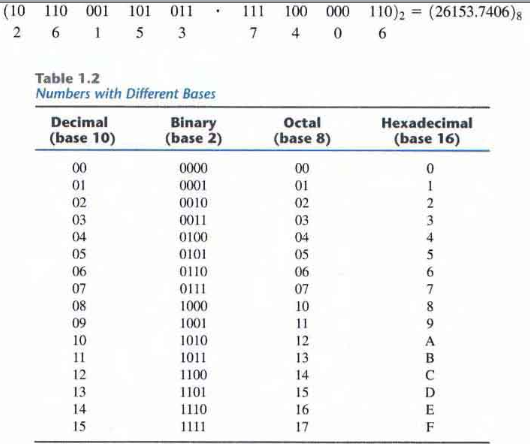
Example: Octal number (127.4)8 in binary form is expressed as:
\( 1 * 8^2 + 2 * 8^1 + 7 * 8^0 + 4 * 8^{-1} = (87.5)_{10}\)
Example: Hexadecimal number (B65F)16 in binary form is expressed as:
\( 11 * 16^3 + 6 * 16^2 + 5 * 16^1 + 15 * 16^0 = (46687)_{10}\)
Binary Arithmetic Rules
Rules of Binary Addition
- 0 + 0 = 0
- 0 + 1 = 1
- 1 + 0 = 1
- 1 + 1 = 0, and carry 1 to the next more significant bit
For example,
| 00011010 + 00001100 = 00100110 | 1 1 | carries | ||
| 0 0 0 1 1 0 1 0 | = | 26(base 10) | ||
| + 0 0 0 0 1 1 0 0 |
= | 12(base 10) | ||
| 0 0 1 0 0 1 1 0 | = | 38(base 10) | ||
| |
||||
| 00010011 + 00111110 = 01010001 | 1 1 1 1 1 | carries | ||
| 0 0 0 1 0 0 1 1 | = | 19(base 10) | ||
| + 0 0 1 1 1 1 1 0 |
= | 62(base 10) | ||
| 0 1 0 1 0 0 0 1 | = | 81(base 10) | ||
Note: The rules of binary addition (without carries) are the same as the truths of the XOR gate.
Rules of Binary Subtraction
- 0 - 0 = 0
- 0 - 1 = 1, and borrow 1 from the next more significant bit
- 1 - 0 = 1
- 1 - 1 = 0
For example,
| 00100101 - 00010001 = 00010100 | 0 | borrows | ||
| 0 0 |
= | 37(base 10) | ||
| - 0 0 0 1 0 0 0 1 |
= | 17(base 10) | ||
| 0 0 0 1 0 1 0 0 | = | 20(base 10) | ||
| |
||||
| 00110011 - 00010110 = 00011101 | 0 10 1 | borrows | ||
| 0 0 |
= | 51(base 10) | ||
| - 0 0 0 1 0 1 1 0 |
= | 22(base 10) | ||
| 0 0 0 1 1 1 0 1 | = | 29(base 10) | ||
Rules of Binary Multiplication
- 0 x 0 = 0
- 0 x 1 = 0
- 1 x 0 = 0
- 1 x 1 = 1, and no carry or borrow bits
For example,
| 00101001 × 00000110 = 11110110 | 0 0 1 0 1 0 0 1 | = | 41(base 10) | |
| × 0 0 0 0 0 1 1 0 |
= | 6(base 10) | ||
| 0 0 0 0 0 0 0 0 | ||||
| 0 0 1 0 1 0 0 1 | ||||
| 0 0 1 0 1 0 0 1 |
||||
| 0 0 1 1 1 1 0 1 1 0 | = | 246(base 10) | ||
| |
||||
| 00010111 × 00000011 = 01000101 | 0 0 0 1 0 1 1 1 | = | 23(base 10) | |
| × 0 0 0 0 0 0 1 1 |
= | 3(base 10) | ||
| 1 1 1 1 1 | carries | |||
| 0 0 0 1 0 1 1 1 | ||||
| 0 0 0 1 0 1 1 1 |
||||
| 0 0 1 0 0 0 1 0 1 | = | 69(base 10) | ||
Binary Division
Binary division is the repeated process of subtraction, just as in decimal division.
For example,
| 00101010 ÷ 00000110 = 00000111 | 1 | 1 | 1 | = | 7(base 10) | ||||||||
| 1 1 0 | ) | 0 | 0 | | 10 | 1 | 0 | 1 | 0 | = | 42(base 10) | ||
| - | 1 | 1 | 0 | = | 6(base 10) | ||||||||
| 1 | borrows | ||||||||||||
| | 10 | 1 | |||||||||||
| - | 1 | 1 | 0 | ||||||||||
| 1 | 1 | 0 | |||||||||||
| - | 1 | 1 | 0 | ||||||||||
| 0 | |||||||||||||
| |
|||||||||||||
| 10000111 ÷ 00000101 = 00011011 | 1 | 1 | 0 | 1 | 1 | = | 27(base 10) | ||||||
| 1 0 1 | ) | | | | 10 | 0 | 1 | 1 | 1 | = | 135(base 10) | ||
| - | 1 | 0 | 1 | = | 5(base 10) | ||||||||
| 1 | | 10 | |||||||||||
| - | 1 | 0 | 1 | ||||||||||
| 1 | 1 | ||||||||||||
| - | 0 | ||||||||||||
| 1 | 1 | 1 | |||||||||||
| - | 1 | 0 | 1 | ||||||||||
| 1 | 0 | 1 | |||||||||||
| - | 1 | 0 | 1 | ||||||||||
| 0 | |||||||||||||
Number Conversion: Converting a decimal to a number of base 'r'.
The conversion of a decimal integer to a number in base 'r' is done by dividing the number and all successive quotients by 'r' and accumulating the remainders.
| Integer | Quotient | Remainder | Coefficient 'aj' |
|---|---|---|---|
| 153 / 8 = | 19 | 1 | a0 = 1 |
| 19 / 8 = | 2 | 3 | a1 = 3 |
| 2/8 = | 0 | 2 | a2 = 2 |
Therefore, the answer of (153)10 = \( a_2a_1a_0 \) = (231) 8.
Q.Convert decimal (0.6875)10 to binary.
| Step | Integer | Fraction | Coefficient 'aj' |
|---|---|---|---|
| 0.6875 * 2= | 1 | 0.375 | a-1 = 1 |
| 0.3750 * 2 = | 0 | 0.75 | a-2 = 0 |
| 0.75 * 2 = | 1 | 0.5 | a-3 = 1 |
| 0.5 * 2 = | 1 | 0 | a-4 = 1 |
Therefore, the answer of (0.6875)10 = \( (0.a_{-1}a_{-2}a_{-3}a_{- 4})_2 \) = \( (0.1011)_2 \). To convert a decimal fraction to a number expressed in base 'r', a similar procedure is used. However. multiplication is by 'r' instead of 2 and the coefficients found from the Integers may range in value from 0 to r - 1 instead of 0 and 1.
Q.Convert decimal (0.513)10 to octal.