Subtraction using 1's complement
When we subtract M - N then 'M' is referred to as 'Minuend' and 'subtraend' respectively.
We take the 1's complement of N and add it to M. Then if carry is obtained we discard it and add 1 to the result. This is the final answer.
In case no carry is generated we take the 1's complement of the result and add minus sign to it. This is the final answer.
Q. Using 1's complement get 1010100 - 1000011

Q. Using 1's complement get 1000011 - 1010100

SIGNED BINARY NUMBERS
Positive integers (including zero) can be represented as unsigned numbers. However, to represent negative integers, we need a notation for negative values.
It is customary to represent the sign with a bit placed in the leftmost position of the number. The convention is to make the sign bit 0 for positive and 1 for negative.
If the binary number is signed, then the leftmost bit represents the sign and the rest of the bits represent the number.
If the binary number is assumed to be unsigned, then the left most bit is the most significant bit of the number.
- Example of unsigned number:
01001 can be 9 (unsigned bit) or +9 (signed bit)
- Example of signed number:
11001 can be considered as 25 (unsigned) and -9 (signed number) representation.
When arithmetic operations are implemented in a computer, it is more convenient to use the signed-complement system, for representing negative numbers.
In this system, a negative number is represented by its complement.
1's complement or 2's complement may be used but 2's complement is more common.
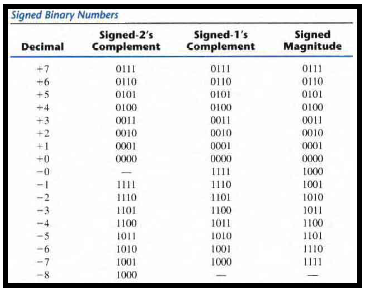
- Binary representation of +9:
00001001
- signed-magnitude representation of -9:
10001001
- signed- 1's-complement representation of -9:
11110110
- signed- 2's-complement representation of -9:
11110111
Points to Remember
In signed-magnitude representation - 9 is obtained from +9 by changing the sign bit in the leftmost position from 0 to 1.
In signed-1's complement, - 9 is obtained by complementing all the bits of +9, including the sign bit.
The signed-2's-complement representation of - 9 is obtained by taking the 2' s complement of the positive number, including the sign bit.
Positive numbers in all three representations are: identical and have 0 in the leftmost position.
The signed-2's complement system has only one representation for 0 which is always positive.
Signed 1's complement and signed magnitude systems have two representations for 0 i.e. +0 and -0.
All negative numbers have a '1' in the leftmost bit position
In the signed- magnitude and the 1's-complement representations there are eight positive numbers and eight negative numbers including two zeros. In the 2's-complement representation there are eight positive numbers, including one zero and eight negative numbers.
The signed-complement system is normally used in computer arithmetic.
Arithmetic Addition
The addition of two numbers in the signed-magnitude system follows the rules of ordinary arithmetic.
If the signs are the same, we add the two magnitudes and give the sum the common sign.
If the signs are different, we subtract the smaller magnitude from the larger and give the difference the sign of the larger magnitude.
For example, (+15) + ( - 20) = -(20 - 15) = - 5 and is done by subtracting the smaller magnitude, 15 from the larger magnitude 20 and appending the sign of 20 to the result.
Addition of two signed Binary Numbers
Negative numbers must be initially in 2's-complement form and that if the sum obtained after the addition is negative, it is in 2's-complement form
Any carry out of the sign-bit position is discarded

Arithmetic Subtraction
Take the 2's complement of the subtrahend (including the sign bit) and add it to the minuend ( including the sign bit ). A carry out of the sign-bit position is discarded .
Binary numbers in the signed-complement system are added and subtracted by the same basic addition and subtraction rules as unsigned numbers. Therefore, computers need only one common hardware circuit to handle both types of arithmetic
Note: Negative numbers must be in 2's complement form for this rule to be applicable.
Q: Solve ( - 6 ) - ( -13 )
In binary with eight bits, this operation is written as ( 11111010 - 11110011 )
The subtraction is changed to addition by taking the 2' s complement of the subtrahend (-13), giving ( + 13)
In binary, this is 11111010 + 00001101 = 100000111 Removing the end carry, we obtain the correct answer: 00000111 (+7)
BINARY CODED DECIMAL
A binary code will have some unassigned bit combinations if the number of elements in the set is not a multiple power of 2.
For example, if 10 numbers are to be represented in binary form we will need at least 4 bits and so we can form 24 combination i.e. 16 possibilities.
However, we have 6 possibilities remaining in such a scheme.
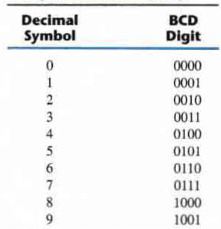
Different binary codes can be obtained by arranging four bits into 10 distinct combinations. The code most commonly used for the decimal digits is the straight binary assignment listed below. This scheme is called binary-coded-decimal and is commonly referred to as BCD
A number with k decimal digits will require 4k bits in BCD.
Each digit in decimal is represented in BCD by a group of 4 bits of binary. A decimal number in BCD is the same as its equivalent binary number only when the number is between 0 and 9.
Moreover, the binary combinations 1010 through 1111 are not used and have no meaning in BCD.
Example: (185)10 = (0001 1000 0101)BCD = (10111001)2
The BCD value has 12 bits to encode the characters of the decimal value. But the equivalent binary number needs only 8 bits. The representation of a BCD number needs more bits then its equivalent binary value . However, there is an advantage in the use of decimal numbers because computer input and output data are generated by people who use the decimal system.
BCD numbers are decimal numbers and not binary numbers even though they are represented in 0/1 form.
Rules of Addition - BCD
Step 1: The given numbers are to be added using the rule of binary addition.
Step 2: If the result of addition of two binary number is greater than 9, which is not valid for BCD number then we add (0110)2 to the sum obtained. This will give the correct result.
Step 3: If the result of addition of two binary number is less than 9, do nothing. The answer is in valid BCD.

Example 1: Produces a value less than 9 so it is correct BCD and no further calculations needed
Example 2: Produces a sum greater than 9 and no carry and so we add (0110)2 to the result to get valid BCD. The result obtained is 10010 and isnt in binary form but BCD and should be interpreted as (0001 0010) i.e. (12)10.
Example 3: Produces a carry and a sum greater than 9, so we add (0110)2 to the result to get valid BCD. The result obtained is 10111 and isnt in binary form but BCD and should be interpreted as (0001 0111) i.e. (17)10.
Other Decimal Codes
BCD (8421): The digits of BCD have the weights 8421 and so a number 0110 is interpreted as 8 * 0 + 4 * 1 + 2 * 1 + 1 * 0 = 6. This is decimal number 6.
Code (2421): Similarly, the same number 1100 in this scheme is weighted as 2 * 1 + 4 * 1 + 2 * 0 + 1 * 0 = 6. This is decimal number 6. Note that some digits can be coded in two possible ways in the 2421 code . For instance decimal 4 can be assigned to bit combination 0100 or 1010 since both combinations add up to a total weight of 4.
Excess - 3: This scheme is an unweighted code in which each coded combination is obtained from the corresponding binary value plus 3.
8 4 -2 -1: This code is an example of assigning both positive and negative weights to a decimal code. In this case, the bit combination 0110 is interpreted as decimal 2 and is calculated from 8 * 0 + 4 * 1 + (-2) * 1 + (-1) * 0 = 2.
Excess 3 and 2421 codes are self complementing as 9's complement of a decimal number is obtained directly by changing 1's to 0's and 0's to 1's.
BCD isnt a self complementing code.
Gray Codes
The output data of many physical systems are quantities that are continuous. These data must be converted into digital form before they are applied to a digital system. Continuous or analog information is converted into digital form by means of an analog-to-digital converter.
Gray code is convenient to use to represent digital data that has been converted from analog form as only one bit changes in going from a number to the next.

Additional Notes
Many applications of digital computers require the handling not only of numbers but also of other characters or symbols such as the letters of the alphabet. The standard binary code for the alphanumeric characters is the American Standard Code for Information Interchange (ASCII), which uses seven bits to code 128 characters.
To detect errors in data communication and processing an eighth bit is sometimes added to the ASCII character to indicate its parity. A parity bit is an extra bit included with a message to make the total number of 1's either even or odd.
As shown above, we insert an extra 1 to make the 1's present in the code to even number (in case of even parity) or odd number (in case of odd parity).
At the receivers end, if the parity check is violated then it means that either 1 / 3 / 5 or odd combination of errors have occured in the characters that were transmitted.
An even combination of errors however goes undetected and additional error detection codes may he needed to take care of that possibility.
Binary Cell: A device that possesses two stable states and is capable of storing one bit (0 or 1) of information.
Register: A register is a group of binary cells. A register with n cells can store any discrete quantity of information that contains n bits. The state of a register is an n-tuple of 1's and 0's with each bit designating the state of one cell in the register

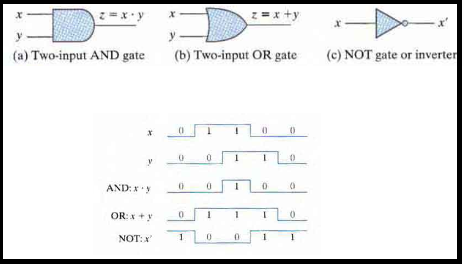
Boolean Gates
Binary logic deals with variables that take on two discrete values and with operations that assume logical meaning.
Logic gates are electronic circuits that operate on one or more input signals to produce an output signal.
For example a particular digital system may define logic 0 as a signal equal to 0 volts and logic 1 as a signal equal to 3 volts.