Extended E-R Features - Specialization

• An entity set may include sub-groupings of entities that are distinct in some way from other entities in the set. For instance, a subset of entities within an entity set may have attributes that are not shared by all the entities in the entity set.




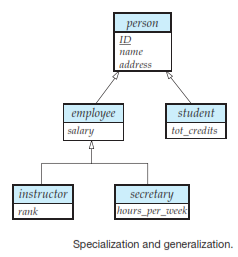
• As an example, the entity set person may be further classified as one of the following: employee, student.




• Each of these person types is described by a set of attributes that includes all the attributes of entity set person plus possibly additional attributes.




• The process of designating sub-groupings within an entity set is called specialization.




• For example, : A university divides students into two categories: graduate and undergraduate. Graduate students have an office assigned to them. Undergraduate students are assigned to a residential college. Each of these student types is described by a set of attributes that includes all the attributes of the entity set student plus additional attributes.




• An entity set may be specialized by more than one distinguishing feature. A distinguishing feature among employee entities is the job the employee performs.




• In terms of an E-R diagram, specialization is depicted by a hollow arrow-head pointing from the specialized entity to the other entity. This relationship is the ISA relationship, which stands for “is a” and represents, for example, that an instructor “is a” employee.




• Types of specialization :




1. overlapping specialization : An entity may belong to multiple specialized entity sets.




2. disjoint specialization : An entity may belong to at most one specialized entity sets.





• For an overlapping specialization (as is the case for student and employee as specializations of person), two separate arrows are used. For a disjoint specialization (as is the case for instructor and secretary as specializations of employee), a single arrow is used.




• The specialization relationship may also be referred to as a superclass - subclass relationship.

Generalization

• The design process can proceed in a bottom-up manner, in which multiple entity sets are synthesized into a higher-level entity set on the basis of common features.




• Suppose we have two entities intructor (instructor_id, instructor_name, instructor_salary, rank) and secretary (secretary_id, secretary_name, secretary_salary, hours_per_week).




• Since there are multiple common attributes in the two relations , this commonality can be expressed by generalization.




• To create a generalization, the attributes must be given a common name and represented with the higher-level entity person.

Attribute Inheritance

• A crucial property of the higher - and lower-level entities created by specialization and generalization is attribute inheritance.




• The attributes of the higher-level entity sets are said to be inherited by the lower-level entity sets.




• For example, Consider relations student and employee inheriting the attributes of person. Thus, student is described by attributes of super-class as well as its own attributes.




• This also extends to participation inheritance which means that if a base class participates in a relationship set then its sub-classes also participate in that relationship set.

Constraints on Generalizations

• Condition-defined :




1. In condition-defined lower-level entity sets, membership is evaluated on the basis of whether or not an entity satisfies an explicit condition or predicate.




2. For example : Suppose there is an entity called student which has attribute education_status which can take values {undergraduate, postgraduate, graduate}. This would decide the subclass to which a student belongs.




3. Since all the lower-level entities are evaluated on the basis of the same attribute (in this case, on student type), this type of generalization is said to be attribute-defined.




• User-defined :




1. The database user decides a condition on basis of which a particular entry or tuple in the relation shall be classified in the sub-classes.




2. For example: The user may decide to assign an employee to a particular type of department based on his performance seen over a period of three months.




3. So there is no explicit condition but the individuals are assigned on a case to case basis.




• Coverage based :




1. A disjointness constraint requires that an entity belong to no more than one lower-level entity set.




2. In overlapping generalizations, the same entity may belong to more than one lower-level entity set within a single generalization.




• Completeness based :




1. Total generalization or specialization : Each higher-level entity must belong to a lower-level entity set.




2. Partial generalization or specialization : Some higher-level entities may not belong to any lower-level entity set.

Points to Remember :

• Partial generalization is the default.




• To specify total generalization in an E-R diagram we add the keyword “total” in the diagram and draw a dashed line from the keyword to the corresponding hollow arrow-head to which it applies to.




• When a total completeness constraint is in place, an entity inserted into a higher level entity set must also be inserted into at least one of the lower-level entity sets.




• With a condition-defined constraint, all higher-level entities that satisfy the condition must be inserted into that lower-level entity set.




• An entity that is deleted from a higher-level entity set also is deleted from all the associated lower-level entity sets to which it belongs.

Atomic Domains and First Normal Form

• A domain is atomic if elements of the domain are considered to be indivisible units. We say that a relation schema R is in first normal form (1NF) if the domains of all attributes of R are atomic.




• For example : Consider an organization that assigns employees identification numbers of the following form: The first two letters specify the department and the remaining four digits are a unique number within the department for the employee such as “CS001” and “EE1127”.




• Such identification numbers can be divided into smaller units, and are therefore nonatomic. If a relation schema had an attribute whose domain consists of identification numbers encoded as above, the schema would not be in first normal form.




• When an employee of such an organization changes departments, the employee’s identification number must be changed everywhere it occurs, which can be a difficult task.

Functional Dependencies

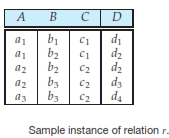
• Consider a relation given by below diagram:





• To check whether A → C we see if every value of A has a unique value in C i.e. A[a₁] = c₁, A[a₂] = c₂, A[a₃] = c₃. Thus we say A → C.




• But this does not mean that C → A as C[c₂] = a₂ and a₃ which means that it does not have a unique value.




• Some functional dependencies are said to be trivial because they are satisfied by all relations. For example, A → A is satisfied by all relations involving attribute A.




• Similarly, AB → A is satisfied by all relations involving attribute A. In general, a functional dependency of the form α → β is trivial if β ⊆ α.

Closure ( F⁺ ) :

• Closure of the set F is the set of all functional dependencies that can be inferred given the set F.




• Clearly F⁺ contains all of the functional dependencies in F.

Boyce–Codd Normal Form

• A relation schema R is in BCNF with respect to a set F of functional dependencies if, for all functional dependencies in F⁺ of the form α → β, where α ⊆ R and β ⊆ R, at least one of the following holds:




1. α → β is a trivial functional dependency (that is, β ⊆ α).




2. α is a superkey for schema R




• A database design is in BCNF if each member of the set of relation schemas that constitutes the design is in BCNF.




• inst_dept (ID, name, salary, dept_name, building, budget)




• The functional dependency dept_name → budget holds on inst_dept, but dept_name is not a superkey (because, a department may have a number of different instructors).




• However, if it is decomposed into instructor(ID, name, dept_name, salary) and department(dept_name, building, budget).




• Then these two are in BCNF as all the non-trivial dependencies such as ID → name, dept_name, salary and dept_name → building, budget have superkeys on the left side of the arrow.

Rule for Decomposing into BCNF

• If a relation R is not in BCNF then there is at least one nontrivial functional dependency α → β such that α is not a superkey for R. We replace R in our design with two schemas:




1. (α ∪ β)




2. (R - (β - α))




3. In the case of inst_dept above, α = dept name, β = {building, budget},and inst_dept is replaced by :




1. (α ∪ β)=(dept name, building,budget)




2. (R − (β − α)) = (ID, name, dept name, salary)




4. When we decompose a schema that is not in BCNF, it may be that one or more of the resulting schemas are not in BCNF. In such cases, further decomposition is required, the eventual result of which is a set of BCNF schemas.

Third Normal Form

• A relation schema R is in Third Normal Form with respect to a set F of functional dependencies if, for all functional dependencies in F⁺ of the form α → β, where α ⊆ R and β ⊆ R, at least one of the following holds:




1. α → β is a trivial functional dependency (that is, β ⊆ α).




2. α is a superkey for schema R




3. Each attribute A in β - α is contained in a candidate key for R.




• BCNF is therefore a more restrictive normal form than is 3NF. So all relations in BCNF are also in 3NF.

Previous

Next