Logic and Bit Operations
Computers represent information using bits. A bit is a symbol with two possible values, namely, 0 (zero) and 1 (one).
we will use a 1 bit to represent true and a 0 bit to represent false. That is, 1 represents T (true), 0 represents F (false). A variable is called a Boolean variable if its value is either true or false.
Consequently, a Boolean variable can be represented using a bit.
We will also use the notation OR, AND, and XOR for the operators ∨, ∧, and ⊕, as is done in various programming languages.
Table for the Bit Operators OR, AND, and XOR.
| x | y | x ∨ y | x ∧ y | x ⊕ y |
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 0 | 1 |
| 1 | 0 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 | 0 |
Q. Find the bitwise OR, bitwise AND, and bitwise XOR of the bit strings 01 1011 0110 and 11 0001 1101.
The bitwise OR, bitwise AND, and bitwise XOR of these strings are obtained by taking the OR, AND, and XOR of the corresponding bits, respectively
01 1011 0110 11 0001 1101 ------------ 11 1011 1111 bitwise OR 01 0001 0100 bitwise AND 10 1010 1011 bitwise XOR
Translating English Sentences
Q. How can this English sentence be translated into a logical expression? “You can access the Internet from campus only if you are a computer science major or you are not a freshman.”
we let a, c, and f represent “You can access the Internet from campus,” “You are a computer science major,” and “You are a freshman,” respectively
“only if” is one way a conditional statement can be expressed, this sentence can be represented as :
a → (c ∨ ¬f)
Q. How can this English sentence be translated into a logical expression? “You cannot ride the roller coaster if you are under 4 feet tall unless you are older than 16 years old.”
Let q, r, and s represent “You can ride the roller coaster,” “You are under 4 feet tall,” and “You are older than 16 years old,” respectively. Then the sentence can be translated to
(r ∧¬s) → ¬q.
Q. Express the specification “The automated reply cannot be sent when the file system is full” using logical connectives.
One way to translate this is to let p denote “The automated reply can be sent” and q denote “The file system is full.”
Then ¬p represents “It is not the case that the automated reply can be sent,” which can also be expressed as “The automated reply cannot be sent.” Consequently, our specification can be represented by the conditional statement q → ¬p.
Note : System specifications should be consistent, that is, they should not contain conflicting requirements that could be used to derive a contradiction. When specifications are not consistent, there would be no way to develop a system that satisfies all specifications.
Q. Determine whether these system specifications are consistent:
“The diagnostic message is stored in the buffer or it is retransmitted.”
“The diagnostic message is not stored in the buffer.”
“If the diagnostic message is stored in the buffer, then it is retransmitted.”
Let p denote “The diagnostic message is stored in the buffer” and let q denote “The diagnostic message is retransmitted.” The specifications can then be written as :
p ∨ q, ¬p, and p → q
An assignment of truth values that makes all three specifications true must have p false to make ¬p true.
Because we want p ∨ q to be true but p must be false, q must be true.
Because p → q is true when p is false and q is true, we conclude that these specifications are consistent, because they are all true when p is false and q is true.
Q. Determine whether these system specifications are consistent:
“The diagnostic message is stored in the buffer or it is retransmitted.”
“The diagnostic message is not stored in the buffer.”
“If the diagnostic message is stored in the buffer, then it is retransmitted.”
“The diagnostic message is not retransmitted”
The three specifications from above example are true only in the case when p is false and q is true. However, last specification is ¬q, which is false when q is true. Consequently, these four specifications are inconsistent.
Q. Smullyan posed many puzzles about an island that has two kinds of inhabitants, knights, who always tell the truth, and their opposites, knaves, who always lie. You encounter two people A and B. What are A and B if A says “B is a knight” and B says “The two of us are opposite types?
Let p and q be the statements that A is a knight and B is a knight, respectively, so that ¬p and ¬q are the statements that A is a knave and B is a knave, respectively.
consider the possibility that A is a knight; this is the statement that p is true. If A is a knight, then he is telling the truth when he says that B is a knight, so that q is true, and A and B are the same type.
However, if B is a knight, then B’s statement that A and B are of opposite types, the statement (p ∧¬q) ∨ (¬p ∧ q), would have to be true, which it is not, because A and B are both knights. Consequently, we can conclude that A is not a knight, that is, that p is false.
If A is a knave, then because everything a knave says is false, A’s statement that B is a knight, that is, that q is true, is a lie. This means that q is false and B is also a knave.
Furthermore, if B is a knave, then B’s statement that A and B are opposite types is a lie, which is consistent with both A and B being knaves. We can conclude that both A and B are knaves.
Q. A father tells his two children, a boy and a girl, to play in their backyard without getting dirty. However, while playing, both children get mud on their foreheads. When the children stop playing, the father says “At least one of you has a muddy forehead,” and then asks the children to answer “Yes” or “No” to the question: “Do you know whether you have a muddy forehead?” The father asks this question twice. What will the children answer each time this question is asked, assuming that a child can see whether his or her sibling has a muddy forehead, but cannot see his or her own forehead? Assume that both children are honest and that the children answer each question simultaneously
Let s be the statement that the son has a muddy forehead and let d be the statement that the daughter has a muddy forehead.
When the father says that at least one of the two children has a muddy forehead, he is stating that the disjunction s ∨ d is true.
Both children will answer “No” the first time the question is asked because each sees mud on the other child’s forehead. That is, the son knows that d is true, but does not know whether s is true, and the daughter knows that s is true, but does not know whether d is true.
After the son has answered “No” to the first question, the daughter can determine that d must be true. This follows because when the first question is asked, the son knows that s ∨ d is true, but cannot determine whether s is true
Using this information, the daughter can conclude that d must be true, for if d were false, the son could have reasoned that because s ∨ d is true, then s must be true, and he would have answered “Yes” to the first question.
The son can reason in a similar way to determine that s must be true. It follows that both children answer “Yes” the second time the question is asked.
Logic Circuits
The inverter,or NOT gate, takes an input bit p, and produces as output ¬p.
The OR gate takes two input signals p and q, each a bit, and produces as output the signal p ∨ q.
The AND gate takes two input signals p and q, each a bit, and produces as output the signal p ∧ q.
Q. Determine the output for the combinatorial circuit in Figure
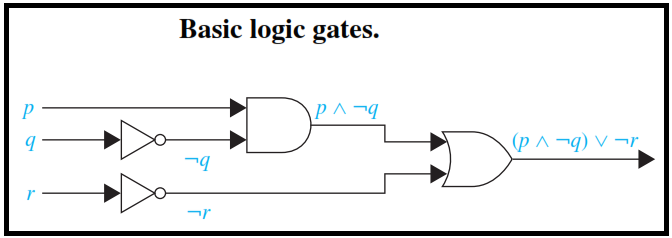
We see that the AND gate takes input of p and ¬q, the output of the inverter with input q, and produces p ∧¬q.
The OR gate takes input p ∧¬q and ¬r, the output of the inverter with input r, and produces the final output (p ∧¬q) ∨¬r.
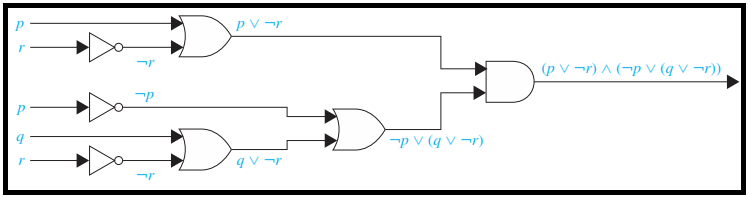
Q. Build a digital circuit that produces the output (p ∨ ¬r) ∧ (¬p ∨ (q ∨ ¬r)) when given input bits p, q, and r.
To construct the desired circuit, we build separate circuits for p ∨ ¬r and for ¬p ∨ (q ∨ ¬r) and combine them using an AND gate.
To construct a circuit for p ∨ ¬r, we use an inverter to produce ¬r from the input r.
Then, we use an OR gate to combine p and ¬r.To build a circuit for ¬p ∨ (q ∨¬r), we first use an inverter to obtain ¬r. Then we use an OR gate with inputs q and ¬r to obtain q ∨¬r.
Finally, we use another inverter and an OR gate to get ¬p ∨ (q ∨ ¬r) from the inputs p and q ∨ ¬r. To complete the construction, we employ a final AND gate, with inputs p ∨ ¬r and ¬p ∨ (q ∨¬r).
Propositional Equivalences
Tautology
A compound proposition that is always true, no matter what the truth values of the propositional variables that occur in it, is called a tautology.
A compound proposition that is always false is called a contradiction.
A compound proposition that is neither a tautology nor a contradiction is called a contingency.
Q. Construct examples of tautologies and contradictions using just one propositional variable.
Examples of a Tautology and a Contradiction.
| p | ¬p | p ∨ ¬p | p ∧ ¬p |
|---|---|---|---|
| T | F | T | F |
| F | T | T | F |
Logical Equivalences
Compound propositions that have the same truth values in all possible cases are called logically equivalent.
The compound propositions p and q are called logically equivalent if p ↔ q is a tautology.
The notation p ≡ q denotes that p and q are logically equivalent.
Examples of a Tautology and a Contradiction.
| p | ¬p | p ∨ ¬p | p ∧ ¬p |
|---|---|---|---|
| T | F | T | F |
| F | T | T | F |
Q. Show that ¬(p ∨ q) and ¬p ∧ ¬q are logically equivalent.
De Morgan’s Laws.
¬(p ∧ q) ≡ ¬p ∨ ¬q
¬(p ∨ q) ≡ ¬p ∧ ¬q
The truth tables for these compound propositions are displayed below.
Because the truth values of the compound propositions ¬(p ∨ q) and ¬p ∧¬q agree for all possible combinations of the truth values of p and q, it follows that ¬(p ∨ q) ↔ (¬p ∧¬q) is a tautology and that these compound propositions are logically equivalent.
Truth Tables for ¬(p ∨ q) and ¬p ∧¬q.
| p | q | p ∨ q | ¬(p ∨ q) | ¬p | ¬q | ¬p ∧¬q |
|---|---|---|---|---|---|---|
| T | T | T | F | F | F | F |
| T | F | T | F | F | T | F |
| F | T | T | F | T | F | F |
| F | F | F | T | T | T | T |
NOTE : 2n rows are required if a compound proposition involves 'n' propositional variables
Logical Equivalences
| Equivalence | Name |
|---|---|
| p ∧ T ≡ p ; p ∨ F ≡ p | Identity laws |
| p ∨ T ≡ T ; p ∧ F ≡ F | Domination laws |
| p ∨ p ≡ p ; p ∧ p ≡ p | Idempotent laws |
| ¬(¬p) ≡ p | Double negation law |
| p ∨ q ≡ q ∨ p ; p ∧ q ≡ q ∧ p | Commutative laws |
| (p ∨ q) ∨ r ≡ p ∨ (q ∨ r) ; (p ∧ q) ∧ r ≡ p ∧ (q ∧ r) | Associative laws |
| p ∨ (q ∧ r) ≡ (p ∨ q) ∧ (p ∨ r) ; p ∧ (q ∨ r) ≡ (p ∧ q) ∨ (p ∧ r) | Distributive laws |
| ¬(p ∧ q) ≡ ¬p ∨ ¬q ; ¬(p ∨ q) ≡ ¬p ∧ ¬q | De Morgan’s laws |
| p ∨ (p ∧ q) ≡ p ; p ∧ (p ∨ q) ≡ p | Absorption laws |
| p ∨ ¬p ≡ T ; p ∧ ¬p ≡ F | Negation laws |
Logical Equivalences Involving Conditional Statements.
p → q ≡ ¬p ∨ q
p → q ≡ ¬q → ¬p
p ∨ q ≡ ¬p → q
p ∧ q ≡ ¬(p → ¬q)
¬(p → q) ≡ p ∧ ¬q
(p → q) ∧ (p → r) ≡ p → (q ∧ r)
(p → r) ∧ (q → r) ≡ (p ∨ q) → r
(p → q) ∨ (p → r) ≡ p → (q ∨ r)
(p → r) ∨ (q → r) ≡ (p ∧ q) → r
Logical Equivalences Involving Biconditional Statements.
p ↔ q ≡ (p → q) ∧ (q → p)
p ↔ q ≡ ¬p ↔ ¬q
p ↔ q ≡ (p ∧ q) ∨ (¬p ∧ ¬q)
¬(p ↔ q) ≡ p ↔ ¬q
Use De Morgan’s laws to express the negations of “Miguel has a cellphone and he has a laptop computer” and “Heather will go to the concert or Steve will go to the concert.”
Let p be “Miguel has a cellphone” and q be “Miguel has a laptop computer.” Then “Miguel has a cellphone and he has a laptop computer” can be represented by p ∧ q.
By the first of De Morgan’s laws, ¬(p ∧ q) is equivalent to ¬p ∨ ¬q. Consequently, we can express the negation of our original statement as “Miguel does not have a cellphone or he does not have a laptop computer.”
Let r be “Heather will go to the concert” and s be “Steve will go to the concert.” Then “Heather will go to the concert or Steve will go to the concert” can be represented by r ∨ s.
By the second of De Morgan’s laws, ¬(r ∨ s) is equivalent to ¬r ∧ ¬s. Consequently, we can express the negation of our original statement as “Heather will not go to the concert and Steve will not go to the concert.”