Connectivity
Path or walk is a sequence of edges that begins at a vertex of a graph and travels from vertex to vertex along edges of the graph.
The path is a circuit or closed walk if it begins and ends at the same vertex. A path or circuit is simple if it does not contain the same edge more than once. A path or circuit is simple or sometimes called a trail if it does not contain the same edge more than once.
Some books use terminology path for a trail with no repeated vertices
An undirected graph is called connected if there is a path between every pair of distinct vertices of the graph. An undirected graph that is not connected is called disconnected. There is a simple path between every pair of distinct vertices of a connected undirected graph
A connected component of a graph G is a connected subgraph of G that is not a proper subgraph of another connected subgraph of G. That is, a connected component of a graph G is a maximal connected subgraph of G.
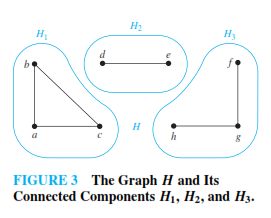
A graph G that is not connected has two or more connected components that are disjoint and have G as their union. The connected components of the graph H are shown below :
Sometimes the removal from a graph of a vertex and all incident edges produces a subgraph with more connected components. Such vertices are called cut vertices (or articulation points). The removal of a cut vertex from a connected graph produces a subgraph that is not connected. Analogously, an edge whose removal produces a graph with more connected components than in the original graph is called a cut edge or bridge. Every connected graph, except a complete graph, has a vertex cut.
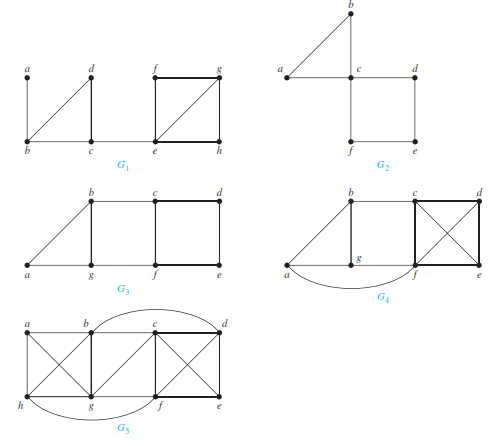
Q. ind the cut vertices and cut edges in the graph G1 shown below
The cut vertices of G1 are b, c, and e. The removal of one of these vertices (and its adjacent edges) disconnects the graph.
The cut edges are {a, b} and {c, e}.
Removing either one of these edges disconnects G1.
Euler Paths and Circuits
An Euler circuit in a graph G is a simple circuit containing every edge of G. An Euler path in G is a simple path containing every edge of G.
If a connected graph has an Euler circuit, then every vertex must have even degree.
A connected multigraph with at least two vertices has an Euler circuit if and only if each of its vertices has even degree.
A connected multigraph has an Euler path but not an Euler circuit if and only if it has exactly two vertices of odd degree.
A simple path in a graph G that passes through every vertex exactly once is called a Hamilton path, and a simple circuit in a graph G that passes through every vertex exactly once is called a Hamilton circuit.
A graph with a vertex of degree one cannot have a Hamilton circuit, because in a Hamilton circuit, each vertex is incident with two edges in the circuit.
Adding edges (but not vertices) to a graph with a Hamilton circuit produces a graph with the same Hamilton circuit.
A Hamilton circuit cannot contain a smaller circuit within it.
If G is a simple graph with n vertices with n ≥ 3 such that the degree of every vertex in G is at least n/2, then G has a Hamilton circuit.
If G is a simple graph with n vertices with n ≥ 3 such that deg(u) + deg(v) ≥ n for every pair of nonadjacent vertices u and v in G, then G has a Hamilton circuit
Planar Graphs
A graph is called planar if it can be drawn in the plane without any edges crossing (where a crossing of edges is the intersection of the lines or arcs representing them at a point other than their common endpoint). Such a drawing is called a planar representation of the graph.
All planar representations of a graph split the plane into the same number of regions.
Let G be a connected planar simple graph with e edges and v vertices. Let r be the number of regions in a planar representation of G. Then r = e − v + 2.
Q. Suppose that a connected planar simple graph has 20 vertices, each of degree 3. Into how many regions does a representation of this planar graph split the plane?
This graph has 20 vertices, each of degree 3, so v = 20. Because the sum of the degrees of the vertices, 3v = 3 · 20 = 60, is equal to twice the number of edges, 2e,wehave2e = 60, or e = 30. Consequently, from Euler’s formula, the number of regions is
r = e − v + 2 = 30 − 20 + 2 = 12.
Theories of Planar Graphs
If G is a connected planar simple graph with e edges and v vertices, where v ≥ 3, then e ≤ 3v − 6.
If G is a connected planar simple graph, then G has a vertex of degree not exceeding five.
If a connected planar simple graph has e edges and v vertices with v ≥ 3 and no circuits of length three, then e ≤ 2v − 4.
Graph Coloring
A coloring of a simple graph is the assignment of a color to each vertex of the graph so that no two adjacent vertices are assigned the same color.
The chromatic number of a graph is the least number of colors needed for a coloring of this graph. The chromatic number of a graph G is denoted by χ(G). (Here χ is the Greek letter chi.)
THE FOUR COLOR THEOREM : The chromatic number of a planar graph is no greater than four.
Q. Scheduling Final Exams: How can the final exams at a university be scheduled so that no student has two exams at the same time?
This scheduling problem can be solved using a graph model, with vertices representing courses and with an edge between two vertices if there is a common student in the courses they represent. Each time slot for a final exam is represented by a different color. A scheduling of the exams corresponds to a coloring of the associated graph.
For instance, suppose there are seven finals to be scheduled. Suppose the courses are numbered 1 through 7. Suppose that the following pairs of courses have common students: 1 and 2, 1 and 3, 1 and 4, 1 and 7, 2 and 3, 2 and 4, 2 and 5, 2 and 7, 3 and 4, 3 and 6, 3 and 7, 4 and 5, 4 and 6, 5 and 6, 5 and 7, and 6 and 7. In Figure 8 the graph associated with this set of classes is shown. A scheduling consists of a coloring of this graph.
Because the chromatic number of this graph is 4 (the reader should verify this), four time slots are needed.