Synchronization

• A cooperating process is one that can affect or be affected by other processes executing in the system. Cooperating processes can either directly share a logical address space (that is, both code and data) or be allowed to share data only through files or messages.




• Concurrent access to shared data may result in data inconsistency but there are various mechanisms to ensure the orderly execution of cooperating processes that share a logical address space, so that data consistency is maintained.

Producer Consumer problem

• The code for the producer process is as follows:




1. while (true) {
         /* produce an item in next Produced */
         while (counter == BUFFER_SIZE)
           ; /* do nothing */ 
         buffer[in] = nextProduced;
         in = (in + 1) % BUFFER_SIZE ; 
         counter++; 
   }




• The code for the consumer process is as follows:




1. while (true) { 
         while (counter == 0) 
            ; /* do nothing */ 
         nextConsumed = buffer[out];
         out = (out + 1) % BUFFER_SIZE; 
         counter--; 
   /* consume the item in nextConsumed */
   }




• Suppose that the value of the variable counter is currently 5 and that the producer and consumer processes execute the statements "counter++" and "counter--" concurrently.




• Following the execution of these two statements, the value of the variable counter may be 4, 5, or 6 when it should be 5.




• We would arrive at this incorrect state because we allowed both processes to manipulate the variable counter concurrently.




• A situation like this, where several processes access and manipulate the same data concurrently and the outcome of the execution depends on the particular order in which the access takes place, is called a "Race Condition".




• To ensure that this doesn't occur we need "process synchronization".

Critical Section

• Each process has a segment of code, called a "critical section" in which the process may be changing common variables, updating a table, writing a file, and so on.




• When one process is executing in its critical section no other process is to be allowed to execute in its critical section.




• No two processes are executing in their critical sections at the same time. The "critical-section problem" is to design a protocol that the processes can use to cooperate. Each process must request permission to enter its critical section.




• The section of code implementing this request is the "Entry section". The critical section may be followed by an "exit section". The remaining code is the "remainder section".

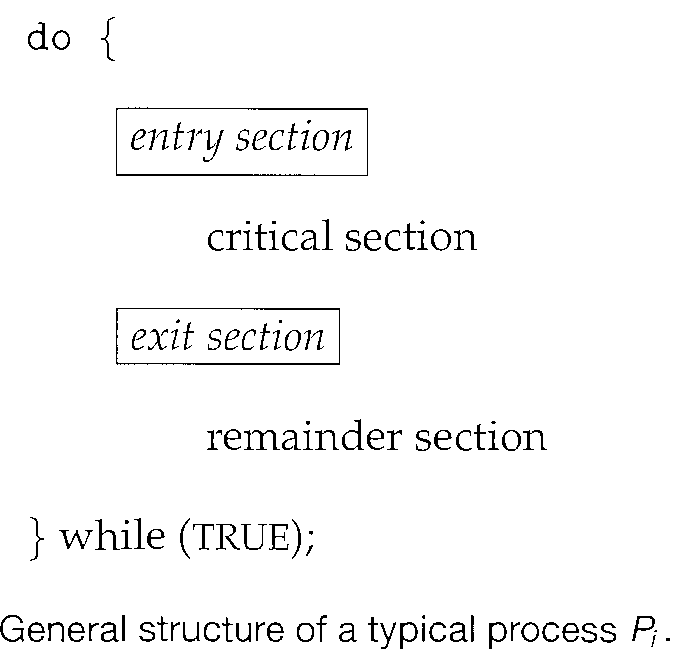
A solution to the critical-section problem

• Mutual exclusion. If process P_i is executing in its critical section, then no other processes can be executing in their critical sections.




• Progress. If no process is executing in its critical section and some processes wish to enter their critical sections, then only those processes that are not executing in their remainder sections can participate in deciding which will enter its critical section next, and this selection cannot be postponed indefinitely.




• Bounded waiting. There exists a bound, or limit, on the number of times that other processes are allowed to enter their critical sections after a process has made a request to enter its critical section and before that request is granted.

General approaches are used to handle critical sections in operating systems:

• Two general approaches are used to handle critical sections in operating systems: (1) preemptive kernels and (2) non-preemptive kernels.




• A preemptive kernel allows a process to be preempted while it is running in kernel mode.




• A non-preemptive kernel does not allow a process running in kernel mode to be preempted; a kernel-mode process will run until it exits kernel mode, blocks, or voluntarily yields control of the CPU.

Peterson's solution

• Peterson's solution is restricted to two processes that alternate execution between their critical sections and remainder sections. The processes are numbered P₀ and P₁.




• Peterson's solution requires the two processes to share two data items:




1. int turn;
            boolean flag[2]; 




• The variable turn indicates whose turn it is to enter its critical section. That is, if turn == i, then process P_i is allowed to execute in its critical section.




• The flag array is used to indicate if a process is ready to enter its critical section. For example, if flag [i] is true, this value indicates that P_i is ready to enter its critical section.




• To enter the critical section, process Pi first sets flag [i] to be true and then sets turn to the value j, thereby asserting that if the other process wishes to enter the critical section, it can do so.




• If both processes try to enter at the same time, turn will be set to both i and j at roughly the sance time. Only one of these assignments will last; the other will occur but will be overwritten immediately.




• The structure of process P_i in Peterson's solution.




• do { 
      flag [i] = TRUE; 
      turn = j;
      while (flag[j] && turn == j); 
           critical section 
      flag [i] = FALSE; 
           remainder section
  } while (TRUE); 




• The eventual value of turn determines which of the two processes is allowed to enter its critical section first.

Proof of correctness of Peterson principle

• To prove that this solution is correct. It must be shown that: Mutual exclusion is preserved. The progress requirement is satisfied. The bounded-waiting requirement is met.




• Proof of Mutual exclusion




1. P_i enters its critical section only if either flag [j] == false or turn == i. Also note that, if both processes can be executing in their critical sections at the same time, then flag [0] == flag [1] == true




2. These two observations imply that P₀ and P₁ could not have successfully executed their while statements at about the same time, since the value of turn can be either 0 or 1 but can't be both.




3. Hence, one of the processes -say, P_i - must have successfully executed the while statement, whereas P; had to execute at least one additional statement ("turn == j").




4. However, at that time, flag [j] == true and turn == j, and this condition will persist as long as P_j is in its critical section; as a result, mutual exclusion is preserved.




• Proof of progress requirement and bounded-waiting :




1. P_i can be prevented from entering the critical section only if it is stuck in the while loop with the condition flag [j] == true and turn == j; this loop is the only one possible.




2. If P_j is not ready to enter the critical section, then flag [j] == false, and P_i can enter its critical section.




3. If P_j has set flag [j] to true and is also executing in its while statement, then either turn == i or turn == j.




4. If turn == i, then P_j will enter the critical section. If turn == j, then P_i will enter the critical section. However, once P_i exits its critical section, it will reset flag [j] to false, allowing P_j to enter its critical section.




5. If P_j resets flag [j] to true, it must also set turn to i. Thus, since P_i does not change the value of the variable turn while executing the while statement, P_i will enter the critical section (progress) after at most one entry by P_j (bounded waiting).

Semaphore

• A semaphore "S" is an integer variable that, apart from initialization, is accessed only through two standard atomic operations: wait () and signal ().




• The wait () operation was originally termed P (from the Dutch - proberen, "to test"); signal() was originally called V (from verhogen, "to increment").




• The definition of wait () is as follows:




1. wait(S) { 
   } 
   while S <= 0 
   ; //  no-op
   s--;
   }
   




• The definition of signal() is as follows:




1. signal(S) { 
   S++; 
   } 
   




• All modifications to the integer value of the semaphore in the wait () and signal() operations must be executed indivisibly.




• That is, when one process modifies the semaphore value, no other process can simultaneously modify that same semaphore value.




• In addition, in the case of wait (S), the testing of the integer value of S (S ≤ 0), as well as its possible modification (S--), must be executed without interruption.




• Operating systems often distinguish between counting and binary semaphores. The value of a counting semaphore can range over an unrestricted domain. The value of a binary semaphore i.e. mutex locks, as they are locks that provide mutual exclusion, can range only between 0 and 1.




• Counting semaphores can be used to control access to a given resource consisting of a finite number o£ instances. The semaphore is initialized to the number of resources available.




• Each process that wishes to use a resource performs a wait() operation on the semaphore (thereby decrementing the count). When a process releases a resource, it performs a signal() operation (incrementing the count).




• When the count for the semaphore goes to 0, all resources are being used. After that, processes that wish to use a resource will block until the count becomes greater than 0.

Disadvantage of the semaphore

• While a process is in its critical section, any other process that tries to enter its critical section must loop continuously in the entry code. This continual looping is clearly a problem in a real multi - programming system where a single CPU is shared among many processes. This is called "Busy Waiting".




• Busy waiting wastes CPU cycles that some other process might be able to use productively. This type of semaphore is also called a "Spinlock" because the process "spins" while waiting for the lock.




• To overcome the need for busy waiting, we can modify the definition of the wait() and signal() semaphore operations. When a process executes the wait () operation and finds that the semaphore value is not positive, it must wait. However, rather than engaging in busy waiting, the process can block itself.




• The block operation places a process into a waiting queue associated with the semaphore, and the state of the process is switched to the waiting state. Then control is transferred to the CPU scheduler, which selects another process to execute.

Deadlocks and Starvation

• we consider a system consisting of two processes, P₀ and P₁ , each accessing two semaphores, S and Q, set to the value 1:




• P0          P1
  wait(S);   wait(Q);
  wait(Q);   wait(Q);
  .
  .
  .
  signal(S);  signal(Q);
  signal(Q);  signal(S);
  




• Suppose that P₀ executes wait (S) and then P₁ executes wait (Q). When P₀ executes wait (Q), it must wait until P₁ executes signal (Q). Similarly, when P₁ executes wait (S), it must wait until P₀ executes signal(S). Since these signal() operations cannot be executed, P₀ and P₁ are deadlocked.

Priority Inversion and Priority Inheritance

• Assume we have three processes, Lf M, and H, whose priorities follow the order L < M < H. Assume that process H requires resource R, which is currently being accessed by process L. Ordinarily, process H would wait for L to finish using resource R.




• However, now suppose that process M becomes runnable, thereby preempting process L.




• Indirectly, a process with a lower priority-process M-has affected how long process H must wait for L to relinquish resource R.




• This problem is known as "Priority Inversion". It occurs only in systems with more than two priorities, so one solution is to have only two priorities. That is insufficient for most general-purpose operating systems. To solve we use a technique "priority Inheritance".




• Here all processes that are accessing resources needed by a higher-priority process inherit the higher priority until they are finished with the resources in question. When they are finished, their priorities revert to their original values.




• In the exan1.ple above, a priority-inheritance protocol would allow process L to temporarily inherit the priority of process H, thereby preventing process M from preempting its execution.




• When process L had finished using resource R, it would relinquish its inherited priority from Hand assume its original priority. Because resource R would now be available, process H-not M-would run next.

Previous

Next