Deadlock-avoidance approach
Given apriori information, it is possible to construct an algorithm that ensures that the system will never enter a deadlocked state. Such an algorithm defines the deadlock-avoidance approach. A deadlock-avoidance algorithm dynamically examines the resource-allocation state to ensure that a circular wait condition can never exist.
The resource-allocation state is defined by the number of available and allocated resources and the maximum demands of the processes.
For example, in a system with one tape drive and one printer, the system might need to know that process "P" will request first the tape drive and then the printer before releasing both resources, whereas process "Q" will request first the printer and then the tape drive. With this knowledge of the complete sequence of requests and releases for each process, the system can decide for each request whether or not the process should wait in order to avoid a possible future deadlock.
Q. What is a safe state ?
A state is safe if the system can allocate resources to each process (up to its maximum) in some order and still avoid a deadlock.
A sequence of processes > P1, P2 , ... , Pn < is a safe sequence for the current allocation state if, for each Pi , the resource requests that Pi can still make can be satisfied by the currently available resources plus the resources held by all Pj, with j < i.
In this situation, if the resources that Pi needs are not immediately available, then Pi can wait until all Pj have finished. When they have finished, Pi can obtain all of its needed resources, complete its designated task, return its allocated resources, and terminate.
If no such sequence exists, then the system state is said to be unsafe.
A safe state is not a deadlocked state. Conversely, a deadlocked state is an unsafe state. Not all unsafe states are deadlocks. An unsafe state may lead to a deadlock. As long as the state is safe, the operating system can avoid unsafe (and deadlocked) states.
In an unsafe state, the operating system cannot prevent processes from requesting resources in such a way that a deadlock occurs.
Resource-Allocation-Graph Algorithm - Deadlock-avoidance approach
In addition to the request and assignment edges in a Resource-Allocation-Graph we introduce a new type of edge, called a claim edge.
A claim edge Pi -> Rj indicates that process Pi may request resource Rj at some time in the future. This edge resembles a request edge in direction but is represented in the graph by a dashed line.
When a request is actually made, a claim edge becomes a request edge. Also, when a resource is released by a process its assignment edge is reconverted to a claim edge.
Resources must be claimed a priori in this system.
If a process Pi requests resource Rj. The request can be granted only if converting the request edge Pi -> Rj to an assignment edge Rj -> Pi does not result in the formation of a cycle in the resource-allocation graph.
We check for safety by using a cycle-detection algorithm. An algorithm for detecting a cycle in this graph requires an order of n2 operations, where "n" is the number of processes in the system.
If no cycle exists, then the allocation of the resource will leave the system in a safe state. If a cycle is found, then the allocation will put the system in an unsafe state.
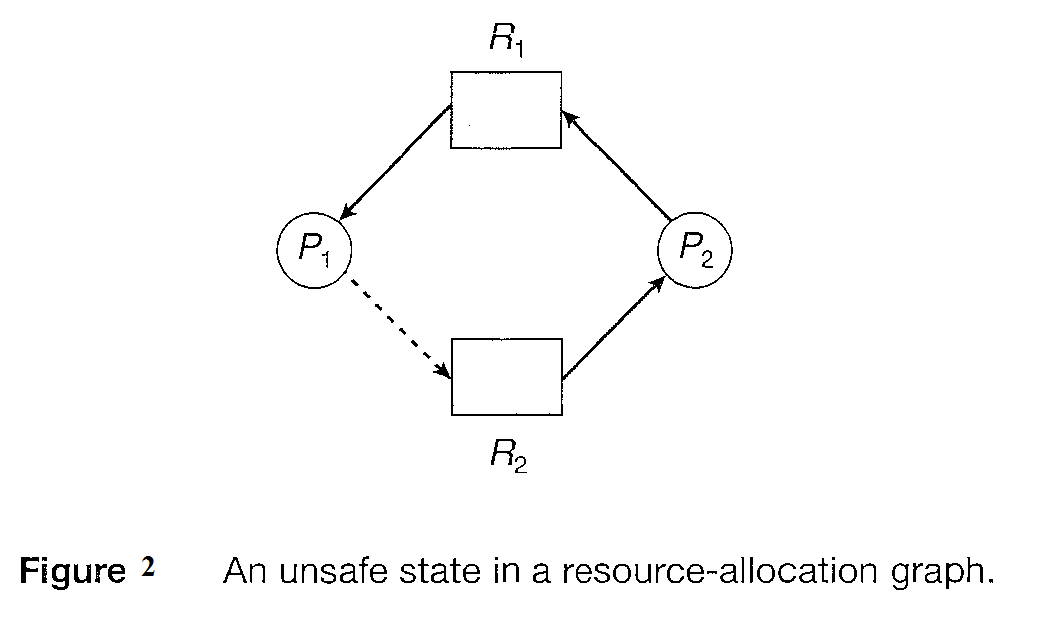
For the Figure 2 will deadlocks occur ?
In Figure 2, If P 1 requests R 2 then a deadlock will occur.
Banker's Algorithm - Deadlock-avoidance approach
The resource-allocation-graph algorithm is not applicable to a resource allocation system with multiple instances of each resource type.
Step 1 : When a new process enters the system, it must declare the maximum number of instances of each resource type that it may need. This nun1.ber may not exceed the total number of resources in the system.
Step 2: When a user requests a set of resources, the system must determine whether the allocation of these resources will leave the system in a safe state. If it will, the resources are allocated; otherwise, the process must wait until some other process releases enough resources.
Q. Data Structures needed for the bankers algorithm ?
We need the following data structures, "n" is the number of processes in the system and "m" is the number of resource types:
Available. A vector of length "m" indicates the number of available resources of each type. If Available[j] equals k, then k instances of resource type Rj are available.
Max. An n x m matrix defines the maximum demand of each process. If Max[i] [j] equals k, then process Pi may request at most k instances of resource type Rj.
Allocation. An n x m matrix defines the number of resources of each type currently allocated to each process. If Allocation[i][j] equals k, then process Pi is currently allocated "k" instances of resource type Rj.
Need. An n x m matrix indicates the remaining resource need of each process. If Need[i][j] equals k, then process Pi may need k more instances of resource type Rj to complete its task. Note that Need[i][j] equals Max[i][j] - Allocation[i][j].
Q. Present the algorithm for finding out whether or not a system is in a safe state
Let Work and Finish be vectors of length "m" and "n", respectively. Initialize Work = Available and Finish[i] = false for i = 0, 1, ... , n - 1.
Find an index "i" such that both
Finish[i] == false Needi ≤ Work If no such i exists, go to step 4.
Work = Work + Allocation; Finish[i] = true Go to step 2.
If Finish[i] == true for all i, then the system is in a safe state
This algorithm may require an order of m x n2 operations to determine whether a state is safe.
Q. Describe the algorithm for determining whether requests can be safely granted.
Let Requesti be the request vector for process Pi. If Requesti[j] == k, then process Pi wants k instances of resource type Rj. When a request for resources is made by process Pi, the following actions are taken:
If Requesti ≤ Needi; go to step 2. Otherwise, raise an error condition, since the process has exceeded its maximum claim.
If Requesti ≤ Available, go to step 3. Otherwise, Pi must wait, since the resources are not available.
Have the system pretend to have allocated the requested resources to process Pi by modifying the state as follows:
Available = Available- Requesti; Allocationi = Allocationi +Requesti; Needi = Needi - Requesti;
If the resulting resource-allocation state is safe, the transaction is com pleted, and process Pi is allocated its resources. However, if the new state is unsafe, then Pi must wait for Requesti, and the old resource - allocation state is restored.
Illustrate the use of the Banker's Algorithm
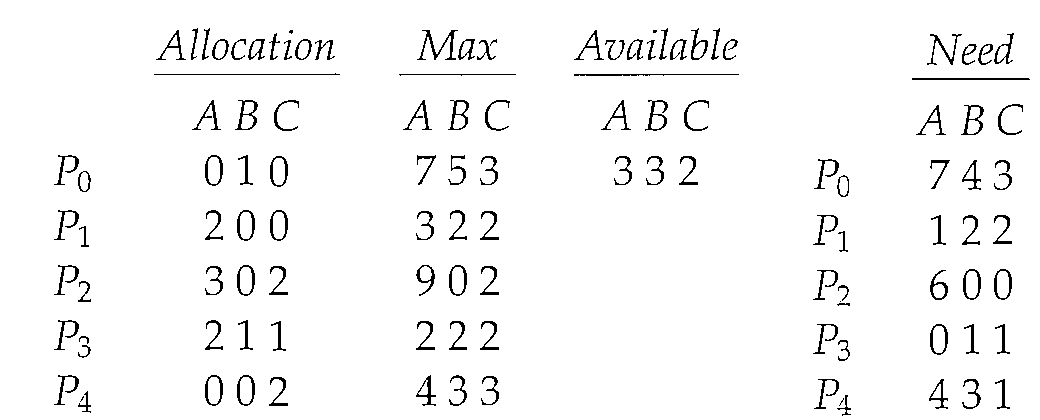
Consider a system with five processes P0 through P4 and three resource types A, B, and C. Resource type A has ten instances, resource type B has five instances, and resource type C has seven instances. At time T0, the following snapshot of the system has been taken:
The content of the matrix Need is defined to be Max - Allocation is also given above.
We claim that the system is currently in a safe state. Indeed, the sequence >P1, P3, P4, P2, P0< satisfies the safety criteria.
Suppose now that process P1 requests one additional instance of resource type A and two instances of resource type C, so Request1 = (1,0,2).
To decide whether this request can be immediately granted, we first check that Request1 is Available-that is, that (1,0,2) ≤ (3,3,2), which is true.
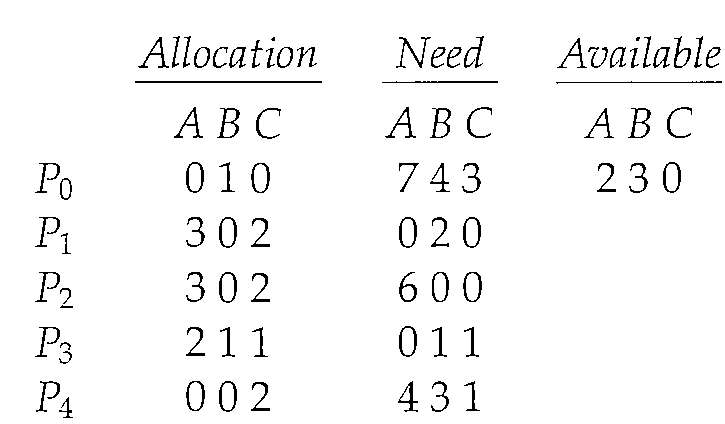
After this request has been fulfilled, and we arrive at the following new state:
We must determine whether this new system state is safe. To do so, we execute our safety algorithm and find that the sequence >P1, P3, P4, P2, P0< satisfies the safety requirement. Hence, we can immediately grant the request of process P1.
However, a request for (3,3,0) by P4 cannot be granted, since the resources are not available. Furthermore, a request for (0,2,0) by Po cannot be granted, even though the resources are available, since the resulting state is unsafe.
Deadlock Detection - Wait for Graph
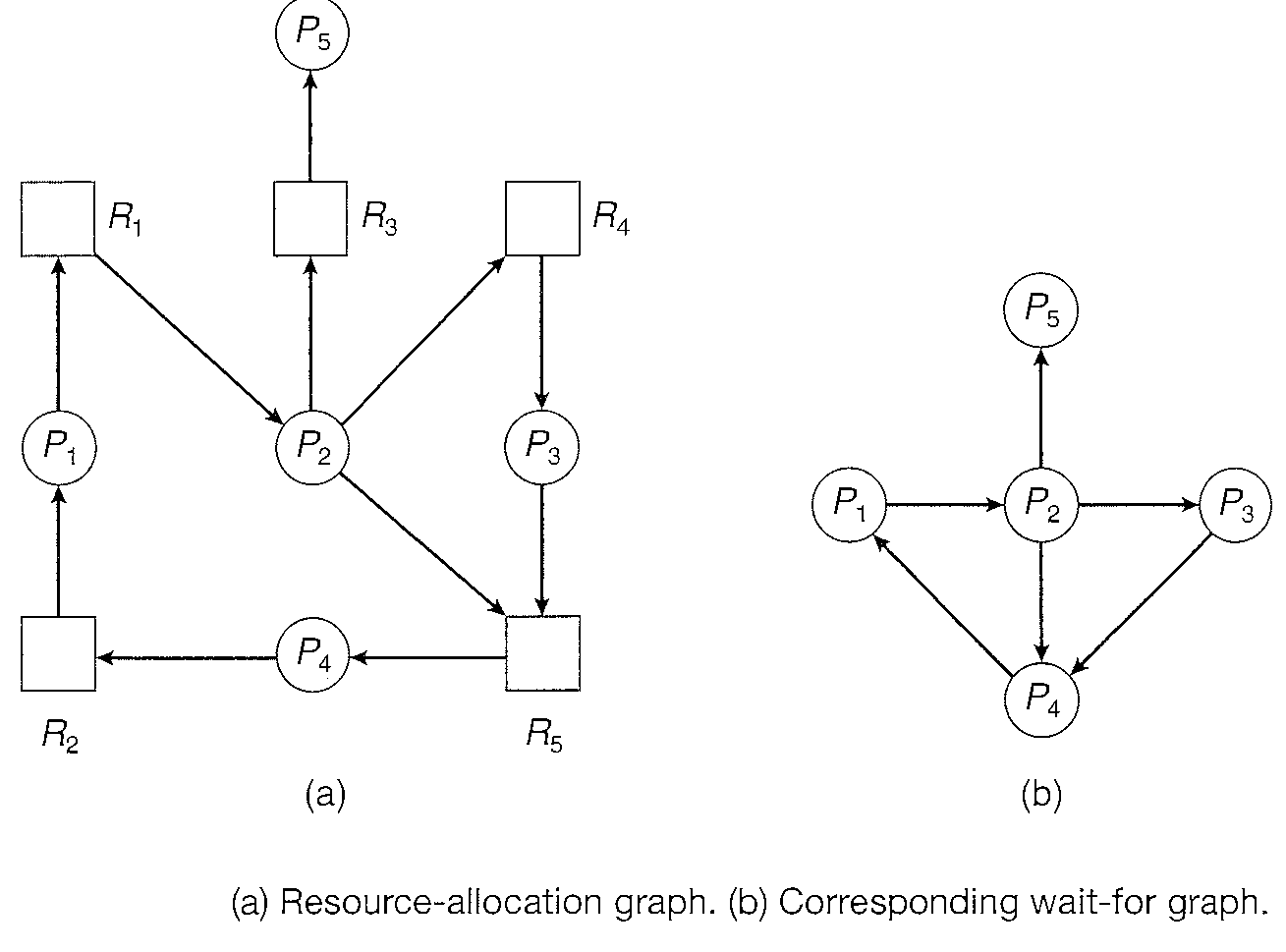
A deadlock detection algorithm uses a variant of the resource-allocation graph, called a wait-for graph.
an edge from Pi to Pj in a wait-for graph implies that process Pi is waiting for process Pj to release a resource that Pi needs.
An edge Pi -> Pj exists in a wait-for graph if and only if the corresponding resource allocation graph contains two edges Pi -> Rq and Rq -> Pj for some resource Rq.
A deadlock exists in the system if and only if the wait-for graph contains a cycle. To detect deadlocks, the system needs to maintain the wait-for graph and periodically invoke an algorithm that searches for a cycle in the graph.
An algorithm to detect a cycle in a graph requires an order of n2 operations, where "n" is the number of vertices in the graph.
Recovery from Deadlocks
There are two options for breaking a deadlock One is simply to abort one or more processes to break the circular wait. The other is to preempt some resources from one or more of the deadlocked processes.
Process Termination
Abort all deadlocked processes. This method clearly will break the deadlock cycle, but at great expense; the deadlocked processes may have computed for a long time, and the results of these partial computations must be discarded and probably will have to be recomputed later.
Abort one process at a time until the deadlock cycle is eliminated. This method incurs considerable overhead, since after each process is aborted, a deadlock-detection algorithm must be invoked to determine whether any processes are still deadlocked.
Aborting a process may not be easy. If the process was in the midst of updating a file, terminating it will leave that file in an incorrect state. Similarly, if the process was in the midst of printing data on a printer, the system must reset the printer to a correct state before printing the next job.
Resource Preemption : To eliminate deadlocks using resource preemption, we successively preempt some resources from processes and give these resources to other processes till the deadlock cycle is broken.
Selecting a victim. Which resources and which processes are to be preempted? As in process termination, we must determine the order of preemption to minimize cost. Cost factors may include such parameters as the number of resources a deadlocked process is holding and the amount of time the process has thus far consumed during its execution.
Rollback. If we preempt a resource from a process, what should be done with that process? Clearly, it cannot continue with its normal execution; it is missing some needed resource. We must roll back the process to some safe state and restart it from that state. Since, in general, it is difficult to determine what a safe state is, the simplest solution is a total rollback: abort the process and then restart it. Although it is more effective to roll back the process only as far as necessary to break the deadlock, this method requires the system to keep more information about the state of all running processes.
Starvation. In a system where victim selection is based primarily on cost factors, it may happen that the same process is always picked as a victim. As a result, this process never completes its designated task, a starvation situation that must be dealt with in any practical system. Clearly, we must ensure that a process can be picked as a victim" only a (small) finite number of times. The most common solution is to include the number of rollbacks in the cost factor.