Chapter-10: Straight Lines

 

Exercise – 10.1

Q-1. Construct a quadrilateral in the Cartesian plane with vertices (-2, 5), (0, 6), (4, -4) and (-3, -1). Also, find the area of the quadrilateral.

Solution. Based on formulae given in Straight Lines

Let, MNOP be the given quadrilateral having vertices M (-2, 5), N (0, 6), O (4, -4) and P (-3, -1).

Now, plot M, N, O and P on the Cartesian plane and join MN, NO, OP and PM.

The quadrilateral, thus, formed will be

 

As we need to find the area of the quadrilateral MNOP, so draw a diagonal, say, MO.

Now,

Area of (MNOP) = area of (\(\Delta MNO \)) + area of ( \( \Delta MOP \) )

Area of a triangle with vertices (a₁, b₁), (a₂, b₂), (a₃, b₃) and (a₄, b₄) is given by:

\(\frac{ 1 }{ 2 } \) | a₁ (b₂ – b₃ ) + a₂ (b₃ – b₁ ) + a₃ (b₁ – b₂ ) |

Now,

Vertices of \(\Delta MNO \) is M (-2, 5), N (0, 6) and O (4, -4)

Area of \(\Delta MNO \) = \(\frac{ 1 }{ 2 }\left | \left [ -2\left ( -6 – \left ( -4 \right ) \right ) + 0\left ( -4 – \left ( 5\right ) \right ) + 4\left ( 5 – \left ( 6 \right ) \right ) \right ] \right |\)

= \(\frac{ 1 }{ 2 }\left | \left [ -2\left ( -6 + 4 \right ) + 0\left ( -4 – 5 \right ) + 4\left ( 5 – 6 \right ) \right ] \right | \\ = \frac{ 1 }{ 2 }\left | \left [ -20 + 0 – 4 \right ] \right | \\ = \frac{ 1 }{ 2 }\left | -24 \right |\)

= \(\frac{ 1 }{ 2 } \times 24 \)

= 12 unit²

Vertices of \(\Delta MOP \) is M (-2, 5), O (4, -4) and P (-3, -1).

Area of \(\Delta MOP \) = \(\frac{ 1 }{ 2 }\left | \left [ -2\left ( -4 – \left ( -1 \right ) \right ) + 4\left ( -1 – \left ( 5\right ) \right ) – 3\left ( 5 – \left ( -4 \right ) \right ) \right ] \right |\)

= \(\frac{ 1 }{ 2 }\left | \left [ -2\left ( -4 + 1 \right ) + 4\left ( -1 – 5 \right ) – 3\left ( 5 + 4 \right ) \right ] \right | \\ = \frac{ 1 }{ 2 }\left | \left [ 6 – 24 – 27 \right ] \right | \\ = \frac{ 1 }{ 2 }\left | -45 \right |\)

= \(\frac{ 1 }{ 2 } \times 45 \)

= 22.5 unit²

Area of MNOP = Area of \(\Delta MNO \) + Area of \(\Delta MOP \)

= 12 + 22.5 = 34.5 22.5 unit²

 

Q-2. Consider an equilateral triangle, each of whose sides are 2b which lies on the y- axis in such a manner that, the mid- point of each of its base is at the origin. Obtain all the vertices of the equilateral triangle.

Solution. Based on formulae given in Straight Lines

Let, XYZ be the given equilateral triangle each of whose side is 2b.

Since, XYZ is an equilateral triangle,

So, XY = YZ = ZX = 2b

Now, consider that the base YZ lies along y-axis in such a way that it’s mid- point is at the origin.

So, YA = AZ = b, where A is the origin.

Thus, by our observation, the coordinates of the point Y are (0, b), while the coordinates of the point Z is (0, -a).

We know that, the line joining the vertex of an equilateral triangle having the mid- point of its opposite sides is perpendicular.

Thus, the vertex X lies on the y- axis.

 

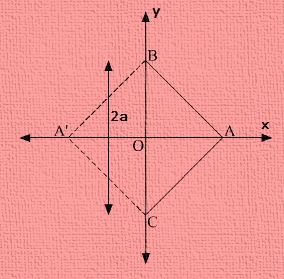
By applying the Pythagoras theorem to \(\Delta XAZ\), we will get

( XZ )² = ( AX )² + ( AZ )²

\(\Rightarrow \left ( 2b \right )^{ 2 } = \left ( AX \right )^{ 2 } + \left ( b \right )^{ 2 }\) \(\Rightarrow \left ( AX \right )^{ 2 } = \left ( 4b^{ 2 } – b^{ 2 } \right )\) \(\Rightarrow \left ( AX \right )^{ 2 } = 3b^{ 2 } \) \(\Rightarrow AX = \pm \sqrt{ 3 }b\)

The coordinate of the point X = ( \( \pm \sqrt{ 3 }b\) , 0 )

Hence, the vertices of the equilateral triangle XYZ are X( \( \sqrt{ 3 }b\) , 0 ), Y( 0, b ) and Z( 0, -b ) or X( \( -\sqrt{ 3 }b\) , 0 ), Y( 0, b ) and Z( 0, -b )

 

Q-3. What is the distance between X (a₁, b₁) and Y (a₂, b₂) if:

(a) XY is parallel to x- axis

(b) XY is parallel to y- axis

Solution. Based on formulae given in Straight Lines

Given points are X (a₁, b₁) and Y (a₂, b₂)

(a) The given condition is:

XY is parallel to the x- axis, i.e., b₁ = b₂

Therefore, the distance hence measured between X and Y in this case = \(\sqrt{ \left ( a_{ 2 } – a_{ 1 } \right )^{ 2 } + \left ( b_{ 2 } – b_{ 1 } \right )^{ 2 } }\)

= \(\sqrt{ \left ( a_{ 2 } – a_{ 1 } \right )^{ 2 } + \left ( b_{ 2 } – b_{ 2 } \right )^{ 2 } }\)

= \(\sqrt{ \left ( a_{ 2 } – a_{ 1 } \right )^{ 2 } }\)

= | a_{2 –} a₁ |

(b) The given condition is:

XY is parallel to the y- axis, i.e., a₁ = a₂

Therefore, the distance hence measured between X and Y in this case = \(\sqrt{ \left ( a_{ 2 } – a_{ 1 } \right )^{ 2 } + \left ( b_{ 2 } – b_{ 1 } \right )^{ 2 } }\)

= \(\sqrt{ \left ( a_{ 2 } – a_{ 2 } \right )^{ 2 } + \left ( b_{ 2 } – b_{ 1 } \right )^{ 2 } }\)

= \(\sqrt{ \left ( b_{ 2 } – b_{ 1 } \right )^{ 2 } }\)

= | b_{2 –} b₁ |

 

Q-4. Consider two points (6, 5) and (4, 2). Get a point on the y- axis which is equivalent from the given two points.

Solution. Based on formulae given in Straight Lines

Let us assume that, (0, y) be the given point on y- axis which is equivalent to the two given points (6, 5) and (4, 2).

Now,

\(\sqrt{ \left ( 6 – 0 \right )^{ 2 } + \left ( 5 – a \right )^{ 2 }} = \sqrt{ \left ( 4 – 0 \right )^{ 2 } + \left ( 2 – a \right )^{ 2 }}\) \(\Rightarrow \sqrt{ 36 + 25 – 10a + a^{ 2 }} = \Rightarrow \sqrt{ 16 + 4 – 4a + a^{ 2 }}\) \(\Rightarrow \sqrt{ 41 } = \sqrt{ 6a }\)

Squaring both side, we will get

6a = 41

a = \(\frac{ 41 }{ 6 }\)

a = 6.8 unit

Therefore, (0, \(\frac{ 41 }{ 6 }\) ) is the point on Y – axis which is equivalent to the given points (6, 5) and (4, 2).

 

Q-5. What is the slope of a line passing through the origin and, the mid- point of the line- segment joining the two points O (0, -5) and A (9, 0)?

Solution. Based on formulae given in Straight Lines

The two points of the line- segment is O (0, -5) and A (9, 0).

Then, the co-ordinates of the mid-point of line-segment OA are-

\(\left( \frac{ 0 + 9 }{ 2 } , \frac{ -5 + 0 }{ 2 } \right )\) = ( 4.5, -2.5 )

We know that the slope (say, m) of the non- vertical line which passes through the points (a₁, b₁) and (a₂, b₂) is:

m = \(\frac{ b_{1} – b_{2} }{ a_{1} – a_{2} }\), a₂ ≠ a₁

Hence, the slope of the line- segment passing through (0, 0) and (4.5, -2.5) is given by:

\(\frac{ -2.5 – 0 }{ 4.5 – 0 } = \frac{ -2.5 }{ 4.5 } = \frac{ -25 }{ 45 } = \frac{ -5 }{ 9 }\)

Therefore, the required slope of the line-segment = \( \frac{ -5 }{ 9 }\)

 

Q-6. Prove that the points (5, 5), (4, 6) and (-2, -2) are the vertices of the right- angled triangle, without using Pythagoras theorem.

Solution. Based on formulae given in Straight Lines

There are three points given in the question. Let, those points be the vertices of the triangle XYZ, namely, X (5, 5), Y (4, 6) and Z (-2, -2).

We know that, the slope (say, m) of the non- vertical line which passes through the points (a₁, b₁) and (a₂, b₂) is:

m = \(\frac{ b_{1} – b_{2} }{ a_{1} – a_{2} }\), a₂ ≠ a₁

The slope of XY( m₁ ) = \(\frac{ 6 – 5 }{ 4 – 5 }\) = -1.

The slope of YZ( m₂ ) = \(\frac{ -2 – 6 }{ -2 – 4} = \frac{ -8 }{ -6 } = \frac{ 4 }{ 3 }\)

The slope of ZX( m₃ ) = \(\frac{ 5 + 2 }{ 5 + 2 } = \frac{ 7 }{ 7 } = 1\)

Here, we can see that, m₁. m₃ = -1

This proves that, the line- segments XY and ZX is perpendicular to each other, i.e., the triangle XYZ is right- angled at X (5, 5).

Hence, proved that the given points, i.e., (5, 5), (4, 6) and (-2, -2) are the vertices of the right- angled triangle.

Q-7. What is the slope of the line which makes an angle \(60^{\circ}\) along the positive direction of the Y- axis which is measured in anticlockwise sequence.

Solution. Based on formulae given in Straight Lines

By mathematical calculation rule,

If a line makes an angle of \(60^{\circ}\) with any of the positive direction of the axis which is measured in an anticlockwise sequence, then the angle made by the line with positive direction of the corresponding axis is also measured in anticlockwise sequence is given by,

\( 90^{\circ} + x^{\circ}\).

Then, if the angle measured by the line in the x- axis measured in positive direction of the x- axis, measured in anticlockwise direction is-

\( 90^{\circ} + 60^{\circ} = 150^{\circ} \)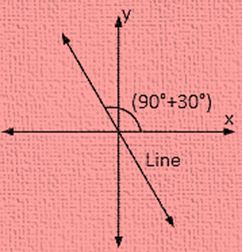

 

Therefore, the slope of the given line is tan \( 150^{\circ} \) = tan( \( 180^{\circ} – 30^{\circ} )\) = – tan \( 30^{\circ}\) = \(\frac{ 1 }{ \sqrt{ 3 }}\).

 

 

Q-8. What will be the value of a so that the points (a, -2), (3, 2) and (5, 6) get collinear to each other?

Solution. Based on formulae given in Straight Lines

Let us assume that, the points X (a, -2), Y (3, 2) and Z (5, 6) are collinear.

Now,

Slope of XY = Slope of YZ

\(\Rightarrow \frac{2 – \left ( -2 \right )}{ 3 – a } = \frac{ 6 – 2 }{ 5 – 3 }\) \(\Rightarrow \frac{2 + 2 }{ 3 – a } = \frac{ 4 }{ 2 }\) \(\Rightarrow \frac{ 4 }{ 3 – a } = 2 \)

4 = 6 – 2a

2a = 2

a = 1

Therefore, the value of a = 1.

 

 

Q-9. Prove that the points (-3, -2), (5, 0), (4, 4) and (-4, 2) are the vertices of a parallelogram without using the distance formula.

Solution. Based on formulae given in Straight Lines

Let us denote the given points as P (-3, -2), Q (5, 0), R (4, 4) and S (-4, 2).

 

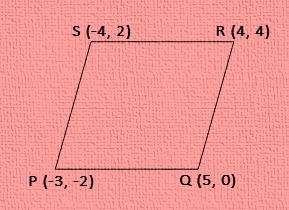
Now,

Slope of the side PQ = \(\frac{ 0 + 2 }{ 5 + 3 } = \frac{ 2 }{ 8 } = \frac{ 1 }{ 4 }\)

Slope of the side RS = \(\frac{ 2 – 4 }{ -4 – 4 } = \frac{ -2 }{ -8 } = \frac{ 1 }{ 4 }\)

Thus,

Slope of the side PQ = Slope of the side RS

Hence,

PQ and RS are parallel to each other.

 

Now,

Slope of the side QR = \(\frac{ 4 – 0 }{ 4 – 5 } = \frac{ 4 }{ -1 } = -4 \)

Slope of the side PS = \(\frac{ 2 + 2 }{ -4 + 3 } = \frac{ 4 }{ -1 } = -4 \)

Thus,

Slope of the side QR = Slope of the side PS

Hence,

QR and PS are parallel to each other.

Hence, both of the opposite side‘s pairs of the quadrilateral PQRS are parallel. Thus, PQRS is a parallelogram.

Therefore, the given points P (-3, -2), Q (5, 0), R (4, 4) and S (-4, 2) are the vertices of the parallelogram.

 

 

Q-10. Consider two points (4, -2) and (5, -3). What is the angle between the x- axis and the line joining the given two points?

Solution. Based on formulae given in Straight Lines

The slope of the line joining the given two points, namely, X (4, -2) and Y (5, -3) is given by:

M = \(\frac{ -3 – \left( -2 \right ) }{ 5 – 4 }\) = -3 + 2 = -1

Thus,

The angle of inclination, say \(\Theta \), of the line joining the given points X (4, -2) and Y (5, -3) is:

tan\(\Theta \) = m = -1

Since, \(\Theta \) is (\(90^{\circ} – 45^{\circ}\) ) = \(135^{\circ}\)

Therefore, between the x- axis and the line joining the given two points, the angle of inclination is \(135^{\circ}\).

 

 

Q-11. Assume that the slope of a line AB is twice the slope of the other line PQ. Get all the slopes of the lines when the tangent of the angle between them is \(\frac{ 1 }{ 3 }\).

Solution. Based on formulae given in Straight Lines

Let us assume that, the slope of the given two lines be m₁ and m₂, so that

m₂ = 2 m₁

Now,

It is known that if \(\Theta \) is the angle between the two given lines, namely AB and PQ, whose slopes are m₁ and m₂, then

tan\(\Theta \) = \(\left | \frac{ m_{ 2 } – m_{ 1 } }{ 1 + m_{ 1 } m_{ 2 }} \right |\)

According to the question, the tangent of the angle between the two given lines is \(\frac{ 1 }{ 3 }\).

\(\frac{ 1 }{ 3 }\) = \(\left | \frac{ 2m_{ 1 } – m_{ 1 } }{ 1 + m_{ 1 } \times 2m_{ 1 }} \right |\)

\(\Rightarrow \frac{ 1 }{ 3 } = \left | \frac{ -m_{ 1 } }{ 1 + \left (2m_{ 1 } \right )^{ 2 }} \right |\) \(\Rightarrow \frac{ 1 }{ 3 } = \frac{ -m_{ 1 } }{ 1 + \left (2m_{ 1 } \right )^{ 2 }} \; or \; \frac{ 1 }{ 3 } = -\left (\frac{ -m_{ 1 } }{ 1 + \left (2m_{ 1 } \right )^{ 2 }} \right ) = \frac{ m_{ 1 } }{ 1 + \left (2m_{ 1 } \right )^{ 2 }} \)

CASE- I:

\(\Rightarrow \frac{ 1 }{ 3 } = \frac{ -m_{ 1 } }{ 1 + \left (2m_{ 1 } \right )^{ 2 }}\) \(\Rightarrow 1 + \left ( 2m_{ 1 } \right )^{ 2 } = -3 m_{ 1 }\) \(\Rightarrow 1 + 3 m_{ 1 } + \left ( 2m_{ 1 } \right )^{ 2 } = 0 \) \(\Rightarrow \left ( 2m_{ 1 } \right )^{ 2 } + 2 m_{ 1 } + m_{ 1 } + 1 = 0 \) \(\Rightarrow 2m_{ 1 } \left ( m_{ 1 } + 1 \right ) + 1\left ( m_{ 1 } + 1 \right ) = 0\) \(\Rightarrow \left ( m_{ 1 } + 1 \right ) \left ( 2m_{ 1 } + 1 \right ) = 0\) \(\Rightarrow m_{ 1 } = -1 \; or \; m = -\frac{ 1 }{ 2 }\)

Let, m₁ = -1, then the slopes of the lines are -1 and -2.

Let, \( m = -\frac{ 1 }{ 2 }\), then the slopes of the given lines, namely AB and PQ are \( -\frac{ 1 }{ 2 }\) and -1.

 

CASE- II:

\(\Rightarrow \frac{ 1 }{ 3 } = \frac{ m_{ 1 } }{ 1 + \left (2m_{ 1 } \right )^{ 2 }}\) \(\Rightarrow 1 + \left ( 2m_{ 1 } \right )^{ 2 } = 3 m_{ 1 }\) \(\Rightarrow 1 – 3 m_{ 1 } + \left ( 2m_{ 1 } \right )^{ 2 } = 0 \) \(\Rightarrow \left ( 2m_{ 1 } \right )^{ 2 } – 2 m_{ 1 } – m_{ 1 } + 1 = 0 \) \(\Rightarrow 2m_{ 1 } \left ( m_{ 1 } – 1 \right ) – 1\left ( m_{ 1 } – 1 \right ) = 0\) \(\Rightarrow \left ( m_{ 1 } – 1 \right ) \left ( 2m_{ 1 } – 1 \right ) = 0\) \(\Rightarrow m_{ 1 } = 1 \; or \; m = \frac{ 1 }{ 2 }\)

Let, m₁ = 1, then the slopes of the lines are 1 and 2.

Let, \( m = \frac{ 1 }{ 2 }\), then the slopes of the given lines namely, AB and PQ are \( \frac{ 1 }{ 2 }\) and 1.

Therefore, the slopes of the lines AB and PQ are -1 and -2 or, \( -\frac{ 1 }{ 2 }\) and -1 or, \( \frac{ 1 }{ 2 }\) and 1 or, 1 and 2.

 

 

Q-12. Consider a line passing through two points (a₁, b₁) and (j, k). Assume that the slope of the line passing through these points is m. Prove that:

k – b₁ = m (j – a₁).

Solution. Based on formulae given in Straight Lines

As we know that:

The slope of the line, say AB, passing through the two given points (a₁, b₁) and (j, k) is given by:

\(\frac{ k – b_{ 1 } }{ j – a_{ 1 } }\)

\(\frac{ k – b_{ 1 } }{ j – a_{ 1 } }\) = m

\(\Rightarrow k – b_{ 1 } = m \left (j – a_{ 1 } \right )\)

Therefore, \(\Rightarrow k – b_{ 1 } = m \left (j – a_{ 1 } \right )\).

Hence, proved.

 

 

Q-13. Assume that the three points (a, 0), (p, r) and (0, h) lies on the same line. Prove that:

\(\frac{ p }{ a } + \frac{ r }{ h } = 1 \).

Solution. Based on formulae given in Straight Lines

As per the given condition in the question,

Points X( a, 0 ), Y( p, r ) and Z( 0, h ) lies on the same line, then

The slope of XY = The slope of YZ

\(\Rightarrow \frac{ r – 0 }{ p – a } = \frac{ h – r }{ 0 – p }\) \(\Rightarrow \frac{ r }{ p – a } = \frac{ h – r }{ – p }\)

-pr = (h – r) (p – a)

-pr = hp – ha – rp + ra

hp + ra = ha

Dividing both side by ha, we will get

\(\frac{ hp }{ ha } + \frac{ ra }{ ha } = \frac{ ha }{ ha }\) \(\Rightarrow \frac{ p }{ a } + \frac{ r }{ h } = 1 \)

Hence, proved.

 

 

Q-14. Take the records of population and year graph given below. What will be the slope of the line XY? By using this, find the population in the year 2005.

 

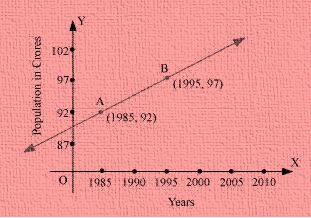
Solution. Based on formulae given in Straight Lines

Here we can observe that the line XY passes through points X (1985, 90) and Y (1995, 95).

Then, the slope of the line XY is given by

\( \frac{ 95 – 90 }{ 1995 – 1985 } = \frac{ 5 }{ 10 } = \frac{ 1 }{ 2 }\\\)

Let, a be the population of the year 2005.

Then, as per the data in the graph, the line XY will exactly pass through the point Z( 2005, y ).

Slope of XY = Slope of YZ

\(\Rightarrow \frac{ 1 }{ 2 } = \frac{ y – 95 }{ 2005 – 1995 }\) \(\Rightarrow \frac{ 1 }{ 2 } = \frac{ y – 95 }{ 10 }\) \(\Rightarrow \frac{ 10 }{ 2 } = y – 95\\\)

So, y – 95 = 5

So, y = 100

Hence, the slope of the line XY is \(\frac{ 1 }{ 2 }\), whereas, in the year 2005, the expected population will be about 100 crores.

 

 

Exercise – 10.2

Q-1. Write all the possible equations for the two axis, which is x- axis and y- axis.

Solution. Based on formulae given in Straight Lines

As we know that,

The x- coordinates at all the points on the y- axis is 0.

So, the equations on the y – axis is y = 0.

The y- coordinates at all the points on the x- axis is 0.

So, the equations on the x – axis is x = 0.

 

Q-2. Write the equation for the line which passes through the point (-5, 4) with having slope \(\frac{ 1 }{ 4 }\).

Solution. Based on formulae given in Straight Lines

It is known that the equation for the line passing through any point, say, (x₀, y₀), with having slope m, is given by-

(y – y₀) = m (x – x₀)

Therefore, the equation for the line passing through (-5, 4) with having slope \(\frac{ 1 }{ 4 }\), is

(y – 4) = \(\frac{ 1 }{ 4 }\)( x – ( -5 ))

(y – 4) = \(\frac{ 1 }{ 4 }\)( x + 5 )

4(y – 4) = (x + 5)

4y – 16 = x + 5

i.e., x – 4y + 11 = 0

Hence, the equation of the line which passes through (-5, 4) is given by-

x – 4y + 11 = 0

 

Q-3. Write the equation for the line which passes through the point (0, 0) with having slope S.

Solution. Based on formulae given in Straight Lines

It is known that the equation for the line passing through any point, say, (x₀, y₀), with having slope m, is –

(y – y₀) = m (x – x₀)

Therefore, the equation for the line passing through (0, 0) with having slope S, is

(y – 0) = S (x – 0)

i.e., y = Sx

Hence, the equation of the line which passes through (0, 0) is given by-

y = Sx

Q-4. Write the equation for the line which passes through ( 3, 3\(\sqrt{ 3}\) ) which is inclined on x- axis at an angle \(75^{\circ}\).

Solution. Based on formulae given in Straight Lines

The slope of the line inclined on the x- axis at an angle \(75^{\circ}\) is m = tan \(75^{\circ}\)

\(\Rightarrow m = tan\left ( 45^{\circ} + 30^{\circ} \right )\) \(\Rightarrow m = \frac{ tan 45^{\circ} + tan 30^{\circ} }{ 1 – tan 45^{\circ} . tan 30^{\circ} }\) \(\Rightarrow m = \frac{ 1 + \frac{ 1 }{ \sqrt{ 3 } } }{ 1 – 1.\frac{ 1 }{ \sqrt{ 3 } }} = \frac{\frac{ \sqrt{ 3 } + 1 }{ \sqrt{ 3 } }}{ \frac{ \sqrt{ 3 } – 1 }{ \sqrt{ 3 } } }\) \(\Rightarrow m = \frac{ \sqrt{ 3 } + 1 }{ \sqrt{ 3 } – 1 }\)

It is known that the equation for the line passing through any point, say, ( x₀, y₀ ), with having slope m, is –

(y – y₀) = m (x – x₀)

Therefore, the equation for the line passing through ( 3, 3\(\sqrt{ 3 }\) ) inclined at an angle of \(75^{\circ}\) on the x- axis is given by:

( y – 3\(\sqrt{ 3 }\) ) = \( \frac{ \sqrt{ 3 } + 1 }{ \sqrt{ 3 } – 1 }\) ( x – 3 )

( y – 3\(\sqrt{ 3 }\) ) ( \(\sqrt{ 3 }\) – 1 ) = (\(\sqrt{ 3 }\) + 1 )( x – 3 )

y (\(\sqrt{ 3 }\) – 1 ) – 3\(\sqrt{ 3 }\)( \(\sqrt{ 3 }\) – 1 ) = x ( \(\sqrt{ 3 }\) + 1 ) – 3( \(\sqrt{ 3 }\) + 1 )

( \(\sqrt{ 3 }\) + 1 )x – ( \(\sqrt{ 3 }\) – 1 )y = 3\(\sqrt{ 3 }\) + 3 – 9 + 3\(\sqrt{ 3 }\)

( \(\sqrt{ 3 }\) + 1 )x – ( \(\sqrt{ 3 }\) – 1 )y = 6\(\sqrt{ 3 }\) – 6

i.e., ( \(\sqrt{ 3 }\) + 1 )x – ( \(\sqrt{ 3 }\) – 1 )y = 6( \(\sqrt{ 3 }\) – 1 )

Hence, the equation of the line which passes through ( 3, 3\(\sqrt{ 3 }\) ) is given by-

( \(\sqrt{ 3 }\) + 1 )x – ( \(\sqrt{ 3 }\) – 1 )y = 6( \(\sqrt{ 3 }\) – 1 )

 

 

Q-5. Write the equation for the line which intersects x – axis at a distance 4 units away from the left side of the origin having slope -3.

Solution. Based on formulae given in Straight Lines

We know that,

If a line having slope m intersects x- axis at a distance d, then the equation of such lines is given by:

y = m(x – d)

Thus, The equation of the line intersecting x- axis at a distance 4 units from the left side of the origin, i.e., d = -4, and having slope m = -3, is given by:

y = -3[x – (- 4)]

y = -3x – 12

Therefore, the equation of the line required is given by:

3x + y + 12 = 0

 

 

Q-6. Write the equation for the line which intersects the y – axis at a distance 3 units above the origin which makes an angle \(60^{\circ}\) along the positive direction of the corresponding axis, i.e., x- axis.

Solution. Based on formulae given in Straight Lines

We know that,

If a line having slope m makes a y- intercept c, then the desired equation for the line is given by:

y = mx + c

Since, c = 3 units and makes an angle of \(60^{\circ}\) along the positive direction of the x- axis, i.e.,

m = tan\(60^{\circ}\) = \(\sqrt{ 3 }\)

Therefore, the equation of the line required is:

y = \(\sqrt{ 3 }\)x + 3

i.e., \(\sqrt{ 3 }\)x – y + 3 = 0

 

 

Q-7. Write the equation of the line passing through the two points (-2, 2) and (3, -5).

Solution. Based on formulae given in Straight Lines

We know that,

\(m = \frac{ y_{ 2 } – y_{ 1 } }{ x_{ 2 } – x_{ 1 } }\)

Also, the equation for the line passing through the two given points (x₁, y₁) and (x₂, y₂) is given by:

y – y₁ = \( \frac{ y_{ 2 } – y_{ 1 } }{ x_{ 2 } – x_{ 1 } }\) ( x – x₁ )

Hence, the required equation for the line which passes through (-2, 2) and (3, -5) is

y – 2 = \( \frac{ -5 – 2 }{ 3 – \left( -2 \right ) }\) ( x + 2 )

y – 2 = \(\frac{ -7 }{ 5 }\)( x + 2 )

5(y – 2) = -7 (x + 2)

5y – 10 = -7x – 14

7x + 5y + 4 = 0

Therefore, the required equation is 7x + 5y + 4 = 0

 

 

Q-8. Write the equation for the line which is at a perpendicular distance of 7 units from the point (0, 0) and the perpendicular makes an angle of \(45^{\circ}\) along the positive x- axis.

Solution. Based on formulae given in Straight Lines

Let, k be the length of the normal from the origin to a line and \(\Theta \) be the angle of the normal to a line in the positive direction of the x- axis, then

The equation of the line is:

\(a cos\Theta + b sin\Theta = k\)

Since, k = 5 units and \(\Theta = 45^{\circ} \)

Therefore,

The equation of the line satisfying the conditions is given by:

\(a cos 45^{\circ} + b sin 45^{\circ} = 7\) \(a \frac{ 1 }{ \sqrt{ 2 } } + b \frac{ 1 }{ \sqrt{ 2 } } = 7\)

i.e., \(a + b = 7\sqrt{ 2 }\)

i.e., \( a + b – 7\sqrt{ 2 } = 0 \)

 

 

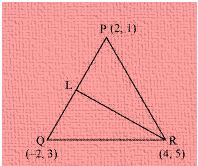
Q-9. Consider a triangle ABC whose vertices are A (3, 2), B (-3, 4) and C (5, 6). Write the equation for the median through one of the vertex of the triangle say, C.

Solution. Based on formulae given in Straight Lines

As per the data given in the question,

The vertices of the \(\Delta \)ABC are A( 3, 1 ), B( -3, 4 ) and C( 5, 6 ).

Let us assume that, CM be the median of the triangle through vertex C.

It means, M is the mid- point of the side AB.

Now, by mid- point theorem, the required coordinates of the point M is given by:

\(\left ( \frac{ 3 – 3 }{ 2 }, \frac{ 2 + 4 }{ 2 } \right )\) = ( 0, 3 )

 

We know that, the equation for the line passing through the two given points (a₁, b₁) and (a₂, b₂) is given by:

b – b₁ = \( \frac{ b_{ 2 } – b_{ 1 } }{ a_{ 2 } – a_{ 1 } }\) ( a – a₁ )

Here, (a₁, b₁) = (5, 6) and (a₂, b₂) = (0, 3)

So, by substitution these values in the equation for the line CM passing through two given points is:

(b – 6) = \(\frac{ 3 – 6 }{ 0 – 5 }\)( a – 5 )

(b – 6) = \(\frac{ 3 }{ 5 }\)( a – 5 )

5 (b – 6) = 3 (a – 5)

5b – 30 = 3a – 15

3a – 5b + 15 = 0

Therefore, the equation of the median through vertex R is 3a – 5b + 15 = 0

 

 

Q-10. Get the equation for the line which is passing through (-4, 5) and which is perpendicular to the line passing through two points (3, 6) and (-4, 7).

Solution. Based on formulae given in Straight Lines

We know that,

\(m = \frac{ y_{ 2 } – y_{ 1 } }{ x_{ 2 } – x_{ 1 } }\)

So, the slope of the line joining the two given points, namely A (3, 6) and B (-4, 7), i.e.,

m = \(\frac{ 7 – 6 }{ -4 – 3 } = \frac{ 1 }{ -7 }\)

Now,

It is known that the two non- vertical lines are perpendicular to each other if and only if each of their slopes is a negative reciprocal of each other.

Hence, the slope of the line which is perpendicular to the line through the given points (3, 6) and (-4, 7) is:

\(-\frac{ 1 }{ m } = -\frac{ 1 }{ \frac{ -1 }{ 7 } } = 7\)

Hence, the equation for the line passing through the point (-4, 6), having slope 7 is given by:

(y – 6) = 7 (x + 4)

y – 5 = 7x + 28

i.e., 7x – y + 33 = 0

Therefore, the required equation for the line is 7x – y + 33 = 0

 

 

Q-11. Consider a line which is perpendicular to the line segment joining the two points (2, 0) and (3, 4) dividing it in 1 : p ratio. Find the equation for such a line.

Solution. Based on formulae given in Straight Lines

By having the section formula, we know that

The coordinates of the point dividing the line segment joining the two points (2, 0) and (3, 4) in the ratio 1 : p which is given by:

\(\left ( \frac{ p \left ( 2 \right ) + 2 \left ( 3 \right )}{ 1 + p }\; , \; \frac{ p \left ( 0 \right ) + 2 \left ( 4 \right )}{ 1 + p } \right ) = \left ( \frac{ 2p + 6 }{ p + 1 } , \frac{ 8 }{ p + 1 }\right )\)

Now, the slope for the line joining the two given points (2, 0) and (3, 4) is given by:

m = \(\frac{ 4 – 0 }{ 3 – 2 } = \frac{ 4 }{ 1 } \) = 4

It is known that the two non- vertical lines are perpendicular to each other if and only if each of their slopes is a negative reciprocal of each other.

Hence, The slope of the line which is perpendicular to the line through the given points (2, 0) and (3, 4 ) is:

\(-\frac{ 1 }{ m } = -\frac{ 1 }{ 4 } \)

Hence, the equation for the line passing through the point \(\left ( \frac{ 2p + 6 }{ p + 1 } , \frac{ 8 }{ p + 1 }\right )\), having slope \( -\frac{ 1 }{ 4 } \) is given by:

\(\Rightarrow\) \(\left (y\; -\; \frac{ 8 }{ p + 1 } \right ) = -\frac{ 1 }{ 4 } \left ( x \;-\; \frac{ 2p + 6 }{ p + 1 } \right )\\\)

\(\\\Rightarrow\) \(4\left (y\; – \;\frac{ 8 }{ p + 1 } \right ) = -\left ( x\; – \;\frac{ 2p + 6 }{ p + 1 } \right )\)

\(\Rightarrow\) \(4\left (p + 1 \right )y – 32 = -x\left ( p + 1 \right ) + \left ( 2p + 6 \right )\)

\(\Rightarrow\) \(x\left (p + 1 \right) – 4\left (p + 1 \right)y = -\left( 2p + 6 – 32 \right )\)

\(\Rightarrow\) \(x\left (p + 1 \right) – 4\left (p + 1 \right)y = 26 – 2p\)

Therefore, the equation is \(\Rightarrow x\left (p + 1 \right) – 4\left (p + 1 \right)y = 26 – 2p\).

 

 

Q-12. What will be the equation for the line which cuts off intercepts equally on the co-ordinate axes and which passes through the point (3, 4).

Solution. Based on formulae given in Straight Lines

It is known that, the equation of any line in the intercept form is:

\(\frac{ x }{ m } + \frac{ y }{ n } = 1 \) …………(i)

Where, m and n are intercepts on the x- axis and y- axis, respectively.

From the data given in the question it is known that, the line cuts off an equal intercepts on the co-ordinate axes, which clearly means that m = n.

So, from equation (i), we have

\(\frac{ x }{ m } + \frac{ y }{ m } = 1 \)

\(\Rightarrow x + y = m \) …………..(ii)

Thus, the line passes through the point (3, 4), equation ( ii ) reduces to

3 + 4 = m

So, m = 7

On substituting the value of m in equation (ii), we will get

x + y = 7

Hence, the equation of the line required is x + y = 7.

 

Q-13. A line is passing through (3, 3) and making intercepts on the coordinate axes. The sum of the two intercepts is 12. Find the equation of the line.

Solution. Based on formulae given in Straight Lines

It is known that, the equation of any line in the intercept form is:

\(\frac{ x }{ m } + \frac{ y }{ n } = 1 \) …………(i)

Where, m and n are intercepts on the x- axis and y- axis, respectively.

From the data given in the question it is known that,

m + n = 12

So, m = 12 – n

Substituting the value of m in equation (i), we will get

\(\frac{ x }{ 12 – n } + \frac{ y }{ n } = 1 \) …………(ii)

Since, the line is passing through the point (3, 3). Hence, from equation (ii), we will get

\(\frac{ 3 }{ 12 – n } + \frac{ 3 }{ n } = 1\\\)

\(\Rightarrow\) \(\frac{ 3( n ) + 3 ( 12 – n )}{ n ( 12 – n )} = 1\)

\(\\\Rightarrow\) \(\frac{ 3n + 36 – 3n }{ 12n – n^{ 2 }} = 1\)

\(\Rightarrow\) \(\frac{ 36 }{ 12n – n^{ 2 }} = 1 \)

\(\Rightarrow\) \(36 = 12n – n^{ 2 }\)

\(\Rightarrow n^{2}\) \(– 12n + 36 = 0\)

\(\Rightarrow\) \(n^{ 2 } – 6n – 6n + 36 = 0\)

\(\Rightarrow\) \(n\left( n – 6 \right ) – 6\left( n – 6 \right )\)

(n – 6) (n – 6) = 0

So, n = 6 or n = 6

Now,

As n = 6, so m = 6

Hence, the required equation of the line is given by:

\(\frac{ x }{ 6 } + \frac{ y }{ 6 } = 1\\\)

Therefore, Equation is x + y = 6.

Q-14. Write the equation for the line which is passing through (0, 3) and makes an angle

\(\frac{ \pi }{ 6 }\) along the positive direction of x- axis. Also, find the equation for the line which is parallel to it and which crosses the y-axis at the distance of 3 units to the negative direction of y- axis from (0, 0).

Solution. Based on formulae given in Straight Lines

As the line is making an angle \(\frac{ \pi }{ 6 }\) in the positive direction of x- axis,

So the slope of the line is m = tan\(\frac{ \pi }{ 6 }\) = tan\( 30^{\circ}\) = \(\frac{ 1 }{ \sqrt{ 3 }}\)

Thus, the equation of the line which is passing through (0, 3) and having slope \(\frac{ 1 }{ \sqrt{ 3 }}\) is

(y – 3) = \(\frac{ 1 }{ \sqrt{ 3 }}\) ( x – 0 )

\( \sqrt{ 3 } \)( y – 3 ) = x

i.e., x – \( \sqrt{ 3 } \)y + 3\( \sqrt{ 3 } \) = 0

Hence, the slope of the line parallel to x – \( \sqrt{ 3 } \)y + 3\( \sqrt{ 3 } \) = 0 is \(\frac{ 1 }{ \sqrt{ 3 }}\) to the line.

In the question, it is given that the line parallel to x – \( \sqrt{ 3 } \)y + 3\( \sqrt{ 3 } \) = 0 crosses y- axis at a distance 3 units to the negative direction of y- axis from the origin, i.e., it passes through point ( 0, -3 ).

Therefore, the equation of the line which is passing through ( 0, -3 ) and having slope \(\frac{ 1 }{ \sqrt{ 3 }}\) is:

y – ( -3 ) = \(\frac{ 1 }{ \sqrt{ 3 }}\) ( x – 0 )

y + 3 = \(\frac{ 1 }{ \sqrt{ 3 }}\) ( x – 0 )

\( \sqrt{ 3 } \)( y + 3 ) = x

i.e., x – \( \sqrt{ 3 } \)y – 3\( \sqrt{ 3 } \) = 0

Hence, the required equation of the line = x – \( \sqrt{ 3 } \)y – 3\( \sqrt{ 3 } \) = 0.

 

Q-15. What will be the equation of the line perpendicular to the line from the origin meets at (-3, 10)?

Solution. Based on formulae given in Straight Lines

The slope of the line which joins (0, 0) and the point (-3, 10) is

m = \(\frac{ 10 – 0 }{ -3 – 0 } = -\frac{ 10 }{ 3 }\)

So, accordingly, the slope of the line which is perpendicular to the line joining (0, 0) and the point (-3, 10) is-

m₁ = –\(\frac{ 1 }{ m } = -\frac{ 1 }{ \frac{ -10 }{ 3 }} = { 3 } { 10 }\)

Thus, the equation of the line which passes from (-3, 10) and having slope m₁ is given by

(y – 10) = \( { 3 } { 10 }\)( x + 3 )

10( y – 10 ) = 3 ( x + 3 )

10y – 100 = 3x + 9

i.e., 30x – 10 y + 91 = 0

Hence, the required equation of the line is 30x – 10 y + 91 = 0

 

 

Q-16. Consider a copper rod having length L (in centimeters) which is a linear function of the Celsius temperature which is C. Express L in terms of C, for an experiment. Assume that, L = 127.952 when C = 24, and L = 128.987 when C = 114.

Solution. Based on formulae given in Straight Lines

As per the data given in the question, we have

If C = 24, then the value of L = 127.952, whereas if C = 114, then the value of L = 128.987.

So, the points are (24, 127.952) and (114, 128.987) which satisfies the linear relation between L and C.

Consider L along the y- axis and C along the x- axis and also, we have two points i.e., (24, 127.952) and (114, 128.987) in XY plane.

Hence, the linear relation of the line between C and L which is passing through (24, 127.952) and (114, 128.987) is given by:

(L – 127.952) = \(\frac{ 128.987 – 127.952 }{ 114 – 24 }\)( C – 24 )

L – 127.952 = \(\frac{ 1.035 }{ 90 }\)(C – 24)

i.e., L = \(\frac{ 1.035 }{ 90 }\)( C – 24 ) + 127.952

Hence, the linear relation between C and L required = L = \(\frac{ 1.035 }{ 90 }\)( C – 24 ) + 127.952

 

 

Q-17. A milk store owner observed that, he can sell at least 1000 liters of milk every week at a price of Rs. 15/liter and also, 1240 liters of milk every week at a price of Rs. 17/liter. Consider a linear relation between the demand and estimated selling price, find how many liters would he will sell every week at a cost of Rs.18/liters?

Solution. Based on formulae given in Straight Lines

It is given in the question that there is a linear relation between the selling price and the demand.

Consider demand along the y- axis and the estimated selling price per liter along the x- axis. (15, 1000) and (17, 1240) are the two given points along the XY plane which satisfies the linear relation between the selling price and the demand.

Hence, the linear relation of the line between S (Selling price) and D (demand) which is passing through (15, 1000) and (17, 1240) is given by:

y – 1000 = \(\frac{ 1240 – 1000 }{ 17 – 15 } = \frac{ 240 }{ 2 } = 120 \)( x – 15 )

y – 1000 = \( \frac{ 240 }{ 2 } \)( x – 15 )

y – 1000 = 120 (x – 15)

i.e., y = 120 (x – 15) + 1000

If, x = Rs. 18/liters

y = 120(18 – 15) + 1000

y = 120 (3) + 1000

y = 1360

Hence, the milk store owner will sell 1360 liters of milk weekly at the rate of Rs. 18/liter.

 

 

Q-18. S (m, n) be the mid-point of the line- segment between the axes. Prove that the equation of such line is-

\(\frac{ x }{ m } + \frac{ y }{ n } = 2 \)

Solution. Based on formulae given in Straight Lines

Let, PR be the line segment between the axes and let, S (m, n) be its mid-point.

 

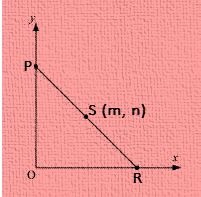
Thus, the co-ordinates of P and R be (0, y) and (x, 0), respectively.

As, point S (m, n) is the mid-point of the line PR.

So, \(\left( \frac{ 0 + x }{ 2 },\; \frac{ y + 0 }{ 2 } \right ) = \left( m, n \right )\)

\(\Rightarrow \left( \frac{ x }{ 2 },\; \frac{ y }{ 2 } \right ) = \left( m, n \right )\) \(\Rightarrow \frac{ x }{ 2 } = m \; and \; \frac{ y }{ 2 } = n \)

x = 2m and y = 2n

Hence, the coordinates of P and R are (0, 2n) and (2m, 0).

Therefore, the equation of the line which is passing through the points (0, 2n) and (2m, 0) is given by:

(y – 2n) = \(\frac{ 0 – 2n }{ 2m – 0 }\) ( x – 0 )

(y – 2n) = \(\frac{ -2n }{ 2m }\)( x – 0 )

(y – 2n) = \(\frac{ -n }{ m }\)( x )

m (y – 2n) = -n( x )

my – 2mn = -nx

i.e., nx + my – 2mn = 0

By dividing both side with mn, we will get

\(\frac{ nx }{ mn } + \frac{ my }{ mn } – \frac{ 2mn }{ mn } = 0 \) \(\frac{ x }{ m } + \frac{ y }{ n } – 2 = 0\) \(\frac{ x }{ m } + \frac{ y }{ n } = 2\)

Hence, the required equation of the line is \(\frac{ x }{ m } + \frac{ y }{ n } = 2\).

Q-19. The point R (m, n) divides the line segment PQ in the ratio of 2: 3 between both the axes. What will be the equation of the line?

Solution. Based on formulae given in Straight Lines

As per the data given in the question, we know that PQ is the line segment which is divided in the ratio of 2 : 3 by the point R (m, n).

 

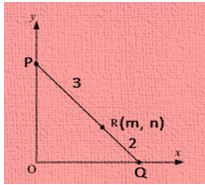
Let, the coordinates of P and Q is (x, 0) and (0, y), respectively.

As we know, PQ is the line segment which is divided in the ratio of 2 : 3 by the point R( m, n ).

By using the section formula,

( m, n ) = \(\frac{ 2 \times 0 + 3 \times x }{ 2 + 3 },\; \frac{ 2 \times y + 3 \times 0 }{ 2 + 3 }\)

⇒ \(( m,\;n ) = \left(\frac{3x}{5}, \; \frac{2y}{5}\right)\)

\(\\\Rightarrow\) \(m = \frac{ 3x }{ 5 } \; and \; n = \frac{ 2y }{ 5 }\)

\(\Rightarrow\) \(x = \frac{ 5m }{ 3 } \; and \; y = \frac{ 5n }{ 2 }\)

Thus, the coordinates of P and Q are ( \(\frac{ 5m }{ 3 }\), 0 ) and ( 0, \(\frac{ 5n }{ 2 }\) ).

Then,

The equation for the line PQ which is passing through points \(\left ( \frac{ 5m }{ 3 }, 0 \right ) \;and\; \left ( 0,\frac{ 5n }{ 2 } \right )\) is given by:

(y – 0) = \(\left( \frac{ \frac{ 5n }{ 2 } – 0 }{ 0 – \frac{ 5m }{ 3 } } \right ) ( x – \frac{ 5m }{ 3 })\)

y = \(\left( \frac{ 5n \times 3 }{ -5n \times 2 } \right ) \left( x – \frac{ 5m }{ 3 } \right )\)

y = \(\frac{ -3n }{ 2m } \left( x – \frac{ 5m }{ 3 } \right )\)

\(\Rightarrow\) \(2m \times y = -3n \times \frac{ 3x – 5m }{ 3 }\)

\(\Rightarrow\) \(2m \times y \times 3 = -3n \times 3x + 3n \times 5m \)

6my = -9nx + 15mn

9nx + 6my – 15mn = 0

3(3nx + 2my – 5 mn) = 0

i.e., 3nx + 2my – 5mn = 0

Hence, the equation of the line PQ required is given by 3nx + 2my – 5mn = 0.

Q-20. Show that the three points (4, 1), (-3, -3) and (11, 5) are collinear by using the concept of the equation of a line.

Solution. Based on formulae given in Straight Lines

If we will prove that the line which passes through the points (4, 1) and (-3, -3) passes through the point (11, 5) also, then we can prove that the three points (4, 1), (-3, -3) and (11, 5) are collinear.

Now, the required equation of the line passing through (4, 1) and (-3, -3) will be given by:

(y – 1) = \(\frac{ -3 – 1 }{ -3 – 4 }\)( x – 4 )

y – 1 = \(\frac{ -4 }{ -7 }\)( x – 4 )

7y – 7 = 4 (x – 4)

7y = 4x – 16 + 7

4x – 7y = 9

Since, the line passes through the point (11, 5), so, x = 11 and y = 5

Now,

LHS = 4 × 11 – 7 × 5 = 44 – 35 = 9 = RHS

Hence, the line which is passing through the points (4, 1) and (-3, -3) also passes through the other point (11, 5). Hence, (4, 1), (-3, -3) and (11, 5) are collinear.

 

 

Exercise 10.3

Q1. Reduce the following equations into slope-intercept form and find their slopes and the y intercepts.

(i) x + 6y = 0

(ii) 6x + 3y – 6 = 0

(iii) y = 1

Sol: Based on formulae given in Straight Lines

(i) x + 6y = 0

It can be written as:

\(y = -\frac{1}{6}a + 0\) ————–(1)

The given equation is in the form of y = mx + c,

Where \(m = -\frac{1}{7}\) and c = 0

Hence, equation (1) is in the slope – intercept form, where the slope and the y – intercept are \(-\frac{1}{6}\) and 0 respectively.

(ii) 6x + 3y – 6 = 0

It can be written as:

\(y = \frac{1}{3}\left ( -6x + 6 \right )\)

\(y = -2x + \frac{6}{3}\) —————— (2)

The given equation is in the form of y = mx + c,

Where m = – 2 and c = 2

Hence, equation (2) is in the slope – intercept form, where the slope and the y – intercept are -2 and 3 respectively.

(iii) y = 1

It can be written as:

y = 0.x + 1 —————— (3)

The given equation is in the form of y = mx + c,

Where m = 0 and c = 1

Hence, equation (3) is in the slope – intercept form, where the slope and the y – intercept are 0 and 1 respectively.

 

 

Q2. Reduce the following equations into intercept form and find their intercepts on the axes.

(i) 3x + 2y – 14 = 0

(ii) 4x – 3y = 6

(iii) 3y + 2 = 0

Sol: Based on formulae given in Straight Lines

(i) 3x + 2y – 14 = 0

It can be written as:

3x + 2y = 14

\(\frac{3x}{14} + \frac{2y}{14} = 1\)

\(\frac{3x}{14} + \frac{y}{7} = 1\) ————— (1)

The given equation is in the form of \(\frac{x}{a} + \frac{y}{b} = 1\)

Where a = 14 / 3 and b = 7.

Hence, equation (1) is in intercept form, where the intercepts on the x and y axes are 14 / 3 and 7 respectively.

(ii) 4x – 3y = 12

It can be written as:

\(\frac{4x}{12} – \frac{3y}{12} = 1\) \(\frac{x}{3} – \frac{y}{4} = 1\)

\(\frac{x}{3} + \frac{y}{- 4} = 1\) ————– (2)

The given equation is in the form of \(\frac{x}{a} + \frac{y}{b} = 1\)

Where a = 3 and b = – 4.

Hence, equation (2) is in the intercept form, where the intercepts on the x and y axes are 3 and – 4 respectively.

(iii) 3y + 4 = 0

It can be written as:

3y = – 4

\(\frac{y}{\left (-\frac{4}{3} \right )} = 1\) ——————(3)

The given equation is in the form of \(\frac{x}{a} + \frac{y}{b} = 1\)

Where a = 3 and b = – 4.

Hence, equation (3) is in the intercept form, where the intercepts on the x and y axes are 0 and \(-\frac{2}{3}\) respectively.

 

 

Q3. Reduce the following equations into normal form. Find their perpendicular distances from the origin and angle between perpendicular and the positive x-axis.

(i) \(x – \sqrt{3}y + 8 = 0\)

(ii) y – 2 = 0

(iii) x – y = 4

Sol: Based on formulae given in Straight Lines

(i) \(x – \sqrt{3}y + 8 = 0\)

It can be written as:

\(x – \sqrt{3}y = -8\) \(-x + \sqrt{3}y = 8\)

Divide both the sides by \(\sqrt{\left ( -1 \right )^{2} + \left ( \sqrt{3} \right )^{2}}\) = \(\sqrt{4}\) = 2, thus we get,

\(-\frac{x}{2} + \frac{\sqrt{3}}{2}y = \frac{8}{2}\) \(\left (-\frac{1}{2} \right )x + \left (\frac{\sqrt{3}}{2} \right )y = 4\)

\(x\cos 120^{\circ} + y\sin 120^{\circ} = 4\) ————– (1)

Equation (1) is in normal form.

On comparing equation (1) with the normal form of equation of line\(x\cos \omega + y\sin \omega = p\),

Where \(\omega = 120^{\circ}\) and p = 4.

Therefore, the perpendicular distance of the line from the origin is 4, while the angle between the perpendicular and the positive x-axis is \(120^{\circ}\).

(ii) y – 2 = 0

It can be written as:

0.x + 1.y = 2

Divide both the sides by \(\sqrt{\left ( 0\right )^{2} + \left ( 1 \right )^{2}}\) = 1, we obtain 0.x + 1.y = 2

\(x \cos 90^{\circ} + y \sin 90^{\circ} = 2\) ————- (1)

Equation (1) is in normal form.

On comparing equation (1) with the normal form of equation of line\(x\cos \omega + y\sin \omega = p\),

Where \(\omega = 90^{\circ}\) and p = 2.

Therefore, the perpendicular distance of the line from the origin is 2, while the angle between the perpendicular and the positive x-axis is \(90^{\circ}\).

(iii) x – y = 4

It can be written as:

1.x + (-1)y = 4

Divide both the sides by \(\sqrt{\left ( 1 \right )^{2} + \left ( -1 \right )^{2}} = \sqrt{2}\), we obtain,

\(\frac{1}{\sqrt{2}}x + \left ( -\frac{1}{\sqrt{2}} \right )y = \frac{4}{\sqrt{2}}\) \(x \cos \left ( 2\pi – \frac{\pi }{4} \right ) + y \sin \left ( 2\pi – \frac{\pi }{4} \right ) = 2\sqrt{2}\)

\(x \cos 315^{\circ} + y \sin 315^{\circ} = 2\sqrt{2}\) ————– (1)

Equation (1) is in normal form.

On comparing equation (1) with the normal form of equation of line\(x\cos \omega + y\sin \omega = p\),

Where \(\omega = 315^{\circ}\) and p = \(2\sqrt{2}\).

Therefore, the perpendicular distance of the line from the origin is \(2\sqrt{2}\), while the angle between the perpendicular and the positive x-axis is \(315^{\circ}\).

 

 

Q4. Find the distance of the point (–1, 1) from the line 12(x + 6) = 5(y – 2).

Sol: Based on formulae given in Straight Lines

The given equation of the line is 12(x + 6) = 5(y – 2).

12x + 72 = 5y – 10

12x – 5y + 82 = 0 —————- (1)

On comparing equation (1) with general equation of line Ax + By + C = 0, we obtain A = 12, B = –5, and C = 82.

It is known that the perpendicular distance (d) of a line Ax + By + C = 0 from a point \(\left (x_{1}, y_{1} \right )\) is given by,

\(d = \frac{\left | Ax_{1} + By_{1} + C \right |}{\sqrt{A^{2} + B^{2}}}\)

The point is \(\left (x_{1}, y_{1} \right )\) = (-1, 1).

Hence, the distance of point (-1, 1) from the given line is,

= \(\frac{\left | 12\left ( -1 \right ) + \left ( -5 \right )\left ( 1 \right ) + 82\right |}{\sqrt{\left (12 \right )^{2} + \left (-5 \right )^{2}}}\) units

= \(\frac{\left | -12 – 5 + 82\right |}{\sqrt{169}}\) units

= \(\frac{\left | 65\right |}{13}\) units

= 5 units

Q5. Find the points on the x-axis, whose distances from the line \(\frac{x}{3} + \frac{y}{4} = 1\) are 4 units.

Sol: Based on formulae given in Straight Lines

The equation is,

\(\frac{x}{3} + \frac{y}{4} = 1\)

OR

4x + 3y – 12 = 0 ————— (1)

On comparing equation (1) with general equation of line Ax + By + C = 0, we obtain A = 4, B = 3 and C = -12.

Let (p, 0) be the point on the x – axis whose distance from the given line is 4 units.

It is known that the perpendicular distance (d) of a line Ax + By + C = 0 from a point\(\left (x_{1}, y_{1} \right )\) is given by,

\(d = \frac{\left | Ax_{1} + By_{1} + C \right |}{\sqrt{A^{2} + B^{2}}}\) \(4 = \frac{\left | 4p + 3 \times 0 – 12 \right |}{\sqrt{4^{2} + 3^{2}}}\) \(4 = \frac{\left | 4p – 12 \right |}{5}\) \({\left | 4p – 12 \right |} = 20\) \(\pm \left ( 4p – 12 \right ) = 20\)

\(\left ( 4p – 12 \right ) = 20\) OR \(-\left ( 4p – 12 \right ) = 20\)

\(4p = 20 + 12\) OR \(4p = -20 + 12\)

\(p = 8 \; OR \; -2\)

Therefore, the required points on the x-axis are (8, 0) and (–2, 0).

 

 

Q6. Find the distance between parallel lines

(i) 15x + 8y – 34 = 0 and 15x + 8y + 31 = 0

(ii) l (x + y) + p = 0 and l (x + y) – r = 0

Sol: Based on formulae given in Straight Lines

It is known that the distance (d) between parallel lines Ax + By + C₁ = 0 and Ax + By + C₂ = 0 is given by,

\(d = \frac{\left | C_{1} – C_{2}\right |}{\sqrt{A^{2} + B^{2}}}\)

(i) The given parallel lines are 15x + 8y – 34 = 0 and 15x + 8y + 31 = 0.

A = 15

B = 8

\(C_{1}\)= – 34

\(C_{2}\) = 31

Therefore, the distance is,

\(d = \frac{\left | C_{1} – C_{2}\right |}{\sqrt{A^{2} + B^{2}}}\)

= \(\frac{\left | – 34 – 31\right |}{\sqrt{\left (15 \right )^{2} + \left (8 \right )^{2}}}\) units

= \(\frac{\left | – 65\right |}{17}\) units

= \(\frac{65}{17}\) units

(ii) The given parallel lines are l (x + y) + p = 0 and l (x + y) – r = 0

lx + ly + p = 0 and lx + ly – r = 0

Here,

A = l

B = l

\(C_{1}\) = p

\(C_{2}\) = – r

Therefore, the distance is,

\(d = \frac{\left | C_{1} – C_{2}\right |}{\sqrt{A^{2} + B^{2}}}\)

= \(\frac{\left | p + r\right |}{\sqrt{l^{2} + l^{2}}}\) units

= \(\frac{\left | p + r\right |}{\sqrt{2 \; l^{2}}}\) units

= \(\frac{\left | p + r\right |}{l \; \sqrt{2}}\) units

= \(\frac{1}{\sqrt{2}}\frac{\left | p + r\right |}{l}\) units

Q7. Find equation of the line parallel to the line 3x – 4y + 2 = 0 and passing through the point (–2, 3).

Sol: Based on formulae given in Straight Lines

The given equation is,

3x – 4y + 2 = 0

OR

\(b = \frac{3x}{4} + \frac{2}{4}\)

OR

\(b = \frac{3}{4}x + \frac{1}{2}\)

which is of the form y = mx + c

Therefore, slope of the given line = \(\frac{3}{4}\)

We know that parallel lines have the same slope.

Therefore, slope of the other line = m = \(\frac{3}{4}\)

The equation of the line that has a slope of \(\frac{3}{4}\) and passes through the point (-2, 3) is,

\(\left (y – 3 \right ) = \frac{3}{4}\left \{ x – \left ( -2 \right ) \right \}\) \(4y – 12 = 3x + 6\) \(3x – 4y + 18 = 0\)

 

 

Q8. Give equation of the line perpendicular to the line x – 7y + 5 = 0 and having x intercept3.

Sol: Based on formulae given in Straight Lines

The given equation of line is x – 7y + 5 = 0.

\(y = \frac{1}{7}x + \frac{5}{7}\)

which is of the form y = mx + c.

Therefore, slope of the given line = \(\frac{1}{7}\)

The slope of the line perpendicular to the line having a slope of \(\frac{1}{7}\) is,

\(m = – \frac{1}{\left (\frac{1}{7} \right )} = -7\)

The equation of the line with slope –7 and x-intercept 3 is given by,

y = m (x – d)

y = -7 (x – 3)

y = -7 x + 21

7 x + y = 21

 

 

Q9. Calculate angles between the lines\(\sqrt{3}x + y = 1\) and \(x + \sqrt{3}y = 1\).

Sol: Based on formulae given in Straight Lines

The lines are,

\(\sqrt{3}x + y = 1\) and \(x + \sqrt{3}y = 1\)

\(y = – \sqrt{3}x + 1\) ———— (1)

\(y = – \frac{1}{\sqrt{3}x} + \frac{1}{\sqrt{3}}\) —————- (2)

The slope of line (1) is\(m_{1} = -\sqrt{3}\), while the slope of line (2) is \(m_{2} = -\frac{1}{\sqrt{3}}\).

The acute angle \(\theta\) between the two lines is given as:

\(\tan \theta = \left | \frac{m_{1} -m_{2}}{1 + m_{1}m_{2}} \right |\) \(\tan \theta = \left | \frac{-\sqrt{3} + \frac{1}{\sqrt{3}}}{1 + \left ( – \sqrt{3} \right )\left ( – \frac{1}{\sqrt{3}} \right )} \right |\) \(\tan \theta = \left | \frac{\frac{-3 + 1}{\sqrt{3}}}{1 + 1}\right |\) \(\tan \theta = \left | \frac{-2}{2 \times \sqrt{3}}\right |\) \(\tan \theta = \frac{1}{\sqrt{3}}\) \(\theta = 30^{\circ}\)

Therefore, the angle between the given lines is either\(30^{\circ}\) or \(180^{\circ}\) – \(30^{\circ}\) = \(150^{\circ}\)

 

 

Q10. A line passes through points (k, 3)(4, 1) intersects the line 7x – 9y – 19 = 0, at right angle. Find the value of k.

Answer: Based on formulae given in Straight Lines

Given,

Slope passing through points (k, 3) (4, 1)

\(m_{a} = \frac{1 – 3}{4 – k} = \frac{- 2}{4 – k} \\ The \;line\; \\ 7x – 9y – 19 = 0 \\ or, y = \frac{7}{9} x – \frac{19}{9} is\; m_{b} = \frac{7}{9} \\ Lines\; are\; \perp\;ler \\ m_{a} \times m_{b} = – 1 \\ (\frac{- 2}{4 – k}) \times (\frac{7}{9}) = – 1 \\ \frac{- 14}{36 – 9k} = – 1 \\ 14 = 36 – 9 k \\ 9 k = 36 – 14 \\ k = \frac{22}{9}\)

 

 

Q11. Prove that the line through the point (x_a, y_a) and parallel to the line Ax + By + C = 0 is A(x – x_a) + B (y – y_a) = 0.

Answer: Based on formulae given in Straight Lines

The slope of line Ax + By + C = 0

It is known that parallel lines have the same slope.

Slope of the other line = m = \(y = (\frac{- A}{B}) x + (\frac{- C}{B}) \\ m = (- \frac{A}{B}) \\\)

The equation of the line passing through point (x_a, y_a) and having a slope\(m = (- \frac{A}{B}) \\\)

\(y – y_{a} = m (x – x_{a}) \\ y – y_{a} = – \frac{A}{B} (x – x_{a}) \\ B (y – y_{a}) = – A (x – x_{a}) \\ A (x – x_{a}) + B (y – y_{a}) = 0\)

Hence, the line through point (x_a, y_a) and parallel to line Ax + By + C = 0 is \(A (x – x_{a}) + B (y – y_{a}) = 0\)

 

 

Q12. The angle between the two lines is 60° at intersection and passes through the point (2, 3). Obtain the slope of a second line when the slope of first line is 2.

Answer: Based on formulae given in Straight Lines

Given,

Suppose, the slope of 1^st line, m_a = 2.

Then, let the slope of the 2^nd line be m_b.

The lines intersect

\(tan 60^{\circ} = \left | \frac{m_{a} – m_{b}}{1 + m_{a} m_{b}} \right | \\ \sqrt{3} = \left | \frac{m_{a} – m_{b}}{1 + m_{a} m_{b}} \right | \\ \sqrt{3} = \left | \frac{2 – m_{b}}{1 + 2 m_{b}} \right | \\ \sqrt{3} = \pm \frac{2 – m_{b}}{1 + 2 m_{b}} \\ \sqrt{3} = \frac{2 – m_{b}}{1 + 2 m_{b}}\; or\; \sqrt{3} = -\frac{2 – m_{b}}{1 + 2 m_{b}}\; \\ \sqrt{3} (1 + 2 m_{b}) = (2 – m_{b})\; or \;\sqrt{3} (1 + 2 m_{b}) = – (2 – m_{b}) \\ \sqrt{3} + 2 \sqrt{3} m_{b} + m_{b} = 2\; or \;\sqrt{3} + 2 \sqrt{3} m_{b} + m_{b} = – 2\; \\ m_{b} = \frac{2 – \sqrt{3}}{2 \sqrt{3} + 1} \;or\; m_{b} = \frac{- (2 + \sqrt{3})}{2 \sqrt{3} – 1}\)

Case 1: \(m_{b} = \frac{2 – \sqrt{3}}{2 \sqrt{3} + 1}\)

\((y – 3) = \frac{2 – \sqrt{3}}{2 \sqrt{3} + 1}(x – 2) \\ (2 \sqrt{3} + 1)y – 3 (2 \sqrt{3} + 1) = (2 – \sqrt{3}) x – 2 (2 – \sqrt{3}) \\ (\sqrt{3} – 2) x + (2 \sqrt{3} + 1)y = – 4 + 2 \sqrt{3} + 6 \sqrt{3} + 3 \\ (\sqrt{3} – 2) x + (2 \sqrt{3} + 1)y = – 1 + 8 \sqrt{3}\) \((\sqrt{3} – 2) p + (2 \sqrt{3} + 1)q = – 1 + 8 \sqrt{3}\)

Case II :

\(m_{b} = \frac{- (2 + \sqrt{3})}{2 \sqrt{3} – 1} \\ (y – 3) = \frac{- (2 + \sqrt{3})}{2 \sqrt{3} – 1}(p – 2) \\ (2 \sqrt{3} – 1)y – 3 (2 \sqrt{3} – 1) = – (2 + \sqrt{3}) x – 2 (2 + \sqrt{3}) \\ (2 \sqrt{3} – 1)y + (2 + \sqrt{3}) x = 4 + 2 \sqrt{3} + 6 \sqrt{3} – 3 \\ (2 \sqrt{3} – 1)y + (2 + \sqrt{3}) x = 1 + 8 \sqrt{3} \\ (2 + \sqrt{3})x + (2 \sqrt{3} – 1)y = 1 + 8 \sqrt{3}\)

1. \((2 + \sqrt{3})x + (2 \sqrt{3} – 1) y = 1 + 8 \sqrt{3}\)
2. \((\sqrt{3} – 2)x + (2 \sqrt{3} + 1) y = – 1 + 8 \sqrt{3} \; or \; \\ (2 + \sqrt{3})x + (2 \sqrt{3} – 1) y = 1 + 8 \sqrt{3}\)

 

 

Q13 A line segment joining the points (4, 5) and (– 2, 3). Obtain the equation of the perpendicular bisector of the line segment.

Answer Based on formulae given in Straight Lines

Given,

Line segment is bisected at 90^o.

Suppose, the two extreme -points of the line be P (4, 5) and Q (–2, 3)

Mid – point of PQ = \((\frac{4 – 2}{2}, \frac{5 + 3}{2}) = (\frac{2}{2}, \frac{8}{2}) = (1, 4)\)

Slope of PQ = \(\frac{y_{2} – y_{1}}{x_{2} – x_{1}} = \frac{3 – 5}{- 2 – 4} = \frac{- 2}{- 6} = \frac{1}{3}\)

Slope of the line right angled to PQ =\(– \frac{1}{(\frac{1}{3})} = – 3\)

The equation of the line PQ passing through (1, 4) and having a slope of – 3 is

(y – 4) = – 3 (x – 1)

y – 4= – 3 x + 3

3 x + y = 7

Hence, the required equation of the line is 3 x + y = 7

 

 

Q14: Obtain the coordinates of the foot of perpendicular from the point (– 2, 4) to the line 3x – 4y – 16 = 0.

Answer: Let (r, s) be the coordinates of the foot of the perpendicular from the point (–2, 4) to the line 3 x – 4 xy – 16 = 0.

Slope of the line joining (–2, 4) and (r, s),

\(m_{a} =\frac{y_{2} – y_{1}}{x_{2} – x_{1}} = \frac{s – 4}{r + 2}\)

Slope of the line 3x – 4y – 16 = 0 or,

\(y = \frac{3}{4} x – 4 , \\ Here, m_{b} = \frac{3}{4}\)

As we know, if two lines are perpendicular to each other, then

m_am_b = –1

\(\frac{s – 4}{r + 2} \times (\frac{3}{4}) = – 1\\ \frac{3 s – 12}{4 r + 8} = – 1 \\ 3 s – 12 = – (4 r + 8) \\ 3 s – 12 = – 4 r – 8 \\ 4 r + 3 s – 12 + 8 = 0 \\ 4 r + 3 s – 4 = 0\; \; \; …. (1)\)

Point (r, s) lies on line 3 x – 4 y = 16.

3 r – 4 s = 16 … (2)

On solving (1) and (2), we get:

s = –\(\frac{36}{25}\), and

r = \(\frac{64}{25}\)

Hence, the required coordinates of the foot of the perpendicular are \((\frac{64}{25}, – \frac{36}{25})\).

 

 

Q15: The normal meets point (– 2, 3), is drawn from the origin to the equation of line y = m x + c.Obtain the values of m and c.

Answer Based on formulae given in Straight Lines:

Given,

Equation of line is y = m x + c.

Normal drawn from the origin meets point (– 2, 3) of the given line.

Since the line joining the points from origin i.e., (0, 0) and (– 2, 3) is normal to the given line.

Slope of the line joining (0, 0) and (– 2, 3) = \(m_{b} =\frac{y_{2} – y_{1}}{x_{2} – x_{1}} = \frac{3 – 0}{- 2 – 0} = \frac{3}{- 2}\)

Slope of the existing line is as follows,

m_a x m_b = – 1

\(m_{a} \times – \frac{3}{2} = – 1 \\ m_{a} = \frac{2}{3}\)

As the point (– 2, 3) lies on the given line, it satisfies the equation y = m x + c.

3 = m_a (- 2) + c

\(3 = \frac{2}{3} (- 2) + c \\ 3 = \frac{- 4}{3} + c \\ c = 3 + \frac{4}{3} \\ c = \frac{13}{3}\)

Hence, m = \(\frac{2}{3}\) and c = \(\frac{13}{3}\) are the required values.

Q16: Suppose r and s are the lengths from the lines x cos θ – y sin θ = n cos 2θ and x sec θ + y cosec θ = n to the origin perpendiculars, respectively, prove that r ² + 4 s² = n ²

Answer: Based on formulae given in Straight Lines

The equations of both the lines are as follows

x cos θ – y sin θ = n cos 2θ ……. (1)

And,

x sec θ + y cosec θ = n …… (2)

The perpendicular distance (d) of a line A x + B y + C = 0 from a point (x_a, y_a) is given by

\(d = \frac{\left | A x_{a} + B y_{a} + C \right |}{\sqrt{A^{2 + B^{2}}}}\)

Estimating equation (1) to the general equation of line i.e., A x + B y + C = 0, we get, A = cosθ, B = –sinθ, and C = – ncos 2θ.

Given, that r is the length from line (1) to the perpendicular from origin (0, 0).

\(r = \frac{\left | A (0) + B (0) + C \right |}{\sqrt{A^{2}+ B^{2}}} = \frac{\left | C \right |}{\sqrt{A^{2} + B^{2}}} = \frac{\left | – n cos 2\Theta \right |}{\sqrt{cos^{2} \Theta + sin^{2} \Theta }} = \left | – n cos 2\Theta \right |\) ….. (3)

Estimating equation (1) to the general equation of line i.e., A x + B y + C = 0, we get, A = secθ, B = cosecθ, and C = – n.

Also given, that s is the length from line (2) to the perpendicular from origin (0, 0)

\(s = \frac{\left | A (0) + B (0) + C \right |}{\sqrt{A^{2}+ B^{2}}} = \frac{\left | C \right |}{\sqrt{A^{2} + B^{2}}} = \frac{\left | – n \right |}{\sqrt{sec^{2} \Theta + cosec^{2} \Theta }}\) …… (4)

From (3) and (4), we have

r ² + 4 s² = n ²

\(r^{2} + 4 s^{2} = (\left | – n cos 2\Theta \right |)^{2} + 4 (\frac{\left | – n \right |}{\sqrt{sec^{2} \Theta + cosec^{2} \Theta }} )^{2} \\ = n^{2} cos^{2} 2\Theta + \frac{4 n^{2}}{sec^{2} \Theta + cosec^{2} \Theta} \\ = n^{2} cos^{2} 2\Theta + \frac{4 n^{2}}{\frac{1}{cos^{2} \Theta } + \frac{1}{sin^{2} \Theta }} \\ = n^{2} cos^{2} 2\Theta + \frac{4 n^{2}}{\frac{cos^{2} \Theta + sin^{2} \Theta }{cos^{2} \Theta sin^{2} \Theta }} \\ = n^{2} cos^{2} 2\Theta + \frac{4 n^{2}}{\frac{1}{cos^{2} \Theta sin^{2} \Theta}} \\ = n^{2} cos^{2} 2\Theta + 4 n^{2}cos^{2} \Theta sin^{2} \Theta \\ = n^{2} cos^{2} 2\Theta + n^{2}(2 cos \Theta sin \Theta)^{2} \\ = n^{2} cos^{2} 2\Theta + n^{2} sin^{2} 2\Theta \\ = n^{2}\)

Hence proved

 

 

Q17: The vertices of the triangle PQR are P (3, 4), Q (5, – 2) and R (2, 3), obtain how long the altitude is from the vertex P and also obtain the equation.

Answer:

Assume, the altitude is PS from triangle PQR to vertex P

Correspondingly,

\(PS \perp QR\)

The equation as the line passes through the point (3, 4) and having 1 as its slope

(y – 4) = 1(x – 3)

⇒ x – y + 1 = 0

⇒ y – x = 1

Altitude’s equation for vertex P is

l – k= 1.

Length of PS = Length of the normal from QR to P (3, 4)

The equation of QR is

\((y + 2) = \frac{3 + 2}{2 – 5} (x – 5) \\ (y + 2) = \frac{5}{- 3} (x – 5) \\ – 3 y – 6 = 5 x – 25 \\ 5 x + 3y = 19 \\ 5 x + 3 y – 19 = 0 \\\)

The perpendicular distance (d) of a line A x + B y + C = 0 from a point (x_a, y_a) is given by

\(d = \frac{\left | A x_{a} + B y_{a} + C \right |}{\sqrt{A^{2 + B^{2}}}}\)

Estimating equation (1) to the general equation of line i.e., A x + B y + C = 0, we get,

A = 5, B = 3, and C = – 19.

Length of PS = \(y = \frac{\left | 5 (3) + 3 (4) + (- 19) \right |}{\sqrt{5^{2}+ 3^{2}}}\; units = \frac{\left | 8 \right |}{\sqrt{25 + 9}}\; units = \frac{\left | 8 \right |}{\sqrt{34}} \; units\)

 

 

Q 18: Suppose ‘r’ is the length of the origin to the line from perpendicular from the normal. The line has axes i and j axes as intercepts of the line, then prove that:

\(\frac{1}{r ^{2}} = \frac{1}{i ^{2}} + \frac{1}{j ^{2}}\)

Answer: Based on formulae given in Straight Lines

The line has axes i and j axes as intercepts of the line and its equation is

\(\frac{x}{i} + \frac{y}{j} = 1 \\\)

\(\Rightarrow\) \(jx + yi = ij \\\)

\(jx + yi – ij = 0 \\\) …… (1)

To prove: \(\frac{1}{r ^{2}} = \frac{1}{i ^{2}} + \frac{1}{j ^{2}}\)

The perpendicular distance (d) of a line A k + B l + C = 0 from a point (k₁, l₁) is given by

\(d = \frac{\left | A k_{1} + B l_{1} + C \right |}{\sqrt{A^{2 + B^{2}}}}\)

Estimating equation (1) to the general equation of line i.e., A x + B y + C = 0, we get,

A = j, B = i, and C = –ij

Also given, that r is the length from line (1) to the length of a perpendicular from origin (0, 0) , we get

\(r = \frac{\left | A (0) + B (0) – ij \right |}{\sqrt{i^{2}+ j^{2}}} \\ r = \frac{\left | – ij \right |}{\sqrt{i^{2}+ j^{2}}} \\ Square\; on\; both\; the\; sides\; \\ r^{2} = \frac{(- ij) ^{2}}{i^{2}+ j^{2}} \\ r^{2} (i^{2}+ j^{2}) = i^{2} j^{2} \\ \frac{i^{2}+ j^{2}}{i^{2} j^{2}} = \frac{1}{ r^{2}} \\ \frac{1}{i ^{2}} + \frac{1}{j ^{2}} = \frac{1}{r ^{2}}\).

Hence proved

Previous

Next