NCERT Class 12 Chapter – 8: Application of Integrals

 

Area between two curves: Based on formula given in Application of Integrals

CASE – 1:

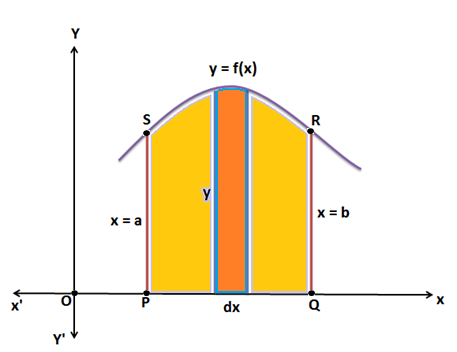
For finding the Area bounded by the curve y = f(x), x-axis and the lines x = a, x = b let us consider a very thin vertical strip of length y and width dx. Therefore, Area of the strip (dA) = y dx [Since, y = f(x)]

Hence the total Area enclosed by the curve y = f(x), x- axis and the lines x = a, x = b:

\(\boldsymbol{A =\int_{a}^{b} dA=\int_{a}^{b}y\;dx}\)

Therefore, A = \(\int_{a}^{b}f(x)\;dx\)

CASE – 2:

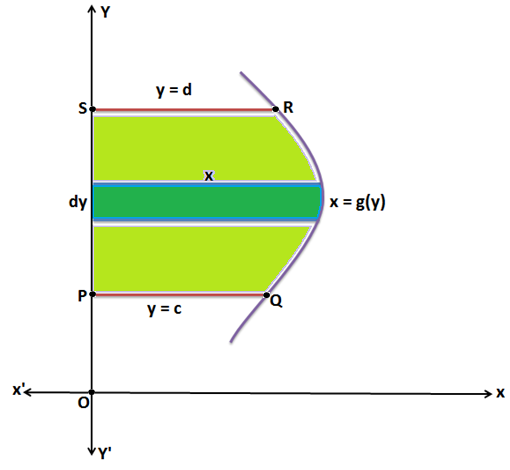
Similarly the Area bounded by the curve x = g(y), y-axis and the lines y = c, y = d is given by:

\(A=\int_{c}^{d} dA=\int_{c}^{d} x\;dy\)

Therefore, A = \(\int_{c}^{d}g(y)\;dy\)

CASE – 3:

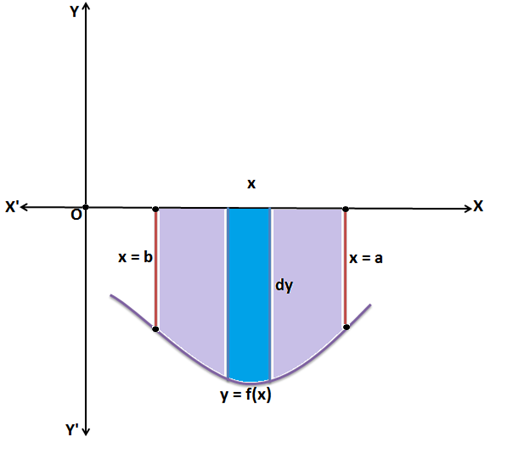
If the curve lies below x-axis, then the Area bounded by the curve y = f(x), x-axis and the lines x = a, x = b will come negative.

Since, the area cannot be negative therefore we will neglect the negative sign and considering its absolute value only.

\(A = \left |\int_{a}^{b}f(x)\;dx \right|\)

CASE – 4:

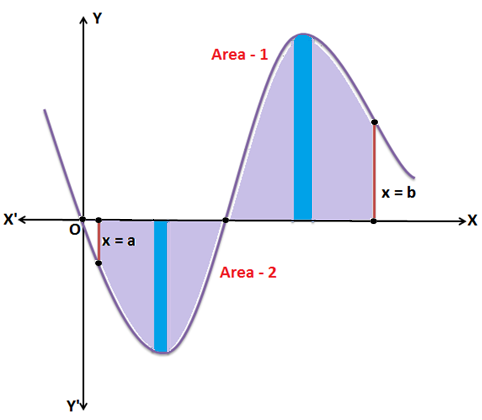
As shown above, some portion of the curve lies above the x-axis and some portion of the curve lies below the x-axis.

Here in this case, Area-1 > 0 and Area-2 < 0

Therefore, total Area bounded by the curve y= f(x), x-axis and the lines x=a, x=b is given by: A = |A|+B

NOTE:

\(\boldsymbol{\int \sqrt{a^{2}-x^{2}}\;dx = \frac{x}{2}\sqrt{a^{2}-x^{2}}+\frac{a^{2}}{2}\sin^{-1}\frac{x}{a}}\)

Example 1: Find the area enclosed by equation: x² + y² = 9

Sol:Based on formula given in Application of Integrals

Equation x² + y² = 3² represents the circle with centre (0,0) and radius 3 units.

Therefore, y = \(\sqrt{3^{2}-x^{2}}\)

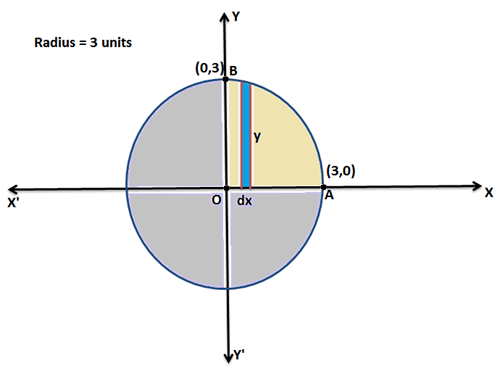
From the figure, the Area enclosed by the circle = 4 × (Area enclosed by the curve ABOA)

Now, Area enclosed by the curve ABOA:

\(\boldsymbol{\Rightarrow }\) \(\int_{0}^{3}y\;dx = \int_{0}^{3} \sqrt{9-x^{2}}\;dx\)

Since, \(\\\int \sqrt{a^{2}-x^{2}}\;dx = \frac{x}{2}\sqrt{a^{2}-x^{2}}+\frac{a^{2}}{2}\sin^{-1}\frac{x}{a}\)

\(\\\boldsymbol{\Rightarrow }\) \(\boldsymbol{\int_{0}^{3}\sqrt{3^{2}-x^{2}}\;dx=\left | \frac{x}{2} \sqrt{9-x^{2}}+\frac{9}{2} \sin^{-1}\frac{x}{3} \right | _{0}^{3}}\\\)

\(\\\boldsymbol{\Rightarrow }\) \(\boldsymbol{\frac{3}{2} \sqrt{9-9}+\frac{9}{2} \sin^{-1}(1) – \frac{0}{2} \sqrt{9-0}-\frac{0}{2} \sin^{-1}\frac{0}{3}}\\\)

\(\\\boldsymbol{\Rightarrow }\) \(\boldsymbol{\frac{9}{2}\times \frac{\pi }{2}=\frac{9\pi }{4}}\) unit²

Therefore, the Area enclosed by the circle = 4 × (area enclosed by curve ABOA)

\(\boldsymbol{\Rightarrow }\) \(4\times \frac{9\pi }{4}=9\pi\)

Hence the Area enclosed by the circle = 9π unit²

 

 

Example 2: Find the area enclosed by the curve \(\frac{x^{2}}{9}+\frac{y^{2}}{4} = 1\)

Sol:Based on formula given in Application of Integrals

Equation \(\frac{x^{2}}{9}+\frac{y^{2}}{4} = 1\) represents an ellipse with major axis = 3 units and minor axis = 2 units

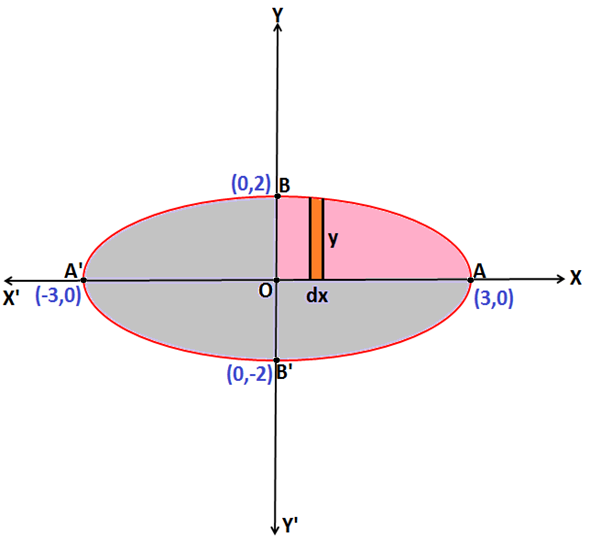Since, \(\frac{x^{2}}{9}+\frac{y^{2}}{4} = 1\)

\(\boldsymbol{\Rightarrow }\) 4x² + 9y² = 36

\(\boldsymbol{\Rightarrow }\) 9y² = 6² – (2x)²

Therefore, \(y=\sqrt{\frac{6^{2}-(2x)^{2}}{9}}\)

Therefore, the Area of region enclosed by the ellipse = 4 × (Area enclosed by the curve ABOA)

Now, Area enclosed by the curve ABOA = \(\int_{0}^{3} y\;dx\)

Since, \(\int \sqrt{a^{2}-x^{2}}\;dx = \frac{x}{2}\sqrt{a^{2}-x^{2}}+\frac{a^{2}}{2}\sin^{-1}\frac{x}{a}\)

\(\\\boldsymbol{\Rightarrow }\) \(\boldsymbol{\frac{1}{3}\times \int_{0}^{3}\sqrt{6^{2}-(2x)^{2}}}\\\)

\(\\\boldsymbol{\Rightarrow }\) \(\boldsymbol{\frac{1}{3}\int_{0}^{3}\;\frac{2x}{2}\sqrt{6^{2}-(2x)^{2}}+\frac{36}{2}\sin^{-1}\frac{2x}{6}}\\\)

\(\\\boldsymbol{\Rightarrow }\) \(\boldsymbol{\frac{1}{3}\left | \frac{2x}{2}\sqrt{6^{2}-(2x)^{2}}+\frac{36}{2}\sin^{-1}\frac{2x}{6} \right |_{0}^{3}}\\\)

\(\\\boldsymbol{\Rightarrow }\) \(\boldsymbol{\frac{1}{3}[\frac{6}{2}\sqrt{36-36}+18\sin^{-1}(1)]=3\pi }\)

Therefore, the Area enclosed by the curve ABOA = 3π unit²

Hence, the total Area enclosed by an ellipse ABA’B’ = 4×3π = 12π unit².

Area of region bounded by the curve and line:

Example 3: Find the area of the region enclosed by the curve y = x² and the line y = 3.

Sol: Based on formula given in Application of Integrals

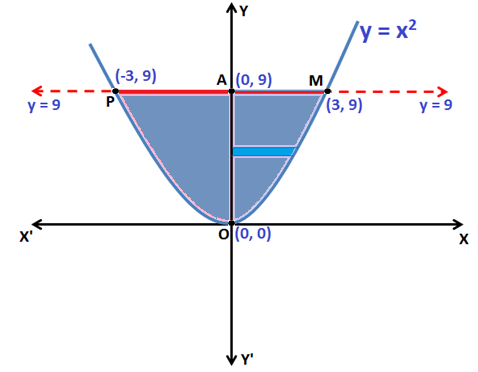
y = x² represents a parabola, symmetrical about y-axis as shown in the above figure. By substituting y =9 in equation of parabola y = x² we will get coordinates of point M.

i.e. x² = 9

Therefore, x = +3 or -3

Hence the coordinates of point M = (3, 9)

The area of the region bounded by the curve y = x² and the line y = 9 is the area enclosed by curve POMP.

Now, Area of region POMP = 2(area of region AOMA)

Since, x² = y

Therefore, x = \(\sqrt{y}\)

Thus, the Area of region bounded by the curve AOMA:

\(\boldsymbol{\Rightarrow }\) \(\int_{0}^{9}x\;dy\) = \(\int_{0}^{9}\sqrt{y}\;dy\)

\(\boldsymbol{\Rightarrow }\) \(\boldsymbol{{\left | \frac{2}{3}\times (y)^{\frac{3}{2}} \right |_{0}^{9}=\frac{2}{3}\times (9^{\frac{3}{2}})}}\\\)

\(\boldsymbol{\Rightarrow }\) \(\boldsymbol{\frac{2}{3}\times 27 = 18}\)unit²

Therefore, the Area of region bounded by the curve AOMA = 18 unit²

Hence, the Area of region bounded by the curve POMP = 2 × (area of region bounded by curve AOMA) = 36 unit²

Example 4: Find the area enclosed by the curve x² + y² = 50, x-axis and the line y = x in the 1^st quadrant.

Sol: Based on formula given in Application of Integrals

Equation x² + y² = 50 represents a circle with radius \(\sqrt{50}\) units.

Since y = x

Therefore x² + x² = 50 [for points of intersection of both the curves]

Hence, x = +5 and -5

Similarly, y = +5 and -5

Thus the coordinates of point B are (5, 5)

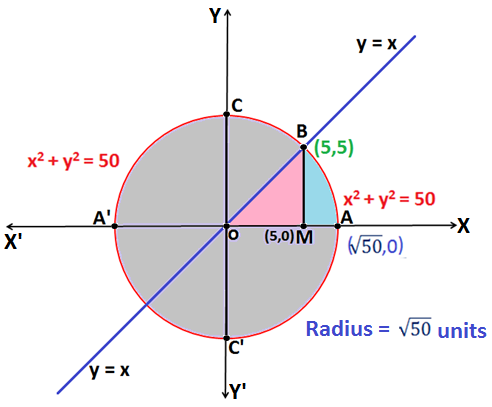
Form the figure, the area of region bounded by the curve x² + y² = 50, x = y and x – axis in the 1^st quadrant is the Area enclosed by the curve OMABO.

i.e. Area of triangle OMB + Area under the curve MBAM.

Now, the Area of triangle = \(\frac{1}{2}\times Base \times Altitude\)

\(\boldsymbol{\Rightarrow }\) \(\frac{1}{2}\times OM \times BM\;\;=\;\frac{1}{2}\times 5\times 5 =\frac{25}{2}\) unit².

Now, the Area under the curve MBAM = \(\int_{5}^{5\sqrt{2}}y\;dx\)

Since, x² +y² = 50. Therefore, y² = 50 – x²

\(\boldsymbol{\Rightarrow }\) \(\boldsymbol{y=\sqrt{50-x^{2}}}\)

Therefore, the Area under curve MBAM [x² + y² = 50]:

Since, \(\\\int \sqrt{a^{2}-x^{2}}\;dx = \frac{x}{2}\sqrt{a^{2}-x^{2}}+\frac{a^{2}}{2}\sin^{-1}\frac{x}{a}\)

\(\\\boldsymbol{\Rightarrow }\) \(\boldsymbol{\int_{5}^{5\sqrt{2}}\sqrt{50-x^{2}}\;dx=\left | \frac{x}{2}\sqrt{50-x^{2}}+\frac{50}{2}\;\sin^{-1}\frac{x}{5\sqrt{2}} \right |_{5}^{5\sqrt{2}}}\\\)

\(\\\boldsymbol{\Rightarrow }\) \(\boldsymbol{[\frac{5\sqrt{2}}{2}\times\ \sqrt{50-50}]+[\frac{50}{2}\;\sin^{-1}(1)]-[\frac{5}{2}\times \sqrt{50-25}]-[\frac{50}{2}\times \sin^{-1}\frac{1}{\sqrt{2}}]}\\\)

\(\\\boldsymbol{\Rightarrow }\) \(\boldsymbol{0+\frac{25\pi }{2}-\frac{25}{2}-\frac{25\pi }{4}=\frac{25}{4}(\pi -2)}\)unit²

Therefore, the Area under the curve MBAM = \(\boldsymbol{\frac{25}{4}(\pi -2)}\) unit²

Now, the total Area under the shaded region = Area of triangle OMB + Area under the curve MBAM

\(\boldsymbol{\Rightarrow }\) \(\frac{25}{2}+\frac{25}{4}(\pi -2)=\frac{25}{2}+\frac{25\pi }{4}-\frac{25}{2}\boldsymbol{=\frac{25\pi }{4}}\)unit²

Hence, the Area of shaded region OMABO = \(\boldsymbol{\frac{25\pi }{4}}\)unit²

Exercise 8.1

Q.1: Find the area enclosed by the curve y = x² and the lines y = 2, y = 4 and the y-axis.

Sol: Based on formula given in Application of Integrals

Equation y = x² represents a parabola symmetrical about y-axis.

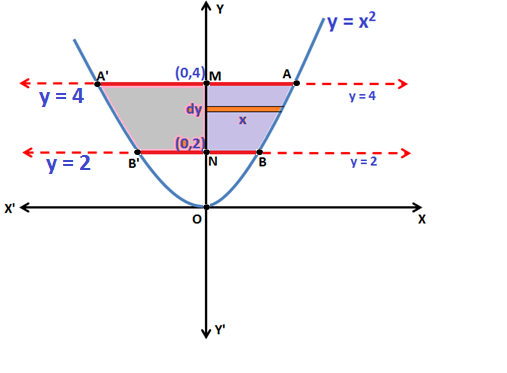
The Area of the region bounded by the curve y = x², y = 2, and y = 4, is the Area enclosed by the curve AA’B’BA.

Now, the Area of region AA’B’BA = 2 (Area of region ABNMA)

Since, x² = y

Therefore, x = \(\sqrt{y}\)

Thus, the Area of region bounded by the curve ABNMA [y = x²]:

\(\boldsymbol{\Rightarrow }\) \(\int_{2}^{4}x\;dy\) = \(\int_{2}^{4}\sqrt{y}\;dy\)

\(\boldsymbol{\Rightarrow }\) \(\boldsymbol{{\left | \frac{2}{3}\times (y)^{\frac{3}{2}} \right |_{2}^{4}=\frac{2}{3}\times [(4^{\frac{3}{2}})-(2)^{\frac{3}{2}}}]}\)

\(\boldsymbol{\Rightarrow }\) \(\boldsymbol{\frac{2}{3}\times (8-2\sqrt{2}) = \frac{4}{3}(4-\sqrt{2})}\) unit²

Therefore, the Area of region bounded by the curve ABNMA = \(\boldsymbol{\frac{4}{3}(4-\sqrt{2})}\)unit²

Hence, the Area of region bounded by the curve AA’B’BA = 2(Area of region bounded by the curve ABNMA)= \(\boldsymbol{\frac{8}{3}(4-\sqrt{2})}\)unit²

 

Q.2: Find the area enclosed by the curve y² = 4x and lines x = 1, x = 3 and the x- axis in the first quadrant.

Sol : Based on formula given in Application of Integrals

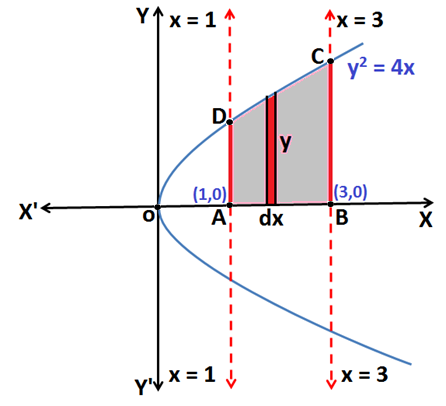
Equation y² = 4x represents a parabola, symmetrical about the x-axis as shown in the above figure.

The area of the region bounded by the curve y² = 4x, x = 1, x = 3 and the x-axis is the area enclosed by the curve ABCDA.

Now, the Area of region bounded by the curve ABCDA:

Since, y² = 4x

Therefore, y = \(2\sqrt{x}\)

Hence, the area of region bounded by the curve ABCDA [y² = 4x]:

\(\boldsymbol{\Rightarrow }\) \(\int_{1}^{3}y\;dx\) = \(\int_{1}^{3}2\sqrt{x}\;dx\)

\(\\\boldsymbol{\Rightarrow }\) \(\boldsymbol{{\left | 2\times \frac{2}{3}\times (x)^{\frac{3}{2}} \right |_{1}^{3}=\frac{4}{3}\times [(3^{\frac{3}{2}})-(1)}]}\)

\(\\\boldsymbol{\Rightarrow }\) \(\boldsymbol{\frac{4}{3}\times (3\sqrt{3}-1) = \frac{-4\;+\;12\sqrt{3}}{3}}\) unit²

Therefore, the area of region bounded by the curve ABCDA \(\boldsymbol{= \frac{-4\;+\;12\sqrt{3}}{3}}\)unit²

Q.3: Find the value of k if the line x = k divides the area enclosed by the curve y² = 9x and the line x = 4 in to two equal parts.

Sol: Based on formula given in Application of Integrals

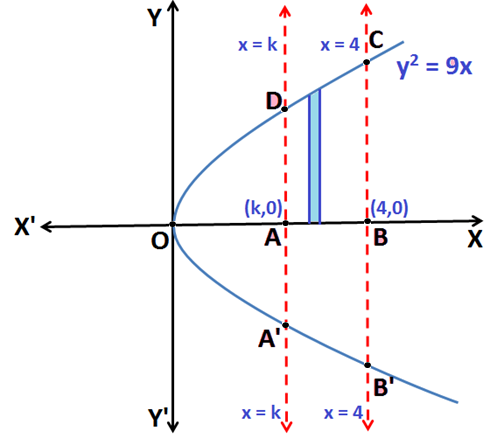
Equation y² = 9x represents a parabola, symmetrical about the x-axis as shown in the above figure.

Since, the line x = k divides the Area OCBB’O in to two equal halves and the curve is symmetrical to x-axis. Therefore, Area of the region OADO = Area of the region ABCDA.

The Area of the region bounded by the curve y² = 9x and the line x = k is the Area of region enclosed by the curve OADO.

Since, y² = 9x

Therefore, y = \(3\sqrt{x}\)

Hence, the Area of region bounded by the curve OADO:

\(\boldsymbol{\Rightarrow }\) \(\int_{0}^{k}y\;dx\) = \(\int_{0}^{k}3\sqrt{x}\;dx\)

\(\\\boldsymbol{\Rightarrow }\) \(\boldsymbol{{\left | 3\times \frac{2}{3}\times (x)^{\frac{3}{2}} \right |_{1}^{3}=2\times [(k^{\frac{3}{2}})-(0)}]}\)

\(\\\boldsymbol{\Rightarrow }\) \(\boldsymbol{2k^{\frac{3}{2}}}\)unit²

Therefore, the Area of region bounded by the curve OADO = \(\boldsymbol{2k^{\frac{3}{2}}}\)unit²

The Area of the region bounded by the curve y² = 9x and the lines x = k and x = 4 is the Area under the curve ABCDA

Now, the Area of region bounded by the curve ABCDA [y² = 9x]:

\(\boldsymbol{\Rightarrow }\) \(\int_{k}^{4}y\;dx\) = \(\int_{k}^{4}3\sqrt{x}\;dx\)

\(\boldsymbol{\Rightarrow }\) \(\boldsymbol{{\left | 3\times \frac{2}{3}\times (x)^{\frac{3}{2}} \right |_{k}^{4}=2\times [(4^{\frac{3}{2}})-(k)^{\frac{3}{2}}}]}\)

\(\boldsymbol{\Rightarrow }\) \(\boldsymbol{(16-2k^{\frac{3}{2}})}\) unit²

Therefore, the Area of region bounded by the curve ABCDA = \(\boldsymbol{\Rightarrow (16-2k^{\frac{3}{2}})}\) unit²

Since, the Area of region OADO = Area of region ABCDA [GIVEN]

\(\\\boldsymbol{\Rightarrow }\) \(\boldsymbol{(16-2k^{\frac{3}{2}})=2k^{\frac{3}{2}}}\)

\(\\\boldsymbol{\Rightarrow }\) \(\boldsymbol{k^{\frac{3}{2}}=4}\)

\(\\\boldsymbol{\Rightarrow }\) \(\boldsymbol{k = 4^{\frac{2}{3}}}\)

Therefore, the value of k = \(\boldsymbol{4^{\frac{2}{3}}}\)

Q.4: Find the area enclosed by the curve y² = 16x, y-axis and the line y = 2.

Sol: Based on formula given in Application of Integrals

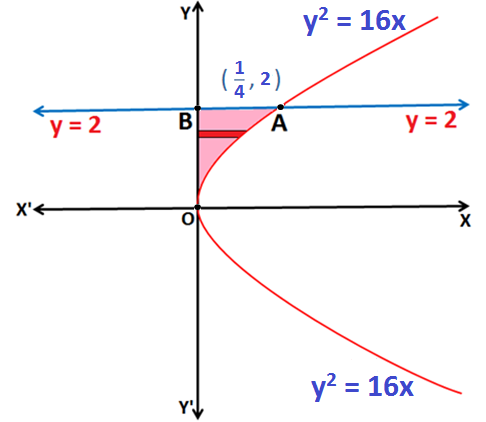
Equation y² = 16x represents a parabola, symmetrical about the x-axis as shown in the above figure.

The Area of the region bounded by the curve y² = 16x, y = 2 and the y-axis is the Area of region enclosed by the curve OABO.

Now, the Area of region enclosed by the curve OABO:

Since, y² = 16x

Therefore, x = \(\frac{y^{2}}{16}\)

Thus, the Area of region bounded by the curve OABO:

\(\\\boldsymbol{\Rightarrow }\) \(\int_{0}^{2}x\;dy\) = \(\int_{0}^{2}\frac{y^{2}}{16}\;dy\)

\(\\\boldsymbol{\Rightarrow }\) \(\boldsymbol{{\left | \frac{1}{16}\times \frac{y^{3}}{3}\right |_{0}^{2}=\frac{1}{16}\times [\frac{8}{3}-0}]}\\\)

\(\\\boldsymbol{\Rightarrow }\) \(\boldsymbol{\frac{1}{6}}\) unit²

Therefore, Area of region bounded by the curve OABO \(\boldsymbol{=\frac{1}{6}}\)unit²

Q.5: Find the area enclosed by the curve y² = 25x and the line x = 3

Sol: Based on formula given in Application of Integrals

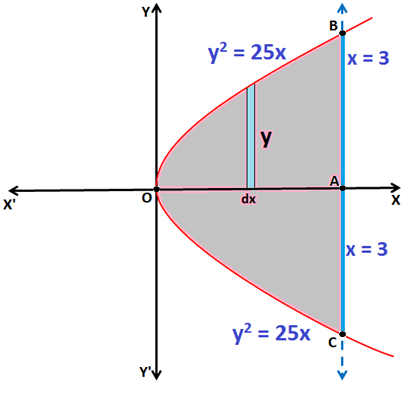
Equation y² = 25x represents a parabola, symmetrical about x-axis as shown in the above figure.

The area of the region bounded by the curve y² = 25x and x = 3 is the Area enclosed by the curve BOCAB.

Now, the Area of region BOCAB = 2(Area of region OABO)

Since, y² = 25x

Therefore, y = \(5\sqrt{x}\)

Hence, the Area of region bounded by the curve OABO:

\(\\\boldsymbol{\Rightarrow }\) \(\int_{0}^{3}y\;dx\) = \(\int_{0}^{3}5\sqrt{x}\;dx\)

\(\\\boldsymbol{\Rightarrow }\) \(\boldsymbol{{\left | 5\times \frac{2}{3}\times (x)^{\frac{3}{2}} \right |_{0}^{3}=\frac{10}{3}\times [(3^{\frac{3}{2}})-(0)}]}\)

\(\\\boldsymbol{\Rightarrow }\) \(\boldsymbol{\frac{10}{3}\times (3\sqrt{3})=10\sqrt{3}}\)unit²

Therefore, the Area of region bounded by the curve OABO\(\boldsymbol{=10\sqrt{3}}\) unit²

Now, the Area of region BOCAB = 2 × (Area of region OABO) \(\boldsymbol{=20\sqrt{3}}\) unit²

Q.6: Find the area enclosed by the curve x² = 8y, y = 1, y = 9 and the y-axis in the first quadrant.

Sol: Based on formula given in Application of Integrals

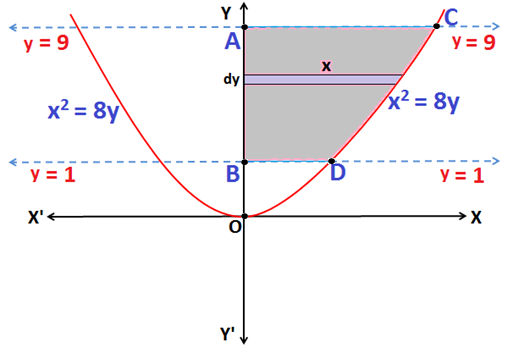
Equation x² = 8y represents a parabola, symmetrical about the y-axis as shown in the above figure.

The area of the region bounded by the curve x² = 8y, y = 1, y = 9 and the first quadrant is the area enclosed by the curve ABDCA.

Now, the Area of the region ABDCA:

Since, x² = 8y

Therefore, x = \(2\sqrt{2y}\)

Hence, the Area of region bounded by the curve ABDCA:

\(\\\boldsymbol{\Rightarrow }\) \(\int_{1}^{9}x\;dy\) = \(\int_{1}^{9}2\sqrt{2y}\;dy\\\)

\(\\\boldsymbol{\Rightarrow }\) \(\boldsymbol{{\left | 2\sqrt{2}\times \frac{2}{3}\times (y)^{\frac{3}{2}} \right |_{1}^{9}=\frac{4\sqrt{2}}{3}\times [(9^{\frac{3}{2}})-(1)}]}\\\)

\(\\\boldsymbol{\Rightarrow }\) \(\boldsymbol{\frac{4\sqrt{2}}{3}\times (27-1)=104\times \frac{\sqrt{2}}{3}}\) unit²

Therefore, Area of region bounded by the curve ABDCA \(\boldsymbol{=104\times \frac{\sqrt{2}}{3}}\)unit²

Q.7: Find the area bounded by the curve whose equation is x² = 9y and the line x = 6y – 3.

Sol: Based on formula given in Application of Integrals

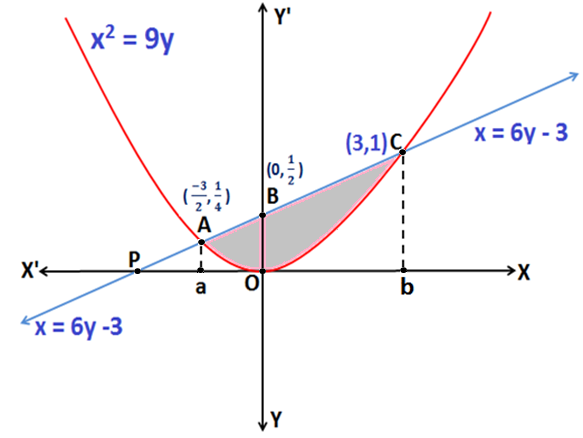
Equation x² = 9y represents a parabola, symmetrical about the y-axis as shown in the above figure.

The Area of the region bounded by parabola x² = 9y and the line x =6y – 3 is the Area enclosed under the curve ABC0A.

Since, the parabola x² = 9y and the line x = 6y – 3 intersect each other at points A and C, hence the coordinates of points A and C are given by:

(6y-3)² = 9y

\(\boldsymbol{\Rightarrow }\) 36y² – 45y + 9 = 0

By Hit and Trial method solutions of this quadratic equation are:

y = 1 and y = \(\frac{1}{4}\)

Hence, the co-ordinates of point A and point C are (3,1) and \((\frac{-3}{2},\frac{1}{4})\) respectively

Since, x² = 9y

Therefore, x = \(3\sqrt{y}\)

The Area of region bounded by the curve ABCOA = [Area of region OBCbO – Area of region OCbO] + [Area of region ABOaA – Area of region OAaO]

The Area enclosed by the curve OBCbO:

\(\\\boldsymbol{\Rightarrow }\) \(\int_{0}^{3} y\;dx = \boldsymbol{\int_{0}^{3}\frac{x+3}{6}\;dx}\)

\(\\\boldsymbol{\Rightarrow }\) \(\boldsymbol{\frac{1}{6}\left | \frac{x^{2}}{2}+ 3x \right |_{0}^{3}}\)

\(\\\boldsymbol{\Rightarrow }\) \(\boldsymbol{\frac{1}{6}(\frac{9}{2}+9)=\frac{9}{4}}\) unit²

The Area enclosed by the curve ABOaA:

\(\\\boldsymbol{\Rightarrow }\) \(\boldsymbol{\int_{\frac{-3}{2}}^{0}\;y\;dx} = \boldsymbol{\int_{\frac{-3}{2}}^{0}\frac{x+3}{6}\;dx}\)

\(\\\boldsymbol{\Rightarrow }\) \(\boldsymbol{\frac{1}{6}\left | \frac{x^{2}}{2}+ 3x \right |_{\frac{-3}{2}}^{0}}\)

\(\\\boldsymbol{\Rightarrow }\) \(\boldsymbol{\frac{1}{6}(0-\frac{9}{8}+\frac{9}{2})=\frac{9}{16}}\) unit²

The Area enclosed by the curve OAaO:

\(\\\boldsymbol{\Rightarrow }\) \(\boldsymbol{\int_{\frac{-3}{2}}^{0}\;y\;dx\; =\;\int_{\frac{-3}{2}}^{0} \frac{x^{2}}{9}\;dx}\)

\(\\\boldsymbol{\Rightarrow }\) \(\boldsymbol{\frac{1}{9}\left | \frac{x^{3}}{3}\right |_{\frac{-3}{2}}^{0}}\)

\(\\\boldsymbol{\Rightarrow }\) \(\boldsymbol{\frac{1}{27}(0-\frac{-27}{8})=\frac{1}{8}}\)unit²

The Area enclosed by the curve OCbO:

\(\\\boldsymbol{\Rightarrow }\) \(\boldsymbol{\int_{0}^{3} y\;dx\; = \;\int_{0}^{3}\frac{x^{2}}{9}\;dx}\)

\(\\\boldsymbol{\Rightarrow }\) \(\boldsymbol{\frac{1}{9}\left | \frac{x^{3}}{3}\right |_{0}^{3}}\)

\(\\\boldsymbol{\Rightarrow }\) \(\boldsymbol{\frac{1}{9}(\frac{27}{3}-0)=1}\) unit²

Since, the Area of region bounded by the curve ABCOA = [Area of region OBCbO – Area of region OCbO] + [Area of region ABOaA – Area of region OAaO]

\(\boldsymbol{\Rightarrow }\) \(\boldsymbol{[\frac{9}{4}-1]+[\frac{9}{16}-\frac{1}{8}]=\frac{27}{16}}\)

Therefore, the Area of region bounded by the curve ABCOA \(=\frac{27}{16}\) unit²

 

 

Q.8: Find the area enclosed by the curve 4y = x² and y = |x|

Sol:Based on formula given in Application of Integrals

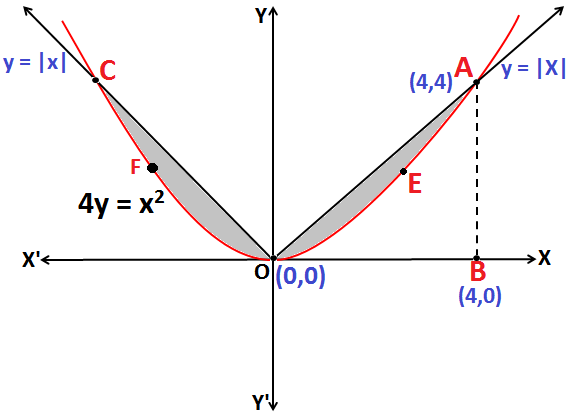
Equation x² = 4y represents a parabola, symmetrical about the y-axis as shown in the above figure.

The area of the region bounded by the curve x² = 4y and y = |x| is 2(OAEO) i.e. (area OCFO+ area OAEO)

Now, Area of region OAEO = OABO – OEABO

Since, x² = 4y

\(\boldsymbol{\Rightarrow }\) \(y=\frac{x^{2}}{4}\)

Now, the Area of region bounded by the curve OEABO:

\(\\\boldsymbol{\Rightarrow }\) \(\boldsymbol{\int_{0}^{4}y\;dx\;=\;\int_{0}^{4}\frac{x^{2}}{4}\;dx}\)

\(\\\boldsymbol{\Rightarrow }\) \(\boldsymbol{\frac{1}{4}\left | \frac{x^{3}}{3} \right |_{0}^{4}=\frac{16}{3}}\) unit²

Therefore, the area of region bounded by the curve OEABO = \(=\frac{16}{3}\) unit²

Now, the Area of region bounded by the curve OABO:

\(\\\boldsymbol{\Rightarrow }\) \(\boldsymbol{\int_{0}^{4}y\;dx\;\Rightarrow \;\int_{0}^{4}x\;dx}\)

\(\\\boldsymbol{\Rightarrow }\) \(\boldsymbol{\left | \frac{x^{2}}{2} \right |_{0}^{4}=8}\) unit²

Therefore, the Area of the region bounded by the curve OABO = 8 unit²

Now, Area of region OAEO = Area of region (OABO – OEABO)

\(\boldsymbol{\Rightarrow }\) \(8-\frac{16}{3}\) = \(\frac{8}{3}\) unit²

Therefore, the total Area of shaded region = 2×\(\frac{8}{3}\) = \(\frac{16}{3}\)unit²

Q.9: Find the area enclosed by the curve \(\frac{x^{2}}{4}+\frac{y^{2}}{9} = 1\)

Sol:Based on formula given in Application of Integrals

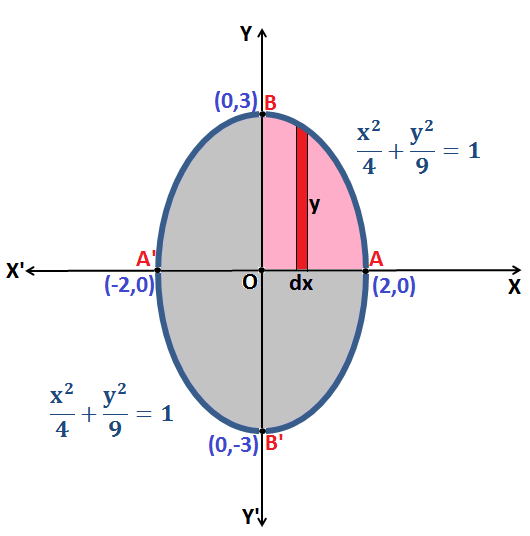
Equation \(\frac{x^{2}}{4}+\frac{y^{2}}{9} = 1\) represents an ellipse.

Since, \(\frac{x^{2}}{4}+\frac{y^{2}}{9} = 1\\\)

\(\\\boldsymbol{\Rightarrow }\) \(\frac{y^{2}}{9}=1-\frac{x^{2}}{4}\\\)

\(\\\boldsymbol{\Rightarrow }\) \(y=\frac{3}{2}\sqrt{4-x^{2}}\)

Therefore, the Area of region enclosed by the ellipse = 4 × (Area enclosed by the curve ABOA)

Now, the Area enclosed by the curve ABOA:

\(\boldsymbol{\Rightarrow }\) \(\boldsymbol{\int_{0}^{2} y\;dx\;=\; \frac{3}{2}\times \int_{0}^{2}\sqrt{2^{2}-(x)^{2}}\;dx}\)

Since, \(\int \sqrt{a^{2}-x^{2}}\;dx = \frac{x}{2}\sqrt{a^{2}-x^{2}}+\frac{a^{2}}{2}\sin^{-1}\frac{x}{a}\)

\(\boldsymbol{\Rightarrow }\) \(\boldsymbol{\frac{3}{2}\;\left [ \frac{x}{2}\sqrt{2^{2}-(x)^{2}}+\frac{4}{2}\sin^{-1}\frac{x}{2} \right ]_{0}^{2}}\\\)

\(\boldsymbol{\Rightarrow }\) \(\boldsymbol{\frac{3}{2}[\frac{2}{2}\sqrt{4-4}+2\sin^{-1}(1)-0]=\frac{3\pi }{2}}\) unit²

Therefore, the Area enclosed by the curve ABOA \(\boldsymbol{=\frac{3\pi}{2}}\) unit²

Hence, the total Area enclosed by the ellipse ABA’B’ = 4 × \(\boldsymbol{\frac{3\pi}{2}}\) unit²

= 6π unit²

Q.10: Find the area enclosed by the curve x² + y² = 9, line x = \(2\sqrt{2}y\) and the first quadrant.

Sol:

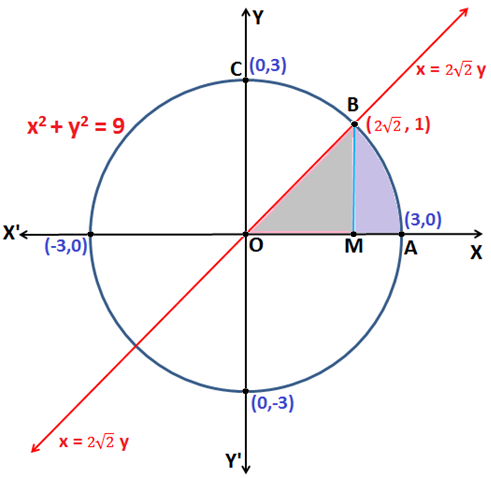
Equation x² + y² = 9 represents a circle with radius equal to 3units.

Since, x = \(2\sqrt{2}y\)

Therefore (\(2\sqrt{2}y\))² + y² = 9 (for points of intersection of both the curves)

Hence, the coordinates of point B = (\(2\sqrt{2}y\),1)

Now, the area of region bounded by the curve x² + y² = 9, x = \(2\sqrt{2}y\), and the first quadrant is the area enclosed by the curve OMABO.

i.e. Area of triangle OMB + Area under the curve MBAM.

Now, the Area of triangle = \(\frac{1}{2}\times Base \times Altitude\)

\(\boldsymbol{\Rightarrow }\) \(\frac{1}{2}\times OM \times BM\;=\;\frac{1}{2}\times2\sqrt{2}y\times 1 =\sqrt{2}\;y\;\)unit²

Now, the Area under the curve MBAM:

\(\boldsymbol{\Rightarrow }\) \(\int_{2\sqrt{2}}^{3}\;y\;dx\)

Since, x² +y² =9

Therefore, y² = 9 – x²

\(\boldsymbol{\Rightarrow }\) \(\boldsymbol{y=\sqrt{9-x^{2}}}\)

Since, \(\int \sqrt{a^{2}-x^{2}}\;dx = \frac{x}{2}\sqrt{a^{2}-x^{2}}+\frac{a^{2}}{2}\sin^{-1}\frac{x}{a}\\\)

\(\\\boldsymbol{\Rightarrow }\) \(\boldsymbol{\int_{2\sqrt{2}}^{3}\sqrt{3^{2}-x^{2}}\;dx=\left | \frac{x}{2}\sqrt{9-x^{2}}+\frac{9}{2}\;\sin^{-1}\frac{x}{3} \right |_{2\sqrt{2}}^{3}}\\\)

\(\\\boldsymbol{\Rightarrow }\) \(\;\boldsymbol{[\frac{3}{2}\times\ \sqrt{9-9}]+[\frac{9}{2}\;\sin^{-1}(1)]-[\frac{2\sqrt{2}}{2}\times \sqrt{9-8}]-[\frac{9}{2}\times \sin^{-1}\frac{2\sqrt{2}}{3}]}\\\)

\(\\\boldsymbol{\Rightarrow }\) \(\boldsymbol{\frac{9\pi }{4}-\sqrt{2}-[\frac{9}{2}\times \sin^{-1}\frac{2\sqrt{2}}{3}]}\\\) unit²

Therefore, the Area under the curve MBAM:

= \(\boldsymbol{\frac{9\pi }{4}-\sqrt{2}-[\frac{9}{2}\times \sin^{-1}\frac{2\sqrt{2}}{3}]}\)unit²

Now, total Area under the shaded region = Area under the curve MBAM + Area of the triangle OMB

\(\\\boldsymbol{\Rightarrow }\) \(\boldsymbol{\frac{9\pi }{4}-\sqrt{2}-[\frac{9}{2}\times \sin^{-1}\frac{2\sqrt{2}}{3}]+\sqrt{2}}\)

\(\\\boldsymbol{\Rightarrow }\) \(\boldsymbol{\frac{9\pi }{4}-[\frac{9}{2}\times \sin^{-1}\frac{2\sqrt{2}}{3}]}\) unit²

Hence, the required Area is given by the region OMABO:

\(\boldsymbol{=\frac{9\pi }{4}-[\frac{9}{2}\times \sin^{-1}\frac{2\sqrt{2}}{3}]}\)unit²

Q.11: Find the area of larger part of circle x² + y² = 16 cut off by the line x = \(\frac{4}{\sqrt{2}}\) in the first quadrant.

Sol:Based on formula given in Application of Integrals

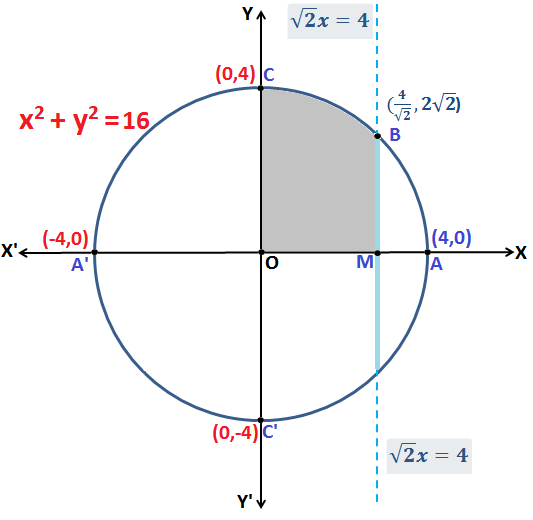
Equation x² + y² = 16 represents a circle with radius = 4 units.

For coordinates of point B:

\(\boldsymbol{\Rightarrow }\) \((\frac{4}{\sqrt{2}})^{2}+y^{2}=16\)

\(\boldsymbol{\Rightarrow }\) 8 + y² = 16

\(\boldsymbol{\Rightarrow }\) y = \(2\sqrt{2}\)

Hence, the coordinates of point B are: \(\boldsymbol{(\frac{4}{\sqrt{2}},2\sqrt{2})}\)

The required Area is given by the curve OMBCO:

\(\boldsymbol{\Rightarrow }\) \(\boldsymbol{\int_{0}^{2\sqrt{2}}y\;dx\;=\;\int_{0}^{2\sqrt{2}}\sqrt{16-x^{2}}\;dx}\)

Since, \(\\\int \sqrt{a^{2}-x^{2}}\;dx = \frac{x}{2}\sqrt{a^{2}-x^{2}}+\frac{a^{2}}{2}\sin^{-1}\frac{x}{a}\)

\(\\\boldsymbol{\Rightarrow }\) \(\boldsymbol{\left | \frac{x}{2}\sqrt{16-x^{2}}+\frac{16}{2}\sin^{-1} \frac{x}{4} \right |_{0}^{2\sqrt{2}}}\)

\(\\\boldsymbol{\Rightarrow }\) \(\boldsymbol{[\frac{2\sqrt{2}}{2}\sqrt{16-8}+8\sin^{-1}\frac{1}{\sqrt{2}}]-0}\)

\(\\\boldsymbol{\Rightarrow }\) \(\boldsymbol{\sqrt{2}\times 2\sqrt{2}+8\times \frac{\pi }{4}=[4+2\pi] }\) unit²

Therefore, the Area of shaded region OMBCO = [4 + 2π]unit²

 

 

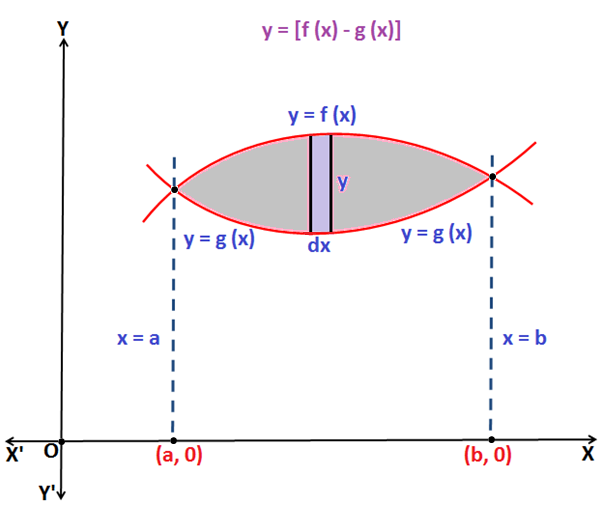
Let us assume two curves represented by the equation y = f(x) and y = g(x) in [a, b] as shown in the above figure. In this case the height of an elementary strip will be [f(x) – g(x)] and its width will be dx.

Now, Area of the elementary strip (dA) = [f(x) – g(x)] dx

Hence, the total Area of shaded region (A) = \(\int_{a}^{b} [f(x)-g(x)]\;dx\)

 

 

Example – 1: Find the area enclosed between two curves whose equations are: x² = 4y and y² = 4x.

Sol:Based on formula given in Application of Integrals

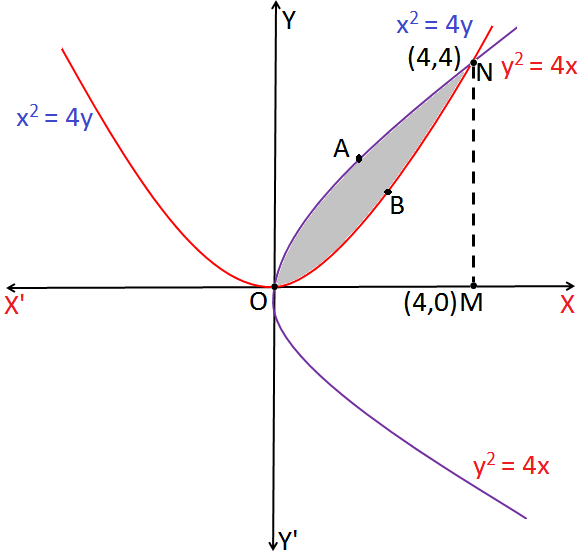
The Equation x² = 4y represents a parabola symmetrical about y-axis and the equation y² = 4x represents a parabola symmetrical about x-axis.

On solving both the equations:

\(\boldsymbol{\Rightarrow }\) \(\left ( \frac{y^{2}}{4} \right )^{2}=4y\)

\(\boldsymbol{\Rightarrow }\) y³ = 64 i.e. y = 4

Which gives x = 4. Hence, the coordinates of point N are (4, 4).

Now, The Area of region enclosed by the curve NAOBN = Area of region enclosed by the curve OANMO – Area of region enclosed by the curve OBNMO.

\(\boldsymbol{\Rightarrow }\) \(\boldsymbol{\int_{0}^{4}2\sqrt{x}\;dx-\int_{0}^{4}\frac{x^{2}}{4}\;dx}\)

\(\\\boldsymbol{\Rightarrow }\) \(\boldsymbol{\left [ 2\times \frac{2}{3}\times x^{\frac{3}{2}} \right ]_{0}^{4}-\left [ \frac{x^{3}}{12} \right ]_{0}^{4}}\)

\(\\\boldsymbol{\Rightarrow }\) \(\boldsymbol{\left [ \frac{4}{3}\times (4)^{\frac{3}{2}}-0 \right ]-\left [ \frac{64}{12}-0 \right ]= \frac{16}{3}}\) unit²

Therefore, the Area of shaded region = \(\frac{16}{3}\) unit²

 

 

EXAMPLE – 2: Find the area enclosed by the sides of a triangle whose vertices have coordinates (1, 0) (3, 5) and (5, 4).

Sol:Based on formula given in Application of Integrals

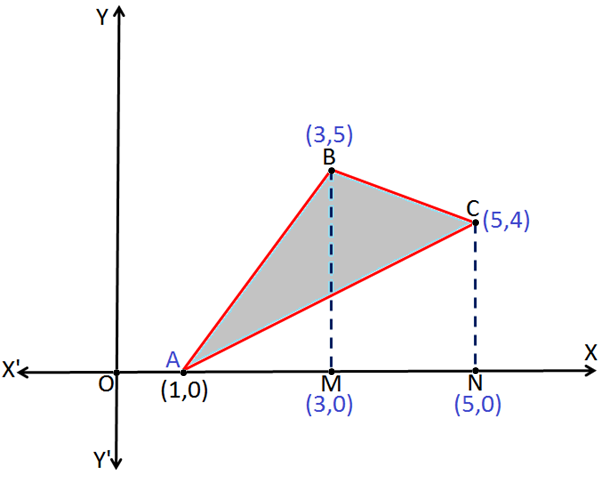
Form the above figure:

Let, A (1, 0), B (3, 5) and C (5, 4) be the vertices of triangle ABC.

Now, the equation of line AB:

Since, \((y-y_{1})=(x-x_{1})\times \left[\frac{y_{2}\;-\;y_{1}}{x_{2}\;-\;x_{1}}\right]\)

\(\boldsymbol{\Rightarrow }\) \((y-0)=(x-1)\times \left[\frac{5\;-\;0}{3\;-\;1}\right]\)

\(\boldsymbol{\Rightarrow }\) 2y = 5x – 5

\(\boldsymbol{\Rightarrow }\) \(\boldsymbol{y=\frac{5x\;-\;5}{2}}\)

The Equation of line BC:

Since, \((y-y_{1})=(x-x_{1})\times \left[\frac{y_{2}\;-\;y_{1}}{x_{2}\;-\;x_{1}}\right]\)

\(\boldsymbol{\Rightarrow }\) \((y-5)=(x-3)\times \left[\frac{4-5}{5-3}\right]\)

\(\boldsymbol{\Rightarrow }\) 2y – 10 = 3 – x

\(\boldsymbol{\Rightarrow }\) \(\boldsymbol{y=\frac{13\;-\;x}{2}}\)

The Equation of line AC:

Since, \((y-y_{1})=(x-x_{1})\times \left[\frac{y_{2}-y_{1}}{x_{2}-x_{1}}\right]\)

\(\boldsymbol{\Rightarrow }\) \((y-0)=(x-1)\times \left[\frac{4-0}{5-1}\right]\)

\(\boldsymbol{\Rightarrow }\) 4y = 4x – 4

\(\boldsymbol{\Rightarrow }\) y = x – 1

Now, the Area of triangle ABC = Area under the curve ABMA + Area under the curve MBCN – Area under the curve ACNA.

The Area under the curve ABMA [2y = 5x – 5]:

\(\\\boldsymbol{\Rightarrow }\) \(\boldsymbol{\int_{1}^{3}y\;dx\;=\;\int_{1}^{3}\frac{5x-5}{2}\;dx}\)

\(\\\boldsymbol{\Rightarrow }\) \(\boldsymbol{\left [ \frac{5x^{2}}{4}-\frac{5x}{2} \right ]_{1}^{3}}\)

\(\\\boldsymbol{\Rightarrow }\) \(\boldsymbol{\frac{45}{4}-\frac{15}{2}-\frac{5}{4}+\frac{5}{2}=5}\) unit²

Therefore, Area under the curve ABMA = 5 unit²

The Area under the curve MBCN [2y = 13 – x]:

\(\\\boldsymbol{\Rightarrow }\) \(\boldsymbol{\int_{3}^{5}y\;dx\;=\;\int_{3}^{5}\frac{13-x}{2}\;dx}\)

\(\\\boldsymbol{\Rightarrow }\) \(\boldsymbol{\left [ \frac{13x}{2}-\frac{x^{2}}{4} \right ]_{3}^{5}}\)

\(\\\boldsymbol{\Rightarrow }\) \(\boldsymbol{\frac{65}{2}-\frac{25}{4}-\frac{39}{2}+\frac{9}{4}=9}\) unit²

Therefore, Area under curve MBCN = 9 unit²

The Area under the curve ACNA [y = x – 1]:

\(\\\boldsymbol{\Rightarrow }\) \(\boldsymbol{\int_{1}^{5}y\;dx\;=\;\int_{1}^{5}(x-1)\;dx}\)

\(\\\boldsymbol{\Rightarrow }\) \(\boldsymbol{\left [ \frac{x^{2}}{2}-x \right ]_{1}^{5}}\)

\(\\\boldsymbol{\Rightarrow }\) \(\boldsymbol{\frac{25}{2}-5-\frac{1}{2}+1=8}\) unit²

Therefore, Area under the curve ACNA = 8 unit²

Now, Area of triangle ABC = Area under curve ABMA + Area under curve MBCN – Area under curve ACNA.

Therefore, the Area of triangle ABC = 5 + 9 – 8 = 6 unit²

Exercise – 8.2

Q.1: Find the area lying above the x-axis enclosed between two curves whose equations are given as: x² + y² = 6x and y² = 3x.

Sol:Based on formula given in Application of Integrals

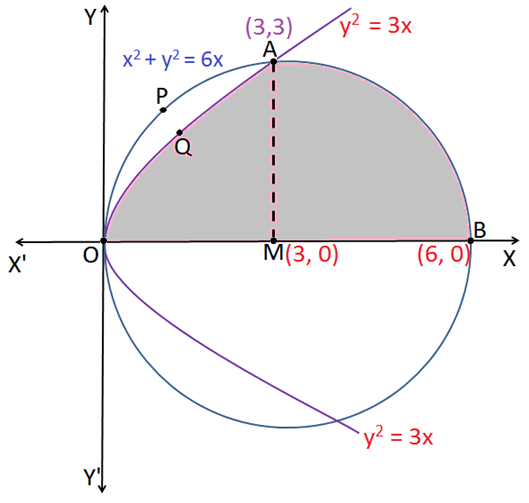
The Equation y² = 3x represents a parabola symmetrical about x-axis.

The Equation x² + y² = 6x i.e. (x – 3)² + y² = 9 represents a circle with centre (3, 0) and radius 3 units.

Substituting the equation of parabola in equation of circle:

(x – 3)² + 3x = 9 \(\boldsymbol{\Rightarrow}\) x² + 9 – 6x + 3x = 9

\(\boldsymbol{\Rightarrow}\) x² – 3x = 0 i.e. x = 0 or x = 3 which gives y = 0 and y = ± 3

Therefore, the coordinates of point A above the x-axis are (3, 3)

Now, the Area of region bounded by the curve OQABO = Area of region bounded by the curve OQAMO + Area of region bounded by the curve ABMA

The Area of region bounded by the curve OQAMO [y² = 3x]:

\(\\\boldsymbol{\Rightarrow}\) \(\boldsymbol{\int_{0}^{3}y\;dx=\int_{0}^{3}\sqrt{3x}\;dx}\)

\(\\\boldsymbol{\Rightarrow}\) \(\boldsymbol{\sqrt{3}\times\left [ \frac{2x^{\frac{3}{2}}}{3} \right ]_{0}^{3}=\sqrt{3}\times \frac{2}{3}\times 3^{\frac{3}{2}}}\\\)

\(\\\boldsymbol{\Rightarrow}\) \(\boldsymbol{\sqrt{3}\times \frac{2}{3}\times 3\sqrt{3}=6}\) unit²

Therefore, the Area of region bounded by the curve OQAMO = 6 unit²

Now, the Area of region bounded by the curve ABMA [(x – 3)² + y² = 9)]:

\(\boldsymbol{\Rightarrow}\) \(\boldsymbol{\int_{3}^{6}y\;dx=\int_{3}^{6}\sqrt{9-(x-3)^{2}}\;dx}\\\)

Since, \(\int \sqrt{a^{2}-(x-b)^{2}}\;dx = \frac{x-b}{2}\sqrt{a^{2}-(x-b)^{2}}+\frac{a^{2}}{2}\sin^{-1}\frac{x-b}{a}\\\)

\(\boldsymbol{\Rightarrow}\) \(\boldsymbol{\left [ \frac{x-3}{2}\sqrt{\left (3 \right )^{2}-\left ( x-3\right )^{2}}+\frac{9}{2}\sin^{-1}\frac{x-3}{3} \right ]_{3}^{6}}\\\)

\(\boldsymbol{\Rightarrow \;\;\;\left [\frac {6-3}{2}\sqrt{{9}-\left (6-3\right )^{2}}+\frac{9}{2}\sin^{-1}\frac{6-3}{3}\right]-\left [ \frac{x-3}{2}\;\sqrt{9-\left (3-3 \right )^{2}}\;+\frac{9}{2}\;\sin^{-1}\frac{3-3}{3}\;\right]}\\\)

\(\\\boldsymbol{\Rightarrow}\) \(\boldsymbol{\left [0 +\frac{9}{2}\times \sin^{-1}1-0\right ]=\frac{9}{2}\times \frac{\pi }{2}}\\\)

\(\\\boldsymbol{\Rightarrow}\) \(\boldsymbol{\frac{9\pi }{4}}\) unit²

Therefore, the Area of region bounded by the curve ABMA \(=\frac{9\pi }{4}\) unit²

The Area of region bounded by the curve OQABO = Area of region bounded by the curve OQAMO + Area of region bounded by the curve ABMA

\(\boldsymbol{\Rightarrow}\) \(6+\frac{9\pi }{4}=\frac{24+9\pi }{4}\) unit²

Therefore, the Area of shaded region (OQABO)\(=\frac{24+9\pi }{4}\) unit²

Q.2: Find the area enclosed between two curves: 9x² + 9y² = 4 and (x – \(\frac{2}{3}\))² + y² = \(\frac{4}{9}\)

Sol:Based on formula given in Application of Integrals

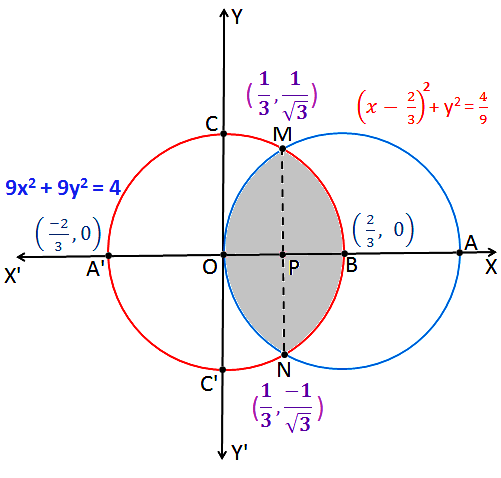
Equation 9x² + 9y² = 4 . . . . . . . (1), represents a circle with centre (0, 0) and radius 3 units.

Equation (x – \(\frac{2}{3}\) )² + y² = \(\frac{4}{9}\) . . . . . . . . . . .(2), represents a circle with centre (3, 0) and radius 3 units.

On solving equation (1) and equation (2), we will get:

\(\\\boldsymbol{\Rightarrow }\) \((x-\frac{2}{3})^{2}+\frac{4-9x^{2}}{9}=\frac{4}{9}\)

\(\\\boldsymbol{\Rightarrow }\) \(x^{2}+\frac{4}{9}-\frac{4x}{3}+\frac{4}{9}-x^{2}=\frac{4}{9}\)

\(\\\boldsymbol{\Rightarrow }\) \(\frac{4}{9}=\frac{4}{3}\;x\)

\(\\\boldsymbol{\Rightarrow }\) \(\boldsymbol{x=\frac{1}{3}}\) which gives \(\boldsymbol{y=\pm \frac{1}{\sqrt{3}}}\)

Therefore, the coordinates of points M and N are: \((x=\frac{1}{3})\;\;(y=\pm \frac{1}{\sqrt{3}})\)

Now, the Area enclosed by region BMONB = 2 × [Area enclosed by the curve BMOB].

And the Area enclosed by the curve BMOB = Area of region enclosed by the curve (MOPM+MPBM).

Now, the Area of region enclosed by the curve MPBM [9x² + 9y² = 4]:

\(\\\boldsymbol{\Rightarrow }\) \(\boldsymbol{\int_{\frac{1}{3}}^{\frac{2}{3}}y\;dx=\int_{\frac{1}{3}}^{\frac{2}{3}}\sqrt{\frac{4}{9}-x^{2}}\;dx}\)

Since, \(\\\int \sqrt{a^{2}-x^{2}}\;dx = \frac{x}{2}\sqrt{a^{2}-x^{2}}+\frac{a^{2}}{2}\sin^{-1}\frac{x}{a}\)

\(\\\boldsymbol{\Rightarrow }\) \(\boldsymbol{\left [ \frac{x}{2}\sqrt{\left ( \frac{2}{3} \right )^{2}-x^{2}}+\frac{4}{2\times 9}\sin^{-1}\frac{3x}{2} \right ]_{\frac{1}{3}}^{\frac{2}{3}}}\\\)

\(\\\boldsymbol{\Rightarrow }\) \(\boldsymbol{\left [\frac{1}{3}\times \sqrt{\frac{4}{9}-\frac{4}{9}}+\frac{2}{9}\sin^{-1}(1) \right ] -\left [ \frac{1}{6}\times \sqrt{\frac{4}{9}-\frac{1}{9}}+\frac{2}{9}\sin^{-1}\frac{1}{2}\right ] }\\\)

\(\\\boldsymbol{\Rightarrow }\) \(\boldsymbol{\left [ 0+\frac{2}{9}\times \frac{\pi }{2} \right ]-\left [ \frac{1}{6}\times \frac{1}{\sqrt{3}}+\frac{2}{9}\times \frac{\pi }{6} \right ]=\left [\frac{2\pi }{27}-\frac{ 1}{6\sqrt{3}} \right ]}\) unit²

Therefore, area of region enclosed by the curve MPBM \(=\left [\frac{2\pi }{27}-\frac{ 1}{6\sqrt{3}} \right ]\) unit²

Now, the Area of region enclosed by the curve MOPM \(\left [ \left ( x-\frac{2}{3} \right )^{2}+y^{2}=\frac{4}{9} \right ]\) :

\(\\\boldsymbol{\Rightarrow }\) \(\boldsymbol{\int_{0}^{\frac{1}{3}}y\;dx=\int_{0}^{\frac{1}{3}}\sqrt{\left ( \frac{2}{3} \right )^{2}-\left ( x-\frac{2}{3} \right )^{2}}\;dx}\\\)

Since, \(\\\int \sqrt{a^{2}-(x-b)^{2}}\;dx = \frac{x-b}{2}\sqrt{a^{2}-(x-b)^{2}}+\frac{a^{2}}{2}\sin^{-1}\frac{x-b}{a}\)

\(\boldsymbol{\Rightarrow }\) \(\boldsymbol{\left [ \frac{x-\frac{2}{3}}{2}\sqrt{\left ( \frac{2}{3} \right )^{2}-\left ( x-\frac{2}{3} \right )^{2}}+\frac{2}{9}\sin^{-1}\frac{x-\frac{2}{3}}{\frac{2}{3}} \right ]_{0}^{\frac{1}{3}}}\\\)

\(\\\boldsymbol{\Rightarrow }\) \(\boldsymbol{\left [ \frac{\frac{1}{3}-\frac{2}{3}}{2}\sqrt{\frac{4}{9}-\left ( \frac{1}{3}-\frac{2}{3} \right )^{2}}+\frac{2}{9}\sin^{-1}\frac{\frac{1}{3}-\frac{2}{3}}{\frac{2}{3}} \right]- \left [ \frac{0-\frac{2}{3}}{2}\;\sqrt{\frac{4}{9}-\left ( 0-\frac{2}{3} \right )^{2}}\;+\frac{2}{9}\;\sin^{-1}\frac{0-\frac{2}{3}}{\frac{2}{3}}\; \right ]}\\\)

\(\boldsymbol{\Rightarrow }\) \(\boldsymbol{\left [ \frac{-1}{6}\times \sqrt{\frac{4}{9}-\frac{1}{9}}+\frac{2}{9}\times \sin^{-1}\frac{-1}{2} \right ]- \left [ \frac{-1}{3}\times \sqrt{\frac{4}{9}-\frac{4}{9}}+\frac{2}{9}\times \sin^{-1}(-1) \right ]}\\\)

\(\boldsymbol{\Rightarrow }\) \(\boldsymbol{\left [ \frac{-1}{6\sqrt{3}}+\frac{2}{9}\times \frac{-\pi }{6} \right ]-\left [ \frac{2}{9}\times \frac{-\pi }{2} \right ]= \left [ \frac{2\pi }{27}-\frac{1}{6\sqrt{3}} \right ]}\) unit²

Therefore, the Area of region enclosed by the curve MOPM \(= \left [ \frac{2\pi }{27}-\frac{1}{6\sqrt{3}} \right ]\) unit²

Now, the Area enclosed by the curve BMOB = Area of region enclosed by the curve (MOPM+MPBM)

\(\boldsymbol{\Rightarrow }\) \(\left [ \frac{2\pi }{27}-\frac{1}{6\sqrt{3}} \right ] +\left [\frac{2\pi }{27}-\frac{ 1}{6\sqrt{3}} \right ]\\\)

\(\boldsymbol{\Rightarrow }\) \(\boldsymbol{\left [ \frac{4\pi }{27}-\frac{1}{3\sqrt{3}} \right ]}\) unit²

Now, the Area enclosed by the curve BMONB = 2 [Area enclosed by the curve BMOB] \(=2\times \left [ \frac{4\pi }{27}-\frac{1}{3\sqrt{3}} \right ]\) unit²

Therefore, the Area of shaded region = \(\left [ \frac{8\pi }{27}-\frac{2}{3\sqrt{3}} \right ]\) unit²

Q.3: Find the area lying above the x-axis enclosed between two curves whose equations are given as: 4x² + 4y² = 9 and x² = 4y.

Sol:Based on formula given in Application of Integrals

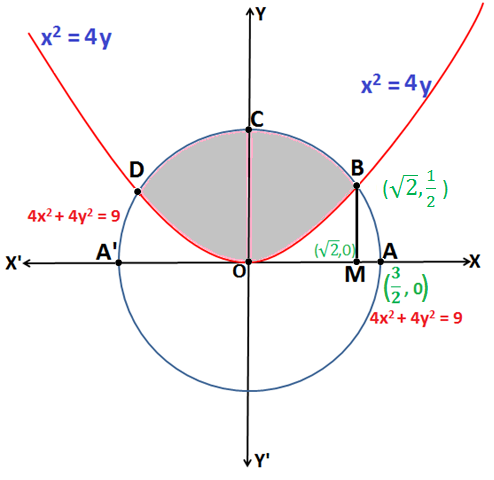
The Equation x² = 4y represents a parabola symmetrical about y-axis.

The Equation 4x² + 4y² = 9 i.e. x² + y² = \(\frac{3}{2}\) represents a circle with centre (0, 0) and radius \(\frac{3}{2}\) units.

Now, on substituting the equation of parabola in the equation of circle we will get:

4(4y) + 4y² =9 i.e. 4y² + 16y – 9 = 0

From the above quadratic equation: a = 4, b = 16 and c = -9

Substituting the values of a, b and c in quadratic formula:

\(\\\boldsymbol{\Rightarrow }\) \(\\y=\frac{-16+\sqrt{(16)^{2}-4(4\times-9)}}{2\times 4}\;and\;y=\frac{-16-\sqrt{(16)^{2}-4(4\times -9)}}{2\times 4}\)

\(\\\boldsymbol{\Rightarrow }\) \(\\ y=\frac{-16+\sqrt{256+144}}{8}\;and\;y=\frac{-16-\sqrt{256+144}}{8}\)

\(\\\boldsymbol{\Rightarrow }\) \(\\ y=\frac{-16+\sqrt{400}}{8}\;and\;y= \frac{-16-\sqrt{400}}{8}\)

\(\\\boldsymbol{\Rightarrow }\) \(\\ y=\frac{-16+20}{8}\;and\;y=\frac{-16-20}{8}\)

\(\\\boldsymbol{\Rightarrow }\) \(y = \frac{1}{2}\;\;and\;\;y = \frac{-9}{2}\)

Which gives x = \(\pm \;\sqrt{2}\) [Neglecting y = \(\frac{-9}{2}\) as it gives absurd results]

Therefore, the coordinates of point B are \(\left (\sqrt{2},\;\frac{1}{2} \right )\)

Now, Area of region bounded by the curve ODCBO = 2 × (Area of region bounded by the curve OBCO)

Now, Area of region bounded by curve OBCO = (Area of region bounded by the curve OCBMO + Area of region bounded by the curve OBMO)

Area of region bounded by the curve OCBMO [4x ² + 4y² = 9]:

\(\\\boldsymbol{\Rightarrow }\) \(\boldsymbol{\int_{0}^{\sqrt{2}}y\;dx=\int_{0}^{\sqrt{2}}\sqrt{\left ( \frac{3}{2} \right )^{2}-x^{2}}\;\;dx}\)

Since, \(\\\int \sqrt{a^{2}-b^{2}}\;dx = \frac{x}{2}\sqrt{a^{2}-x^{2}}+\frac{a^{2}}{2}\sin^{-1}\frac{x}{a}\)

\(\\\boldsymbol{\Rightarrow }\) \(\boldsymbol{\left [ \frac{x}{2}\sqrt{\frac{9}{4}- x^{2}}+\frac{9}{2\times 4}\sin^{-1}\frac{2\times x}{3} \right ]_{0}^{\sqrt{2}}}\\\)

\(\\\boldsymbol{\Rightarrow }\) \(\boldsymbol{\left [\frac {\sqrt{2}}{4}\times \sqrt{{\frac{9}{4}-2}}+\frac{9}{8}\sin^{-1}\frac{2\sqrt{2}}{3}\right]-0}\\\)

\(\\\boldsymbol{\Rightarrow }\) \(\boldsymbol{\left [\sqrt{2}\times \frac{1}{4}+\frac{9}{8}\sin^{-1}\frac{2\sqrt{2}}{3}\right ]\\}\) unit²

Therefore, Area of region bounded by the curve ABMA = \(\left [\sqrt{2}\times \frac{1}{4}+\frac{9}{8}\sin^{-1}\frac{2\sqrt{2}}{3}\right]\) unit²

Area of region bounded by the curve OBMO [x² = 4y]:

\(\\\boldsymbol{\Rightarrow }\) \(\boldsymbol{\int_{0}^{\sqrt{2}}y\;dx=\int_{0}^{\sqrt{2}}\frac{x^{2}}{4}\;dx}\)

\(\\\boldsymbol{\Rightarrow }\) \(\boldsymbol{\left [ \frac{x^3}{12} \right ]_{0}^{\sqrt{2}}=\frac{2\sqrt{2}}{12}-0}\\\)

\(\\\boldsymbol{\Rightarrow }\) \(\boldsymbol{\frac{1}{3\sqrt{2}}}\) unit²

Therefore, the area of region bounded by the curve OBMO = \(\frac{1}{3\sqrt{2}}\) unit²

Now, the Area of region bounded by curve OBCO = [Area of region bounded by the curve OCBMO – Area of region bounded by the curve OBMO]

\(\\\boldsymbol{\Rightarrow }\) \(\left [\sqrt{2}\times \frac{1}{4}+\frac{9}{8}\sin^{-1}\frac{2\sqrt{2}}{3}\right]-\frac{1}{3\sqrt{2}}\)

\(\\\boldsymbol{\Rightarrow }\) \(\left [ \frac{\sqrt{2}}{12}+\frac{9}{8}\sin^{-1}\frac{2\sqrt{2}}{3} \right ]\) unit²

Therefore, Area of region bounded by the curve OBCO = \(\left [ \frac{\sqrt{2}}{12}+\frac{9}{8}\sin^{-1}\frac{2\sqrt{2}}{3} \right ]\) unit²

Now, the Area of region bounded by the curve ODCBO = 2 × [Area of region bounded by the curve OBCO]

\(\\\boldsymbol{\Rightarrow }\) \(2\times \left [\frac{\sqrt{2}}{12}+\frac{9}{8}\sin^{-1}\frac{2\sqrt{2}}{3} \right ]\)

Therefore, the Area of shaded region = \(\left [ \frac{1}{2\sqrt{2}}+\frac{9}{4}\sin^{-1}\frac{2\sqrt{2}}{3} \right ]\) unit²

Q.4: Find the area enclosed by the sides of a triangle whose vertices have coordinates (-2, 0) (3, 4) and (5, 2).

Sol:Based on formula given in Application of Integrals

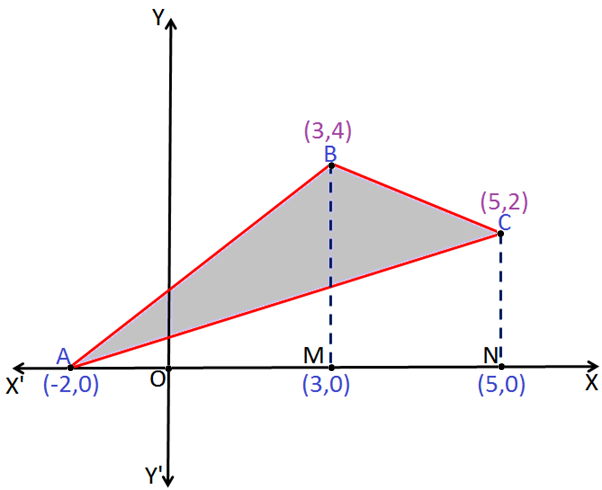
Form the above figure:

Let, A (1, 0), B (3, 5) and C (5, 4) be the vertices of triangle ABC

Now, the equation of line AB:

Since, \((y-y_{1})=(x-x_{1})\times \left[\frac{y_{2}\;-\;y_{1}}{x_{2}\;-\;x_{1}}\right]\)

\(\\\boldsymbol{\Rightarrow }\) \((y-0)\;=\;(x+2)\times \left[\frac{4\;-\;0}{3\;+\;2}\right]\)

\(\\\boldsymbol{\Rightarrow }\) 5y = 4x + 8

\(\\\boldsymbol{\Rightarrow }\) \(\boldsymbol{y=\frac{4x\;+\;8}{5}}\)

The Equation of line BC:

Since, \((y-y_{1})=(x-x_{1})\times \left[\frac{y_{2}\;-\;y_{1}}{x_{2}\;-\;x_{1}}\right]\)

\(\\\boldsymbol{\Rightarrow }\) \((y-4)=(x-3)\times \left[\frac{2\;-\;4}{5\;-\;3}\right]\)

\(\\\boldsymbol{\Rightarrow }\) 2y – 8 = 6 – 2x

\(\\\boldsymbol{\Rightarrow }\) y = 7 – x

The Equation of line AC:

Since, \((y-y_{1})=(x-x_{1})\times \left[\frac{y_{2}\;-\;y_{1}}{x_{2}\;-\;x_{1}}\right]\)

\(\\\boldsymbol{\Rightarrow }\) \((y-0)=(x+2)\times \left[\frac{2\;-\;0}{5\;+\;2}\right]\)

\(\\\boldsymbol{\Rightarrow }\) 7y = 2x + 4

\(\\\boldsymbol{\Rightarrow }\) \(\boldsymbol{ y= \frac{2\;x+4}{7}}\)

Now, the Area of triangle ABC = Area under the curve ABMA + Area under the curve MBCN – Area under the curve ACNA.

The Area under the curve ABMA:

\(\\\boldsymbol{\Rightarrow }\) \(\boldsymbol{\int_{-2}^{3}y\;dx\;=\;\int_{-2}^{3}\frac{4x\;+\;8}{5}\;dx}\\\) = \(\boldsymbol{\left [ \frac{4x^{2}}{10}+\frac{8x}{5} \right ]_{-2}^{3}}\\\)

\(\\\boldsymbol{\Rightarrow }\) \(\boldsymbol{\frac{36}{10}+\frac{24}{5}-\frac{16}{10}-\frac{-16}{5}=10}\) unit²

Therefore, the Area under the curve ABMA = 10 unit²

The Area under the curve MBCN:

\(\\\boldsymbol{\Rightarrow }\) \(\boldsymbol{\int_{3}^{5}y\;dx\;=\;\int_{3}^{5}=(7-x)\;dx}\\\) = \(\boldsymbol{\left [ 7x-\frac{x^{2}}{2} \right ]_{3}^{5}}\\\)

\(\\\boldsymbol{\Rightarrow }\) \(\boldsymbol{35-\frac{25}{2}- 21+\frac{9}{2}=6}\) unit²

Therefore, the Area under the curve MBCN = 6 unit²

The Area under the curve ACNA:

\(\\\boldsymbol{\Rightarrow }\) \(\boldsymbol{\int_{-2}^{5}y\;dx\;=\;\int_{-2}^{5}\frac{2x\;+\;4}{7}\;dx}\\\) = \(\boldsymbol{\left [ \frac{2x^{2}}{14}+\frac{4x}{7}\right ]_{-2}^{5}}\\\)

\(\\\boldsymbol{\Rightarrow }\) \(\boldsymbol{\frac{25}{7}+\frac{20}{7}-\frac{4}{7}-\frac{-8}{7}=7}\) unit²

Therefore, the Area under the curve ACNA = 7 unit²

Now, Area of triangle ABC = Area under curve ABMA + Area under curve MBCN – Area under curve ACNA.

Therefore, the Area of triangle ABC = 10 + 6 – 7 = 9 unit²

Q.5: Find the area enclosed by the sides of a triangle whose equations are: y = 4x + 2, y = 3x + 2 and x = 5.

Sol:Based on formula given in Application of Integrals

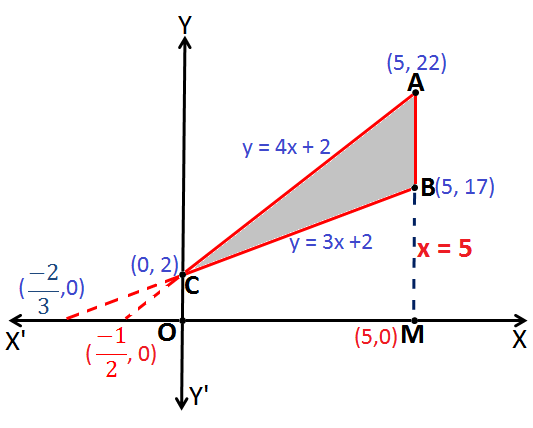
From the above figure,

The Equation of side AC: y = 4x + 2 . . . . . . (1)

The Equation of side BC: y =3x + 2 . . . . . . (2)

And, x = 5 . . . . . . . . . . (3)

From equation (1) and equation (3):

y = 4(5) + 2 = 22 [Since, x = 5]

Therefore, the coordinates of point A are (5, 22).

From equation (2) and equation (3):

y = 3(5) + 2 = 17 [Since, x = 5]

Therefore, the coordinates of point B are (5, 17).

Now, substituting equation (1) in equation (2):

3x + 2 = 4x + 2 i.e. x = 0 and y = 2

Therefore, the coordinates of point C are (0, 2).

Now, the Area of triangle ABC = Area enclosed by the curve ACOMA – Area enclosed by the curve COMBC.

The Area under the curve ACOMA [y = 4x + 2]:

\(\\\boldsymbol{\Rightarrow }\) \(\boldsymbol{\int_{0}^{5}y\;dx\;=\;\int_{0}^{5}(4x+2)\;dx}\)

\(\\\boldsymbol{\Rightarrow }\) \(\boldsymbol{\left [ \frac{4x^{2}}{2}+2x \right ]_{0}^{5}}\)

\(\\\boldsymbol{\Rightarrow }\) \(\boldsymbol{50+10-0=60}\) unit²

Therefore, the Area under the curve ABMA = 60 unit².

The Area under the curve MBCN [y = 3x + 2]:

\(\\\boldsymbol{\Rightarrow }\) \(\boldsymbol{\int_{0}^{5}y\;dx\;=\;\int_{0}^{5}(3x+2)\;dx}\)

\(\\\boldsymbol{\Rightarrow }\) \(\boldsymbol{\left [ \frac{3x^{2}}{2}+2x \right ]_{0}^{5}}\)

\(\\\boldsymbol{\Rightarrow }\) \(\boldsymbol{\frac{75}{2}+10-0=47.5}\) unit²

Therefore, the Area under the curve MBCN = 47.5 unit².

Now, the Area of triangle ABC = Area enclosed by the curve ACOMA – Area enclosed by the curve COMBC

\(\\\boldsymbol{\Rightarrow }\) 60 – 47.5 = 12.5 unit²

Therefore, the Area of triangle ABC = 12.5 unit²

Q.6: Find the area enclosed by the curves y = x² + 3, y = 2x, x = 2 and x =0.

Sol:Based on formula given in Application of Integrals

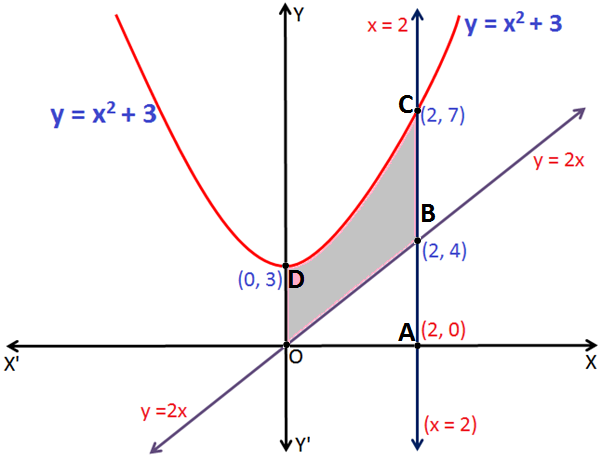
The Equation y = x² + 3 represents a parabola symmetrical about y-axis.

On substituting equation of line x = 2 in the equation of parabola we will get the coordinates of point C i.e. (2, 7).

On substituting x = 2 in the equation of line y = 2x we will get the coordinates of point B i.e. (2, 4).

From the above figure,

The Area of region enclosed by the curve ODCBO = Area of region enclosed by the curve ODCAO – Area of region enclosed by the curve OBAO

Now, the Area of region enclosed by the curve ODCAO [y = x² + 3]:

\(\\\boldsymbol{\Rightarrow }\) \(\boldsymbol{\int_{0}^{2}y\;dx = \int_{0}^{2}(x^{2}+3)\;dx}\)

\(\\\boldsymbol{\Rightarrow }\) \(\boldsymbol{\left [ \frac{x^{3}}{3}+3x \right ]_{0}^{2}=\frac{8}{3}+6=\frac{26}{3}}\)unit²

Therefore, the Area of region enclosed by the curve ODCAO = \(\frac{26}{3}\) unit²

Now, the Area of region enclosed by the curve OBAO [y = 2x]:

\(\\\boldsymbol{\Rightarrow }\) \(\boldsymbol{\int_{0}^{2}y\;dx = \int_{0}^{2}(2x)\;dx}\)

\(\\\boldsymbol{\Rightarrow }\) \(\boldsymbol{\left [x^{2} \right ]_{0}^{2}=4}\) unit²

Therefore, the Area of region enclosed by the curve OBAO = 4 unit²

Now, the Area of region enclosed by the curve ODCBO = Area of region enclosed by the curve ODCAO – Area of region enclosed by the curve OBAO

\(\Rightarrow \frac{26}{3}-4=\frac{2}{3}\) unit²

Therefore, The Area of shaded region (ODCBO) = \(\frac{2}{3}\)unit²

Q.7: Find the area enclosed between the curve y² = 6x and line y = 3x.

Sol:Based on formula given in Application of Integrals

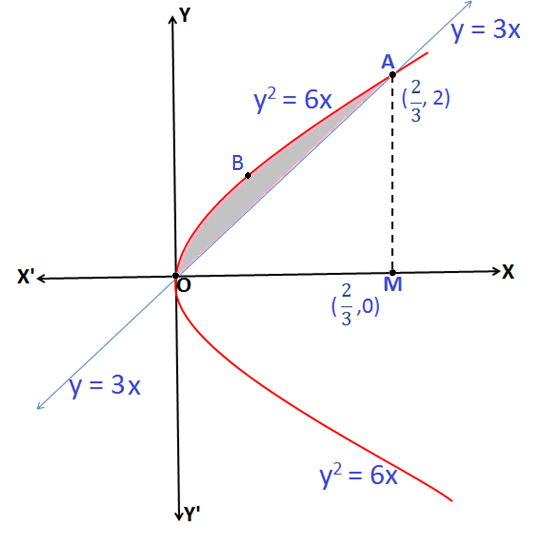
Equation y² = 6x represents a parabola, symmetrical about x-axis.

Now, substituting the Equation of line y = 3x in the equation of parabola:

(3x)² = 6x \(\Rightarrow x = \frac{2}{3}\) which gives y = 2

Hence the coordinates of point A are \((\frac{2}{3},2)\)

The area of region enclosed by the curve OABO = Area enclosed by the curve OMABO – Area enclosed by the curve OAMO

Now, the Area enclosed by the curve OMABO [y² = 6x]:

Since, y² = 6x

Therefore, y = \(\sqrt{6x}\)

\(\\\boldsymbol{\Rightarrow }\) \(\boldsymbol{\int_{0}^{\frac{2}{3}} y\;dx = \int_{0}^{\frac{2}{3}}\sqrt{6x}\;dx}\)

\(\boldsymbol{\Rightarrow }\) \(\boldsymbol{\sqrt{6}\left [ \frac{2}{3}\times x^{\frac{3}{2}} \right ]_{0}^{\frac{2}{3}}=\sqrt{6}\times \frac{2}{3}\times \left ( \frac{2}{3} \right )^{\frac{3}{2}}}\\\)

\(\\\boldsymbol{\Rightarrow }\) \(\boldsymbol{\sqrt{2} \times \sqrt{3}\times \frac{2}{3}\times 2\sqrt{2}\times \frac{1}{3\sqrt{3}}=\frac{8}{9}}\\\) unit²

Therefore, the Area enclosed by the curve OMABO = \(\frac{8}{9}\) unit²

Now, the Area enclosed by the curve OAMO [y = 3x]:

\(\\\boldsymbol{\Rightarrow }\) \(\boldsymbol{\int_{0}^{\frac{2}{3}} y\;dx\Rightarrow \int_{0}^{\frac{2}{3}}3x\;dx}\)

\(\boldsymbol{\Rightarrow }\) \(\boldsymbol{3\left [\frac{x^{2}}{2}\right ]_{0}^{\frac{2}{3}}=\frac{3}{2}\times \left ( \frac{2}{3} \right )^2}\) = \(\boldsymbol{\frac{2}{3}}\) unit²

Therefore, the Area enclosed by the curve OAMO = \(\frac{2}{3}\) unit²

Now, the area of region enclosed by the curve OABO = Area enclosed by the curve OMABO – Area enclosed by the curve OAMO

\(\\\boldsymbol{\Rightarrow }\) \(\frac{8}{9}-\frac{2}{3} = \frac{2}{9}\) unit²

Therefore, the Area enclosed by the curve OABO = \(\frac{2}{9}\) unit²

Miscellaneous Exercise

 

Q.1: Find the area enclosed by the curve whose equations are: y = 2x², x = 2, x = 3 and x-axis.

Sol:

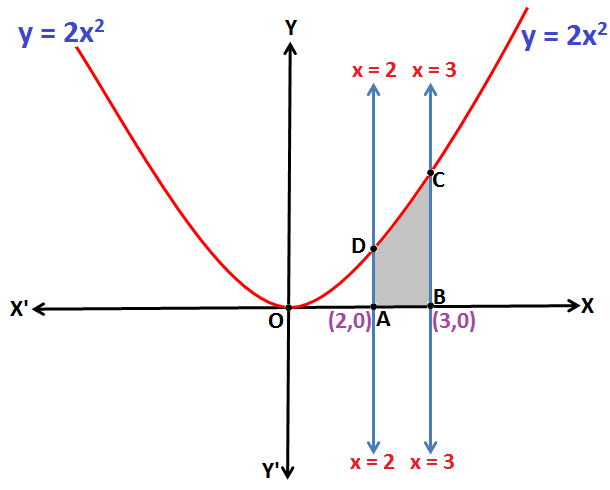
The equation y = 2x² represents a parabola symmetrical about y-axis.

Now, the Area of region enclosed by the curve ABCDA [y = 2x²]:

\(\\\boldsymbol{\Rightarrow }\) \(\boldsymbol{\int_{2}^{3}y\;dx=\int_{2}^{3}2x^{2}\;dx}\)

\(\\\boldsymbol{\Rightarrow }\) \(\boldsymbol{\left [ \frac{2x^{3}}{3} \right ]_{2}^{3}=\left [ 18-\frac{16}{3} \right ]=\frac{38}{3}}\) unit²

Therefore, the Area of shaded region \(=\frac{38}{3}\) unit²

Q.2: Find the area enclosed by the curve whose equations are: y = 5x⁴, x = 3, x = 7 and x-axis.

Sol:Based on formula given in Application of Integrals

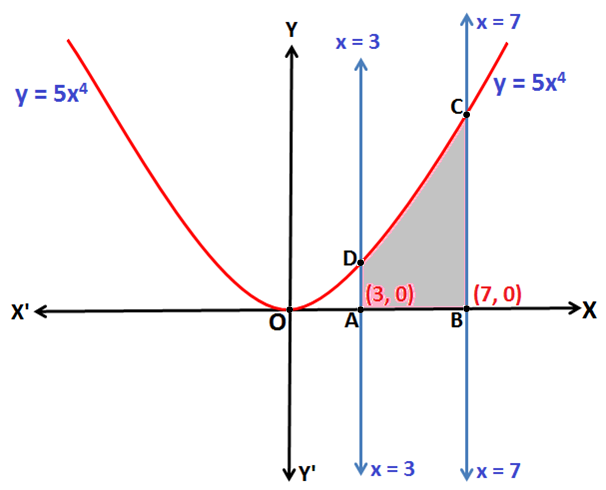
The equation y = 2x² represents a quartic parabola symmetrical about y-axis.

Now, the Area of region enclosed by the curve ABCDA [y = 5x⁴]:

\(\\\boldsymbol{\Rightarrow }\) \(\boldsymbol{\int_{3}^{7}y\;dx=\int_{3}^{7}5x^{4}\;dx}\)

\(\\\boldsymbol{\Rightarrow }\) \(\boldsymbol{\left [ \frac{5x^{5}}{5} \right ]_{3}^{7}=\left [ 16807-243 \right ]=16564}\) unit²

Therefore, the Area of shaded region = 16807 unit²

Q.3: Find the area enclosed between the curve y² = 3x and line y = 6x.

Sol:Based on formula given in Application of Integrals

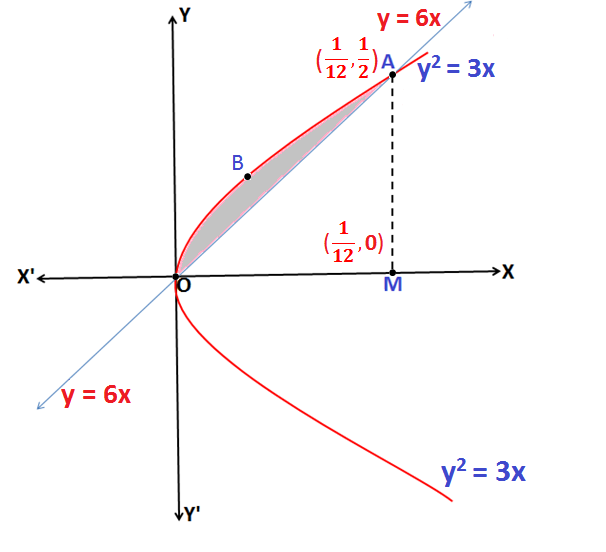
Equation y² = 3x represents a parabola, symmetrical about x-axis.

Now, substituting the Equation of line y = 6x in the equation of parabola:

(6x)² = 3x \(\Rightarrow x = \frac{1}{12}\) which gives y = \(\frac{1}{2}\)

Hence the coordinates of point A are \((\frac{1}{12},\frac{1}{2})\)

The Area of region enclosed by the curve OABO = Area enclosed by the curve OMABO – Area enclosed by the curve OAMO

Now, the Area enclosed by the curve, OMABO [y² = 3x]:

Since, y² = 3x

Therefore, y = \(\sqrt{3x}\)

\(\\\boldsymbol{\Rightarrow }\) \(\boldsymbol{\int_{0}^{\frac{1}{12}} y\;dx = \int_{0}^{\frac{1}{12}}\sqrt{3x}\;dx}\)

\(\\\boldsymbol{\Rightarrow }\) \(\boldsymbol{\sqrt{3}\left [ \frac{2}{3}\times x^{\frac{3}{2}} \right ]_{0}^{\frac{1}{12}}=\sqrt{3}\times \frac{2}{3}\times \left ( \frac{1}{12} \right )^{\frac{3}{2}}}\)

\(\\\boldsymbol{\Rightarrow }\) \(\boldsymbol{\sqrt{3} \times \frac{2}{3}\times \frac{1}{24\sqrt{3}}=\frac{1}{36}}\) unit²

Therefore, the Area enclosed by the curve OMABO = \(\frac{1}{36}\)unit²

Now, the Area enclosed by the curve OAMO [y = 6x]:

\(\\\boldsymbol{\Rightarrow }\) \(Area\;of \;\Delta OAM = \frac{1}{2}\times Base\times Altitude\)

\(\\\boldsymbol{\Rightarrow }\) \(\frac{1}{2}\times |OM|\times |AM|=\boldsymbol{\frac{1}{2}\times \frac{1}{12}\times \frac{1}{2}}\)

\(\\\boldsymbol{\Rightarrow }\) \(\boldsymbol{\frac{1}{48}}\)unit²

Therefore, the Area enclosed by the curve OAMO = \(\frac{1}{48}\)unit²

Now, the area of region enclosed by the curve OABO = Area enclosed by the curve OMABO – Area enclosed by the curve OAMO

\(\\\boldsymbol{\Rightarrow }\) \(\frac{1}{36}-\frac{1}{48} = \frac{1}{144}\)unit²

Therefore, the Area enclosed by the curve OABO = \(\frac{1}{144}\)unit²

Q.4 Find the area enclosed by the curve y = 2x² and the lines y = 1, y = 3 and the y-axis.

Sol:Based on formula given in Application of Integrals

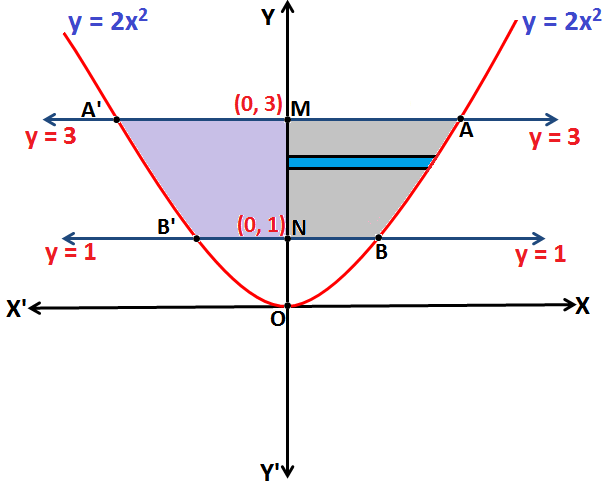
Equation y = 2x² represents a parabola symmetrical about y-axis.

The Area of the region bounded by the curve y = 2x², y = 1, and y = 3, is the Area enclosed by the curve AA’B’BA.

Now, the Area of region AA’B’BA = 2 (Area of region ABNMA)

Since, 2x² = y

Therefore, x = \(\sqrt{\frac{y}{2}}\)

Thus, the Area of region bounded by the curve ABNMA [y = 2x²]:

\(\\\boldsymbol{\Rightarrow }\) \(\boldsymbol{\int_{1}^{3}x\;dy=\int_{1}^{3}\sqrt{\frac{y}{2}}\;dx}\)

\(\\\boldsymbol{\Rightarrow }\) \(\boldsymbol{\frac{1}{\sqrt{2}}\times {\left | \frac{2}{3}\times (y)^{\frac{3}{2}} \right |_{1}^{3}=\frac{\sqrt{2}}{3}\times [(3^{\frac{3}{2}})-(1)^{\frac{3}{2}}}}]\\\)

\(\\\boldsymbol{\Rightarrow }\) \(\boldsymbol{\frac{\sqrt{2}}{3}\times (3\sqrt{3}-1) = \frac{\sqrt{2}}{3}(3\sqrt{3}-1)}\)unit²

Therefore, the Area of region bounded by the curve ABNMA = \(\frac{\sqrt{2}}{3}(3\sqrt{3}-1)\)unit²

Hence, the Area of region bounded by the curve AA’B’BA = 2(Area of region bounded by the curve ABNMA)\(= \frac{2\sqrt{2}}{3}(3\sqrt{3}-1)\)unit²

 

 

Q.5: Find the area enclosed between the curve y² = 9ax and line y = mx.

Sol:Based on formula given in Application of Integrals

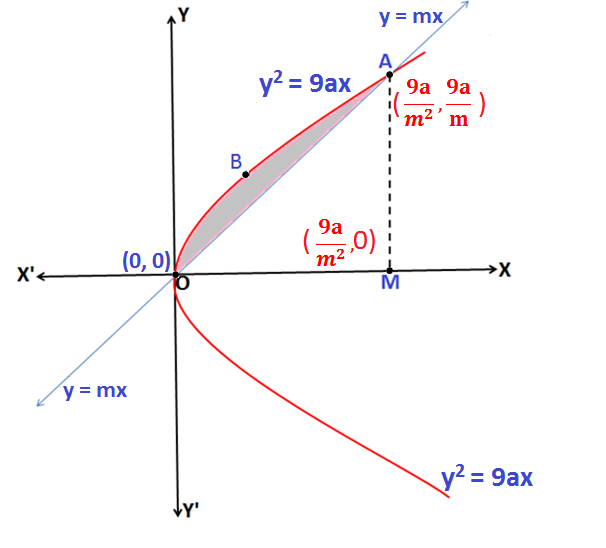
Equation y² = 9ax represents a parabola, symmetrical about x-axis.

Now, substituting the Equation of line y = mx in the equation of parabola:

9ax = (mx)² i.e x = \(\frac{9a}{m^{2}}\) which gives y = \(\frac{9a}{m}\)

Hence the co-ordinates of point A are \(\left ( \frac{9a}{m^{2}},\frac{9a}{m}\right )\)

The Area of region enclosed by the curve OABO = Area enclosed by the curve OMABO – Area enclosed by the curve OAMO

Now, the Area enclosed by the curve OMABO [y² = 9ax]:

Since, y² = 9ax

Therefore, y = \(3\sqrt{ax}\)

\(\\\boldsymbol{\Rightarrow }\) \(\boldsymbol{\int_{0}^{\frac{9a}{m^{2}}} y\;dx = \int_{0}^{\frac{9a}{m^{2}}}3\sqrt{ax}\;dx}\\\)

\(\\\boldsymbol{\Rightarrow }\) \(\boldsymbol{3\sqrt{a}\left [ \frac{2}{3}\times x^{\frac{3}{2}} \right ]_{0}^{\frac{9\;a}{m^{2}}}=3\sqrt{a}\times \frac{2}{3}\times \left ( \frac{9\;a}{m^{2}} \right )^{\frac{3}{2}}}\\\)

\(\\\boldsymbol{\Rightarrow }\) \(\boldsymbol{2\sqrt{a} \times 27\times a\sqrt{a}\times \frac{1}{m^{3}}=\frac{54\;a^{2}}{m^{3}}}\) unit²

Therefore, the Area enclosed by the curve OMABO \(=\frac{54\;a^{2}}{m^{3}}\) unit²

Now, the Area enclosed by the curve OAMO [y = mx]:

\(\\\boldsymbol{\Rightarrow }\) \(Area\;of \;\Delta OAM = \frac{1}{2}\times Base\times Altitude\)

\(\\\boldsymbol{\Rightarrow }\) \(\frac{1}{2}\times |OM|\times |AM|=\boldsymbol{\frac{1}{2}\times \frac{9\;a}{m^{2}}\times \frac{9\;a}{m}}\)

\(\\\boldsymbol{\Rightarrow }\) \(\boldsymbol{\frac{81\;a^{2}}{2\;m^{3}}}\) unit²

Therefore, the Area enclosed by the curve OAMO =\(\frac{81\;a^{2}}{2\;m^{3}}\) unit²

Now, the Area of region enclosed by the curve OABO = Area enclosed by the curve OMABO – Area enclosed by the curve OAMO

i.e. \(\frac{54\;a^{2}}{m^{3}}-\frac{81\;a^{2}}{2\;m^{3}} = \frac{27\;a^{2}}{2\;m^{3}}\) unit²

Therefore, the Area enclosed by the curve OABO = \(\frac{27\;a^{2}}{2\;m^{3}}\)unit²

 

Q.6: Find the area bounded by the curve whose equation is 3x² = 4y and the line 2y – 12 = 3x.

Sol:Based on formula given in Application of Integrals

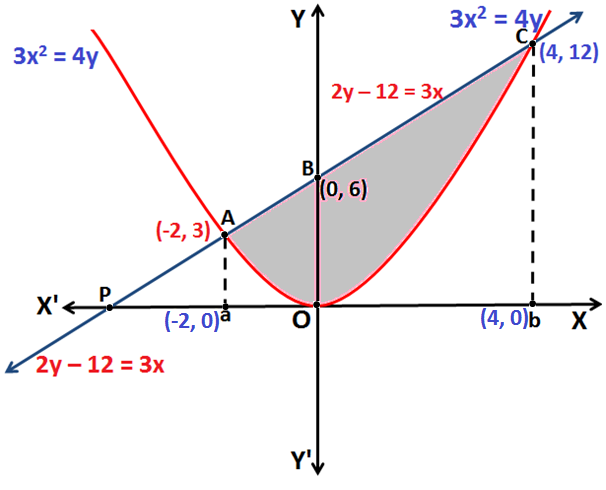
Equation 3x² = 4y represents a parabola, symmetrical about the y-axis as shown in the above figure.

The Area of the region bounded by parabola 3x² = 4y and the line 2y -12 = 3x is the Area enclosed under the curve ABC0A.

Since, the parabola 3x² = 4y and the line 3x = 2y – 12 intersect each other at points A and C, hence the coordinates of points A and C are given by:

Since, \(\;x=\frac{2y-12}{3}\)

\(\\\boldsymbol{\Rightarrow }\) \(3\left ( \frac{2y-12}{3} \right )^{2}=4y\;\;\;i.e. \;\;\;(2y-12)^{2}=12y\)

\(\\\boldsymbol{\Rightarrow }\) 4y² +144 – 48y – 12 y = 0

\(\\\boldsymbol{\Rightarrow }\) y² – 15y + 36 = 0

By splitting the middle term Method solutions of this quadratic equation are:

y² – (12+3)y + 36 = 0 \(\Rightarrow\) y(y – 12) –3(y – 12) = 0

\(\Rightarrow\) (y – 3) (y – 12) = 0

Therefore, y = 12 and y = 3 which gives x = 4 and x = -2 respectively.

Hence, the co-ordinates of point A and point C are (-2, 3) and (4, 12) respectively.

Since, 3x² = 4y

Therefore, y = \(\frac{3x^{2}}{4}\)

The Area of region bounded by the curve ABCOA = [Area of region aACba] – [Area of region OCbO + Area of region OAaO ]

The Area enclosed by the curve aACBa [2y – 12 = 3x]:

\(\\\boldsymbol{\Rightarrow }\) \(\boldsymbol{\int_{-2}^{4} y\;dx \Rightarrow \int_{-2}^{4}\frac{3x+12}{2}\;dx}\\\)

\(\\\boldsymbol{\Rightarrow }\) \(\boldsymbol{\frac{1}{2}\left | \frac{3x^{2}}{2}+ 12x \right |_{-2}^{4}}\\\)

\(\\\boldsymbol{\Rightarrow }\) \(\boldsymbol{\frac{1}{2}\left [ 24+48-6-(-24) \right ]=45}\) unit²

The Area enclosed by the curve OAaO [3x² = 4y]:

\(\boldsymbol{\Rightarrow }\) \(\boldsymbol{\int_{-2}^{0}\;y\;dx\;\Rightarrow \int_{-2}^{0} \frac{3x^{2}}{4}\;dx}\\\)

\(\\\boldsymbol{\Rightarrow }\) \(\boldsymbol{\frac{3}{4}\left | \frac{x^{3}}{3}\right |_{-2}^{0}}\\\)

\(\\\boldsymbol{\Rightarrow }\) \(\boldsymbol{\left | \frac{3}{4}(0-\frac{-8}{3}) \right |=2}\) unit²

The Area enclosed by the curve OCbO [3x² = 4y]:

\(\boldsymbol{\Rightarrow }\) \(\boldsymbol{\int_{0}^{4}\;y\;dx\;\Rightarrow \int_{0}^{4} \frac{3x^{2}}{4}\;dx}\\\)

\(\\\boldsymbol{\Rightarrow }\) \(\boldsymbol{\frac{3}{4}\left | \frac{x^{3}}{3}\right |_{0}^{4}}\\\)

\(\\\boldsymbol{\Rightarrow }\) \(\boldsymbol{\left | \frac{3}{4}(\frac{64}{3}-0) \right |=16}\) unit²

Now, the Area of region bounded by the curve ABCOA = [ Area of region aACba ] – [ Area of region OCbO + Area of region OAaO ]

\(\\\boldsymbol{\Rightarrow }\) 45 – [2 + 16] = 27 unit²

Therefore, the Area of shaded region ABCOA = 27 unit²

Q.7: Find the area enclosed by the curves {(x , y) : 6y ≥ x² and y = |x|}

Sol:Based on formula given in Application of Integrals

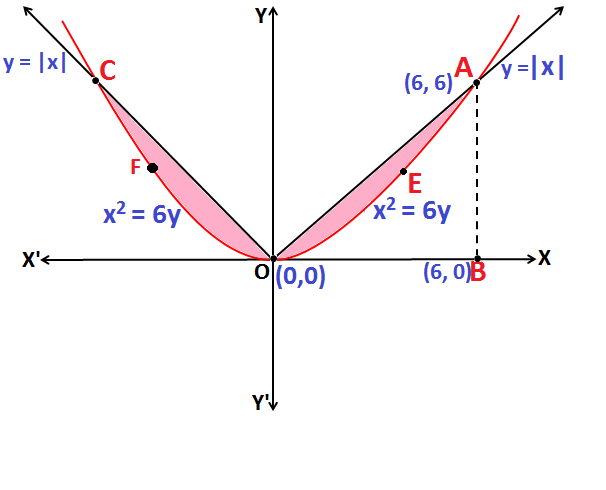
Equation x² = 6y represents a parabola, symmetrical about the y-axis as shown in the above figure.

The Area of the region bounded by the curve x² = 6y and y = |x| is 2(OAEO) i.e. (area OCFO+ area OAEO)

Now, Area of region OAEO = OABO – OEABO

Since, x² = 6y

Therefore, \(y=\frac{x^{2}}{6}\)

Now, the Area of region bounded by the curve OEABO:

\(\\\boldsymbol{\Rightarrow }\) \(\boldsymbol{\int_{0}^{6}y\;dx\;\Rightarrow \;\int_{0}^{6}\frac{x^{2}}{6}\;dx}\\\)

\(\\\boldsymbol{\Rightarrow }\) \(\boldsymbol{\frac{1}{6}\left | \frac{x^{3}}{3} \right |_{0}^{6}=12}\) unit²

Therefore, the Area of region bounded by the curve OEABO = 12 unit²

Now, the Area of region bounded by the curve OABO:

\(\\\boldsymbol{\Rightarrow }\) \(\boldsymbol{\int_{0}^{6}y\;dx\;\Rightarrow \;\int_{0}^{6}x\;dx}\)

\(\\\boldsymbol{\Rightarrow }\) \(\boldsymbol{\left | \frac{x^{2}}{2} \right |_{0}^{6}=18}\) unit²

Therefore, the Area of the region bounded by the curve OABO = 18 unit²

Now, Area of region OAEO = Area of region (OABO – OEABO)

\(\\\boldsymbol{\Rightarrow }\) 18 – 12 = 6 unit²

Therefore, the total Area of shaded region = 2 × 6 = 12 unit²

Q.8: Find the area enclosed by the sides of a triangle whose vertices have coordinates (3, 0) (5, 8) and (7, 5).

Sol:Based on formula given in Application of Integrals

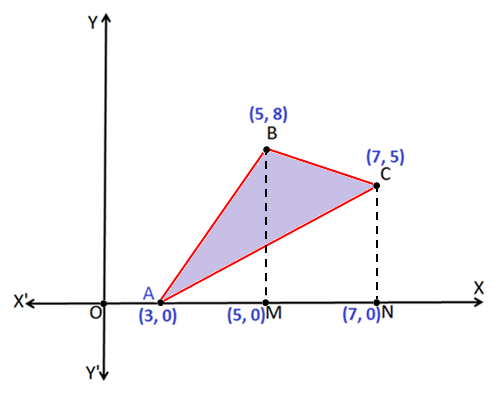
Form the above figure:

Let, A (3, 0), B (5, 8) and C (7, 5) be the vertices of triangle ABC.

Now, the equation of line AB:

Since, \((y-y_{1})=(x-x_{1})\times \left(\frac{y_{2}-y_{1}}{x_{2}-x_{1}}\right)\)

\(\boldsymbol{\Rightarrow }\) \((y-0)=(x-3)\times \left(\frac{8-0}{5-3}\right)\)

\(\boldsymbol{\Rightarrow }\) 2y = 8x – 24

\(\boldsymbol{\Rightarrow }\) y=4x-12

The Equation of line BC:

Since, \((y-y_{1})=(x-x_{1})\times \left(\frac{y_{2}-y_{1}}{x_{2}-x_{1}}\right)\)

\(\boldsymbol{\Rightarrow }\) \((y-8)=(x-5)\times \left(\frac{5-8}{7-5}\right)\)

\(\boldsymbol{\Rightarrow }\) 2y – 16 = -3x + 15

\(\boldsymbol{\Rightarrow }\) \(\boldsymbol{\Rightarrow y=\frac{31-3x}{2}}\)

The Equation of line AC:

Since, \((y-y_{1})=(x-x_{1})\times \left(\frac{y_{2}-y_{1}}{x_{2}-x_{1}}\right)\)

\(\boldsymbol{\Rightarrow }\) \((y-0)=(x-3)\times \left(\frac{5-0}{7-3}\right)\)

\(\boldsymbol{\Rightarrow }\) 4y=5x-15

\(\boldsymbol{\Rightarrow }\) \(\boldsymbol{\Rightarrow y=\frac{5x-15}{4}}\)

Now, the Area of triangle ABC = Area under the curve ABMA + Area under the curve MBCN – Area under the curve ACNA.

The Area under the curve ABMA [y = 4x – 12]:

\(\\\boldsymbol{\Rightarrow }\) \(\boldsymbol{\int_{3}^{5}y\;dx\;=\;\int_{3}^{5}(4x-12)\;dx}\)

\(\\\boldsymbol{\Rightarrow }\) \(\boldsymbol{\left [ \frac{4x^{2}}{2}-12x\right ]_{3}^{5}}\\\)

\(\\\boldsymbol{\Rightarrow }\) \(\boldsymbol{[50-60]-[18-36]=8}\)unit²

Therefore, Area under the curve ABMA = 8 unit²

The Area under the curve MBCN [2y + 3x = 31]:

\(\\\boldsymbol{\Rightarrow }\) \(\boldsymbol{\int_{5}^{7}y\;dx\;=\;\int_{5}^{7}\frac{31-3x}{2}\;dx}\)

\(\\\boldsymbol{\Rightarrow }\) \(\boldsymbol{\frac{1}{2}\times \left [ 31x-\frac{3x^{2}}{2}\right ]_{5}^{7}}\\\)

\(\\\boldsymbol{\Rightarrow }\) \(\boldsymbol{[\frac{217}{2}-\frac{147}{4}]-[\frac{155}{2}-\frac{75}{4}]=13}\) unit²

Therefore, Area under the curve MBCN = 13 unit²

The Area under the curve ACNA [4y = 5x – 15]:

\(\\\boldsymbol{\Rightarrow }\) \(\boldsymbol{\int_{3}^{7}y\;dx\;=\;\int_{3}^{7}\left ( \frac{5x-15}{4} \right )dx}\)

\(\\\boldsymbol{\Rightarrow }\) \(\boldsymbol{\left [ \frac{5x^{2}}{8}-\frac{15x}{4} \right ]_{3}^{7}}\\\)

\(\\\boldsymbol{\Rightarrow }\) \(\boldsymbol{\left [ \frac{245}{8}-\frac{105}{4} \right ]-\left [ \frac{45}{8}-\frac{45}{4} \right ]=10}\) unit²

Therefore, Area under the curve ACNA = 10 unit²

Now, Area of triangle ABC = Area under curve ABMA + Area under curve MBCN – Area under curve ACNA.

Therefore, the Area of triangle ABC = 8 + 13 – 10 = 11 unit²

Q.9: Find the area enclosed by the sides of a triangle whose equations are: 2x – 4 = y, – 2y = -3x + 6 and x – 3y = -5.

Sol:Based on formula given in Application of Integrals

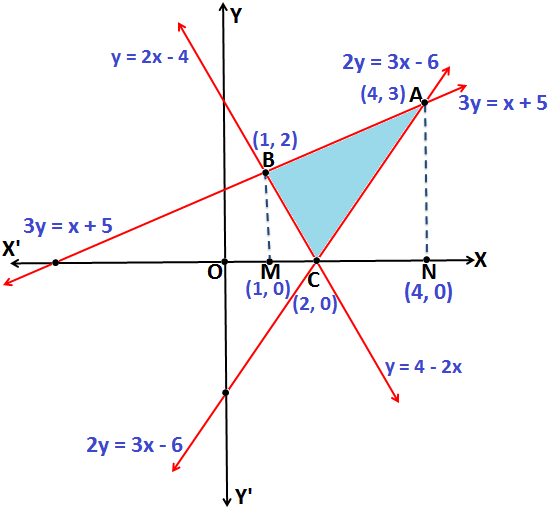
From the above figure:

The Equation of line AB: 3y = x + 5 . . . . . . (1)

The Equation of line BC: y = 4 – 2x . . . . . . (2)

The Equation of line AC: 2y = 3x – 6 . . . . . . (3)

From equation (1) and equation (2):

3(4 – 2x) = x + 5 i.e. x = 1, which gives y = 2

Therefore, the coordinates of point B are (1, 2)

From equation (2) and equation (3):

2(4 – 2x) = 3x – 6 i.e. x = 2 which gives y = 0

Therefore, the coordinates of point C are (2, 0).

From equation (1) and equation (3):

2y = 3(3y – 5) – 6 i.e. y = 3 which gives x = 4

Therefore, the coordinates of point A are (4, 3).

Now, the Area of triangle ABC = Area enclosed by the curve ABMNA – Area enclosed by the curve BMCB – Area enclosed by the curve ACNA

The Area under the curve ABMNA [3y = x + 5]:

\(\\\boldsymbol{\Rightarrow }\) \(\boldsymbol{\int_{1}^{4}y\;dx\;=\;\int_{1}^{4}\frac{x+5}{3}\;dx}\)

\(\\\boldsymbol{\Rightarrow }\) \(\boldsymbol{\left [ \frac{x^{2}}{6}+\frac{5x}{3} \right ]_{1}^{4}}\\\)

\(\\\boldsymbol{\Rightarrow }\) \(\boldsymbol{\frac{16}{6}+\frac{20}{3}-\frac{1}{6}-\frac{5}{3}=\frac{15}{2}}\) unit²

Therefore, the Area under the curve ABMNA \(=\frac{15}{2}\) unit²

The Area under the curve BMCB [y = 4 – 2x]:

\(\\\boldsymbol{\Rightarrow }\) \(\boldsymbol{\int_{1}^{2}y\;dx\;=\;\int_{1}^{2}(4-2x)\;dx}\)

\(\\\boldsymbol{\Rightarrow }\) \(\boldsymbol{\left [ 4x-x^{2} \right ]_{1}^{2}}\)

\(\\\boldsymbol{\Rightarrow }\) [8 – 4] – [4 – 1] =1 unit²

Therefore, the Area under the curve MBCN = 1 unit²

The Area under the curve ACNA [2y = 3x – 6]:

\(\\\boldsymbol{\Rightarrow }\) \(\boldsymbol{\int_{2}^{4}y\;dx\;=\;\int_{2}^{4}\frac{3x-6}{2}\;dx}\)

\(\\\boldsymbol{\Rightarrow }\) \(\boldsymbol{\left [ \frac{3x^{2}}{4}-\frac{6x}{2} \right ]_{2}^{4}}\\\)

\(\\\boldsymbol{\Rightarrow }\) \(\boldsymbol{\left [ \frac{3\times 16}{4}-\frac{6\times 4}{2} \right ]- \left [ \frac{3\times 4}{4}-\frac{6\times 2}{2} \right ]=3}\) unit²

Therefore, the Area under the curve ACNA = 3 unit²

The Area of triangle ABC = Area enclosed by the curve ABMNA – Area enclosed by the curve BMCB – Area enclosed by the curve ACNA

\(\\\boldsymbol{\Rightarrow }\) \(\frac{15}{2}-1-3 = 3.5\) unit²

Therefore, the Area of triangle ABC = 3.5 unit²

Q.10: Find the area enclosed by the curve 2x² = y and the line y = 2x + 12 and x – axis.

Sol:Based on formula given in Application of Integrals

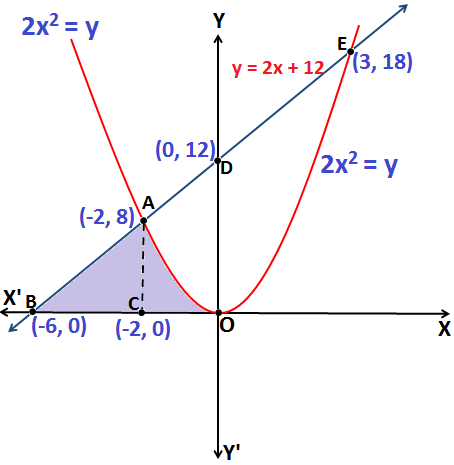
Equation 2x² = y represents a parabola, symmetrical about the y-axis as shown in the above figure.

The Area of the region bounded by parabola 2x² = y and the line y = 2x + 12 and x-axis is the Area enclosed under the curve ABCOA.

Since, the parabola 2x² = y and the line y = 2x + 12 intersect each other at points A and C, hence the coordinates of points A and C are given by:

Since, y = 2x + 12

\(\\\boldsymbol{\Rightarrow }\) 2x² = (2x+12)

\(\\\boldsymbol{\Rightarrow }\) x² – x – 6 = 0

By splitting the middle term Method solutions of this quadratic equation are:

x² – (3 – 2)x – 6 = 0 \(\Rightarrow\) x(x – 3) +2(x – 3) = 0

\(\Rightarrow\) (x – 3) (x + 2) = 0

Therefore, x = 3 and x = -2 which gives y = 18 and y = 8 respectively.

Hence, the co-ordinates of point E and point A are (3, 18) and (-2, 8) respectively.

Since, 2x² = y

Therefore, y = 2x²

The Area of region bounded by the curve ABCOA = [Area of region ACOA] + [Area of region ABC]

The Area enclosed by the curve ACOA [ 2x² = y ]:

\(\\\boldsymbol{\Rightarrow }\) \(\boldsymbol{\int_{-2}^{0}\;y\;dx\;\Rightarrow \int_{-2}^{0} 2x^{2}\;dx}\)

\(\\\boldsymbol{\Rightarrow }\) \(\boldsymbol{\left | \frac{2\;x^{3}}{3}\right |_{-2}^{0}}\)

\(\\\boldsymbol{\Rightarrow }\) \(\boldsymbol{\left |(0-\frac{-16}{3}) \right |=\frac{16}{3}}\) unit²

The Area enclosed by the curve ABC [ y = 2x + 12 ] :

\(\\\boldsymbol{\Rightarrow }\) \(\boldsymbol{Area\;of\;\Delta ABC=\frac{1}{2}\times Base\times Altitude}\)

\(\\\boldsymbol{\Rightarrow }\) \(\boldsymbol{\frac{1}{2}\times |BC|\times |AC|=\frac{1}{2}\times \left | 4 \right |\times |8|=16}\) unit²

The Area of region bounded by the curve ABCOA = [Area of region ACOA] + [Area of region ABC]

\(\Rightarrow \frac{16}{3}+16=\frac{64}{3}\) unit²

Therefore, the Area of shaded region ABCOA \(=\frac{64}{3}\)unit²

Q.11: Plot the curve y = |x + 4| and hence evaluate \(\int_{-9}^{0}|x+4|\;dx\)

Sol:Based on formula given in Application of Integrals

From the given equation the corresponding values of x and y are given in the following table.

X	-9	-8	-7	-6	-5	-4	-3	-2	-1	0	1	2	3
Y	5	4	3	2	1	0	1	2	3	4	5	6	7

Now, on using these values of x and y, we will plot the graph of y = |x + 4|

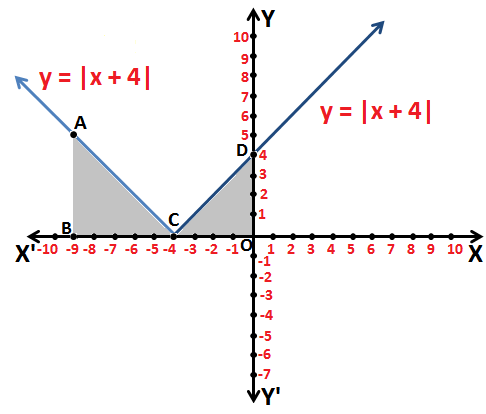
From the above graph, the required Area = the Area enclosed by the curve ABCA + the Area enclosed by the curve CDOC

\(\\\boldsymbol{\Rightarrow }\) \(\boldsymbol{\int_{-9}^{0}|x+4|\;dx+\int_{-9}^{-4}(x+4)\;dx+\int_{-4}^{0}(x+4)\;dx}\\\)

\(\\\boldsymbol{\Rightarrow }\) \(\boldsymbol{\left [ \left | \frac{x^{2}}{2}+4x \right | \right ]_{-9}^{-4}+\left [ \left | \frac{x^{2}}{2}+4x \right | \right ]_{-4}^{0}}\\\)

\(\\\boldsymbol{\Rightarrow }\) \(\boldsymbol{\left | 8-16-\frac{81}{2}+36 \right |+\left | 0-(8-16) \right |=\left | \frac{-25}{2} \right |+8}\)

\(\\\boldsymbol{\Rightarrow }\) \(\boldsymbol{\frac{41}{2}}\) unit²

Therefore, the area of shaded region = \(\frac{41}{2}\) unit²

 

 

Q.12: Find the area enclosed by the curve y = sin x between 0 ≤ x ≤ 2π

Sol:Based on formula given in Application of Integrals

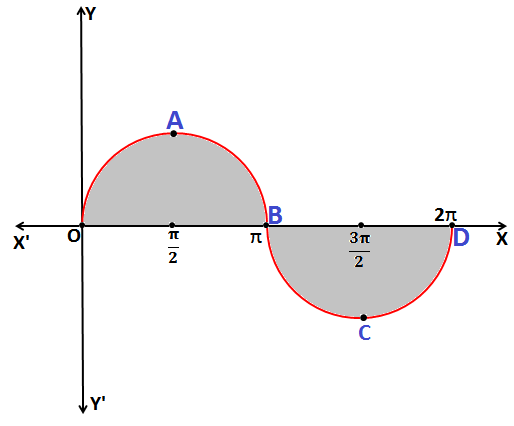
From the above figure, the required Area is represented by the curve OABCD.

Now, the Area bounded by the curve OABCD = the Area bounded by the curve OABO + the Area bounded by the curve BCDB

\(\\\boldsymbol{\Rightarrow }\) \(\boldsymbol{\int_{0}^{\pi } sin(x)\;dx+\left | \int_{\pi }^{2\pi } sin(x)\;dx\right |}\\\)

\(\\\boldsymbol{\Rightarrow }\) \(\boldsymbol{\left [ -cos(x)\right ]_{0}^{\pi }+\left | \left [ -cos (x) \right ] _{\pi }^{2\pi }\right |}\\\)

\(\\\boldsymbol{\Rightarrow }\) \(\boldsymbol{[-cos(\pi )+cos(0)]+\left | [-cos(2\pi )+cos(\pi )] \right |}\\\)

\(\boldsymbol{\Rightarrow }\) [1+1] + [ |– 1 – 1| ] unit²

Therefore, the area of shaded region = 4 unit²

Q.13: Find the area of smaller region enclosed by the curve \(\frac{x^{2}}{4}+\frac{y^{2}}{9} = 1\) and the line \(\frac{x}{2}+\frac{y}{3}=1\)

Sol:Based on formula given in Application of Integrals

The Equation \(\frac{x^{2}}{4}+\frac{y^{2}}{9} = 1\) represents an ellipse.

The Equation \(\frac{x}{2}+\frac{y}{3}=1\) represents a line with x and y intercepts as 2 and 3 respectively.

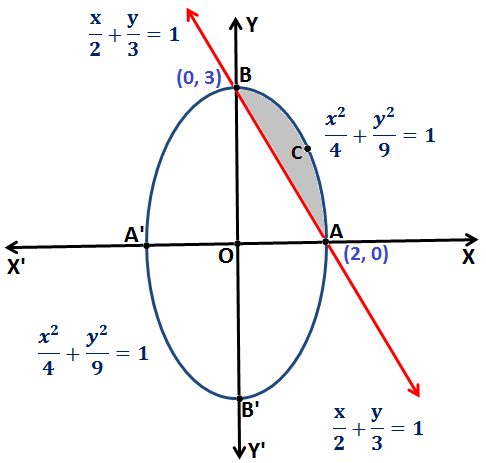
Since, \(\frac{x^{2}}{4}+\frac{y^{2}}{9} = 1\)

\(\\\boldsymbol{\Rightarrow }\) \(\frac{y^{2}}{9}=1-\frac{x^{2}}{4}\)

\(\\\boldsymbol{\Rightarrow }\) \(y=\frac{3}{2}\sqrt{4-x^{2}}\)

Therefore, the Area of smaller region enclosed by the Ellipse \(\frac{x^{2}}{4}+\frac{y^{2}}{9} = 1\) and the line \(\frac{x}{2}+\frac{y}{3}=1\) is represented by curve ACBA

Now, the Area enclosed by the curve ACBA = Area enclosed by the curve ACBOA – Area enclosed by the curve ABOA

Now, the Area enclosed by the curve ACBOA:

\(\boldsymbol{\int_{0}^{2} y\;dx\Rightarrow\frac{3}{2}\times \int_{0}^{2}\sqrt{2^{2}-(x)^{2}}\;dx}\\\)

Since, \(\ \int \sqrt{a^{2}-x^{2}}\;dx = \frac{x}{2}\sqrt{a^{2}-x^{2}}+\frac{a^{2}}{2}\sin^{-1}\frac{x}{a}\)

\(\\\boldsymbol{\Rightarrow }\) \(\boldsymbol{\frac{3}{2}\;\left [ \frac{x}{2}\sqrt{2^{2}-(x)^{2}}+\frac{4}{2}\sin^{-1}\frac{x}{2} \right ]_{0}^{2}}\\\)

\(\\\boldsymbol{\Rightarrow }\) \(\boldsymbol{\frac{3}{2}[\frac{2}{2}\sqrt{4-4}+2\sin^{-1}(1)-0]=\frac{3\pi }{2}}\) unit²

Therefore, the Area enclosed by the curve ACBOA = \(\boldsymbol{\frac{3\pi}{2}}\)unit²

Now, the Area enclosed by the curve ABOA:

\(\\\boldsymbol{\Rightarrow }\) \(\boldsymbol{Area \;of\;\Delta ABO = \frac{1}{2}\times AO\times BO}\)

\(\\\boldsymbol{\Rightarrow }\) \(\boldsymbol{\frac{1}{2}\times 2\times 3=3}\) unit²

Therefore, the Area enclosed by the curve ABOA = 3 unit²

Since, the Area enclosed by the curve ACBA = Area enclosed by the curve ACBOA – the Area enclosed by the curve ABOA

\(\\\boldsymbol{\Rightarrow }\) \(\frac{3\pi }{2}-3=\frac{3}{2}(\pi -2)\)unit²

Therefore, the Area of shaded region \(=\frac{3}{2}(\pi -2)\) unit²

Q.14: Find the area enclosed by the curve |x| + |y| = 2, by using the method of integration.

Sol: Based on formula given in Application of Integrals

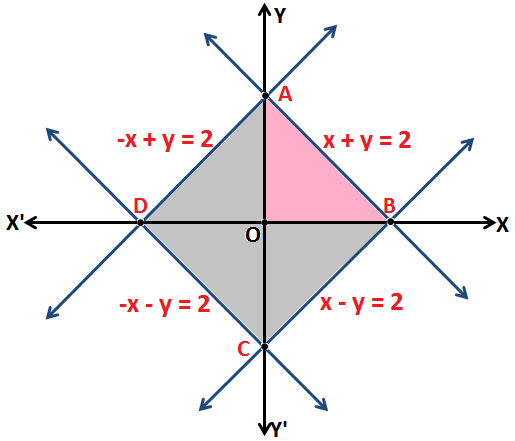
Equation |x| + |y| = 2 represent a region bounded by the lines:

x + y = 2 . . . . . . (1)

x – y = 2 . . . . . . (2)

-x + y = 2 . . . . . . (3)

-x – y = 2 . . . . . . (4)

From equations (1), (2), (3) and (4) we conclude that the curve intersects x-axis and y-axis axis at points A (0, 2), B (2, 0), C (0, -2) and D (-2, 0) respectively.

From the above figure:

Since, the curve is symmetrical to x-axis and y-axis. Therefore, the Area of region bounded by the curve ABCDA = 4 × Area of region bounded by the curve ABOA

Now, the Area of region bounded by the curve ABOA:

\(\\\boldsymbol{\Rightarrow }\) \(\boldsymbol{\int_{0}^{2}y\;dx=4\int_{0}^{2}(2-x)dx}\)

\(\\\boldsymbol{\Rightarrow }\) \(\boldsymbol{\left [ 2x-\frac{x^{2}}{2} \right ]_{0}^{2}=(4-2)=2}\\\) unit²

Therefore, the Area of region bounded by the curve ABOA = 2unit²

Since, the Area of region bounded by the curve ABCDA = 4 × Area of region bounded by the curve ABOA

Therefore, the Area of region bounded by the curve ABCDA = (2 × 4) = 8 unit²

Therefore, the Area of shaded region = 8 unit²

Q.15: Find the area which is exterior to curve x² = 2y and interior to curve x² + y² = 15.

Sol: Based on formula given in Application of Integrals

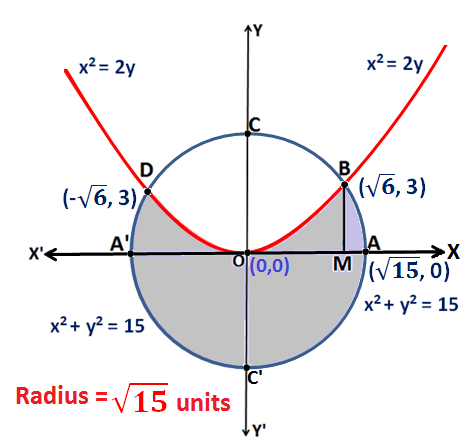
The Equation x² = 2y represents a parabola symmetrical about y-axis.

The Equation x² + y² = 15 represents a circle with centre (0, 0) and radius units.

Now, on substituting the equation of parabola in the equation of circle we will get:

(2y) + y² = 15 i.e. y² + 2y – 15 = 0

Now, by splitting the middle term method solutions of this quadratic equation are:

y² + (5 – 3)y – 15 = 0 \(\Rightarrow\) y(y + 5) – 3(y +5) = 0

\(\Rightarrow\) (y – 3) (y + 5) = 0

Neglecting y = -5 [gives absurd values of x]

Therefore, y = 3 which gives x = \(\pm \sqrt{6}\)

Hence, the coordinates of point B and point D are (\(\sqrt{6}\), 3) (\(-\sqrt{6}\), 3) respectively.

Now, the Area of region bounded by the curve BAC’A’DOB = 2 × (Area of region bounded by the curve OBMO + Area of region bounded by the curve BAMB+ Area of region bounded by the curve OAC’O)

Area of region bounded by the curve BAMB [ x ² + y² = 15 ]:

\(\\\boldsymbol{\Rightarrow }\) \(\boldsymbol{\int_{\sqrt{6}}^{\sqrt{15}}y\;dx=\int_{\sqrt{6}}^{\sqrt{15}}\sqrt{\left ( \sqrt{15} \right )^{2}-x^{2}}\;\;dx}\\\)

Since, \(\\\int \sqrt{a^{2}-b^{2}}\;dx = \frac{x}{2}\sqrt{a^{2}-x^{2}}+\frac{a^{2}}{2}\sin^{-1}\frac{x}{a}\\\)

\(\\\boldsymbol{\Rightarrow }\) \(\boldsymbol{\left [ \frac{x}{2}\sqrt{15- x^{2}}+\frac{15}{2}\sin^{-1}\frac{x}{\sqrt{15}} \right ]_{\sqrt{6}}^{\sqrt{15}}}\\\)

\(\\\boldsymbol{\Rightarrow }\) \(\boldsymbol{\left [ \frac {\sqrt{15}}{2}\times \sqrt{{15-15}}+\frac{15}{2}\sin^{-1}\frac{\sqrt{15}}{\sqrt{15}} \right ]-}\\\) \(\\\boldsymbol{\left [\frac {\sqrt{6}}{2}\times \sqrt{{15-6}}+\frac{15}{2}\sin^{-1}\frac{\sqrt{6}}{\sqrt{15}}\right]}\\\)

\(\\\boldsymbol{\Rightarrow }\) \(\boldsymbol{\left [ 0+\frac{15\pi }{4} \right ]-\left [\frac{3\sqrt{6}}{2}+\frac{15}{2}\sin^{-1}\frac{\sqrt{10}}{5}\right]}\\\)

\(\\\boldsymbol{\Rightarrow }\) \(\boldsymbol{\left [ \frac{15\pi }{4}=\frac{3\sqrt{6}}{2}-\frac{15}{2}\sin^{-1}\frac{\sqrt{10}}{5} \right ]}\)unit²

Area of region bounded by the curve OBMO [ x² = 2y ]:

\(\boldsymbol{\Rightarrow }\) \(\boldsymbol{\int_{0}^{\sqrt{6}}y\;dx=\int_{0}^{\sqrt{6}}\frac{x^{2}}{2}\;dx}\\\)

\(\\\boldsymbol{\Rightarrow }\) \(\boldsymbol{\left [ \frac{x^3}{6} \right ]_{0}^{\sqrt{6}}=\frac{6\sqrt{6}}{6}-0}\\\) = \(\boldsymbol{\sqrt{6}}\) unit²

Area of region bounded by the curve OAC’O:

\(\boldsymbol{\Rightarrow }\) \(\boldsymbol{\frac{Area\;of\;circle}{4}=\frac{\pi \times \left ( \sqrt{15} \right )^{2} }{4}}\\\) = \(\boldsymbol{\frac{15\pi }{4}}\)unit²

Now, the Area of region bounded by the curve BAC’A’DOB = 2 × (Area of region bounded by the curve OBMO + Area of region bounded by the curve BAMB + Area of region bounded by the curve OAC’O)

Therefore, the Area of region bounded by the curve BAC’A’DOB:

\(\boldsymbol{\Rightarrow }\) \(2\left [ \frac{15\pi }{4}-\frac{3\sqrt{6}}{2}-\frac{15}{2}\sin^{-1}\frac{\sqrt{10}}{5}+\sqrt{6} +\frac{15\pi }{4}\right ]\\\)

\(\\\boldsymbol{\Rightarrow }\) \(\boldsymbol{\left [ 15\pi -\sqrt{6}-15\left ( \sin^{-1}\frac{\sqrt{10}}{5} \right ) \right ]}\\\)unit²

Therefore, the Area of shaded region: \(\boldsymbol{ \left [ 15\pi -\sqrt{6}-15\left ( \sin^{-1}\frac{\sqrt{10}}{5} \right ) \right ]}\)unit²

Q.16: Find the area enclosed by the curve y = x³, x-axis and the lines x = -2 and x = 2.

Sol. Based on formula given in Application of Integrals

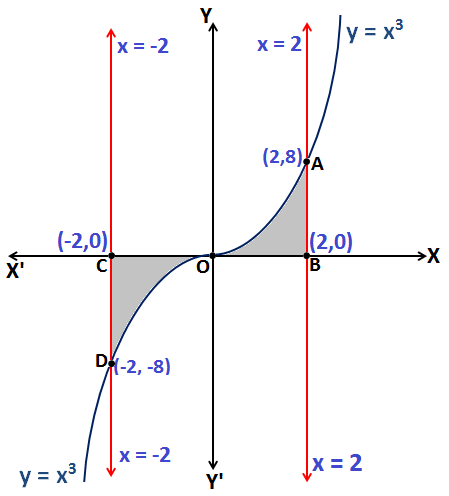
The Equation y = x³ represents a cubic parabola which intersects the line x = 2 and x = -2 at points A and D respectively

From the above figure, the required Area = Area enclosed by the curve ABOA + Area enclosed by the curve CODC

\(\\\boldsymbol{\Rightarrow }\) \(\boldsymbol{\int_{0}^{2}x^{3}\;dx+\left | \int_{-2}^{0}x^{3}\;dx \right |}\)

\(\\\boldsymbol{\Rightarrow }\) \(\boldsymbol{\left [ \frac{x^{4}}{4} \right ]_{0}^{2}+\left | \left [ \frac{x^{4}}{4} \right ]_{-2}^{0} \right |}\)

\(\\\boldsymbol{\Rightarrow }\) 4 – 0 + 0 + 4 =16 unit²

Therefore, the Area of shaded region = 16 unit²

Q.17: Find the area enclosed by the curve y = x|x|, y – axis and the lines y = -1 and y = 3.

Sol: Based on formula given in Application of Integrals

Now, y = x|x| is equal to [y = x²] when x > o

And y = x|x| is equal to [y = -x²] when x < o

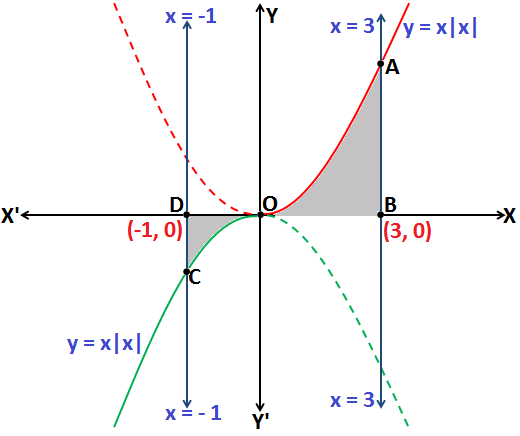
From the above figure, the required Area = Area enclosed by the curve ABOA + Area enclosed by the curve CODC

\(\\\boldsymbol{\Rightarrow }\) \(\boldsymbol{\int_{0}^{3}x^{2}\;dx+\left | \int_{-1}^{0}-x^{2}\;dx \right |}\\\)

\(\\\boldsymbol{\Rightarrow }\) \(\boldsymbol{\left [ \frac{x^{3}}{3}\right ]_{0}^{3}+\left | \left [ \frac{x^{3}}{3} \right ]_{-1}^{0} \right |}\\\)

\(\\\boldsymbol{\Rightarrow }\) \(\boldsymbol{9+\frac{1}{3}=\frac{28}{3}}\)unit²

Therefore, the area of shaded region \(=\frac{28}{3}\)unit²

Q.18: Find the area bounded by the curve y = Cos (x) and y = Sin (x) and y – axis, when [0 ≤ x ≤ \(\frac{\pi }{2}\)].

Sol: Based on formula given in Application of Integrals

y = Cos(x) . . . . . . . . (1)

y = Sin(x) . . . . . . . . . (2)

Now, from equation (1) and equation (2):

Cos (x) = Sin (x) \(\Rightarrow\) Cos (x) = Cos \(\left [ \frac{\pi }{2}-x \right ]\)

\(\Rightarrow\) x = \(\left [ \frac{\pi }{2}-x \right ]\) \(\Rightarrow\) x = \(\frac{\pi }{4}\)

Therefore, the coordinates of point A are: \(\left ( \frac{\pi }{4},\frac{1}{\sqrt{2}} \right )\)

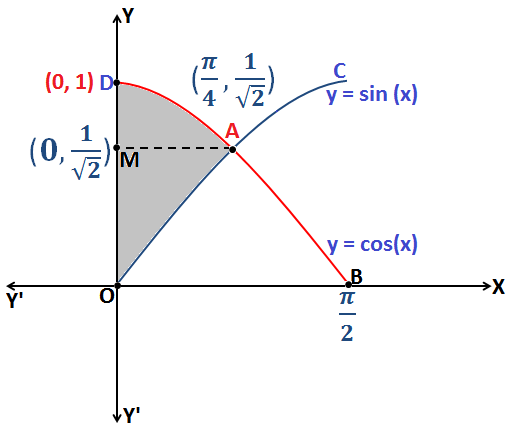
Now, from the above figure:

The required Area = Area enclosed by the curve ADMA + Area enclosed by the curve AMOA

\(\\\boldsymbol{\Rightarrow }\) \(\boldsymbol{\int_{0}^{\frac{1}{\sqrt{2}}}sin^{-1}y\;dy+ \int_{\frac{1}{\sqrt{2}}}^{1}cos^{-1}y\;dy}\\\)

Since, \(\int \sin^{-1}y\;dy= y\sin^{-1}y+\sqrt{1-y^{2}}\\\)

And, \(\\\int \cos^{-1}y\;dy= y \cos^{-1}y-\sqrt{1-y^{2}}\)

\(\\\boldsymbol{\Rightarrow }\) \(\boldsymbol{\int_{0}^{\frac{1}{\sqrt{2}}}sin^{-1}y\;dy+ \int_{\frac{1}{\sqrt{2}}}^{1}cos^{-1}y\;dy}\)

\(\\\boldsymbol{\Rightarrow }\) \(\boldsymbol{\left [ y\sin^{-1}y+\sqrt{1-y^{2}} \right ]_{0}^{\frac{1}{\sqrt{2}}}+\left [ y\cos^{-1}y-\sqrt{1-y^{2}} \right ]_{\frac{1}{\sqrt{2}}}^{1}}\)

\(\\\boldsymbol{\Rightarrow }\) \(\boldsymbol{\left [ \frac{1}{\sqrt{2}}\times \frac{\pi }{4}+\frac{1}{\sqrt{2}}-(0+1) \right ]+\left [ 0-\left ( \frac{1}{\sqrt{2}}\times \frac{\pi }{4}-\frac{1}{\sqrt{2}} \right ) \right ]}\\\)

\(\\\boldsymbol{\Rightarrow }\) \(\boldsymbol{\left [\sqrt{2}-1 \right ]}\)unit²

Therefore, the Area of shaded region = \(\left [\sqrt{2}-1 \right ]\)unit²

Q.20: Find the area which is exterior to curve y² = 6x and interior to curve x² + y² = 16.

Sol: Based on formula given in Application of Integrals

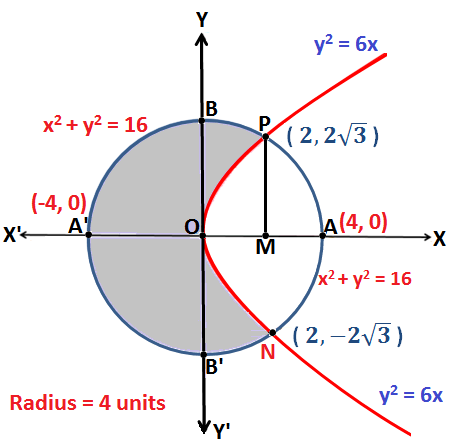
The Equation y² = 6x represents a parabola symmetrical about x – axis.

The Equation x² + y² = 16 represents a circle with centre (0, 0) and radius 4 units.

Now, on substituting the equation of parabola in the equation of circle we will get:

x² + (6x) = 16 i.e. x² + 6x – 16 = 0

Now, by splitting of middle term method solutions of this quadratic equation are:

x² + (8 – 2)x – 16 = 0 \(\Rightarrow\) x(x + 8) – 2(x + 8) = 0

\(\Rightarrow\) (x – 2) (x + 8) = 0

Neglecting x = -8 [gives absurd values of y]

Therefore, x = 2 which gives y = \(\pm 2\sqrt{3}\)

Hence, the coordinates of point B and point D are (2, \(2\sqrt{3}\)) (2, \(-2\sqrt{3}\)) respectively.

Now, the Area of region bounded by the curve PBA’B’NOP = 2 × (Area of region bounded by the curve BPMOB – Area of region bounded by the curve POMP + Area of region bounded by the curve BOA’B)

Area of region bounded by the curve BPMOB [x ² + y² = 16]:

\(\\\boldsymbol{\Rightarrow }\) \(\boldsymbol{\int_{0}^{2}y\;dx=\int_{0}^{2}\sqrt{\left ( 4\right )^{2}-x^{2}}\;\;dx}\\\)

Since, \(\\\int \sqrt{a^{2}-b^{2}}\;dx = \frac{x}{2}\sqrt{a^{2}-x^{2}}+\frac{a^{2}}{2}\sin^{-1}\frac{x}{a}\)

\(\\\boldsymbol{\Rightarrow }\) \(\boldsymbol{\left [ \frac{x}{2}\sqrt{16- x^{2}}+\frac{16}{2}\sin^{-1}\frac{x}{4} \right ]_{0}^{2}}\\\)

\(\\\boldsymbol{\Rightarrow }\) \(\boldsymbol{\left [ \frac{2}{2}\times \sqrt{{16-4}}+8\times \sin^{-1}\frac{1}{2} \right ]-0}\\\)

\(\\\boldsymbol{\Rightarrow }\) \(\boldsymbol{\left [ 2\sqrt{3}+\frac{8\times \pi }{6} \right ]=\left [ 2\sqrt{3}+\frac{4\pi }{3} \right ]}\\\)unit²

Therefore, Area of region bounded by the curve BPMOB = \(\left [ 2\sqrt{3}+\frac{4\pi }{3} \right ]\)unit²

Area of region bounded by the curve POMP [y² = 6x]:

\(\\\boldsymbol{\Rightarrow }\) \(\boldsymbol{\int_{0}^{2}y\;dx=\int_{0}^{2}\sqrt{6x}\;dx}\\\)

\(\\\boldsymbol{\Rightarrow }\) \(\left [ \frac{\sqrt{6}\times 2}{3}\times x^\frac{3}{2} \right ]_{0}^{2}=\frac{2\sqrt{6}}{3}\times 2\sqrt{2}-0\\\)

\(\\\boldsymbol{\Rightarrow }\) \(\frac{8\sqrt{3}}{3}\)unit²

Therefore, Area of region bounded by the curve POMP : \(\frac{8\sqrt{3}}{3}\)unit²

Area of region bounded by the curve BOA’B:

\(\\\boldsymbol{\Rightarrow \frac{Area\;of\;circle}{4}=\frac{\pi \times \left ( 4 \right )^{2} }{4}}\\\)

\(\\\boldsymbol{\Rightarrow }\) 4π unit²

Therefore, Area of region bounded by the curve BOA’B = 4π unit²

Now, the Area of region bounded by the curve PBA’B’NOP = 2 × (Area of region bounded by the curve BPMOB – Area of region bounded by the curve POMP + Area of region bounded by the curve BOA’B)

Therefore, the Area of region bounded by the curve PBA’B’NOP:

\(\\\boldsymbol{\Rightarrow }\) \(2\left [2\sqrt{3}+\frac{4\pi }{3}-\frac{8\sqrt{3}}{3}+4\pi \right ]\\\)

\(\\\boldsymbol{\Rightarrow }\) \(\boldsymbol{\left [ \frac{32\pi }{3}-\frac{4\sqrt{3}}{3} \right ]=\frac{4}{3}\times \left [ 8\pi -\sqrt{3} \right ]}\\\)unit²

Therefore, the Area of shaded region = \(\frac{4}{3}\times \left [ 8\pi -\sqrt{3} \right ]\)unit²

Q.21: Find the area bounded by the curve y = Cos (x) and y = Sin (x) and x – axis, when [0 ≤ x ≤ ].

Sol:Based on formula given in Application of Integrals

y = Cos(x) . . . . . . . . (1)

y = Sin(x) . . . . . . . . . (2)

Now, from equation (1) and equation (2):

Cos (x) = Sin (x) \(\Rightarrow\) Cos (x) = Cos \(\left [ \frac{\pi }{2}-x \right ]\\\)

\(\\\Rightarrow\) x = \(\left [ \frac{\pi }{2}-x \right ]\\\) \(\\\Rightarrow\) x = \(\frac{\pi }{4}\)

Therefore, the coordinates of point A are: \(\left ( \frac{\pi }{4},\frac{1}{\sqrt{2}} \right )\)

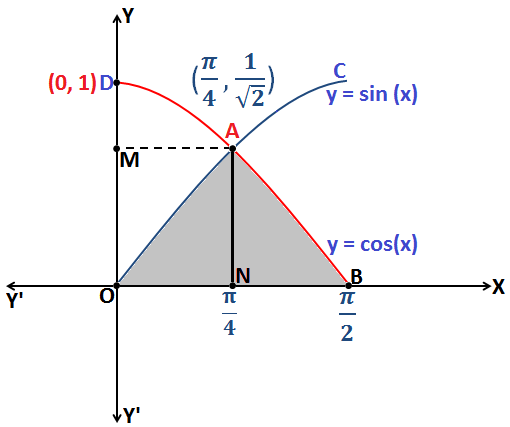
Now, from the above figure:

The required Area = Area enclosed by the curve AONA + Area enclosed by the curve ANBA

\(\\\boldsymbol{\Rightarrow }\) \(\boldsymbol{\left [ -cos(x) \right ]_{0}^{\frac{\pi }{4}}+[sin (x)]_{\frac{\pi }{4}}^{\frac{\pi }{2}}}\\\)

\(\\\boldsymbol{\Rightarrow }\) \(\boldsymbol{\left [ -cos\frac{\pi }{4}+cos(0)+sin\frac{\pi }{2}-sin\frac{\pi }{4}\right ]}\\\)

\(\\\boldsymbol{\Rightarrow }\) \(\boldsymbol{\left [ \frac{-1}{\sqrt{2}}+1+1-\frac{1}{\sqrt{2}} \right ]=[2-\sqrt{2}\;]}\)unit²

Therefore, the Area of shaded region \( = [2-\sqrt{2}\;]\)unit²

Previous

Next