NCERT Class 12 Chapter – 9 : Differential Equations
Exercise : 9.1
Q.1: Find the degree and order of the differential equation \(\frac{\mathrm{d} ^{4}y}{\mathrm{d} x^{4}}\)+sin (ym) = 0.
Solution: Based on the formula given under DIFFERENTIAL EQUATIONS
\(\frac{\mathrm{d} ^{4}y}{\mathrm{d} x^{4}}\) + sin (y”’) = 0
y”” + sin (y”’) = 0
y”” is the highest order derivative present in the differential equation.
Therefore, the order is four.
The given differential equation is not a polynomial equation in its derivatives. Hence, its degree is not defined.
Q.2: Find the degree and order of differential equation y’ + 5y = 0
Solution:Based on the formula given under DIFFERENTIAL EQUATIONS
Given: y’ + 5y = 0
y’ is the highest order derivative present in the differential equation.
Therefore, the order is one.
The given differential equation is a polynomial equation in y’. The highest degree derivative present in the differential equation is y’.
Therefore, the degree is one.
Q.3: Find the degree and order of differential equation \((\frac{\mathrm{d} s}{\mathrm{d} t})^{4}+3s\frac{\mathrm{d}^{2} s}{\mathrm{d} t}=0\).
Solution:Based on the formula given under DIFFERENTIAL EQUATIONS
\((\frac{\mathrm{d} s}{\mathrm{d} t})^{4}+3s\frac{\mathrm{d}^{2} s}{\mathrm{d} t}=0\)\(\frac{d^{2}s}{dt^{2}}\) is the highest order derivative present in the differential equation.
Therefore, the order is two.
The given differential equation is a polynomial equation in \(\frac{d^{2}s}{dt^{2}}\) and \(\frac{ds}{dt}\).The power raised to \(\frac{d^{2}s}{dt^{2}}\) is 1.
Hence, its degree is one.
Q.4: Find the degree and order of differential equation \((\frac{d^{2}y}{dx^{2}})^{2}+cos(\frac{dy}{dx})=0\).
Solution:Based on the formula given under DIFFERENTIAL EQUATIONS
\((\frac{d^{2}y}{dx^{2}})^{2}+cos(\frac{dy}{dx})=0\)\(\\\frac{d^{2}y}{dx^{2}}\) is the highest order derivative present in the differential equation.
Therefore, the order is two.
The given differential equation is not a polynomial equation in its derivatives. Hence, its degree is not defined.
Q.5: Find the degree and order of differential equation \(\frac{d^{2}y}{dx^{2}} =\cos 3x+\sin 3x\)
Solution:Based on the formula given under DIFFERENTIAL EQUATIONS
\(\frac{d^{2}y}{dx^{2}} =\cos 3x+\sin 3x\\ \\ \Rightarrow \frac{d^{2}y}{dx^{2}}-\cos 3x-\sin 3x=0\)\(\frac{d^{2}y}{dx^{2}}\) is the highest order derivative present in the differential equation.
Therefore, the order is two.
It is a polynomial equation in \(\frac{d^{2}y}{dx^{2}}\) and the power raised to \(\frac{d^{2}y}{dx^{2}}\) is 1.
Hence, its degree is one.
Q.6: Find the degree and order of differential equation (y”’)2 + (y”)3 + (y’)4+ y5 = 0
Solution: Based on the formula given under DIFFERENTIAL EQUATIONS(y”’)2 + (y”)3 + (y’)4+ y5 = 0
y”’ is the highest order derivative present in the differential equation.
Therefore, the order is three.
It is a polynomial equation in y”’, y” and y’.
The power of y”’ is 2.
Hence, its degree is 2.
Q.7: Find the degree and order of differential equation y”’ + 2y” + y’ = 0.
Solution: Based on the formula given under DIFFERENTIAL EQUATIONS
Given: y”’ + 2y” + y’ = 0.
y”’ is the highest order derivative present in the differential equation.
Therefore, the order is three.
It is a polynomial equation in y”’, y”, and y’.
The power of y”’ is 1.
Hence, its degree is 1.
Q.8: Find the degree and order of differential equation y’ + y = ex
Solution: Based on the formula given under DIFFERENTIAL EQUATIONSy’ + y = ex
\(\boldsymbol{\Rightarrow }\) y’ + y – ex = 0
y’ is the highest order derivative present in the differential equation.
Therefore, the order is one.
It is a polynomial equation in y’.
The power raised to y”’ is 1.
Hence, its degree is 1.
Q.9: Find the degree and order of differential equation y” + (y’)2 +2y = 0.
Solution:Based on the formula given under DIFFERENTIAL EQUATIONS
y” + (y’)2 +2y = 0
y” is the highest order derivative present in the differential equation.
Therefore, the order is two.
It is a polynomial equation in y” + y’.
The power raised to y” is 1.
Hence, its degree is 1.
Q.10: The degree of differential equation \((\frac{d^{2}y}{dx^{2}})+(\frac{dy}{dx})^{2}+\sin (\frac{dy}{dx})+1=0\) is:
(i) 3
(ii) 2
(iii) 1
(iv) not defined
Solution: Based on the formula given under DIFFERENTIAL EQUATIONS
\((\frac{d^{2}y}{dx^{2}})+(\frac{dy}{dx})^{2}+\sin (\frac{dy}{dx})+1=0\)The given differential equation is not a polynomial equation in its derivatives. Hence, its degree is not defined.
Hence, the answer is (iv).
Q.11: The degree of differential equation: \(2x^{2}\;\frac{d^{2}y}{dx^{2}}-3\frac{dy}{dx}+y=0\)is:
(i) 2
(ii) 1
(iii) 0
(iv) not defined
Solution:
\(\frac{d^{2}y}{dx^{2}}\) is the highest order derivative present in the differential equation.
Therefore, the order is two.
Hence, the correct answer is (i).
Exercise-9.2
Q.1: y = ex + 1; y” – y’ = 0
Solution: Based on the formula given under DIFFERENTIAL EQUATIONS
y = ex + 1
Differentiate both the sides with respect to x, we get:
\(\frac{dy}{dx}=\frac{d}{dx}(e^{x}+1)\\\)\(\Rightarrow\) y’ = ex . . . . . . . . . . . . . . (1)
Now, differentiate equation (1) with respect to x, we get:
\(\frac{d}{dx}(y^{‘})=\frac{d}{dx}(e^{x})\\\)\(\\\boldsymbol{\rightarrow }\) y” = ex
Substituting the values of y’ and y” in the given differential equation, we get the L.H.S. as:
y” – y’ = ex – ex = 0 = R.H.S
Thus, the given function is the solution of the corresponding differential equation.
Q.2: y = x2 + 2x + C; y’ – 2x – 2 = 0
Solution: Based on the formula given under DIFFERENTIAL EQUATIONS
y = x2 + 2x + C
Differentiate both the sides with respect to x, we get:
\(y^{‘}=\frac{d}{dx}(x^{2}+2x+C)\\\)\(\\\boldsymbol{\rightarrow }\) y’ = 2x + 2
Substituting the values of y’ in the given differential equation, we get the L.H.S. as:
y’ – 2x – 2 = 2x + 2 – 2x – 2 = 0 = R.H.S
Hence, the given function is the solution of the corresponding differential equation.
Q.3: y = cos x + C; y’ + sin x = 0
Solution: Based on the formula given under DIFFERENTIAL EQUATIONS
y = cos x + C
Differentiate both the sides with respect to x, we get:
y’ = \(\frac{d}{dx}\)(cos x + C )
\(\\\boldsymbol{\rightarrow }\) y’ = – sin x
Substituting the values of y’ in the given differential equation, we get the L.H.S. as:
y’ + sin x = -sin x + sin x = 0 = R.H.S.
Hence, the given function is the solution of the corresponding differential equation.
Q.4: y = \(\sqrt{1+x^{2}}\); y’ = \(\frac{xy}{1+x^{2}}\)
Solution: Based on the formula given under DIFFERENTIAL EQUATIONS
\(y=\sqrt{1+x^{2}}\)Differentiate both the sides with respect to x, we get:
y’ = \(\frac{d}{dx}(\sqrt{1+x^{2}})\)
y’ = \(\frac{1}{2\sqrt{1+x^{2}}}.\frac{d}{dx}(1+x^{2})\)
y’ = \(\frac{2x}{2\sqrt{1+x^{2}}}\)
y’ = \(\frac{x}{\sqrt{1+x^{2}}}\)
y‘ = \(\frac{x}{1+x^{2}}\times \sqrt{1+x^{2}}\)
y’ = \(\frac{x}{1+x^{2}}.y\)
y’ = \(\frac{xy}{1+x^{2}}\)
Therefore, L.H.S = R.H.S
Hence, the given function is the solution of the corresponding differential equation.
Q.5: y = Ax; xy’ = y (x ≠ 0)
Solution: Based on the formula given under DIFFERENTIAL EQUATIONS
Differentiate both the sides with respect to x, we get:
\(y^{‘}=\frac{d}{dx}(Ax)\\ \\ \Rightarrow y^{‘}=A\)Substituting the values of \(y^{‘}\) in the given differential equation, we get the L.H.S. as:
\(xy^{‘}=x.A=Ax=y=R.H.S.\)Hence, the given function is the solution of the corresponding differential equation.
Q.6. \(y=x\sin x\;:\;xy^{‘}=y+x\sqrt{x^{2}-y^{2}}(x\neq 0\:and\:x>y\:or\:x<-y)\)
Solution: Based on the formula given under DIFFERENTIAL EQUATIONS
y=x sin x
Differentiate both the sides with respect to x, we get:
\(y^{‘}=\frac{d}{dx}(x\sin x)\\ \\ \Rightarrow y^{‘}=\sin x.\frac{d}{dx}(x)+x.\frac{d}{dx}(\sin x)\\ \\ \Rightarrow y^{‘}=\sin x+x\cos x\)Substitute the value of \(y^{‘}\) in the given differential equation, we get:
L.H.S = \(xy^{‘}=x(\sin x+x\cos x )\\ \\ =x\sin x+x^{2}\cos x \\ \\ =y+x^{2}.\sqrt{1-\sin ^{2}x}\\ \\ =y+x^{2}\sqrt{1-(\frac{y}{x})^{2}}\\ \\ =y+x\sqrt{y^{2}-x^{2}}\)=R.H.S.
Hence, the given function is the solution of the corresponding differential equation.
Q.7. \(xy=log\, y+C\::\:y^{‘}=\frac{y^{2}}{1-xy}(xy\neq 1)\)
Solution: Based on the formula given under DIFFERENTIAL EQUATIONS
\(xy=log \, y+C\)Differentiate both the sides with respect to x, we get:
\(\frac{d}{dx}(xy)=\frac{d}{dx}(log \, y)\\ \\ \Rightarrow y.\frac{d}{dx}(x)+x.\frac{dy}{dx}=\frac{1}{y}\frac{dy}{dx}\\ \\ \Rightarrow y+xy^{‘}=\frac{1}{y}y^{‘}\\ \\ \Rightarrow y^{2}+xy\,y^{‘}=y^{‘}\\ \\ \Rightarrow (xy-1)y^{‘}=-y^{2}\\ \\ \Rightarrow y^{‘}=\frac{y^{2}}{1-xy}\)Therefore L.H.S = R.H.S
Hence, the given function is the solution of the corresponding differential equation.
Q.8. \(y-\cos y=x\::\:(y\sin y+\cos y+x)y^{‘}=y\)
Solution: Based on the formula given under DIFFERENTIAL EQUATIONS
\(y-\cos y=x\) ………..(1)
Differentiate both the sides with respect to x, we get:
\(\frac{dy}{dx}-\frac{d}{dx}(\cos y)=\frac{d}{dx}(x)\\ \\ \Rightarrow y^{‘}+\sin y.y^{‘}=1\\ \\ \Rightarrow y^{‘}(1+\sin y)=1\\ \\ \Rightarrow y^{‘}=\frac{1}{1+\sin y}\)Substitute the value of \(y^{‘}\) in the given differential equation, we get:
L.H.S = \((y\sin y+\cos y+x)y^{‘}\\ \\ =(y\sin y+\cos y+y-\cos y)\times \frac{1}{1+\sin y}\\ \\ =y(1+\sin y).\frac{1}{1+\sin y}\\ \\ =y\\ \\ =R.H.S.\)
Hence, the given function is the solution of the corresponding differential equation.
Q.9: \(x+y=\tan ^{-1}y\::\:y^{2}y^{‘}+y^{2}+1=0\)
Solution: Based on the formula given under DIFFERENTIAL EQUATIONS \(x+y=\tan ^{-1}y\)
Differentiate both the sides with respect to x, we get:
\(\frac{d}{dx}(x+y)=\frac{d}{dx}(\tan ^{-1}y)\\ \\ \Rightarrow 1+y^{‘}=[\frac{1}{1+y^{2}}]y^{‘}\\ \\ \Rightarrow y^{‘}[\frac{1}{1+y^{2}}-1]=1\\ \\ \Rightarrow y^{‘}[\frac{1-(1+y^{2})}{1+y^{2}}]=1\\ \\ \Rightarrow y^{‘}[\frac{-y^{2}}{1+y^{2}}]=1\\ \\ \Rightarrow y^{‘}=\frac{-(1+y^{2})}{y^{2}}\)Substitute the value of \(y^{‘}\) in the given differential equation, we get:
L.H.S = \(y^{2}y^{‘}+y^{2}+1=y^{2}[\frac{-(1+y^{2})}{y^{2}}]+y^{2}+1\\ \\ =-1-y^{2}+y^{2}+1\\ \\ =0\\ \\ =R.H.S.\)
Hence, the given function is the solution of the corresponding differential equation.
Q.10: \(y=\sqrt{a^{2}-x^{2}}x\in (-a,a)\: :\: x+y\frac{dy}{dx}=0(y\neq 0)\)
Solution: Based on the formula given under DIFFERENTIAL EQUATIONS
\(y=\sqrt{a^{2}-x^{2}}\)Differentiate both the sides with respect to x, we get:
\(\frac{dy}{dx}=\frac{d}{dx}(\sqrt{a^{2}-x^{2}})\\ \\ \Rightarrow \frac{dy}{dx}=\frac{1}{2\sqrt{a^{2}-x^{2}}}.\frac{d}{dx}(a^{2}-x^{2})\\ \\ =\frac{1}{2\sqrt{a^{2}-x^{2}}}(-2x)\\ \\ =\frac{-x}{\sqrt{a^{2}-x^{2}}}\)Substitute the value of \(\frac{dy}{dx}\)in the given differential equation, we get:
L.H.S = \(x+y\frac{dy}{dx}=x+\sqrt{a^{2}-x^{2}}\times \frac{-x}{\sqrt{a^{2}-x^{2}}}\\ \\ =x-x\\ \\ =0\\ \\ R.H.S.\)
Hence, the given function is the solution of the corresponding differential equation.
Q.11: The numbers of arbitrary constants in the general solution of a differential equation of fourth order are:
(i) 0
(ii) 2
(iii) 3
(iv) 4
Solution: Based on the formula given under DIFFERENTIAL EQUATIONS
We know that, number of constants in the general solution of a differential equation of order n is equal to its order.
Therefore, the number of constants in the general equation of fourth order differential equation is four.
Therefore, (iv) is the correct answer.
Q.12: The numbers of arbitrary constants in the particular solution of a differential equation of third order are:
(i) 3
(ii) 2
(iii) 1
(iv) 0
Solution: Based on the formula given under DIFFERENTIAL EQUATIONS
In a particular solution of a differential equation, there are no arbitrary constants. Hence, the correct answer is (iv).
Exercise-9.3
Q.1: \(\frac{x}{a}+\frac{y}{b}=1\)
Solution:
\(\frac{x}{a}+\frac{y}{b}=1\)Differentiate both the sides w.r.t x, we get:
\(\frac{1}{a}+\frac{1}{b}\frac{dy}{dx}=0\\ \\ \Rightarrow \frac{1}{a}+\frac{1}{b}y^{’}=0\)Again, differentiate both the sides w.r.t x, we get:
\(0+\frac{1}{b}y^{’’}=0\\ \\ \Rightarrow \frac{1}{b}y^{’’}=0\\ \\ \Rightarrow y^{’’}=0\)Hence, the required differential equation of the given curve is \(y^{’’}=0\).
Q.2: \(y^{2}=a(b^{2}-x^{2})\)
Solution: Based on the formula given under DIFFERENTIAL EQUATIONS
\(y^{2}=a(b^{2}-x^{2})\)Differentiate both the sides w.r.t x, we get:
\(2y\frac{dy}{dx}=a(-2x)\\ \\ \Rightarrow 2yy^{’}=-2ax\\ \\ \Rightarrow yy^{’}=-ax\) . . . . . . . . . . . . (1)
Again, differentiate both the sides w.r.t x, we get:
\(y^{’}.y^{’}+yy^{’’}=-a\\ \\ \Rightarrow (y^{’})^{2}+yy^{’’}=-a\)….(2)
Divide equation (2) by equation(1), we get:
\(\frac{(y^{’})^{2}+yy^{’’}}{yy^{’}}=\frac{-a}{-ax}\\ \\ \Rightarrow xyy^{’’}+x(y^{’})^{2}-yy^{’’}=0\)This is the required differential equation of the given curve.
Q.3: \(y=ae^{3x}+be^{-2x}\)
Solution: Based on the formula given under DIFFERENTIAL EQUATIONS
\(y=ae^{3x}+be^{-2x}\) ………….(1)
Differentiate both the sides w.r.t x, we get:
\(y^{’}=3ae^{3x}-2be^{-2x}\: \: \: \: \: ……(2)\)Again, differentiate both the sides w.r.t x, we get:
\(y^{’’}=9ae^{3x}+4be^{-2x}\: \: \: \: \: ……(3)\)Multiply equation(1) with 2 and then add it to equation (2), we get:
\((2ae^{3x}+2be^{-2x})+(3ae^{3x}-2be^{-2x})=2y+y^{’}\\ \\ \Rightarrow 5ae^{3x}=2y+y^{’}\\ \\ \Rightarrow ae^{3x}=\frac{2y+y^{’}}{5}\)Now, multiplying equation (1) with 3 and subtracting equation (2) from it, we get:
\((3ae^{3x}+3be^{-2x})-(3ae^{3x}-2be^{-2x})=3y-y^{’}\\ \\ \Rightarrow 5be^{-2x}=3y-y^{’}\\ \\ \Rightarrow be^{-2x}=\frac{3y-y^{’}}{5}\)Substituting the values of \(ae^{3x}\: and\: be^{-2x}\) in equation(3), we get:
\(y^{’’}=9\cdot \frac{(2y+y^{’})}{5}+4\cdot \frac{(3y-y^{’})}{5}\\ \\ \Rightarrow y^{’’}=\frac{18y+9y^{’}}{5}+\frac{12y-4y^{’}}{5}\\ \\ \Rightarrow y^{’’}=\frac{30y+5y^{’}}{5}\\ \\ \Rightarrow y^{’’}=6y+y^{’}\\ \\ \Rightarrow y^{’’}-y^{’}-6y=0\)This is the required differential equation of the given curve.
Q.4: \(y=e^{2x}(a+bx)\)
Solution: Based on the formula given under DIFFERENTIAL EQUATIONS
\(y=e^{2x}(a+bx)\) …..(1)
Differentiate both the sides w.r.t x, we get:
\(y^{’}=2e^{2x}(a+bx)+e^{2x}.b\\ \\ \Rightarrow y^{’}=e^{2x}(2a+2bx+b)\)…………(2)
Multiply equation (1) with 2 and then add it to equation (2), we get:
\(y^{’}-2y=e^{2x}(2a+2bx+b)-e^{2x}(2a+2bx)\\ \\ \Rightarrow y^{’}-2=be^{2x}\) ……(3)
Differentiate both the sides w.r.t x, we get:
\(y^{’’}k-2y^{’}=2be^{2x}\, \, \, \, \, \, \, \, \, \, …….(4)\)Dividing equation (4) by equation (3), we get:
\(\frac{y^{’’}-2y^{’}}{y^{’}-2y}=2\\ \\ \Rightarrow y^{’’}-2y^{’}=2y^{’}-4y\\ \\ \Rightarrow y^{’’}-4y^{’}+4y=0\)This is the required differential equation of the given curve.
Q.5: \(y=e^{x}(a\cos x+b\sin x)\)
Solution: Based on the formula given under DIFFERENTIAL EQUATIONS
\(y=e^{x}(a\cos x+b\sin x)\) . . . . . . . . . . . . (1)
Differentiate both the sides w.r.t x, we get:
\(y^{’}=e^{x}(a\cos x+b\sin x)+e^{x}(-a\sin x+b\cos x)\\ \\ \Rightarrow y^{’}=e^{x}[(a+b)\cos x-(a-b)\sin x]\: \: \: \: \: …………(2)\)Again, Differentiate both the sides w.r.t x, we get:
\(\Rightarrow y^{’’}=e^{x}[(a+b)\cos x-(a-b)\sin x]+e^{x}[-(a+b)\sin x-(a-b)\cos x]\\ \\ y^{’’}=e^{x}[2b\cos x-2a\sin x]\\ \\ y^{’’}=2e^{x}[b\cos x-a\sin x]\\ \\ \Rightarrow \frac{y^{’’}}{2}=e^{x}[b\cos x-a\sin x]\: \: \: \: \: \: \: ………..(3)\)Adding equations (1) and (3), we get:
\(y+\frac{y^{’’}}{2}=e^{x}[(a+b)\cos x-(a-b)\sin x]\\ \\ \Rightarrow y+\frac{y^{’’}}{2}=y^{‘} \\ \\ \Rightarrow 2y+y^{’’}=2y^{’}\\ \\ \Rightarrow y^{’’}-2y^{’}+2y=0\)This is the required differential equation of the given curve.
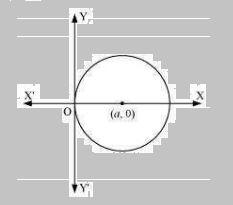
Q.6: Form the differential equation of the family of circles touching the y-axis at the origin.
Solution: Based on the formula given under DIFFERENTIAL EQUATIONS
The centre of the circle touching the y-axis at origin lies on the x-axis.
Let (a, 0) be the centre of the circle.
Since it touches the y-axis at origin, its radius is a.
Now, the equation of the circle with centre (a, 0) and radius (a) is
(x – a)2 + y2 = a2
i.e. x2 + y2 = 2ax . . . . . . . . . . . . . . . (1)
Differentiating equation (1) with respect to x, we get:
2x + 2yy’ = 2a
i.e. x + yy’ = a
Now, on substituting the value of a in equation (1), we get:
\(x^{2}+y^{2}=2(x+yy^{’})x\\ \\ \Rightarrow x^{2}+y^{2}=2x^{2}+2xyy^{’}\\ \\ \Rightarrow 2xyy^{’}+x^{2}=y^{2}\)This is the required differential equation.
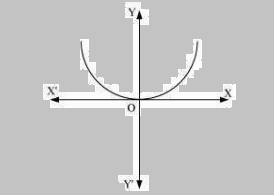
Q.7. Form the differential equation of the family of parabolas having vertex at origin and axis along positive y-axis.
Solution: Based on the formula given under DIFFERENTIAL EQUATIONS
The equation of the parabola having the vertex at origin and the axis along the positive y-axis is:
x2 = 4ay . . . . . . . . . . .(1)
Differentiate both the sides w.r.t x, we get:
2x = 4ay’ . . . . . . . . . . . . . . . . (2)
Dividing equation (2) by equation (1), we get:
\(\frac{2x}{x^{2}}=\frac{4ay^{’}}{4ay}\\ \\ \Rightarrow \frac{2}{x}=\frac{y^{’}}{y}\\ \\ \Rightarrow xy^{’}=2y\\ \\ \Rightarrow xy^{’}-2y=0\)This is the required differential equation.
Q.8: Form the differential equation of the family of ellipses having foci on y-axis and centre at origin.
Solution:
The equation of the family of ellipses having foci on the y-axis and the centre at origin is as follows:
\(\frac{x^{2}}{b^{2}}+\frac{y^{2}}{a^{2}}=1\: \: \: \: \: \: \: \: \: \: …..(1)\)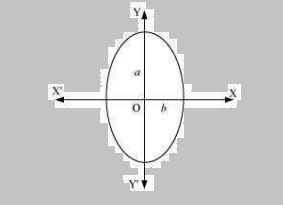
Differentiate both the sides w.r.t x, we get:
\(\frac{2x}{b^{2}}+\frac{2yy^{‘}}{b^{2}}=0\\ \\ \Rightarrow \frac{x}{b^{2}}+\frac{yy^{‘}}{a^{2}}=0\: \: \: \: \: \: \: \: (2)\)Again, differentiate both the sides w.r.t x, we get:
\(\frac{1}{b^{2}}+\frac{y^{’}\cdot y^{’}+y.y^{’’}}{a^{2}}=0\\ \\ \Rightarrow \frac{1}{b^{2}}+\frac{1}{a^{2}}(y^{‘2}+yy^{’’})=0\\ \\ \Rightarrow \frac{1}{b^{2}}=-\frac{1}{a^{2}}(y^{’2}+yy^{’’})\)Substituting this value in equation (2), we get:
\(x[-\frac{1}{a^{2}}((y^{’2})+yy^{’})]+\frac{yy^{’}}{a^{2}}=0\\ \\ \Rightarrow -x(y^{’})^{2}-xyy^{’’}+yy^{’}=0\\ \\ \Rightarrow xyy^{’’}+x(y^{‘})^{2}-yy^{’}=0\)This is the required differential equation.
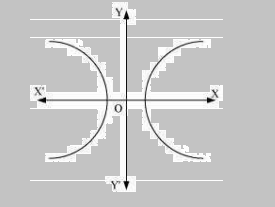
Q.9: Form the differential equation of the family of hyperbolas having foci on x-axis and centre at origin.
Solution: Based on the formula given under DIFFERENTIAL EQUATIONS
The equation of the family of hyperbolas with the centre at origin and foci along the x-axis is:
\(\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}=1\) …………(1)
Differentiate both the sides w.r.t x, we get:
\(\frac{2x}{a^{2}}-\frac{2yy^{’}}{b^{2}}=0\\ \\ \Rightarrow \frac{x}{a^{2}}-\frac{yy^{’}}{b^{2}}=0\) ……….. (2)
Again, differentiate both the sides w.r.t x, we get:
\(\frac{1}{a^{2}}-\frac{y^{’}\cdot y^{’}+yy^{’’}}{b^{2}}=0\\ \\ \Rightarrow \frac{1}{a^{2}}=\frac{1}{b^{2}}((y^{’})^{2}+yy^{’’})\)Substituting the value of \(\frac{1}{a^{2}}\) in equation (2):
\(\frac{x}{b^{2}}((y^{’})^{2}+yy^{’’})-\frac{yy^{’}}{b^{2}}=0\\ \\ x(y^{’})^{2}+xyy^{’’}-yy^{’}=0\\ \\ \Rightarrow xyy^{’’}+x(y^{’})^{2}-yy^{’}=0\)This is the required differential equation.
Q.10: Form the differential equation of the family of circles having centre on y-axis and radius 3 units.
Solution: Based on the formula given under DIFFERENTIAL EQUATIONS
Let the center of the circle on y-axis be (0, b).
The differential equation of the family of circles with centre at (0, b) and radius 3 is as follows:
\(x^{2}+(y-b)^{2}=3^{2}\\ \\ \Rightarrow x^{2}+(y-b)^{2}=9\: \: \: \: \: …(1)\)Differentiate equation (1) with respect to x, we get:
\(2x+2(y-b)\cdot y^{’}=0\\ \\ \Rightarrow (y-b)\cdot y^{’}=-x\\ \\ \Rightarrow y-b=\frac{-x}{y^{’}}\)Substitute the value of (y – b) in equation (1), we get:
\(x^{2}+(\frac{-x}{y^{’}})^{2}=9\\ \\ \Rightarrow x^{2}[1+\frac{1}{(y^{’})^{2}}]=9\\ \\ \Rightarrow x^{2}((y^{‘})^{2}+1)=9(y^{’})^{2}\\ \\ \Rightarrow (x^{2}-9)(y^{’})^{2}+x^{2}=0\)This is the required differential equation.
Q.11.Which of the following differential equations has \(y=c_{1}e^{x}+c_{2}e^{-x}\) as the general solution?
(i) \(\frac{d^{2}y}{dx^{2}}+y=0\)
(ii) \(\frac{d^{2}y}{dx^{2}}-y=0\)
(iii) \(\frac{d^{2}y}{dx^{2}}+1=0\)
(iv) \(\frac{d^{2}y}{dx^{2}}-1=0\)
Solution: Based on the formula given under DIFFERENTIAL EQUATIONS
The given equation is:
\(y=c_{1}e^{x}+c_{2}e^{-x}\) . . . . . . . . . . . . . . . (1)
Differentiate equation (1) with respect to x, we get:
\(\frac{dy}{dx}=c_{1}e^{x}-c_{2}e^{-x}\)Again, differentiate with respect to x, we get:
\(\frac{d^{2}y}{dx^{2}}=c_{1}e^{x}-c_{2}e^{-x}\\ \\ \Rightarrow \frac{d^{2}y}{dx^{2}}=y\\ \\ \Rightarrow \frac{d^{2}y}{dx^{2}}-y=0\)This is the required differential equation of the given equation of curve.
Hence, the correct answer is (ii).
Q.12: Which of the following differential equation has y = x as one of its particular solution?
(i) \(\frac{d^{2}y}{dx^{2}}-x^{2}\frac{dy}{dx}+xy=x\)
(ii) \(\frac{d^{2}y}{dx^{2}}+x\frac{dy}{dx}+xy=x\)
(iii) \(\frac{d^{2}y}{dx^{2}}-x^{2}\frac{dy}{dx}+xy=0\)
(iv) \(\frac{d^{2}y}{dx^{2}}+x\frac{dy}{dx}+xy=0\)
Solution: Based on the formula given under DIFFERENTIAL EQUATIONS
The given equation of curve is y = x.
Differentiate with respect to x, we get:
\(\frac{dy}{dx}=1\: \: \: \: \: ….(1)\)Again, differentiate with respect to x, we get:
\(\frac{d^{2}y}{dx^{2}}=0\: \: \: \: \: ….(2)\)Now, on substituting the values of y:
\(\frac{d^{2}y}{dx^{2}}\), and \(\frac{dy}{dx}\) from equation (1) and (2) in each of the given alternatives, we find that only the differential equation given in alternative C is correct.
\(\frac{d^{2}y}{dx^{2}}-x^{2}\frac{dy}{dx}+xy=0-x^{2}\cdot 1+x\cdot x=-x^{2}+x^{2}=0\)Hence, the correct answer is (iii).
Exercise-9.4
Q.1: \(\frac{dy}{dx}=\frac{1-\cos x}{1+\cos x}\)
Solution: Based on the formula given under DIFFERENTIAL EQUATIONS
The given differential equation is:
\(\frac{dy}{dx}=\frac{1-\cos x}{1+\cos x}\) \(\frac{dy}{dx}=\frac{1-\cos x}{1+\cos x}\\ \\ \Rightarrow \frac{dy}{dx}=\frac{2\sin ^{2}\frac{x}{2}}{2\cos ^{2}\frac{x}{2}}=\tan ^{2}\frac{x}{2}\\ \\ \Rightarrow \frac{dy}{dx}=(\sec ^{2}\frac{x}{2}-1)\)Separate the variables, we get:
\({dy}=(\sec ^{2}\frac{x}{2}-1)dx\)Now, integrating both sides of this equation, we get:
\(\int {dy}=\int (\sec ^{2}\frac{x}{2}-1)dx=\int \sec ^{2}\frac{x}{2}dx-\int dx\\ \\ \Rightarrow y=2\tan \frac{x}{2}-x+C\)This is the required general solution of the given differential equation.
Q.2: \(\frac{dy}{dx}=\sqrt{4-y^{2}}\: (-2<y<2)\)
Solution: Based on the formula given under DIFFERENTIAL EQUATIONS
The given differential equation is:
\(\frac{dy}{dx}=\sqrt{4-y^{2}}\)Separate the variables, we get:
\(\Rightarrow \frac{dy}{\sqrt{4-y^{2}}}=dx\)Now, integrating both sides of this equation, we get:
\(\int \frac{dy}{\sqrt{4-y^{2}}}=\int dx\\ \\ \Rightarrow \sin ^{-1}\frac{y}{2}=x+C\\ \\ \Rightarrow \frac{y}{2}=\sin (x+C)\\ \\ \Rightarrow y=2\sin (x+C)\)This is the required general solution of the given differential equation.
Q.3: \(\frac{dy}{dx}+y=1\: (y\neq 1)\)
Solution: Based on the formula given under DIFFERENTIAL EQUATIONS
The given differential equation is:
\(\frac{dy}{dx}+y=1\\ \\ \Rightarrow dy+y\: dx=dx\\ \\ \Rightarrow dy=(1-y)dx\)Separate the variables, we get:
\(\Rightarrow\frac{ dy}{1-y}=dx\)Now, integrating both sides, we get:
\(\int \frac{ dy}{1-y}=\int dx\\ \\ \Rightarrow log(1-y)=x+log\, C\\ \\ \Rightarrow -log\,C-log(1-y)=x\\ \\ \Rightarrow log\,C(1-y)=e^{-x}\\ \\ \Rightarrow 1-y=\frac{1}{C}e^{-x}\\ \\ \Rightarrow y=1-\frac{1}{C}e^{-x}\\ \\ \Rightarrow y=1+Ae^{-x}\: (where\: A=-\frac{1}{C})\)This is the required general solution of the given differential equation.
Q.4: \(\sec ^{2}x\tan\: y \: dx+\sec ^{2}\: y\, \tan \: x\, dy=0\)
Solution: Based on the formula given under DIFFERENTIAL EQUATIONS
The given differential equation is:
\(\sec ^{2}x\tan\: y \: dx+\sec ^{2}\: y\, \tan \: x\, dy=0\\ \\ \Rightarrow \frac{\sec ^{2}x\tan\: y \: dx+\sec ^{2}\: y\, \tan \: x\, dy}{\tan \, x\, \tan \, y}=0\\ \\ \Rightarrow \frac{\sec ^{2}x}{\tan x}dx+\frac{\sec ^{2}y}{\tan y}dy=0\\ \\ \Rightarrow \frac{\sec ^{2}x}{\tan x}dx=-\frac{\sec ^{2}y}{\tan y}dy\)Integrating both sides of this equation, we get:
\(\int \frac{\sec ^{2}x}{\tan x}dx=-\int \frac{\sec ^{2}y}{\tan y}dy\) . . . . . . . . . . . . (1)
Let, tan x = t
Therefore, \(\frac{d}{dx}(\tan x)= \frac{dt}{dx}\\ \\ \Rightarrow \sec ^{2}x=\frac{dt}{dx}\\ \\ \Rightarrow \sec ^{2}xdx=dt\)
Now,
\(\int \frac{\sec ^{2}x}{\tan x}dx=\int \frac{1}{t}dt\;=\;log\, t\;=\;log(\tan x)\\\)Similarly, \(\int \frac{\sec ^{2}x}{\tan x}dx=log(\tan y)\)
Substituting these values in equation (1), we get:
\(log(\tan x)=-log(\tan y)+log\, C\\ \\ \Rightarrow log(\tan x)=log(\frac{C}{\tan y})\\ \\ \Rightarrow \tan x=\frac{C}{\tan y}\\ \\ \Rightarrow \tan x\, \tan y=C\)This is the required general solution of the given differential equation.
Q.5: \((e^{x}+e^{-x})dy-(e^{x}-e^{-x})dx=0\)
Solution: Based on the formula given under DIFFERENTIAL EQUATIONS
The given differential equation is:
\((e^{x}+e^{-x})dy-(e^{x}-e^{-x})dx=0\\ \\ \Rightarrow (e^{x}+e^{-x})dy=(e^{x}-e^{-x})dx\\ \\ \Rightarrow dy=[\frac{e^{x}-e^{-x}}{e^{x}+e^{-x}}]dx\)Integrating both sides of this equation, we get:
\(\int dy=\int [\frac{e^{x}-e^{-x}}{e^{x}+e^{-x}}]dx+C\\ \\ \Rightarrow y=\int [\frac{e^{x}-e^{-x}}{e^{x}+e^{-x}}]dx+C\: \: \: \: \: ….(1)\)Let \((e^{x}+e^{-x})\)
\(\frac{d}{dx}(e^{x}+e^{-x})=\frac{dt}{dx}\\ \\ \Rightarrow e^{x}-e^{-x}=\frac{dt}{dx}\\ \\ \Rightarrow (e^{x}-e^{-x})dx=dt\)Substituting this value in equation (1), we get:
\(y=\int \frac{1}{t}dt+C\\ \\ \Rightarrow y=log(t)+C\\ \\ \Rightarrow y=log(e^{x}+e^{-x})+C\)This is the required general solution of the given differential equation.
Q.6: \(\frac{dy}{dx}=(1+x^{2})(1+y^{2})\)
Solution: Based on the formula given under DIFFERENTIAL EQUATIONS
The given differential equation is:
\(\frac{dy}{dx}=(1+x^{2})(1+y^{2})\\ \\ \Rightarrow \frac{dy}{1+y^{2}}=(1+x^{2})dx\)Integrating both sides of this equation, we get:
\(\int \frac{dy}{1+y^{2}}=\int (1+x^{2})dx\\ \\ \Rightarrow \tan ^{-1}y=\int dx+\int x^{2}dx\\ \\ \Rightarrow \tan ^{-1}y=x+\frac{x^{3}}{3}+C\)This is the required general solution of the given differential equation.
Q.7: \(y\, log\, y\, dx-x\, dy=0\)
Solution:
The given differential equation is:
\(y\, log\, y\, dx-x\, dy=0\\ \\ \Rightarrow y\, log\, y\, dx=x\, dy\\ \\ \Rightarrow \frac{dy}{y\, log\, y}=\frac{dx}{x}\)Integrating both sides, we get:
\(\int \frac{dy}{y\, log\, y}=\int \frac{dx}{x}\) . . . . . . . . . . . . . . (1)
Let, log y = t
Therefore, \(\frac{d}{dy}(log\, y)=\frac{dt}{dy}\\ \\ \Rightarrow \frac{1}{y}=\frac{dt}{dy}\\ \\ \Rightarrow \frac{1}{y}dy=dt\)
Substituting this value in equation (1), we get:
\(\int \frac{dt}{t}=\int \frac{dx}{x}\\ \\ \Rightarrow log \, t=log\, x+log \, C\\ \\ \Rightarrow log(log\, y)=log\, Cx\\ \\ \Rightarrow log\, y=Cx\\ \\ \Rightarrow y=e^{Cx}\)This is the required general solution of the given differential equation.
Q.8: \(x^{5}\frac{dy}{dx}=-y^{5}\)
Solution: Based on the formula given under DIFFERENTIAL EQUATIONS
The given differential equation is:
\(x^{5}\frac{dy}{dx}=-y^{5}\\ \\ \Rightarrow \frac{dy}{y^{5}}=-\frac{dx}{x^{5}}\\ \\ \Rightarrow \frac{dx}{x^{5}}+\frac{dy}{y^{5}}=0\)Integrating both sides, we get:
\(\int \frac{dx}{x^{5}}+\int \frac{dy}{y^{5}}=k\) (where k is any constant)
\(\int {x^{-5}}dx+\int {y^{-5}dy}=k\\ \\ \Rightarrow \frac{x^{-4}}{-4}+\frac{y^{-4}}{-4}=k\\ \\ \Rightarrow x^{-4}+y^{-4}=-4k\\ \\ \Rightarrow x^{-4}+y^{-4}=C\) (C=-4k)
This is the required general solution of the given differential equation.
Q.9. \(\frac{dy}{dx}=\sin ^{-1}x\)
Solution: Based on the formula given under DIFFERENTIAL EQUATIONS
The given differential equation is:
\(\frac{dy}{dx}=\sin ^{-1}x\\ \\ \Rightarrow dy=\sin ^{-1}x\, dx\)Integrating both sides, we get:
\(\int dy=\int \sin ^{-1}x\, dx\\ \\ \Rightarrow y=\int (\sin ^{-1}x-1)dx\\ \\ \Rightarrow y=\sin ^{-1}x\cdot \int (1)dx-\int [(\frac{d}{dx}(\sin ^{-1}x)\cdot \int (1)dx)]dx\\ \\ \Rightarrow y=\sin ^{-1}x\cdot x-\int (\frac{1}{\sqrt{1-x^{2}}}\cdot x)dx\\ \\ \Rightarrow y=x\sin ^{-1}x+\int \frac{-x}{\sqrt{1-x^{2}}}dx\: \: \: \: \: ….(1)\)Let, \(1-x^{2}=t\\ \\ \Rightarrow \frac{d}{dx}(1-x^{2})=\frac{dt}{dx}\\ \\ \Rightarrow -2x=\frac{dt}{dx}\\ \\ \Rightarrow x\, dx=-\frac{1}{2}dt\)
Substituting this value in equation (1), we get:
\(y=x\sin ^{-1}x+\int \frac{1}{2\sqrt{t}}dt\\ \\ \Rightarrow y=x\sin ^{-1}x+\frac{1}{2}\cdot \int (t)^{-\frac{1}{2}}dt\\ \\ \Rightarrow y=x\sin ^{-1}x+\frac{1}{2}\cdot \frac{t^{\frac{1}{2}}}{\frac{1}{2}}+C\\ \\ \Rightarrow y=x\sin ^{-1}x+\sqrt{t}+C\\ \\ \Rightarrow y=x\sin ^{-1}x+\sqrt{1-x^{2}}+C\)This is the required general solution of the given differential equation.
Q.10. \(e^{x}\tan y\, dx+(1-e^{x})\sec ^{2}y\, dy=0\)
Solution: Based on the formula given under DIFFERENTIAL EQUATIONS
\(e^{x}\tan y\, dx+(1-e^{x})\sec ^{2}y\, dy=0\\ \\ (1-e^{x})\sec ^{2}y\, dy=-e^{x}\tan y\, dx\)Separating the variables, we get:
\(\frac{\sec ^{2}y}{\tan y}dy=\frac{-e^{x}}{1-e^{x}}dx\)Integrating both sides, we get:
\(\int \frac{\sec ^{2}y}{\tan y}dy=\int \frac{-e^{x}}{1-e^{x}}dx\: \: \: \: \: ….(1)\)Let, tan y = u
\(\frac{d}{dy}{\tan y}=\frac{du}{dy}\\ \\ \Rightarrow \sec ^{2}y=\frac{du}{dy}\\ \\ \Rightarrow \sec ^{2}ydy=du\)Therefore, \(\\\int \frac{\sec ^{2}y}{\tan y}dy=\int \frac{du}{u}=log\, u=log(\tan y)\)
Now, let 1 – ex = t
Therefore, \(\frac{d}{dx}(1-e^{x})=\frac{dt}{dx}\\ \\ \Rightarrow -e^{x}=\frac{dt}{dx}\\ \\ \Rightarrow -e^{x}dx=dt\\ \\ \Rightarrow \int \frac{-e^{x}}{1-e^{x}}dx=\int \frac{dt}{t}=log\:t=log(1-e^{x})\)
Substituting the values of \(\int \frac{\sec ^{2}y}{\tan y}dy\) and \(\int \frac{-e^{x}}{1-e^{x}}dx\)
\(\Rightarrow log(\tan y)=log(1-e^{x})+log\, C\\ \\ \Rightarrow log(\tan y)=log[C(1-e^{x})]\\ \\ \Rightarrow \tan y=C(1-e^{x})\)This is the required general solution of the given differential equation.
Exercise-9.5
Q.1: (x2 + xy)dy = (x2 + y2)dx
Ans: Based on the formula given under DIFFERENTIAL EQUATIONS
Given:
(x2 + xy)dy = (x2 + y2)dx
\(\frac{dy}{dx}=\frac{x^{2}+y^{2}}{x^{2}+xy}\) . . . . . . . . . . . (1)
Let, F(x, y) = \(\frac{x^{2}+y^{2}}{x^{2}+xy}\)
Now,
F(λx, λy) = \(\frac{(\lambda x)^{2}+(\lambda y)^{2}}{(\lambda x)^{2}+(\lambda x )(\lambda y)}=\frac{x^{2}+y^{2}}{x^{2}+xy}=\lambda ^{0}\cdot F(x,y)\)
Here we have observed that equation (1) is a homogeneous equation.
Let, y = vx
Differentiate both the sides w.r.t. x, we get:
\(\frac{dy}{dx}=v+x\frac{dv}{dx}\)Substitute the values of v and \(\frac{dy}{dx}\) in equation(1), we get:
\(\boldsymbol{\Rightarrow }\) \(v+x\frac{dv}{dx}=\frac{x^{2}+(vx)^{2}}{x^{2}+x(vx)}\\ \\ \Rightarrow v+x\frac{dv}{dx}=\frac{1+v^{2}}{1+v}\\ \\ \Rightarrow x\frac{dv}{dx}=\frac{1+v^{2}}{1+v}-v=\frac{(1+v^{2})-v(1+v)}{1+v}\\ \\ \Rightarrow x\frac{dv}{dx}=\frac{1-v}{1+v}\\ \\ \Rightarrow (\frac{1+v}{1-v})=dv=\frac{dx}{x}\\ \\ \Rightarrow (\frac{2-1+v}{1-v})dv=\frac{dx}{x}\\ \\ \Rightarrow (\frac{2}{1-v}-1)dv=\frac{dx}{x}\)
Integrate on both the sides, we get:
\(\boldsymbol{\Rightarrow }\) -2log(1-v)-v=log x – log k
\(\Rightarrow v=-2log(1-v)-log x+log k\\ \\ \Rightarrow v=log[\frac{k}{x(1-v)^{2}}]\\ \\ \Rightarrow \frac{y}{x}=log[\frac{k}{x(1-\frac{y}{x})^{2}}]\\ \\ \Rightarrow \frac{y}{x}=log[\frac{kx}{(x-y)^{2}}]\\ \\ \Rightarrow \frac{kx}{(x-y)^{2}}=e^{\frac{y}{x}}\\ \\ \Rightarrow (x-y)^{2}=k\;x\;e^{-\frac{y}{x}}\\\)This is the required solution of the given differential equation.
Q.2: y = \(\frac{x+y}{x}\)
Ans: Based on the formula given under DIFFERENTIAL EQUATIONS
Given:
y = \(\frac{x+y}{x}\)
\(\Rightarrow \frac{dy}{dx}=\frac{x+y}{x}\) . . . . . . . . . . (1)
Let F(x,y)= \(\frac{x+y}{x}\)
Now, F(λx,λy)= \(\frac{\lambda x+\lambda y}{\lambda x}=\frac{x+y}{x}=\lambda ^{0}F(x,y)\)
Here we have observed that equation (1) is a homogeneous equation.
Let, y = vx
Differentiate both the sides w.r.t. x, we get
\(\frac{dy}{dx}=v+x\frac{dv}{dx}\)Substitute the values of v and \(\frac{dy}{dx}\) in equation(1), we get:
\(\boldsymbol{\Rightarrow }\) \(v+x\frac{dv}{dx}=\frac{x+vx}{x}\\ \\ \Rightarrow v+x\frac{dv}{dx}=1+v\\ \\ \Rightarrow x\frac{dv}{dx}=1\\ \\ \Rightarrow dv=\frac{dx}{x}\)
Integrate on both the sides, we get:
V = log x + C
\(\Rightarrow \frac{y}{x}=logx+c\\ \\ \Rightarrow y=xlogx+Cx\)This is the required solution of the given differential equation.
Q.3: (x-y)dy-(x+y)dx=0
Ans: Based on the formula given under DIFFERENTIAL EQUATIONS
Given:
(x – y)dy – (x + y)dx = 0
\(\Rightarrow \frac{dy}{dx}=\frac{x+y}{x-y}\) . . . . . . . . . . (1)
Let, F(x, y) = \(\frac{x+y}{x-y}\)
Therefore, \(F(\lambda x,\lambda y)=\frac{\lambda x+\lambda y}{\lambda x-\lambda y}=\frac{x+y}{x-y}=\lambda ^{0}\cdot F(x,y)\)
Here we have observed that equation (1) is a homogeneous equation.
Let, y = vx
Differentiate both the sides w.r.t. x, we get:
\(\frac{dy}{dx}=v+x\frac{dv}{dx}\)Substitute the values of v and \(\frac{dy}{dx}\) in equation(1), we get:
\(\boldsymbol{\Rightarrow }\) \(v+x\frac{dv}{dx}=\frac{x+vx}{x-vx}=\frac{1+v}{1-v}\\ \\ x\frac{dv}{dx}=\frac{1+v}{1-v}-v=\frac{1+v-v(1-v)}{1-v}\\ \\ \Rightarrow x\frac{dv}{dx}=\frac{1+v^{2}}{1-v}\\ \\ \Rightarrow \frac{1-v}{(1+v^{2})}dv=\frac{dx}{x}\\ \\ \Rightarrow (\frac{1}{1+v^{2}}-\frac{v}{1-v^{2}})dv=\frac{dx}{x}\\\)
Integrate on both the sides, we get:
\(\boldsymbol{\Rightarrow }\) \(tan^{-1}v-\frac{1}{2}log(1+v^{2})=log\, x+C\\ \\ \Rightarrow tan^{-1}(\frac{y}{x})-\frac{1}{2}log[1+(\frac{y}{x})^{2}]=log\, x+C\\ \\ \Rightarrow tan^{-1}(\frac{y}{x})-\frac{1}{2}log(\frac{x^{2}+y^{2}}{x^{2}})=log\, x+C\\ \\ \Rightarrow tan^{-1}(\frac{y}{x})-\frac{1}{2}[log(x^{2}+y^{2})-log\, x^{2}]=log\, x+C\\ \\ \Rightarrow tan^{-1}(\frac{y}{x})=\frac{1}{2}log(x^{2}+y^{2})+C\\\)
This is the required solution of the given differential equation.
Q.4: (x2 – y2) dx + 2xy dy = 0
Ans: Based on the formula given under DIFFERENTIAL EQUATIONS
Given,
(x2 – y2)dx + 2xy dy = 0
\(\Rightarrow \frac{dy}{dx}=\frac{-(x^{2}-y^{2})}{2xy}\) . . . . . . . . . (1)
Let, F(x, y) = \(\frac{-(x^{2}-y^{2})}{2xy}\)
Therefore, \(F(\lambda x,\lambda y)=[\frac{(\lambda x)^{2}-(\lambda y)^{2}}{2xy}]=\frac{-(x^{2}-y^{2})}{2(\lambda x)(\lambda y)}=\frac{-(x^{2}-y^{2})}{2xy}=\lambda^{\circ}\cdot F(x,y)\)
Here we have observed that equation (1) is a homogeneous equation.
Let, y = vx
Differentiate both the sides w.r.t. x, we get:
\(\frac{dy}{dx}=v+x\frac{dv}{dx}\)Substitute the values of v and \(\frac{dy}{dx}\) in equation(1), we get:
\(\boldsymbol{\Rightarrow }\) \(v+x\frac{dv}{dx}=-[\frac{x^{2}-(vx)^{2}}{2x\cdot (vx)}]=\frac{v^{2}-1}{2v}\\ \\ \Rightarrow x\frac{dv}{dx}=\frac{v^{2}-1}{2v}-v=\frac{v^{2}-1-2v^{2}}{2v}\\ \\ \Rightarrow x\frac{dv}{dx}=-\frac{(1+v^{2})}{2v}\\ \\ \Rightarrow \frac{2v}{1+v^{2}}dv=-\frac{dx}{x}\)
Integrate on both the sides, we get:
\(\boldsymbol{\Rightarrow }\) Log(1 + v2) = -log x + log C = \(log\frac{C}{x}\)
\(\Rightarrow 1+v^{2}=\frac{C}{x}\\ \\ \Rightarrow [1+\frac{y^{2}}{x^{2}}]=\frac{C}{x}\\ \\ \Rightarrow x^{2}+y^{2}=Cx\)This is the required solution of the given differential equation.
Q.5: \(x^{2}\frac{dy}{dx}-x^{2}-2y^{2}+xy\)
Ans: Based on the formula given under DIFFERENTIAL EQUATIONS
Given:
\(x^{2}\frac{dy}{dx}-x^{2}-2y^{2}+xy\)\(\frac{dy}{dx}=\frac{x^{2}-2y^{2}+xy}{x^{2}}\) . . . . . . . . . . . (1)
Let F(x,y)= \(\frac{ x^{2}- 2y^{2} + xy}{ x^{2}}\)
\(F( \lambda x, \lambda y)= \frac{( \lambda x )^{ 2}-2( \lambda y)^{2}+( \lambda x)( \lambda x)}{( \lambda x)^{2}}=\frac{ x^{2} – 2y^{2}+ x y }{ x^{2}}=\lambda ^{\circ}\cdot F( x , y)\)Here we have observed that equation (1) is a homogeneous equation.
Let, y = vx
Differentiate both the sides w.r.t. x, we get:
\(\frac{ dy }{ dx } = v + x \frac { dv }{ dx }\)Substitute the values of v and \(\frac{ dy }{ dx }\) in equation(1), we get:
\(\boldsymbol{\Rightarrow }\) \(v+x\frac{dv}{dx}=\frac{x^{2}-2(vx)^{2}+x\cdot (vx)}{x^{2}}\\ \\ \Rightarrow v+x\frac{dv}{dx}=1-2v^{2}+v\\ \\ \Rightarrow x\frac{dv}{dx}=1-2v^{2}\\ \\ \Rightarrow \frac{dv}{1-2v^{2}}=\frac{dx}{x}\\ \\ \Rightarrow \frac{1}{2}\cdot \frac{dv}{\frac{1}{2}-v^{2}}=\frac{dx}{x}\\ \\ \Rightarrow \frac{1}{2}[\frac{dv}{(\frac{1}{\sqrt{2}})^{2}-v^{2}}]=\frac{dx}{x}\)
Integrate on both the sides, we get:
\(\boldsymbol{\Rightarrow }\) \( \frac {1} {2} \cdot \frac {1} { 2\times \frac{1} {\sqrt {2} }}log\left | \frac{ \frac {1} { \sqrt {2} }+v}{ \frac {1} {\ sqrt {2}}-v} \right |=log\left | x \right |+C\\ \\ \\ \Rightarrow \frac {1} {2\sqrt {2}}log\left | \frac{\frac {1} {\sqrt {2}}+\frac {y}{x}}{\frac {1}{ \sqrt {2}}-\frac {y} {x} } \right |=log\left | x \right |+C\\ \\ \\ \Rightarrow \frac {1} {2\times \frac {1} {\sqrt {2}}}log\left | \frac{x + 2\sqrt {2} y}{x + 2 \sqrt {2} y} \right |=log\left | x \right |+C\)
This is the required solution of the given differential equation.
Q.6: xdy – ydx = \(\sqrt{x^{2}+y^{2}}dx\)
Ans: Based on the formula given under DIFFERENTIAL EQUATIONS
xdy – ydx = \(\sqrt{x^{2}+y^{2}}dx\)
\(\Rightarrow xdy=[y+\sqrt{x^{2}+y^{2}}]dx\\ \\ \Rightarrow \frac{dy}{dx} =\frac{y+\sqrt{x^{2}+y^{2}}}{x^{2}}\) . . . . . . . . . . . . . (1)
Let, F(x,y) = \(\frac{y+\sqrt{x^{2}+y^{2}}}{x^{2}}\)
Therefore, \( F(\lambda x,\lambda y)=\frac{\lambda x+\sqrt{(\lambda x)^{2}(\lambda y)^{2}}}{x}=\lambda ^{0}\cdot F(x,y)\)
Here we have observed that equation (1) is a homogeneous equation.
Let, y = vx
Differentiate both the sides w.r.t. x, we get:
\(\frac{dy}{dx}=v+x\frac{dv}{dx}\)Substitute the values of v and \(\frac{dy}{dx}\) in equation(1), we get:
\(\boldsymbol{\Rightarrow }\) \(v+x\frac{dv}{dx}=\frac{vx+\sqrt{x^{2}+(vx)^{2}}}{x}\\ \\ \Rightarrow v+x\frac{dv}{dx}=v+\sqrt{1+v^{2}}\\ \\ \Rightarrow \frac{dv}{\sqrt{1+v^{2}}}=\frac{dx}{x}\)
Integrate on both the sides, we get:
\(\boldsymbol{\Rightarrow }\) \(log\left | v+\sqrt{1+v^{2}} \right |=log\left | x \right |+logC\\ \\ \Rightarrow log\left | \frac{y}{x}+\sqrt{1+\frac{y^{2}}{x^{2}}} \right |=log\left | Cx \right |\\ \\ \Rightarrow log\left | \frac{y+\sqrt{x^{2}+y^{2}}}{x} \right |=log\left | Cx \right |\\ \\ \Rightarrow y+\sqrt{x^{2}+y^{2}}=Cx^{2}\)
This is the required solution of the given differential equation.
Q.7: \(\left \{xcos(\frac{y}{x})+ysin(\frac{y}{x})\right \} ydx =\left \{ ysin(\frac{y}{x} ) -xcos(\frac{y}{x})\right \}x\;dy\)
Ans: Based on the formula given under DIFFERENTIAL EQUATIONS
Given:
\(\left \{xcos( \frac {y}{x})+y sin( \frac {y} {x})\right \} y dx =\left \{ ysin( \frac {y}{x} ) -xcos( \frac {y}{x})\right \} xdy\\\)\(\\\frac{dy}{dx}=\frac{\left \{xcos(\frac{y}{x})+ysin(\frac{y}{x})\right \} y }{\left \{ ysin(\frac{y}{x} ) -xcos(\frac{y}{x})\right \}x}\) . . . . . . . . . . (1)
Let, F(x, y) = \(\frac{dy}{dx}=\frac{\left \{xcos(\frac{y}{x})+ysin(\frac{y}{x})\right \} y }{\left \{ ysin(\frac{y}{x} ) -xcos(\frac{y}{x})\right \}x}\)
Therefore, \(F(\lambda x,\lambda y)=\frac{\left \{\lambda xcos(\frac{\lambda y}{\lambda x})+\lambda ysin(\frac{\lambda y}{\lambda x})\right \} \lambda y }{\left \{ \lambda ysin(\frac{\lambda y}{\lambda x} ) -\lambda xcos(\frac{\lambda y}{\lambda x})\right \}\lambda x}\\ \\ =\frac{\left \{xcos(\frac{y}{x})+ysin(\frac{y}{x})\right \} y }{\left \{ ysin(\frac{y}{x} ) -xcos(\frac{y}{x})\right \}x}\\ \\ =\lambda ^{0}\cdot F(x,y)\)
Here we have observed that equation (1) is a homogeneous equation.
Let, y = vx
Differentiate both the sides w.r.t. x, we get:
\(\frac{dy}{dx}=v+x\frac{dv}{dx}\)\(\boldsymbol{\Rightarrow }\) Substitute the values of v and \(\frac{dy}{dx}\) in equation(1), we get:
\(v+x\frac{dv}{dx}=\frac{(x\,cos\,v+vx\,sin\,v)\cdot vx}{(vx\,sin\,v-x\,cos\,v)\cdot x}\\ \\ \Rightarrow v+x\frac{dv}{dx}=\frac{v\,cos\,v+v^{2}\,sin\,v}{v\,sin\,v-cos\,v}\\ \\ \Rightarrow x\frac{dv}{dx}=\frac{v\,cos\,v+v^{2}\,sin\,v}{v\,sin\,v-cos\,v}-v\\ \\ \Rightarrow x\frac{dv}{dx}=\frac{v\,cos\,v+v^{2}\,sin\,v-v^{2}\,sin\,v+v\,cos\,v}{v\,sin\,v-cos\,v}\\ \\ \Rightarrow x\frac{dv}{dx}=\frac{2v\,cos\,v}{v\,sin\,v-cos\,v}\\ \\ \Rightarrow [\frac{v\,sin\,v-cos\,v}{v\,cos\,v}]dv=\frac{2dx}{x}\\ \\ \Rightarrow (tan\,v-\frac{1}{v})dv=\frac{2dx}{x}\)Integrate on both the sides, we get:
\(\boldsymbol{\Rightarrow }\) Log(sec v) – log v = 2 log x + log C
\(\Rightarrow log ( \frac { sec \,v}{ v })=log\,(Cx^{2})\\ \\ \Rightarrow log( \frac{ sec \,v}{v})=Cx^{2}\\ \\ \Rightarrow \sec \,v = Cx^{2}v\\ \\ \Rightarrow sec(\frac{y}{x})= C-x^{2} \cdot \frac{y}{x}\\ \\ \Rightarrow sec(\frac{y}{x})=Cxy\\ \\ \Rightarrow sec(\frac{y}{x})=\frac{1}{Cxy}=\frac{1}{C}\cdot \frac{1}{xy}\\ \\ \Rightarrow xy\,cos(\frac{y}{x})=k\: \: \: \: \: \: \: \: \: \: \: \: (k=)\frac{1}{C}\)This is the required solution of the given differential equation.
Q.8: \(x\frac{dy}{dx}-y+x\,sin(\frac{y}{x})=0\)
Ans: Based on the formula given under DIFFERENTIAL EQUATIONS
\(x\frac{dy}{dx}-y+x\,sin(\frac{y}{x})=0\)\(\Rightarrow x\frac{dy}{dx}=y-xsin(\frac{y}{x})\\ \\ \Rightarrow \frac{dy}{dx}=\frac{y-xsin(\frac{y}{x})}{x}\) . . . . . . . . . (1)
Let, F(x , y) = \(\frac{y-xsin(\frac{y}{x})}{x}\)
Therefore, \(F(\lambda x,\lambda y)=\frac{\lambda y-\lambda xsin(\frac{\lambda y}{\lambda x})}{\lambda x}=\frac{y-xsin(\frac{y}{x})}{x}=\lambda ^{0}\cdot F(x,y)\)
Here we have observed that equation (1) is a homogeneous equation.
Let, y = vx
Differentiate both the sides w.r.t. x, we get:
\(\frac{dy}{dx}=v+x\frac{dv}{dx}\)Substitute the values of v and \(\frac{dy}{dx}\) in equation(1), we get:
\(\boldsymbol{\Rightarrow }\) \(v+x\frac{dv}{dx}=\frac{vx-x\,sin\,v}{x}\\ \\ \Rightarrow v+x\frac{dv}{dx}=v-sin\, v\\ \\ \Rightarrow -\frac{dv}{sin\, v}=-\frac{dx}{x}\\ \\ \Rightarrow cosec\,v\,dv=-\frac{dx}{x}\\\)
Integrate on both the sides:
\(\boldsymbol{\Rightarrow }\) \(log\left |cosec v – cot v \right |=-logx+log C=log\frac{C}{x}\\ \\ \Rightarrow cosec(\frac{y}{x})-cot(\frac{y}{x})=\frac{C}{x}\\ \\ \Rightarrow \frac{1}{sin(\frac{y}{x})}-\frac{cos(\frac{y}{x})}{sin(\frac{y}{x})}=\frac{C}{x}\\ \\ \Rightarrow x[1-cos(\frac{y}{x})]=Csin(\frac{y}{x})\\\)
This is the required solution of the given differential equation.
Q.9: y dx + x log (\(\frac{y}{x}\)) dy – 2x dy = 0
Ans: Based on the formula given under DIFFERENTIAL EQUATIONS
\(ydx + xlog(\frac{y}{x})dy-2xdy=0\\ \\ \Rightarrow ydx =[2x-xlog(\frac{y}{x})]dy\\ \\ \Rightarrow \frac{dy}{dx}=\frac{y}{2x-xlog(\frac{y}{x})}\) . . . . . . . . . (1)
Let, F(x, y) = \(\frac{y}{2x-xlog(\frac{y}{x})}\)
Therefore, \(F(\lambda x,\lambda y)=\frac{\lambda y}{2\lambda x-\lambda xlog(\frac{\lambda y}{\lambda x})}=\lambda ^{0}\cdot F(x,y)\)
Here we have observed that equation (1) is a homogeneous equation.
Let y = vx
Differentiate both the sides w.r.t. x, we get:
\(\frac{dy}{dx}=v+x\frac{dv}{dx}\\\)Substitute the values of v and \(\frac{dy}{dx}\) in equation(1), we get:
\(\boldsymbol{\Rightarrow }\) \(v+x\frac{dv}{dx}=\frac{vx}{2x-xlogv}\\ \\ \Rightarrow v+x\frac{dv}{dx}=\frac{v}{2-logv}\\ \\ \Rightarrow x\frac{dv}{dx}=\frac{v}{2-logv}-v\\ \\ \Rightarrow x\frac{dv}{dx}=\frac{v-2v+vlogv}{2-logv}\\ \\ \Rightarrow x\frac{dv}{dx}=\frac{vlogv-v}{2-logv}\\ \\ \Rightarrow \frac{2-logv}{vlogv-v}dv=\frac{dx}{x}\\ \\ \Rightarrow [\frac{1+(1-logv)}{v(logv-1)}]dv=\frac{dx}{x}\\ \\ \Rightarrow [\frac{1}{v(logv-1)}-\frac{1}{v}]dv=\frac{dx}{x}\\\)
Integrate on both the sides:
\(\int \frac{1}{v(logv-1)}dv-\int \frac{1}{v}dv=\int \frac{1}{x}dx\\ \\ \Rightarrow \int \frac{1}{v(logv-1)}dv-log v =logx+logC\) . . . . . . . . . . . . (2)
Let, log v – 1 =t
\(\Rightarrow \frac{d}{dv}(log v-1)=\frac{dt}{dv}\\ \\ \Rightarrow \frac{1}{v}=\frac{dt}{dv}\\ \\ \Rightarrow \frac{dv}{v}=dt\)So, equation (1) will become:
\(\int \frac{dt}{t}-logv=logx+logC\\ \\ \Rightarrow log t-log(\frac{y}{x})=log(Cx)\\ \\ \Rightarrow log[log(\frac{y}{x})-1]-log(\frac{y}{x})=log(Cx)\\ \\ \Rightarrow log[\frac{log(\frac{y}{x})-1}{ \frac{y}{x}}]=log(Cx)\\ \\ \Rightarrow \frac{x}{y}[log(\frac{y}{x})-1]=Cx\\ \\ \Rightarrow log(\frac{y}{x})-1=Cy\)This is the required solution of the given differential equation.
Q.10: \((1+e^{\frac{x}{y}})dx+e^{\frac{x}{y}}(1-\frac{x}{y})dy=0\)
Ans: Based on the formula given under DIFFERENTIAL EQUATIONS
\(\boldsymbol{\Rightarrow }\) \((1+e^{\frac{x}{y}})dx+e^{\frac{x}{y}}(1-\frac{x}{y})dy=0\\ \\ \Rightarrow (1+e^{\frac{x}{y}})dx=-e^{\frac{x}{y}}(1-\frac{x}{y})dy\\ \\ \Rightarrow \frac{dx}{dy}=\frac{-e^{\frac{x}{y}}(1-\frac{x}{y})}{1+e^{\frac{x}{y}}}\) . . . . . . . . . . (1)
Let F(x,y) = \(\frac{-e^{\frac{x}{y}}(1-\frac{x}{y})}{1+e^{\frac{x}{y}}}\)
Therefore, \(F(\lambda x,\lambda y)= \frac{-e^{\frac{\lambda x}{\lambda y}}(1-\frac{\lambda x}{\lambda y})}{1+e^{\frac{\lambda x}{\lambda y}}}\\ \\ =\frac{-e^{\frac{x}{y}}(1-\frac{x}{y})}{1+e^{\frac{x}{y}}}\\ \\ =\lambda ^{0}\cdot F(x,y)\)
Here we have observed that equation (1) is a homogeneous equation.
Let, x = vy
\(\frac{d}{dy}(x)=\frac{d}{dy}(vy)\\ \\ \Rightarrow \frac{dx}{dy}=v+y\frac{dv}{dy}\)Differentiate both the sides w.r.t. x, we get
Substitute the values of v and \(\frac{dx}{dy}\) in equation(1), we get as follows:
\(\boldsymbol{\Rightarrow }\) \( v + y \frac {dv}{dx} =\frac{ -e^{v}(1-v)}{1+e}\\ \\ \Rightarrow y\frac{dv}{dy} = \frac{-e^{v} + ve^{v}}{1+e^{v}}-v\\ \\ \Rightarrow y\frac{dv}{dy} = \frac{-e^{v}+ve^{v}-v-ve^{v}}{1 + e^{v}}\\ \\ \Rightarrow y\frac{dv}{dy} = -[\frac{v+e^{v}}{1 + e^{v}}]\\ \\ \Rightarrow [\frac{v+e^{v}}{1+e^{v}}]dv = -\frac{dy}{y}\)
Integrate on both the sides, we get:
\(log(v+e^{v})=-logy+logC=log(\frac{C}{y})\\ \\ \Rightarrow [\frac{x}{y}+e^{\frac{x}{y}}]=\frac{C}{y}\\ \\ \Rightarrow x+ye^{\frac{x}{y}}=C\\\)This is the required solution of the given differential equation.
Q.11: ( x + y )dy + ( x – y )dx = 0 ; y = 1 when x = 1
Ans: Based on the formula given under DIFFERENTIAL EQUATIONS
(x + y)dy + (x – y)dx = 0
\(\boldsymbol{\Rightarrow }\) ( x + y )dy = -( x – y )dx
\(\boldsymbol{\Rightarrow }\) \(\frac{dy}{dx}=\frac{-(x-y)}{x+y}\) . . . . . . . . . . . . (1)
Let, F( x , y ) = \(\frac{-(x-y)}{x+y}\)
Therefore, \(F( \lambda x,\lambda y) = \frac{-(\lambda x – \lambda y)}{\lambda x + \lambda y} = \frac{-( x- y)}{ x + y} =\lambda ^{0}\cdot F(x , y)\)
We observed that equation (1) is a homogeneous equation as follows.
Let, y=vx
Differentiate both the sides w.r.t. x, we get:
\(\Rightarrow \frac{d}{dx}(y)=\frac{d}{dx}(vx)\) \(\frac{dy}{dx}=v+x\frac{dv}{dx}\\\)Substitute the values of v and \(\frac{dy}{dx}\) in equation(1), we get as follows:
\(\boldsymbol{\Rightarrow }\) \(v+x\frac{dv}{dx} = \frac{-(x-vx)}{x+vx}\\ \\ \Rightarrow v+x\frac{dv}{dx} = \frac{v-1}{v+1}\\ \\ x\frac{dv}{dx} = \frac{v-1}{v+1}-v\\ \\ x\frac{dv}{dx} = \frac{v-1-v(v+1)}{v+1}\\ \\ x\frac{dv}{dx} = \frac{v-1-v^{2}-v}{v+1} = \frac{-(1+v^{2})}{v+1}\\ \\ \Rightarrow \frac{(v+1)}{1+v^{2}}dv = -\frac{dx}{x}\\ \\ \Rightarrow [\frac{v}{1+v^{2}}+\frac{1}{1+v^{2}}]dv = -\frac{dx}{x}\\\)
Integrate on bothe the sides, we get:
\(\\\boldsymbol{\Rightarrow }\) \(\frac{1}{2}log(1 + v^{2}) + tan^{-1}v = -logx+k\\ \\ \Rightarrow log(1 + v^{2}) + 2tan^{-1}v = -2logx+2k\\ \\ \Rightarrow log[(1 + v^{2})\cdot x^{2}] + 2tan^{-1}v = 2k\\ \\ \Rightarrow log[(1 + \frac{y^{2}}{x^{2}})\cdot x^{2}] + 2tan^{-1}\frac{y}{x} = 2k\\ \\ \Rightarrow log(x^{2} + y^{2}) + 2tan^{-1}\frac{y}{x} = 2k\) …..(2)
Now y = 1 at x = 1:
\(\Rightarrow log 2 + 2tan^{-1}1 = 2k\\ \\ \Rightarrow log2 + 2\times \frac{\pi }{4} = 2k\\ \\ \Rightarrow \frac{\pi }{2} + log2 = 2k\\\)Substitute value of 2k in equn(2), we get:
\(log(x^{2} + y^{2}) + 2tan^{-1}(\frac{y}{x}) = \frac{\pi }{2} + log2\)This is the required solution of the given differential equation.
Q.12: x2 dy + ( xy + y2 )dx = 0, y = 1 when x =1
Ans: Based on the formula given under DIFFERENTIAL EQUATIONS
x2 dy + ( xy + y2 )dx = 0
\(\Rightarrow x^{2}dy = -(xy+y^{2})dx\\ \\ \Rightarrow \frac{dy}{dx} = \frac{-(xy+y^{2})}{x^{2}}\) . . . . . . . . . . . . (1)
Let F(x, y) = \(\frac{-(xy+y^{2})}{x^{2}}\)
Therefore, \(F( \lambda x , \lambda y ) \frac{ -( \lambda x \cdot \lambda y + (\lambda y)^{2})}{(\lambda x)^{2}} = \frac{-(xy+y^{2})}{x^{2}} = \lambda ^{0}\cdot F (x , y )\)
Here we have observed that equation (1) is a homogeneous equation as follows.
Let, y = vx
Differentiate both the sides w.r.t. x, we get:
\(\Rightarrow \frac{d}{dx}(y)=\frac{d}{dx}(vx)\) \(\frac{dy}{dx}=v+x\frac{dv}{dx}\)Substitute the values of v and \(\frac{dy}{dx}\) in equation(1), we get:
\(\boldsymbol{\Rightarrow }\) \(v+x\frac{dv}{dx} = \frac{ -[x\cdot vx + ( vx )^{2}]}{ x^{2}} = -v-v^{2}\\ \\ \Rightarrow x\frac{dv}{dx} = -v^{2}-2v = -v( v + 2 )\\ \\ \Rightarrow \frac{dv}{v ( v + 2 )} = -\frac{dx}{x}\\ \\ \Rightarrow \frac{1}{2}[\frac{( v + 2 ) – v}{v( v + 2 )}]dv = -\frac{dx}{x}\\ \\ \Rightarrow \frac{1}{2}[\frac{1}{v} – \frac{1}{v + 2}]dv = -\frac{dx}{x}\\\)
Integrate on both the sides, we get:
\(\boldsymbol{\Rightarrow }\) \(\frac{1}{2}[logv – log( v + 2 )] = -logx + logC\\ \\ \Rightarrow \frac{1}{2}log(\frac{v}{v+2}) = log\frac{C}{x}\\ \\ \Rightarrow \frac{v}{v + 2} = (\frac{C}{x})^{2}\\ \\ \Rightarrow \frac{\frac{y}{x}}{\frac{y}{x}+2} = (\frac{C}{x})^{2}\\ \\ \Rightarrow \frac{y}{y + 2x} = \frac{C^{2}}{x^{2}}\\ \\ \frac{x^{2}y}{y+2x} = C^{2}\) . . . . . . . . . . . . (2)
Now, y = 1 at x = 1:
\(\Rightarrow \frac{1}{1 + 2} = C^{2}\\ \\ \Rightarrow C^{2} = \frac{1}{3}\)Substituting C2 = \(\frac{1}{3}\)
\(\frac{x^{2}y}{y + 2x} = \frac{1}{3}\\ \\ \Rightarrow y + 2x = 3x^{2}y\)This is the required solution for the given differential equation.
Q.13: \([xsin^{2}(\frac{x}{y}-y)]dx+xdy=0;\, y=\frac{\pi }{4}\, when\, x=1\)
Ans: Based on the formula given under DIFFERENTIAL EQUATIONS
\([xsin^{2}(\frac{x}{y}-y)]dx+xdy=0\\ \\ \Rightarrow \frac{dy}{dx}=\frac{-[xsin^{2}(\frac{y}{x})-y]}{x}\\ \\\) . . . . . . . . . . . . . . (1)
Let, F(x , y) = \(\frac{-[xsin^{2}(\frac{y}{x})-y]}{x}\)
Therefore, \(F(\lambda x,\lambda y)\frac{-[\lambda x\cdot sin^{2}(\frac{\lambda x}{\lambda y})-\lambda y]}{\lambda x} = \frac{-[xsin^{2}(\frac{y}{x})-y]}{x} = \lambda ^{0}\cdot F(x,y)\)
So, the given differential equation is a homogeneous equation.
Let y = vx
Differentiate both the sides w.r.t. x, we get
\(\Rightarrow \frac{d}{dx}(y)=\frac{d}{dx}(vx)\) \(\frac{dy}{dx}=v+x\frac{dv}{dx}\\\)Substitute the values of v and \(\frac{dy}{dx}\) in equation(1), we get:
\(\boldsymbol{\Rightarrow }\) \(v+x\frac{dv}{dx} = \frac{-[xsin^{2}v-vx]}{x}\\ \\ \Rightarrow v+x\frac{dv}{dx} = -[sin^{2}v-v] = v – sin^{2}v\\ \\ \Rightarrow x\frac{dv}{dx } = -sin^{2}v\\ \\ \Rightarrow \frac{dv}{sin^{2}v} = -\frac{dx}{x}\\ \\ \Rightarrow cosec^{2}vdv = -\frac{dx}{x}\)
Integrate on both the sides, we get:
\(\boldsymbol{\Rightarrow }\) -cot v = -log|x|- C
\(\Rightarrow cot v=log\left | x \right |+C\\ \\ \Rightarrow cot (\frac{y}{x})=log\left | x \right |+logC\\ \\ \Rightarrow cot (\frac{y}{x})=log\left |Cx \right |\\\) . . . . . . . . . . . (2)
Now, y = \(\frac{\pi }{4}\) at x = 1
\(\boldsymbol{\Rightarrow }\) \(\cot\frac{\pi }{4} = log\left | C \right |\)
\(\boldsymbol{\Rightarrow }\) 1 = log C
\(\boldsymbol{\Rightarrow }\) C = e1 = e
Substituting C = e in equation (2), we get:
\(cot(\frac{y}{x})=log\left | ex \right |\\\)This is the required solution for the given differential equation.
Q.14: \(\frac{dy}{dx}-\frac{y}{x}+cosec(\frac{y}{x})=0;y=0\:when\:x=1\)
Ans: Based on the formula given under DIFFERENTIAL EQUATIONS
\(\frac{dy}{dx}-\frac{y}{x}+cosec(\frac{y}{x})=0\\ \\ \Rightarrow \frac{dy}{dx}=\frac{y}{x}-cosec(\frac{y}{x})\) . . . . . . . . . . . (1)
Let, F(x , y) = \(\frac{y}{x}-cosec(\frac{y}{x})\)
Therefore, \(F(\lambda x,\lambda y)=\frac{\lambda y}{\lambda x}-cosec(\frac{\lambda y}{\lambda x})\)
\(\boldsymbol{\Rightarrow }\) \(F(\lambda x,\lambda y)=\frac{ y}{ x}-cosec(\frac{ y}{ x})=F(x,y)=\lambda ^{0}\cdot F(x,y)\)
So, the given differential equation is a homogeneous equation.
Let, y = vx
Differentiate both the sides w.r.t. x, we get
\(\Rightarrow \frac{d}{dx}(y)=\frac{d}{dx}(vx)\) \(\frac{dy}{dx}=v+x\frac{dv}{dx}\\\)Substitute the values of v and \(\frac{dy}{dx}\) in equation(1), we get:
\(\boldsymbol{\Rightarrow }\) \(v+x\frac{dv}{dx}=v-cosec\,v\\ \\ \Rightarrow -\frac{dv}{cosec\,v}=-\frac{dx}{x}\\ \\ \Rightarrow -sin\,vdv=\frac{dx}{x}\)
Integrate on both the sides, we get:
\(\boldsymbol{\Rightarrow }\) \(cos\,v = log\,x+log\,C = log\left | Cx \right |\\ \\ \Rightarrow cos(\frac{y}{x}) = log\left | Cx \right |\) . . . . . . . . . . . . . . . . . (2)
This is the required solution for the given differential equation.
Now, y = 0 at x = 1
\(\boldsymbol{\Rightarrow }\) \(cos(0)=log\;C\)
\(\boldsymbol{\Rightarrow }\) 1 = log C
\(\boldsymbol{\Rightarrow }\) C = e1 = e
This is the required solution for the given differential equation.
Q.15: \(2xy+y^{2}-2x^{2}\frac{dy}{dx}=0;\,y=2\:when\:x=1\)
Ans: Based on the formula given under DIFFERENTIAL EQUATIONS
\(2xy+y^{2}-2x^{2}\frac{dy}{dx}=0\)\(\Rightarrow 2x^{2}\frac{dy}{dx}=2xy+y^{2}\\ \\ \Rightarrow \frac{dy}{dx}=\frac{2xy+y^{2}}{2x^{2}}\) . . . . . . . . . . . . (1)
Let, F( x , y ) = \(\frac{2xy+y^{2}}{2x^{2}}\\\)
Therefore, \(F(\lambda x,\lambda y)=\frac{2(\lambda x)(\lambda y)+(\lambda y)^{2}}{2(\lambda x)^{2}}=\frac{2xy+y^{2}}{2x^{2}}=\lambda ^{0}\cdot F(x,y)\)
So, the given differential equation is a homogeneous equation.
Let, y=vx
Differentiate both the sides w.r.t. x, we get:
\(\boldsymbol{\Rightarrow }\) \(\frac{d}{dx}(y)=\frac{d}{dx}(vx)\)
\(\frac{dy}{dx}=v+x\frac{dv}{dx}\\\)Substitute the values of v and \(\frac{dy}{dx}\) in equation(1), we get:
\(\boldsymbol{\Rightarrow }\) \(v + x\frac{dv}{dx} = \frac{2x(vx)_(vx)^{2}}{2x^{2}}\\ \\ \Rightarrow v + x\frac{dv}{dx} = \frac{2v+v^{2}}{2}\\ \\ \Rightarrow v+x\frac{dv}{dx} = v + \frac{v^{2}}{2}\\ \\ \Rightarrow \frac{2}{v^{2}}dv = \frac{dx}{x}\)
Integrate on both the sides, we get:
\(\boldsymbol{\Rightarrow }\) \(2\cdot \frac{v^{-2+1}}{-2+1} = log\left | x \right |+C\\ \\ \Rightarrow -\frac{2}{v} = log\left | x \right |+C\\ \\ \Rightarrow -\frac{2}{\frac{y}{x}} = log\left | x \right |+C\\ \\ \Rightarrow -\frac{2x}{y} = log\left | x \right |+C\) . . . . . . . . . . . (2)
Now, y = 2 at x = 1
\(\boldsymbol{\Rightarrow }\) -1 = log(1)+C
\(\boldsymbol{\Rightarrow }\) C = -1
Substutute C = -1 in equation (2), we get:
\(\boldsymbol{\Rightarrow }\) \(-\frac{2x}{y}=log\left | x \right |-1\\ \\ \Rightarrow \frac{2x}{y}=1-log\left | x \right |\\ \\ \Rightarrow y=\frac{2x}{1-log\left | x \right |},(x\neq 0,x\neq e)\\\)
This is the required solution of the given differential equation.
Q.16: A homogeneous differential equation of the form \(\frac{dx}{dy}=h(\frac{x}{y})\) can be solved by making the substitution
(i) y = vx
(ii) v = yx
(iii) x = vy
(iv) x = v
Ans: Based on the formula given under DIFFERENTIAL EQUATIONS
For solving the homogeneous equation of the form \(\frac{dx}{dy}=h(\frac{x}{y})\) , make the substitution as x = vy. Hence, the correct answer is (iii).
Q.17: Which of the following is a homogeneous differential equation?
(i) (4x + 6y + 5)dy – (3y + 2x + 4)dx = 0
(ii) (xy)dx – (x3 + y3)dy = 0
(iii) (x3 + 2y2)dx + 2xy dy = 0
(iv) y2 dx + (x2 –xy2 – y2)dy = 0
Ans: Based on the formula given under DIFFERENTIAL EQUATIONS
Function F(x, y) is said homogenous function of degree n, if
F( λx , λy ) = λn F(x, y) for any non-zero constant (λ).
Consider the equation given in alternative IV:
Y2 dx + ( x2 – xy –y2 )dy = 0
\(\boldsymbol{\Rightarrow }\) \(\frac{dy}{dx}=\frac{-y^{2}}{x^{2}-xy-y^{2}}=\frac{y^{2}}{y^{2}+xy-x^{2}}\\\)
Let F( x , y ) = \(\frac{y^{2}}{y^{2}+xy-x^{2}}\)
\(\boldsymbol{\Rightarrow }\) \(F(\lambda x,\lambda y) = \frac{(\lambda y)^{2}}{(\lambda y)^{2}+(\lambda x)(\lambda y)-(\lambda x)^{2}} = \frac{\lambda ^{2}y^{2}}{\lambda ^{2}(y^{2}+xy-x^{2})}\)
\(\\\boldsymbol{\Rightarrow }\) \(\lambda ^{0}(\frac{y^{2}}{y^{2}+xy-x^{2}}) = \lambda ^{0}\cdot F(x,y)\)
Hence, the differential equation given in alternative (iv) is a homogenous equation.
Exercise-9.6
Q.1: \(\frac{dy}{dx}+2y = sin\,x\)
Ans: Based on the formula given under DIFFERENTIAL EQUATIONS
Given:
\(\frac{dy}{dx}+2y = sin\,x\)We know that:
\(\frac{dy}{dx}+py=Q\) [where, p = 2 and Q = sin x]
Now, I.F = \(e^{\int pdx}=e^{\int 2dx}=e^{2x}\)
The solution of the given differential equation is given by the relation as follows:
Y(I.F.) = \(\int (Q\times I.F.)dx+C\)
\(\\\boldsymbol{\Rightarrow }\) \(ye^{2x}=\int sinx\cdot e^{2x}dx+C\\\) . . . . . . . . . . (1)
Let, I = \(\int sinx\cdot e^{2x}\)
\(\\\boldsymbol{\Rightarrow }\) \(I=sinx.\int e^{2x} dx-\int (\frac{d}{dx}(sinx).\int e^{2x}dx)dx\\ \\ \Rightarrow I=sinx. \frac{e^{2x}}{2}-\int (cosx.\frac{e^{x}}{2})dx\\ \\ \Rightarrow I=\frac{e^{2x}.sinx}{2}-\frac{1}{2}[cosx.\int e^{2x}-\int (\frac{d}{dx}(cosx).\int e^{2x}dx)dx]\\ \\ \Rightarrow I=\frac{e^{2x}.sinx}{2}-\frac{1}{2}[cosx. \frac{e^{2x}}{2}-\int [(-sinx).\frac{e^{2x}}{2}dx] \\ \Rightarrow I=\frac{e^{2x}.sinx}{2}-\frac{e^{2x}.cosx}{4}-\frac{1}{4}\int (sin.x.e^{2x})dx\\ \\ \Rightarrow I= \frac{e^{2x}}{4}(2sinx-cosx)-\frac{1}{4}I\\ \\ \Rightarrow \frac{5}{4}I=\frac{e^{2x}}{4}(2sinx-cosx)\\ \\ \Rightarrow I=\frac{e^{2x}}{5}(2sinx-cosx)\)
So, equation (1) becomes:
\(ye^{2x}=\frac{e^{2x}}{5}(2sinx-cosx)+C\)\(\\\boldsymbol{\Rightarrow }\) \(y=\frac{1}{5}(2sinx-cosx)+Ce^{-2x}\)
This is the required general solution of the given differential equation.
Q.2: \(\frac{dy}{dx}+3y=e^{-2x}\)
Ans: Based on the formula given under DIFFERENTIAL EQUATIONS
The given differential equation is as follows:
\(\frac{dy}{dx}+py=Q\) (where p=3 and Q=\(e^{-2x}\))
Now, I.F = \(e^{\int pdx}=e^{\int 3dx}=e^{3x}\)
The solution of the given differential equation is given by the relation as follows:
\(y(I.F.)=\int (Q\times I.F.)dx+C\\ \\ \Rightarrow ye^{3x}=\int (e^{-2x}\times e^{3x})+C\\ \\ \Rightarrow ye^{3x}=\int e^{x}dx+C\\ \\ \Rightarrow ye^{3x}=e^{x}+C\\ \\ \Rightarrow y=e^{-2x}+Ce^{-3x}\)This is the required general solution of the given differential equation.
Q.3: \(\frac{dy}{dx}+\frac{y}{x}=x^{2}\)
Ans: Based on the formula given under DIFFERENTIAL EQUATIONS
The given differential equation is as follows:
\(\frac{dy}{dx}+py=Q\) (where p=\(\frac{1}{x}\) and Q = \(x^{2}\))
Now, I.F. = \(e^{\int pdx}=e^{\int \frac{1}{x}dx}=e^{logx}=x\)
The solution of the given differential equation is given by the relation:
\(y(I.F.)=\int (Q\times I.F.)dx+C\)\(\\\boldsymbol{\Rightarrow }\) \(y(x)=\int (x^{2}.x)dx+C\\ \\ \Rightarrow xy=\int x^{3}dx+C\\ \\ \Rightarrow xy=\frac{x^{4}}{4}+C\)
This is the required general solution of the given differential equation.
Q.4: \(\frac{dy}{dx}+sec\,xy=tan\,x(0\leq x< \frac{\pi }{2})\)
Ans: Based on the formula given under DIFFERENTIAL EQUATIONS
The given differential equation is as follows:
\(\frac{dy}{dx}+py=Q\) (where p = sec x and Q = tan x)
Now,
Now, I.F. = \(e^{\int pdx}=e^{\int sec x dx}=e^{log (sec x + tanx) }=sec x+tan x\)
The general solution of the given differential equation is given by the relation:
\(y(I.F.)=\int (Q\times I.F.)dx+C\)\(\\\boldsymbol{\Rightarrow }\) \(y(sec\,x+tan\,x)=\int tan\,x(sec\,x+tan\,x)dx+C\\ \\ \Rightarrow y(sec\,x+tan\,x)=\int sec\,x\,tan\,xdx+\int tan^{2}xdx+C\\ \\ \Rightarrow y(sec\,x+tan\,x)=sec\,x+\int (sec^{2}x-1)dx+C\\ \\ \Rightarrow y(sec\,x+tan\,x)=sec\,x+tan\,x-x+C\)
Q.5: \(\int_{0}^{\frac{\pi }{2}}cos\,2x\,dx\)
Ans: Based on the formula given under DIFFERENTIAL EQUATIONS
Let, I = \(\int_{0}^{\frac{\pi }{2}}cos\,2x\,dx\)
\(\int cos\,2x\,dx=(\frac{sin\,2x}{2})=F(x)\\\)By second fundamental theorem of calculus, we get as follows:
\(I=F(\frac{\pi }{2})-F(0)\\ \\ =\frac{1}{2}[Sin2(\frac{\pi }{2})-sin\,0]\\ \\ =\frac{1}{2}[sin\,\pi -sin\,0]\\ \\ =\frac{1}{2}[0-0]=0\)
Q.6: \(x\frac{dy}{dx}+2y=x^{2}log\,x\)
Ans: Based on the formula given under DIFFERENTIAL EQUATIONS
The given differential equation is:
\(x\frac{dy}{dx}+2y=x^{2}log\,x\)\(\\\boldsymbol{\Rightarrow }\) \(\frac{dy}{dx}+\frac{2}{x}y=xlog\,x\)
This equation is in the form of a linear differential equation as:
\(\frac{dy}{dx}+py=Q\) (where p = \(\frac{2}{x}\) and Q = x log x)
Now, I.F. = \(e^{\int pdx}=e^{\int \frac{2}{x}dx}=e^{2logx}=e^{logx^{2}}=x^{2}\)
The general solution of the given differential equation is given by the relation:
\(y(I.F.)=\int (Q\times I.F.)dx+C\)\(\\\boldsymbol{\Rightarrow }\) \(y.x^{2}=\int (xlogx.x^{2})dx+C\\ \\ \Rightarrow x^{2}y=\int (x^{3}logx)dx+C\\ \\ \Rightarrow x^{2}y=log\,x.\int x^{3}-\int [\frac{d}{dx}(logx).\int x^{3}dx]dx+C\\ \\ \Rightarrow x^{2}y=log\,x.\frac{x^{4}}{4}-\int (\frac{1}{x}.\frac{x^{4}}{4})dx+C\\ \\ \Rightarrow x^{2}y=\frac{x^{4}logx}{4}-\frac{1}{4}\int x^{3}dx+C\\ \\ \Rightarrow x^{2}y=\frac{x^{4}logx}{4}-\frac{1}{4}.\frac{x^{4}}{4}+C\\ \\ \Rightarrow x^{2}y=\frac{1}{16}x^{4}(4logx-1)+C\\ \\ \Rightarrow y=\frac{1}{16}x^{2}(4logx-1)+Cx^{2}\)
Q.7: \(x\;log\;x\frac{dy}{dx}+y=\frac{2}{x}log\;x\)
Ans: Based on the formula given under DIFFERENTIAL EQUATIONS
The given differential equation is:
\(x\;log\;x\frac{dy}{dx}+y=\frac{2}{x}log\;x\) \(\Rightarrow \frac{dy}{dx}+\frac{y}{x\;log\;x}=\frac{2}{x^{2}}\)This equation is the form of a linear differential equation as as follows:
\(\frac{dy}{dx}+py=Q\) (where p = \(\frac{1}{x\;log\;x}\) and Q = \(\frac{2}{x^{2}}\))
Now, I.F. = \(e^{\int pdx}=e^{\int \frac{1}{x\;log\;x}dx}=e^{log\;(log\;x)}=log\,x\)
The general solution of the given differential equation is given by the relation as follows:
\(y(I.F.)=\int (Q\times I.F.)dx+C\)\(\\\boldsymbol{\Rightarrow }\) \(y\;log\;x=\int (\frac{2}{x^{2}}log\;x)\;dx+C\) . . . . . . . . . . . (1)
Now,
\(\int (\frac{2}{x^{2}}logx)dx=2\int (logx.\frac{1}{x^{2}})dx:\)\(\\\boldsymbol{\Rightarrow }\) \(=2[log\,x.\int \frac{1}{x^{2}}dx-\int \left \{ \frac{d}{dx}(logx).\int \frac{1}{x^{2}} dx\right \}dx]\\ \\ =2[log x(-\frac{1}{x})-\int (\frac{1}{x}.(-\frac{1}{x}))dx]\\ \\ =2[-\frac{logx}{x}+\int\frac{1}{x^{2}}dx ]\\ \\ =2[-\frac{logx}{x}-\frac{1}{x}]\\ \\ =-\frac{2}{x}(1+logx)\)
Substituting the value of \(\int (\frac{2}{x^{2}}logx)dx\) in equation (1), we get:
y log x = \(-\frac{2}{x}(1+logx)+C\)
This is the required general solution of the given differential equation.
Q.8.( 1 + x2 )dy+ 2xy dx = cot xdx
Ans: Based on the formula given under DIFFERENTIAL EQUATIONS
\(\Rightarrow \frac{dy}{dx}+\frac{2xy}{1+x^{2}}=\frac{cot\,x}{1+x^{2}}\)This equation is a linear differential equation of the form as follows:
\(\frac{dy}{dx}+py=Q\) (where p = \(\frac{2x}{1+x^{2}}\) and Q = \(\frac{cot\,x}{1+x^{2}}\))
Now, I.F. = \(e^{\int pdx}=e^{\int \frac{2x}{1+x^{2}}dx}=e^{log(1+x^{2})}=1+x^{2}\)
The general solution of the given differential equation is given by the relation as follows:
\(y(I.F.)=\int (Q\times I.F.)dx+C\)\(\\\boldsymbol{\Rightarrow }\) \(y(1+x^{2})=\int [\frac{cot\,x}{1+x^{2}}\times (1+x^{2})]dx+C\\ \\ \Rightarrow y(1+x^{2})=\int cot\,xdx+C\\ \\ \Rightarrow y(1+x^{2})=log\left | sin\,x \right |+C\)
Q.9: \(x\frac{dy}{dx}+y-x+xy\,cot\,x=0(x\neq 0)\)
Ans: Based on the formula given under DIFFERENTIAL EQUATIONS
\(x\frac{dy}{dx}+y-x+xy\,cot\,x=0\)\(\\\boldsymbol{\Rightarrow }\) \(x\frac{dy}{dx}+y(1+x\,cot\,x)=x\)
\(\\\boldsymbol{\Rightarrow }\) \(\frac{dy}{dx}+(\frac{1}{x}+cot\,x)y=1\)
This equation is a linear differential equation of the form as follows:
\(\frac{dy}{dx}+py=Q\) (where p = \(\frac{1}{x}+cot\,x\) and Q = 1)
Now, I.F. = \(e^{\int pdx}=e^{\int (\frac{1}{x}+cot\,x)dx}=e^{log\,x+log(sin\,x)}=e^{log(xsinx)}=x\,sin\,x\)
The general solution of the given differential equation is given by the relation as follows,
\(y(I.F.)=\int (Q\times I.F.)dx+C\\\)\(\\\boldsymbol{\Rightarrow }\) \(y(xsinx)=\int (1\times xsinx)dx+C\\ \\ \Rightarrow y(xsinx)=\int ( xsinx)dx+C\\ \\ \Rightarrow y(xsinx)=x\int sinx\,dx-\int [\frac{d}{dx}(x).\int sinx\,dx]+C\\ \\ \Rightarrow y(xsinx)=x(-cos\,x)-\int 1.(-cos\,x)dx+C\\ \\ \Rightarrow y(xsinx)=-xcosx+sinx+C\\ \\ \Rightarrow y=\frac{-xcosx}{xsinx}+\frac{sinx}{xsinx}+\frac{C}{xsinx}\\ \\ \Rightarrow y=-cotx+\frac{1}{x}+\frac{C}{xsinx}\)
Q.10: \((x+y)\frac{dy}{dx}=1\)
Ans: Based on the formula given under DIFFERENTIAL EQUATIONS
\((x+y)\frac{dy}{dx}=1\)\(\\\boldsymbol{\Rightarrow }\) \(\frac{dy}{dx}=\frac{1}{x+y}\\ \\ \Rightarrow \frac{dx}{dy}=x+y\\ \\ \Rightarrow \frac{dx}{dy}-x=y\)
This is a linear differential equation of the form:
\(\frac{dy}{dx}+py=Q\) (where p = -1 and Q = y)
Now, I.F. = \(e^{\int pdx}=e^{\int –dy}=e^{-y}\)
The general solution of the given differential equation is given by the relation:
\(y(I.F.)=\int (Q\times I.F.)dx+C\) \(\Rightarrow xe^{-y}=\int (y.e^{-y})dy+C\\ \\ \Rightarrow xe^{-y}=y.\int e^{-y}dy-\int [\frac{d}{dy}(y)\int e^{-y}dy]dy+C\\ \\ \Rightarrow xe^{-y}=y(-e^{-y})-\int (-e^{-y})dy+C\\ \\ \Rightarrow xe^{-y}=-ye^{-y}+\int e^{-y}dy+C\\ \\ \Rightarrow xe^{-y}=-ye^{-y}- e^{-y}+C\\ \\ \Rightarrow x=-y-1+Ce^{y}\\ \\ \Rightarrow x+y+1=Ce^{y}\)
Q.11: y dx + ( x – y2 )dy = 0
Ans: Based on the formula given under DIFFERENTIAL EQUATIONS
y dx + ( x – y2 )dy = 0
\(\Rightarrow ydx=(y^{2}-x)dy\\ \\ \Rightarrow \frac{dx}{dy}=\frac{y^{2}-x}{y}=y-\frac{x}{y}\\ \\ \Rightarrow \frac{dx}{dy} + \frac{x}{y} = y\\\)This is a linear differential equation of the form:
\(\frac{dy}{dx}+py=Q\) (where p = \(\frac{1}{y}\) and Q = y)
Now, I.F. = \(e^{\int pdx}=e^{\int \frac{1}{y}dy}=e^{logy}=y\)
The general solution of the given differential equation is given by the relation:
\(x\;(I.F.)=\int (Q\times I.F.)dy+C\)\(\\\boldsymbol{\Rightarrow }\) \(xy=\int (y.y)dy+C\)
\(\\\boldsymbol{\Rightarrow }\) \(xy=\int y^{2}dy+C = \frac{y^{3}}{3}+C\)
\(\\\boldsymbol{\Rightarrow }\) \(x=\frac{y^{3}}{3}+\frac{C}{y}\)
Q.12: \((x+3y^{2})\frac{dy}{dx}=y(y>0)\)
Ans: Based on the formula given under DIFFERENTIAL EQUATIONS
\((x+3y^{2})\frac{dy}{dx}=y\)\(\\\boldsymbol{\Rightarrow }\) \(\frac{dy}{dx}=\frac{y}{x+3y^{2}}\)
\(\\\boldsymbol{\Rightarrow }\) \(\frac{dx}{dy}=\frac{x+3y^{2}}{y}=\frac{x}{y}+3y\)
\(\\\boldsymbol{\Rightarrow }\) \(\frac{dx}{dy} – \frac{x}{y}=3y\)
This is a linear differential equation of the form as follows:
\(\frac{dx}{dy}+px=Q\) [where, p = \(-\frac{1}{y}\) and Q = 3y]
Now, I.F. = \(e^{\int pdx}=e^{-\int \frac{dy}{y}}=e^{-logy}= e^{\frac{1}{y}}= \frac{1}{y}\)
The general solution of the given differential equation is given by the relation:
\(x\;(I.F.)=\int (Q\times I.F.)dy+C\)\(\\\boldsymbol{\Rightarrow }\) \(x\times \frac{1}{y}=\int (3y\times \frac{1}{y})dy+C\)
\(\boldsymbol{\Rightarrow }\) \(\frac{x}{y}=3y+C\)
\(\boldsymbol{\Rightarrow }\) x = 3y2 + Cy
Q.13: \(\frac{dy}{dx}+2y\,tanx=sin\,x;y=0\:when\,x=\frac{\pi }{3}\)
Ans: Based on the formula given under DIFFERENTIAL EQUATIONS
Given:
\(\frac{dy}{dx}+2y\,tanx=sin\,x\)This is a linear equation of the form as follows:
\(\frac{dy}{dx}+py=Q\) (where p = 2 tan x and Q = sin x)
Now, I.F.= \(e^{\int pdx}=e^{\int 2tan\,x dx}=e^{2log\left | secx \right |}=e^{log(sec^{2}x)}=sec^{2}x\)
The general solution of the given differential equation is given by the relation as follows,
\(y(I.F.)=\int (Q\times I.F.)dx+C\)\(\Rightarrow y(sec^{2}x)=\int (sin\,x.sec^{2}x)dx+C\\ \\ \Rightarrow y\,sec^{2}x=\int (sec\,x.tan\,x)dx+C\\ \\ \Rightarrow y\,sec^{2}x=sec\,x+C\) …….(1)
Now, y = 0 at \(x=\frac{\pi }{3}\)
Therefore,
\(0\times sec^{2}\frac{\pi }{3}=sec\frac{\pi }{3}+C\)0 = 2 + C i.e C= – 2
Substituting C = –2 in equation (1), we get:
y sec2 x = sec x – 2
\(\boldsymbol{\Rightarrow }\) y = cos x – 2cos2 x
Hence, the required solution of the given differential equation is y = cos x – 2cos2 x
Q.14.\((1+x^{2})\frac{dy}{dx}+2xy=\frac{1}{1+x^{2}};y=0\:when\,x=1\)
Ans: Based on the formula given under DIFFERENTIAL EQUATIONS
\((1+x^{2})\frac{dy}{dx}+2xy=\frac{1}{1+x^{2}}\) \(\Rightarrow\frac{dy}{dx}+\frac{2xy}{1+x^{2}}=\frac{1}{(1+x^{2})^{2}}\\\)This is a linear differential equation of the form as follows:
\(\frac{dy}{dx}\) + py = Q [where, p = \(\frac{2x}{1+x^{2}}\) and Q = \(\frac{1}{(1+x^{2})^{2}})\)]
Now, I.F. = \(e^{\int pdx}=e^{\int \frac{2xdx}{1+x^{2}}}=e^{log(1+x^{2})}=1+x^{2}\)
The general solution of the given differential equation is given by the relation as follows:
\(y(I.F.)=\int (Q\times I.F.)dx+C\\\)\(\boldsymbol{\Rightarrow }\) \(y(1+x^{2})=\int [\frac{1}{1+x^{2}}.(1+x^{2})]dx+C\\ \\ \Rightarrow y(1+x^{2})=\int \frac{1}{1+x^{2}}dx+C\\ \\ \Rightarrow y(1+x^{2})=tan^{-1}x+C\) . . . . . . . . . .(1)
Now, y = 0 at x = 1
Therefore,
0 = tan-11 + C
\(\Rightarrow\) C = \(-\frac{\pi }{4}\)
Substitute C = \(-\frac{\pi }{4}\) in equation(1), we get:
y( 1 + x2 ) = tan-1 x – \(\frac{\pi }{4}\)
This is the required general solution of the given differential equation.
Q.15: \(\frac{dy}{dx}-3y\,cot\,x=sin\,2x;y=2\:when\:x=\frac{\pi }{2}\)
Ans: Based on the formula given under DIFFERENTIAL EQUATIONS
Given:
\(\frac{dy}{dx}-3y\,cot\,x=sin\,2x\)This is a linear differential equation of the form as follows:
\(\frac{dy}{dx}\) + py = Q [where, p = -3 cot x and Q = sin 2x]
Now, I.F. = \(e^{\int pdx}=e^{-3\int cot\,x\,dx}=e^{-3log\left | sin\,x \right |}=e^{log\left | \frac{1}{sin^{3}x} \right |}=\frac{1}{sin^{3}x}\)
The general solution of the given differential equation is given by the relation as follows:
\(y(I.F.)=\int (Q\times I.F.)dx+C\\\)\(\\\boldsymbol{\Rightarrow }\) \(y\cdot \frac{1}{sin^{3}x}=\int[sin2x\cdot \frac{1}{sin^{3}x}]dx+C\)
\(\\\boldsymbol{\Rightarrow }\) y cosec3 x = 2 \(\int (cot\;x\;cosec\;x)\) dx + C
\(\\\boldsymbol{\Rightarrow }\) \(y\;cosec^{3}x=2cosec\;x+C \;=\;-\frac{2}{cosec^{2}x}+\frac{3}{cosec^{3}x}\)
\(\\\boldsymbol{\Rightarrow }\) \(y=-2\,sin^{2}x+C\,sin^{3}x\) . . . . . . (1)
Now,
y = 2 at x = \(\frac{\pi }{2}\)
Therefore, we get as follows:
2 = -2 + C
\(\Rightarrow C = 4\)Substitute C = 4 in equation (1), we get:
\(y=-2sin^{2}x+4sin^{3}x\\ \\ \Rightarrow y=4sin^{3}x-2sin^{2}x\)This is the required particular solution of the given differential equation.
Q.16: Find the equation of a curve passing through the origin given that the slope of the tangent to the curve at any point (x, y) is equal to the sum of the coordinates of the point.
Ans: Based on the formula given under DIFFERENTIAL EQUATIONS
Let, F (x , y) be the curve passing through the origin.
At point (x, y), the slope of the curve will be \(\frac{dy}{dx}\).
According to the given information as follows:
\(\frac{dy}{dx}=x+y\\ \\ \Rightarrow \frac{dy}{dx}-y=x\)This is a linear differential equation of the form:
\(\frac{dy}{dx}\) + py = Q [where, p =-1 and Q =x]
Now, I.F. = \(\\e^{\int pdx}=e^{\int(-1)dx }=e^{-1}\)
The general solution of the given differential equation is given by the relation,
\(y\;(I.F.)=\int (Q\times I.F.)\;dx+C\\\)\(\boldsymbol{\Rightarrow }\) \(ye^{-1}=\int xe^{-1}dx+C\) . . . . . . . . . . (1)
Now ,
\(\int xe^{-1}dx=x\int e^{-1}dx-\int [\frac{d}{dx}(x).\int e^{-x}dx]dx\\ \\ =-xe^{-x}-\int -e^{-1}dx\\ \\ =-xe^{-x}(-e^{-x})\\ \\ =-e^{-x}(x+1)\)Substituting in equation (1), we get:
Ye-1 = -e-x ( x + 1 ) + C
\(\Rightarrow\) y = -( x + 1 ) + Cex
\(\Rightarrow\) x + y + 1 = Cex . . . . . . . . . . (2)
The curve passes through the origin.
Therefore, equation (2) becomes as follows:
C = 1
Substituting C = 1 in equation (2), we get:
x + y + 1 = ex
Hence, the required equation of curve passing through the origin is x + y + 1 = ex
Q.17. Find the equation of a curve passing through the point (0, 2) given that the sum of the coordinates of any point on the curve exceeds the magnitude of the slope of the tangent to the curve at that point by 5.
Ans: Based on the formula given under DIFFERENTIAL EQUATIONS
Let, F (x, y) be the curve and let (x, y) be a point on the curve.
The slope of the tangent to the curve at (x, y) is \(\frac{dy}{dx}\).
According to the given information:
\(\frac{dy}{dx}+5=x+y\\ \\ \Rightarrow \frac{dy}{dx}-y=x-5\)This is a linear differential equation of the form as follows:
\(\frac{dy}{dx}\) + py = Q [where, p = -1 and Q = x – 5]
Now, I.F. = \(e^{\int pdx}=e^{\int(-1)dx }=e^{-x}\)
The general equation of the curve is given by the relation as follows:
\(y\;(I.F.)=\int (Q\times I.F.)\;dx+C\)\(\\\boldsymbol{\Rightarrow }\) \(y.e^{-x}=\int (x-5)e^{-x}dx+C \) . . . . . . . . . . . . (1)
Now,
\(\boldsymbol{\Rightarrow }\) \(\int (x-5)e^{-x}dx=(x-5)\int e^{-x}dx-\int \;[\frac{d}{dx}(x-5).\int e^{-x}dx]\)
\(\\\boldsymbol{\Rightarrow }\) \((x-5)(-e^{-x})-\int (-e^{-x})\;dx\)
\(\\\boldsymbol{\Rightarrow }\) \((5-x)e^{-x}+(-e^{-x})\)
\(\\\boldsymbol{\Rightarrow }\) \((4-x)e^{-x}\)
Therefore, equation (1) becomes:
ye-x = ( 4 – x ) e-x + C
\(\boldsymbol{\Rightarrow }\) y = 4 – x + Cex
\(\boldsymbol{\Rightarrow }\) x + y – 4 = Cex . . . . . . . . . . . . . . (2)
The curve passes through point (0, 2).
Therefore, equation (2) becomes as follows:
0 + 2 – 4 = Ce0
\(\boldsymbol{\Rightarrow }\) – 2 = C
or, C = – 2
Substituting C = –2 in equation (2), we get as follows:
x + y – 4 = -2ex
\(\boldsymbol{\Rightarrow }\) y = 4 – x – 2ex
This is the required equation of the curve.
Q.18: The integrating factor of the differential equation \(x\frac{dy}{dx}-y=2x^{2}\) is
(i) e-x
(ii) e-y
(iii) \(\frac{1}{x}\)
(iv) x
Ans: Based on the formula given under DIFFERENTIAL EQUATIONS
The given differential equation is:
\(x\frac{dy}{dx}-y=2x^{2}\)\(\boldsymbol{\Rightarrow }\) \(\frac{dy}{dx}-\frac{y}{x}=2x\)
This is a linear differential equation of the form as follows:
\(\frac{dy}{dx}\) + py = Q [where, p =-\(\frac{1}{x}\) and Q =2x]
The integrating factor (I.F) is given by the relation as follows:
\(\boldsymbol{\Rightarrow }\) \(I.F.=e^{\int \frac{1}{x}dx}=e^{-log\,x}=e^{log(-x)}=x^{-1}=\frac{1}{x}\)
Hence, the correct answer is (iii)
Q.19: The integrating factor of the differential equation.
\((1-y^{2})\frac{dx}{dy}+yx=ay(-1<y<1)\)
(i) \(\frac{1}{y^{2}-1}\)
(ii) \(\frac{1}{\sqrt{y^{2}-1}}\)
(iii) \(\frac{1}{1-y^{2}}\)
(iv) \(\frac{1}{\sqrt{1-y^{2}}}\)
Ans: Based on the formula given under DIFFERENTIAL EQUATIONS
The given differential equation is as follows:
\(\frac{dx}{dy}+yx=ay\)\(\boldsymbol{\Rightarrow }\) \(\frac{dx}{dy}+\frac{yx}{1-y^{2}}=\frac{ay}{1-y^{2}}\\\)
This is a linear differential equation of the form as follows:
\(\frac{dx}{dy}+py=Q(where\:p=\frac{y}{1-y^{2}}\:and\:Q=\frac{ay}{1-y^{2}})\\\)The integrating factor (I.F) is given by the relation as follows:
\(\boldsymbol{\Rightarrow }\) \(I.F.=e^{\int pdy}=e^{\int \frac{y}{1-y^{2}}dy}=e^{-\frac{1}{2}log(1-y^{2})}=e^{log[\frac{1}{\sqrt{1-y^{2}}}]}=\frac{1}{\sqrt{1-y^{}}}\)
Hence, the correct answer is (iv)