1D Numpy in Python

  • Preparation for using Numpy library 


    • 
# Import the libraries

import time 
import sys
import numpy as np 

import matplotlib.pyplot as plt
%matplotlib inline  
# Plotting functions

def Plotvec1(u, z, v):
    
    ax = plt.axes()
    ax.arrow(0, 0, *u, head_width=0.05, color='r', head_length=0.1)
    plt.text(*(u + 0.1), 'u')
    
    ax.arrow(0, 0, *v, head_width=0.05, color='b', head_length=0.1)
    plt.text(*(v + 0.1), 'v')
    ax.arrow(0, 0, *z, head_width=0.05, head_length=0.1)
    plt.text(*(z + 0.1), 'z')
    plt.ylim(-2, 2)
    plt.xlim(-2, 2)

def Plotvec2(a,b):
    ax = plt.axes()
    ax.arrow(0, 0, *a, head_width=0.05, color ='r', head_length=0.1)
    plt.text(*(a + 0.1), 'a')
    ax.arrow(0, 0, *b, head_width=0.05, color ='b', head_length=0.1)
    plt.text(*(b + 0.1), 'b')
    plt.ylim(-2, 2)
    plt.xlim(-2, 2)

  • Create a Python List as follows: 


    • 
# Create a python list

a = ["0", 1, "two", "3", 4]

  • We can access the data via an index:


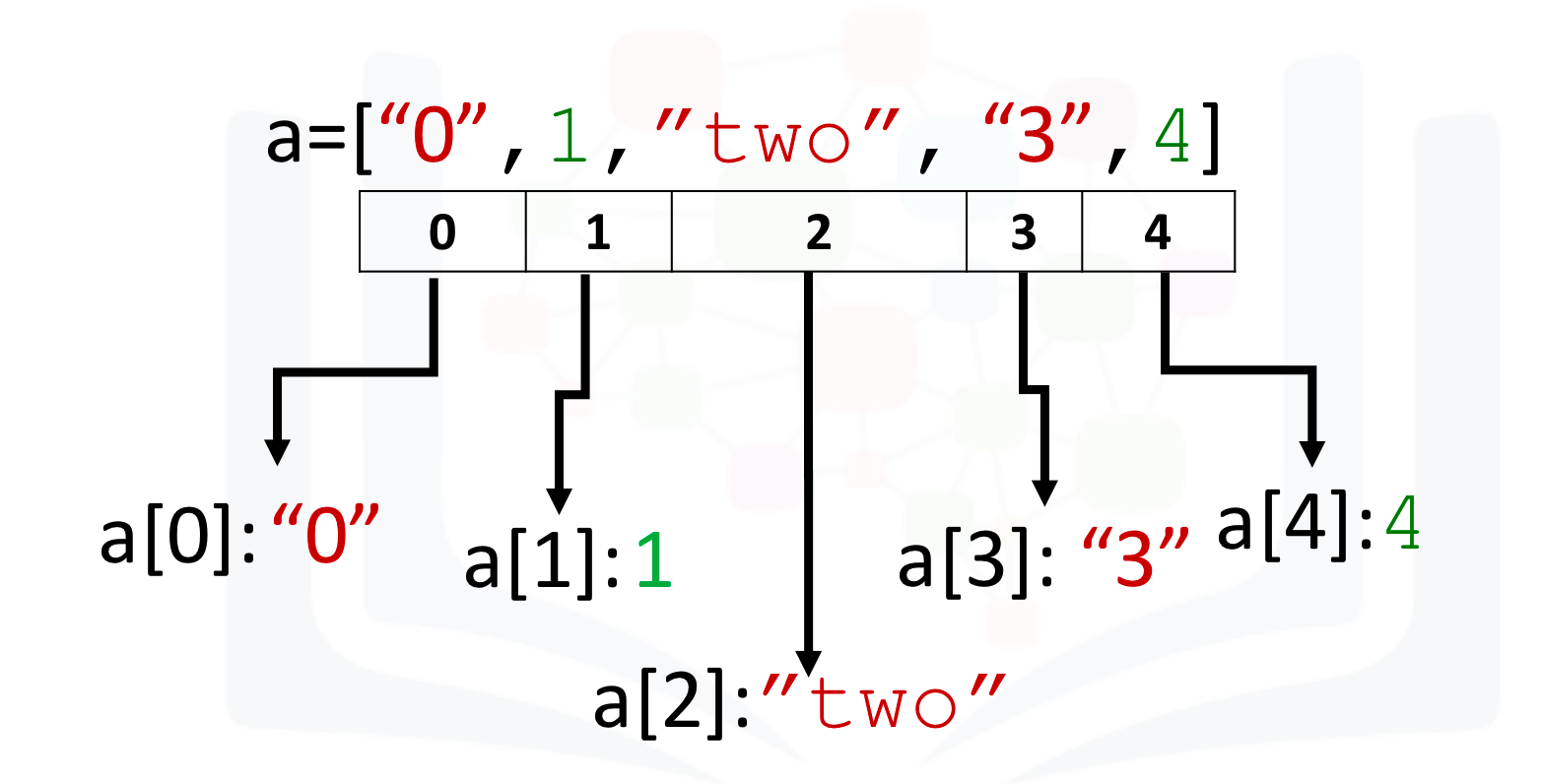
  • Create a numpy array


  • We can access each element using a square bracket as follows: 


    • 
# Print each element

print("a[0]:", a[0])
print("a[1]:", a[1])
print("a[2]:", a[2])
print("a[3]:", a[3])
print("a[4]:", a[4])

  • What is Numpy? A numpy array is similar to a list. It's usually fixed in size and each element is of the same type. We can cast a list to a numpy array by first importing numpy: 


    • 
# import numpy library

import numpy as np

  • We then cast the list as follows: 


    • 
# Create a numpy array

a = np.array([0, 1, 2, 3, 4])
a

  • Each element is of the same type, in this case integers:


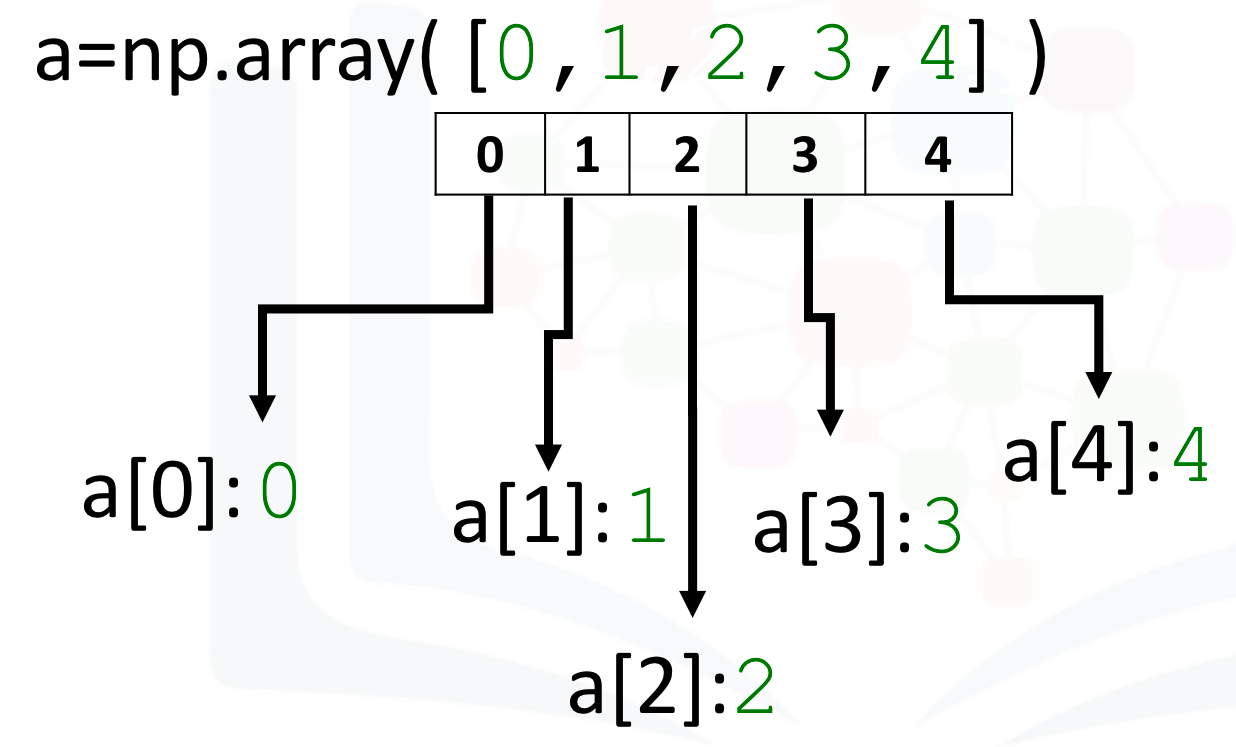
  • Create a numpy array


  • As with lists, we can access each element via a square bracket: 


    • 
# Print each element

print("a[0]:", a[0])
print("a[1]:", a[1])
print("a[2]:", a[2])
print("a[3]:", a[3])
print("a[4]:", a[4])

  • Type If we check the type of the array we get numpy.ndarray: 


    • 
# Check the type of the array

type(a)

  • As numpy arrays contain data of the same type, we can use the attribute "dtype" to obtain the Data-type of the array’s elements. In this case a 64-bit integer: 


    • 
# Check the type of the values stored in numpy array

a.dtype

  • We can create a numpy array with real numbers: 


    • 
# Create a numpy array

b = np.array([3.1, 11.02, 6.2, 213.2, 5.2])

  • When we check the type of the array we get numpy.ndarray: 


    • 
# Check the type of array

type(b)

  • If we examine the attribute dtype we see float 64, as the elements are not integers: 


    • 
# Check the value type

b.dtype

  • Assign value We can change the value of the array, consider the array c: 


    • 
# Create numpy array

c = np.array([20, 1, 2, 3, 4])
c

  • We can change the first element of the array to 100 as follows: 


    • 
# Assign the first element to 100

c[0] = 100
c

  • We can change the 5th element of the array to 0 as follows: 


    • 
# Assign the 5th element to 0

c[4] = 0
c

  • Slicing Like lists, we can slice the numpy array, and we can select the elements from 1 to 3 and assign it to a new numpy array d as follows: 


    • 
# Slicing the numpy array

d = c[1:4]
d

  • We can assign the corresponding indexes to new values as follows: 


    • 
# Set the fourth element and fifth element to 300 and 400

c[3:5] = 300, 400
c

  • Assign Value with List Similarly, we can use a list to select a specific index. The list ' select ' contains several values: 


    • 
# Create the index list

select = [0, 2, 3]

  • We can use the list as an argument in the brackets. The output is the elements corresponding to the particular index: 


    • 
# Use List to select elements

d = c[select]
d

  • We can assign the specified elements to a new value. For example, we can assign the values to 100 000 as follows: 


    • 
# Assign the specified elements to new value

c[select] = 100000
c

  • Other Attributes Let's review some basic array attributes using the array a: 


    • 
# Create a numpy array

a = np.array([0, 1, 2, 3, 4])
a

  • The attribute size is the number of elements in the array: 


    • 
# Get the size of numpy array

a.size

  • The next two attributes will make more sense when we get to higher dimensions but let's review them. The attribute ndim represents the number of array dimensions or the rank of the array, in this case, one: 


    • 
# Get the number of dimensions of numpy array

a.ndim

  • The attribute shape is a tuple of integers indicating the size of the array in each dimension: 


    • 
# Get the shape/size of numpy array

a.shape
 

    
# Create a numpy array

a = np.array([1, -1, 1, -1])
 

    
# Get the mean of numpy array

mean = a.mean()
 

    
# Get the standard deviation of numpy array

standard_deviation=a.std()
standard_deviation
 

    
# Create a numpy array

b = np.array([-1, 2, 3, 4, 5])
b
 

    
# Get the biggest value in the numpy array

max_b = b.max()
max_b
 

    
# Get the smallest value in the numpy array

min_b = b.min()
min_b

  • Numpy Array Operations Array Addition Consider the numpy array u: 


    • 
u = np.array([1, 0])
u

  • Consider the numpy array v: 


    • 
v = np.array([0, 1])
v

  • We can add the two arrays and assign it to z: 


    • 
# Numpy Array Addition

z = u + v
z

  • The operation is equivalent to vector addition: 


    • 
# Plot numpy arrays

Plotvec1(u, z, v)

  • Array Multiplication Consider the vector numpy array y: 


    • 
# Create a numpy array

y = np.array([1, 2])
y

  • We can multiply every element in the array by 2: 


    • 
# Numpy Array Multiplication

z = 2 * y
z

  • This is equivalent to multiplying a vector by a scaler: Product of Two Numpy Arrays Consider the following array u: 


    • 
# Create a numpy array

u = np.array([1, 2])
u

  • Consider the following array v: 


    • 
# Create a numpy array

v = np.array([3, 2])
v

  • The product of the two numpy arrays u and v is given by: 


    • 
# Calculate the production of two numpy arrays

z = u * v
z

  • Dot Product The dot product of the two numpy arrays u and v is given by: 


    • 
# Calculate the dot product

np.dot(u, v)

  • Adding Constant to a Numpy Array Consider the following array: 


    • 
# Create a constant to numpy array

u = np.array([1, 2, 3, -1]) 
u

  • Adding the constant 1 to each element in the array: 


    • 
# Add the constant to array

u + 1

  • The process is summarised in the following animation:


  • Dot Product


  • Mathematical Functions We can access the value of pie in numpy as follows : 


    • 
# The value of pie

np.pi

  • We can create the following numpy array in Radians: 


    • 
# Create the numpy array in radians

x = np.array([0, np.pi/2 , np.pi])

  • We can apply the function sin to the array x and assign the values to the array y; this applies the sine function to each element in the array: 


    • 
# Calculate the sin of each elements

y = np.sin(x)
y

  • Linspace A useful function for plotting mathematical functions is "linespace". Linespace returns evenly spaced numbers over a specified interval. We specify the starting point of the sequence and the ending point of the sequence. The parameter "num" indicates the Number of samples to generate, in this case 5: 


    • 
# Makeup a numpy array within [-2, 2] and 5 elements

np.linspace(-2, 2, num=5)

  • If we change the parameter num to 9, we get 9 evenly spaced numbers over the interval from -2 to 2: 


    • 
# Makeup a numpy array within [-2, 2] and 9 elements

np.linspace(-2, 2, num=9)

  • We can use the function line space to generate 100 evenly spaced samples from the interval 0 to 2π: 


    • 
# Makeup a numpy array within [0, 2π] and 100 elements 

x = np.linspace(0, 2*np.pi, num=100)

  • We can apply the sine function to each element in the array x and assign it to the array y: 


    • 
# Calculate the sine of x list

y = np.sin(x)

# Plot the result

plt.plot(x, y)

2D Numpy in Python

  • Create a 2D Numpy Array 


    • 
# Import the libraries

import numpy as np 
import matplotlib.pyplot as plt

  • Consider the list a, the list contains three nested lists each of equal size. 


    • 
# Create a list

a = [[11, 12, 13], [21, 22, 23], [31, 32, 33]]
a

  • We can cast the list to a Numpy Array as follow 


    • 
# Convert list to Numpy Array
# Every element is the same type

A = np.array(a)
A

  • We can use the attribute ndim to obtain the number of axes or dimensions referred to as the rank. 


    • 
# Show the numpy array dimensions

A.ndim

  • Attribute shape returns a tuple corresponding to the size or number of each dimension. 


    • 
# Show the numpy array shape

A.shape

  • The total number of elements in the array is given by the attribute size. 


    • 
# Show the numpy array size

A.size

  • Accessing different elements of a Numpy Array We can use rectangular brackets to access the different elements of the array. The correspondence between the rectangular brackets and the list and the rectangular representation is shown in the following figure for a 3x3 array:


  • Access the element on the second row and third column


  • We can access the 2nd-row 3rd column as shown in the following figure:


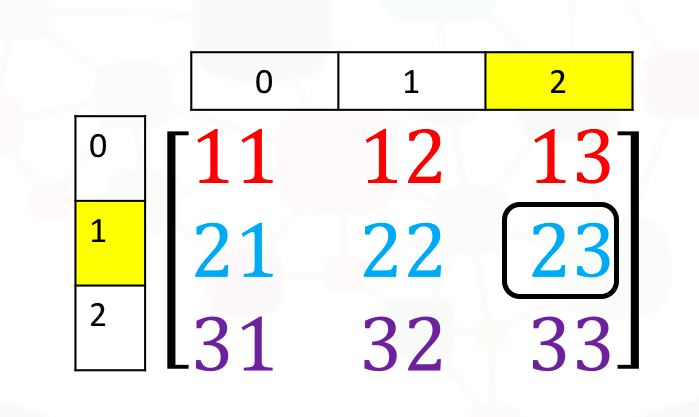
  • Access the element on the second row and third column


  • We simply use the square brackets and the indices corresponding to the element we would like: 


    • 
# Access the element on the second row and third column

A[1, 2]

  • We can also use the following notation to obtain the elements: 


    • 
# Access the element on the second row and third column

A[1][2]

  • Consider the elements shown in the following figure


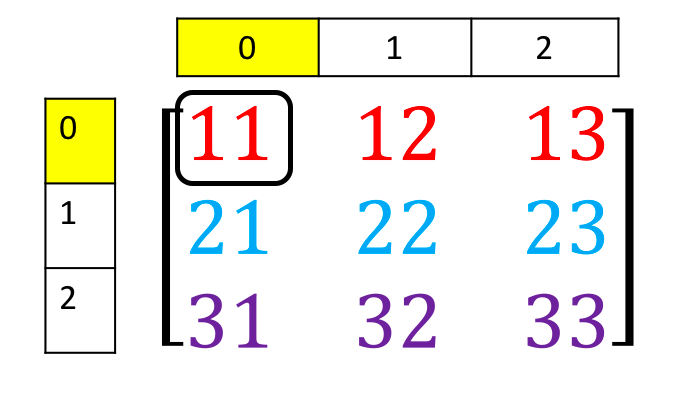
  • Access the element on the second row and third column


  • We can access the element as follows 


    • 
# Access the element on the first row and first column

A[0][0]

  • We can also use slicing in numpy arrays. Consider the following figure. We would like to obtain the first two columns in the first row


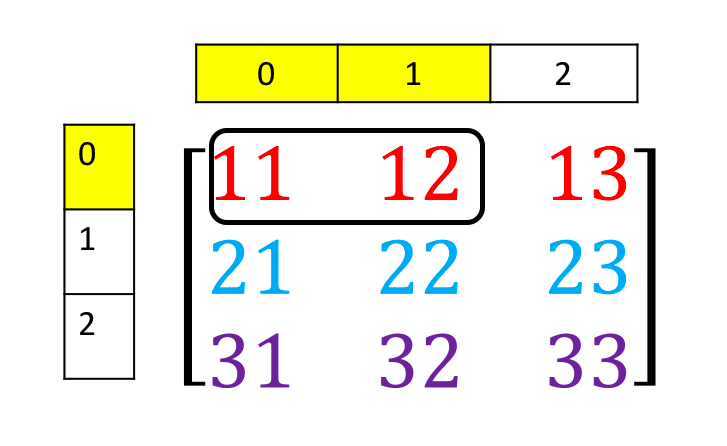
  • slicing in numpy arrays


  • This can be done with the following syntax 


    • 
# Access the element on the first row and first and second columns

A[0][0:2]

  • Similarly, we can obtain the first two rows of the 3rd column as follows: 


    • 
# Access the element on the first and second rows and third column

A[0:2, 2]

  • Corresponding to the following figure:


  • Access the element on the first and second rows and third column


  • Basic Operations We can also add arrays. The process is identical to matrix addition. Matrix addition of X and Y is shown in the following figure:


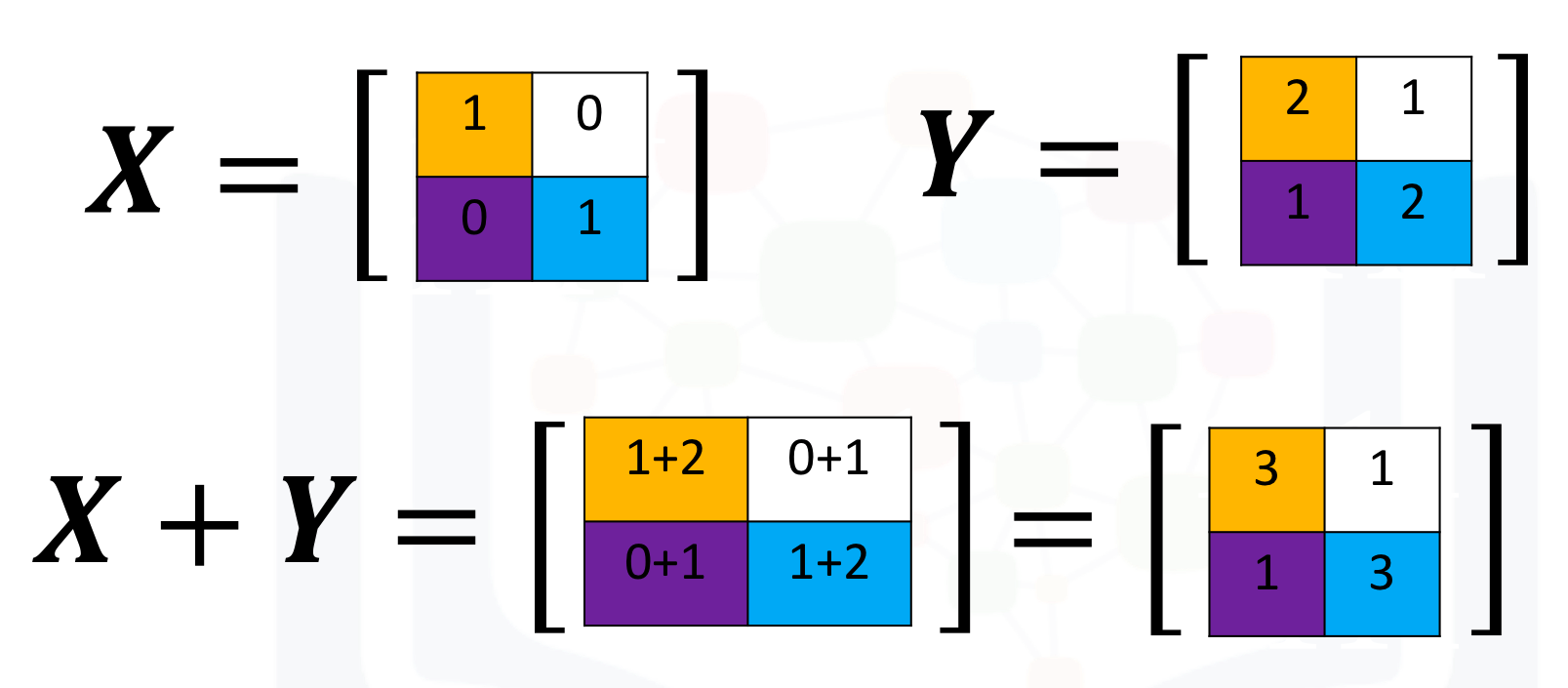
  • add arrays in python


  • The numpy array is given by X and Y 


    • 
# Create a numpy array X

X = np.array([[1, 0], [0, 1]]) 
X
 

    
# Create a numpy array Y

Y = np.array([[2, 1], [1, 2]]) 
Y

  • We can add the numpy arrays as follows. 


    • 
# Add X and Y

Z = X + Y
Z

  • Multiplying a numpy array by a scaler is identical to multiplying a matrix by a scaler. If we multiply the matrix Y by the scaler 2, we simply multiply every element in the matrix by 2 as shown in the figure.


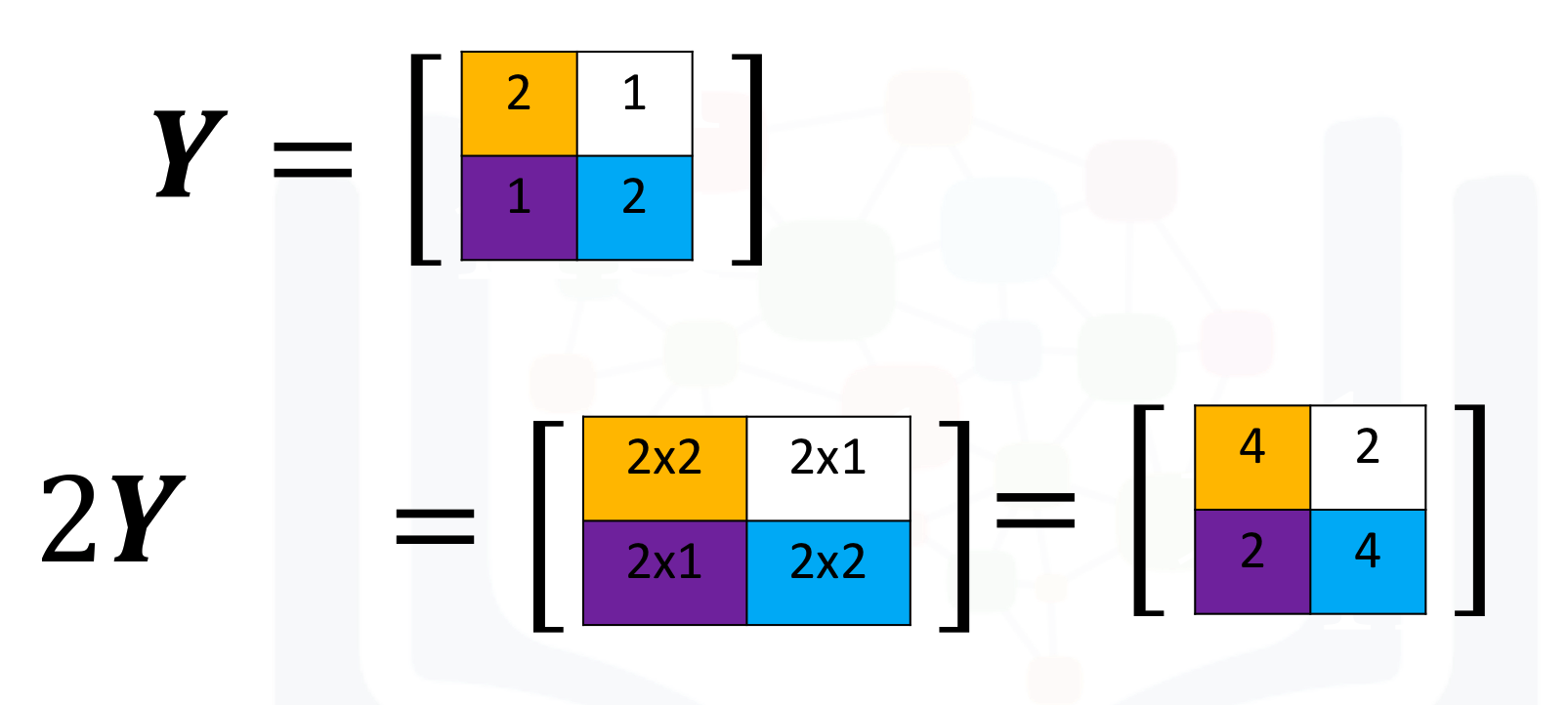
  • Multiplying a numpy array by a scaler


  • We can perform the same operation in numpy as follows 


    • 
# Create a numpy array Y

Y = np.array([[2, 1], [1, 2]]) 
Y
 

    
# Multiply Y with 2

Z = 2 * Y
Z

  • Multiplication of two arrays corresponds to an element-wise product or Hadamard product. Consider matrix X and Y.


  • The Hadamard product corresponds to multiplying each of the elements in the same position, i.e. multiplying elements contained in the same color boxes together.


  • The result is a new matrix that is the same size as matrix Y or X, as shown in the following figure.


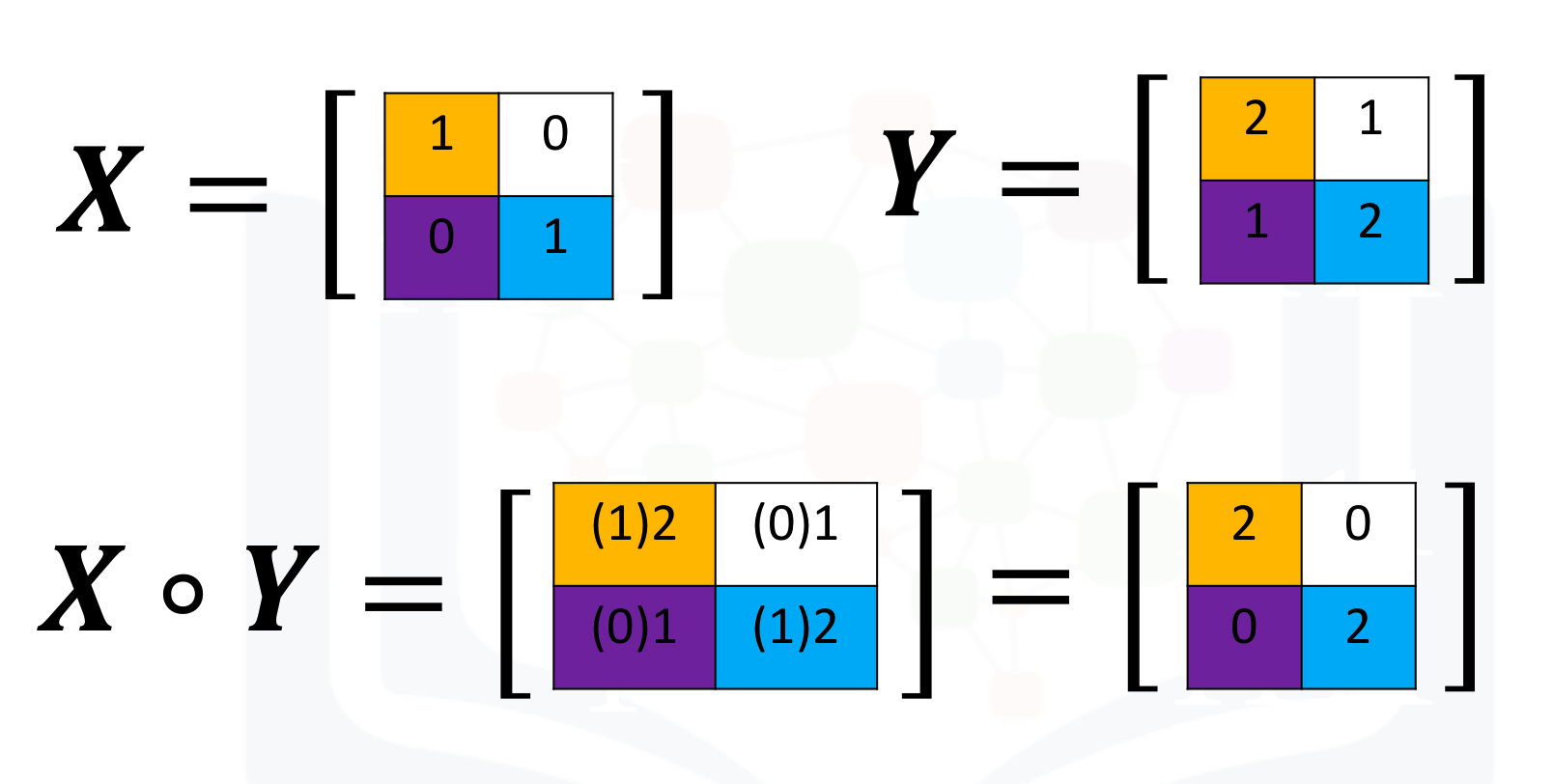
  • Multiplication of two arrays pandas


  • We can perform element-wise product of the array X and Y as follows: 


    • 
# Create a numpy array Y

Y = np.array([[2, 1], [1, 2]]) 
Y
 

    
# Create a numpy array X

X = np.array([[1, 0], [0, 1]]) 
X
 

    
# Multiply X with Y

Z = X * Y
Z

  • We can also perform matrix multiplication with the numpy arrays A and B as follows:


  • First, we define matrix A and B: 


    • 
# Create a matrix A

A = np.array([[0, 1, 1], [1, 0, 1]])
A


# Create a matrix B

B = np.array([[1, 1], [1, 1], [-1, 1]])
B

  • We use the numpy function dot to multiply the arrays together. 


    • 
# Calculate the dot product

Z = np.dot(A,B)
Z


# Calculate the sine of Z

np.sin(Z)

  • We use the numpy attribute T to calculate the transposed matrix 


    • 
# Create a matrix C

C = np.array([[1,1],[2,2],[3,3]])
C
# Get the transposed of C

C.T