CAT 2001

1. A student took five papers in an examination, where the full marks were the same for each paper.
His marks in these papers were in the proportion of 6 : 7 : 8 : 9 : 10. In all papers together, the candidate obtained 60% of the total marks. Then the number of papers in which he got more than 50% marks is

(a) 2

(b) 3

(d) 5

Ans .

Explanation :
Let the marks scored in five subjects be 6x, 7x, 8x, 9x and 10x (on a scale of 1). Average score = 60% ⇒\(\frac{6x+7x+8x+9x+10x}{5}\)= \( \frac{60}{100} \)⇒ 8x = 0.6 ⇒ x = 0.075
So the marks are 0.45, 0.525, 0.6, 0.675 and 0.75. Number of times the marks exceed 50% is 4.

2. A square, whose side is 2 m, has its corners cut away so as to form an octagon with all sides equal.
Then the length of each side of the octagon, in metres, is

(a) \( \frac{√2}{√2+1} \)

(b) \( \frac{2}{√2+1} \)

(d) \( \frac{√2}{√2-1} \)

Ans .

(b)

Explanation :

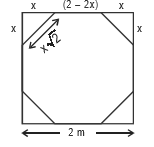
Let the length of the edge cut at each corner be x m. Since the resulting figure is a regular octagon,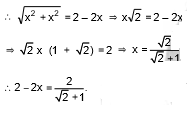

3. Let x, y and z be distinct integers. x and y are odd and positive, and z is even and positive.
Which one of the following statements cannot be true?

(a) y(x – z)2 is even

(b) y2(x – z) is odd

(d)z(x – y)2 is even

Ans .

(a)

Explanation :
Check the answer choices basis the fact that: Odd × Odd = Odd Odd × Even = Even Even × Even = Even

4. If x > 5 and y < –1, then which of the following statements is true?

(a) (x + 4y) > 1

(b) x > –4y

(d) None of these

Ans .

(d)

Explanation :
x > 5, y < –1 Use answer choices. Take x = 6, y = –6. We see none of the statements (a), (b) and (c) is true.
Hence the correct option is (d).

5. A red light flashes three times per minute and a green light flashes five times in 2 min at regular intervals.
If both lights start flashing at the same time, how many times do they flash together in each hour?

(a)30

(b)24

(d) 60

Ans .

(a)

Explanation :
First light blinks after 20 s. Second light blinks after 24 s.
They blink together after LCM (20 and 24) = 120 s = 2 min. Hence, the number of times they blink together in an hour = 30

6. Of 128 boxes of oranges, each box contains at least 120 and at most 144 oranges. The number of boxes containing the same number of oranges is at least

(a)5

(b)103

(d) cannot be determine

Ans .

(c)

Explanation :
We can put a minimum of 120 oranges and a maximum of 144 oranges, i.e., 25 oranges need to be filled in 128 boxes. There are 25 different possibilities if there are 26 boxes.
In such a case, at least 2 boxes contain the same number of oranges. (i.e., even if each of the 25 boxes contain a different number of oranges, the 26th must contain one of these numbers).
Similarly, if there are 51 boxes, at least 3 boxes contain the same number of oranges. Hence, at least 6 boxes have the same number of oranges in case of 128 boxes.

7. A certain city has a circular wall around it, and this wall has four gates pointing north, south, east and west. A house stands outside the city, 3 km north of the north gate,
and it can just be seen from a point 9 km east of the south gate. What is the diameter of the wall that surrounds the city?

(a)6km

(b)9km

(d)none of these

Ans .

(b)

Explanation :

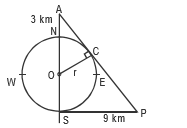
∆APS and ∆AOC are similar triangles. Where OC = r
\( \frac{r}{r+3} \) = \( \frac{9}{√(81 (2r+3)2} \)
Now use the options. Hence, the diameter is 9 km.

8.
In the above diagram, ABCD is a rectangle with AE = EF = FB. What is the ratio of the areas of ∆CEF and that of the rectangle?

(a) \( \frac{1}{6} \)

(b)\( \frac{1}{8} \)

(c)\( \frac{1}{9} \)
(d)none of these

Ans .
(a)

Explanation :
Let BC = y and AB = x. Then area of ∆CEF = Area(∆CEB) – Area(∆CFB)
\( \frac{1}{2} \).\( \frac{2x}{3} \).y-\( \frac{1}{9} \).\( \frac{x}{3} \).y=\( \frac{xy}{6} \)

\( \frac{xy}{6} \):xy = \( \frac{1}{6} \)
Alternate method: Join AC, therefore Area of
∆ABC=\( \frac{1}{2} \)Area of ABCD Also, Area of ∆CAE= Area of ∆CEF= Area of ∆CFB Area of ∆CEF Area of ABCD 1/6

9. A can complete a piece of work in 4 days. B takes double the time taken by A, C takes double that of B, and D takes double that of C to complete the same task. They are paired in groups of two each.
One pair takes two-thirds the time needed by the second pair to complete the work. Which is the first pair?

(a)A and B

(b)A and C

(c) B and C
(d) A and D

Ans .
(d)

Explanation :
Work done in one day by A, B, C and D are
\( \frac{1}{4} \),\( \frac{1}{8} \),\( \frac{1}{16} \) and \( \frac{1}{32} \)
respectively. Using answer choices, we note that the pair of B and C does \( \frac{3}{16} \) of work in one day; the pair of A and D does \( \frac{1}{4} \)+\( \frac{1}{32} \)=\( \frac{9}{32} \)of the work in one day. Hence, A and D take 32/9 days B and C take = days.\( \frac{166}{3} \)=\( \frac{32}{6} \)days Hence, the first pair must comprise of A and D.

10. In a four-digit number, the sum of the first 2 digits is equal to that of the last 2 digits. The sum of the first and last digits is equal to the third digit.
Finally, the sum of the second and fourth digits is twice the sum of the other 2 digits. What is the third digit of the number?

(a) 5

(b) 8

(c) 1
(d) 4

Ans .
(a)

Explanation :
Let the four-digit number be abcd.
a + b = c + d ... (i)

b + d = 2(a + c) ... (ii)

a + d = c ... (iii)
From (i) and (iii), b = 2d

From (i) and (ii),

3b = 4c + d
⇒ 3(2d) = 4c + d ⇒ 5d = 4c
⇒ d 4 5 c = Now d can be 4 or 8. But if d = 8, then c = 10 not possible. So d = 4 which gives c = 5.

11.Two men X and Y started working for a certain company at similar jobs on January 1, 1950. X asked for an initial salary of Rs. 300 with an annual increment of Rs. 30. Y asked for
an initial salary of Rs. 200 with a rise of Rs. 15 every 6 months. Assume that the arrangements remained unaltered till December 31, 1959. Salary is paid on the last day of the month. What is the total amount paid to them as salary during the period?

(a) Rs. 93,300

(b) Rs. 93,200

(c) Rs. 93,100
(d) none of these

Ans .
(a)

Explanation :
Amount of money given to X
= 12 × 300 + 12 × 330 + ... + 12 × 570

= 12[300 + 330 + ... + 540 + 570]

12×10/2[600 + 9 × 30]= 52200

Amount of money given to Y is

6 × 200 + 6 × 215 + 6 × 230 + 6 × 245 + ... to 20 terms
]1519400[ 2 20 6 × = 6 × 10[400 + 285] = 60 × 685 = 41100 ∴Total amount paid = 52200 + 41100 = Rs. 93,300

12.Anita had to do a multiplication. Instead of taking 35 as one of the multipliers, she took 53. As a result, the product went up by 540. What is the new product?

(a)1050

(b)540

(c)1440
(d)1590

Ans .
(d)

Explanation :
Let the number be x. Increase in product = 53x – 35x = 18x⇒ 18x = 540 ⇒ x = 30 Hence new product = 53 × 30 = 1590.

13.A college has raised 75% of the amount it needs for a new building by receiving an average donation of Rs. 600 from the people already solicited.
The people already solicited represent 60% of the people the college will ask for donations. If the college is to raise exactly the amount needed for the new building, what should be the average donation from the remaining people to be solicited?

(a) Rs. 300

(b) Rs. 2550

(c) Rs. 400
(d) Rs. 500

Ans .
(a)

Explanation :
Let x be the total number of people the college will ask for donations.
∴People already solicited = 0.6x Amount raised from the people solicited = 600 × 0.6x = 360x Now 360x constitutes 75% of the amount. Hence, remaining 25% = 120x Hence, average donation from remaining people =120x/0.4x=Rs300

14. x and y are real numbers satisfying the conditions 2 < x < 3 and – 8 < y < –7. Which of the following expressions will have the least value?

(a) Rs. 300

(b) Rs. 2550

(c) Rs. 400
(d) Rs. 500

Ans .
(c)

Explanation :
The value of y would be negative and the value of x would be positive from the inequalities given in the question. Therefore, from (b) and (d), y becomes positive.
The value of xy2 would be positive and will not be the minimum. From (a) and (c), x2y and 5xy would give negative values but we do not know which would be the minimum. On comparing (a) and (c), we find that x2 < 5x in 2 < x < 3. 2 x y 5xy ∴> [Since y is negative.] ∴ 5xy would give the minimum value.

15.m is the smallest positive integer such that for any integer m n ≥ , the quantity n3 – 7n2 + 11n – 5 is positive. What is the value of m?

(a)4

(b)5

(c)8
(d)none of these

Ans .
(d)

Explanation :

Let y = n3 – 7n2 + 11n – 5 At n = 1, y = 0 ∴(n – 1) (n2 – 6n + 5) = (n – 1)2 (n – 5) Now (n – 1)2 is always positive. For n < 5, the expression gives a negative quantity. Therefore, the least value of n will be 6. Hence, m = 6.

16.A ladder leans against a vertical wall. The top of the ladder is 8 m above the ground. When the bottom of the ladder is moved 2 m farther away from the wall, the top of the ladder rests against the foot of the wall. What is the length of the ladder?

(a) 10m

(b) 15m

(c)20m
(d)17m

Ans .
(d)

Explanation :

Let the length of the ladder be x meter. We have 82 + y2 = x2 and (y + 2) = x Hence, 64 + (x – 2)2 = x2 ⇒ 64 + x2 – 4x + 4 = x2 ⇒ 68 = 4x ⇒ x = 17

17.Three friends, returning from a movie, stopped to eat at a restaurant. After dinner, they paid their bill and noticed a bowl of mints at the front counter.
Sita took one-third of the mints, but returned four because she had a momentary pang of guilt. Fatima then took one-fourth of what was left but returned three for similar reason. Eswari then took half of the remainder but threw two back into the bowl. The bowl had only 17 mints left when the raid was over. How many mints were originally in the bowl?

(a) 38

(b) 31

(c) 41
(d) none of these

Ans .
(d)

Explanation :
Let there be x mints originally in the bowl. Sita took 1/3 , but returned 4. So now the bowl has 4 x 2/3 + mints. Fatima took 1/4 of the remainder, but returned 3. So the bowl now has \( \frac{3}{4} \)\( \frac{2}{3}× +4 \)+ mints Eshwari took half of remainder that is

Short cut: Since Sita was the first person to pick and she picks up 1 3 of the mint, but if you see the options, none of the option is a multiple of 3.

18.If 09/12/2001(DD/MM/YYYY) happens to be Sunday, then 09/12/1971 would have been a

(a) wednesday

(b) tuesday

(c) saturday
(d) thursday

Ans .

Explanation :
In 30 years from 1971 to 2001, number of odd days = 30 + (8 from leap years) = 38 and 38 ≡ 3 mod 7 So December 9, 1971 is Sunday – 3 days = Thursday

19.In a number system, the product of 44 and 11 is 3414. The number 3111 of this system, when converted to the decimal number system, becomes

(a) 406

(b) 1086

(c)213
(d)691

Ans .
(a)

Explanation :

This equation is satisfied only when x = 5. So base is 5. In decimal system, the number 3111 can be written as 406.

20.At his usual rowing rate, Rahul can travel 12 miles downstream in a certain river in 6 hr less than it takes him to travel the same distance upstream. But if he could double his usual rowing rate for this 24 miles round trip, the downstream 12 miles would then take only 1 hr less than the upstream 12 miles. What is the speed of the current in miles per hour?

(a)\( \frac{7}{2} \)

(b) \( \frac{4}{3} \)

(c)\( \frac{5}{3} \)
(d)\( \frac{8}{3} \)

Ans .
(d)

Explanation :
Let x be the speed of Rahul, and y be the speed of current in mph.

21.Every 10 years the Indian Government counts all the people living in the country. Suppose that the director of the census has reported the following data on two neighbouring villages Chota Hazri and Mota Hazri. Chota Hazri has 4,522 fewer males than Mota Hazri. Mota Hazri has 4,020 more females than males. Chota Hazri has twice as many females as males. Chota Hazri has 2,910 fewer females than Mota Hazri. What is the total number of males in Chota Hazri? .

(a) 11,264

(b)14,174

(c) 5,632
(d)10,154

Ans .
(c)

Explanation :
Let ‘x’ be the number of males in Mota Hazri. Chota Hazri Mota Hazri Males x – 4522 x Females 2(x – 4522) x + 4020 x + 4020 – 2(x – 4522) = 2910 ⇒ x = 10154 ∴Number of males in Chota Hazri = 10154 – 4522 = 5632

22.Three classes X, Y and Z take an algebra test. The average score in class X is 83. The average score in class Y is 76. The average score in class Z is 85. The average score of all students in classes X and Y together is 79. The average score of all students in classes Y and Z together is 81.What is the average for all the three classes?

(a) 81

(b) 81.5

(c) 82
(d)84.5

Ans .
(b)

Explanation :
Let the number of students in classes X, Y and Z be a, b and c respectively. Then, total of X = 83a total of Y = 76b total of Z = 85c

23.Two sides of a plot measure 32 m and 24 m and the angle between them is a perfect right angle. The other two sides measure 25 m each and the other three angles are not right angles.
What is the area of the plot?

(a) 768 m^2

(b) 534 m^2

(c) 696.5 m^2
(d) 684 m^2

Ans .
(d)

Explanation :
CE = 22 25 – 20 = 15 (Since DBC is isosceles triangle.) ABCD is a quadrilateral where AB = 32 m, AD = 24 m, DC = 25 m, CB = 25 m
and DAB ∠ is right angle. By Pythagoras Theorem: DB = 40 m So area of ∆ADB=1/2×32× 24 ×384 sq.m.Now in isosceles ∆ BCD, perpendicular CE from C to BD bisects BD. BE = DE = 40/2 Now by Pythagoras Theorem: CE = √(25^2-20)^2 = 15m So area of ∆BCD = 2×11/2 ×15 ×20 =300sq.m Hence, area of ABCD = 384 + 300 = 684 sq. m

24. All the page numbers from a book are added, beginning at page 1. However, one page number was added twice by mistake. The sum obtained was 1000. Which page number was added twice?

(a)44

(b)45

(c)10
(d)12

Ans .
(b)

Explanation :
Let the total number of pages in the book be n. Let page number x be repeated

25. Shyama and Vyom walk up an escalator (moving stairway). The escalator moves at a constant speed. Shyama takes three steps for every two of Vyom’s steps. Shyama gets to the top of the escalator after having taken 25 steps, while Vyom (because his slower pace lets the escalator do a little more of the work) takes only 20 steps to reach the top. If the escalator were turned off, how many steps would they have to take to walk up?

(a)40

(b)50

(c)60
(d)80

Ans .
(b)

Explanation :
If Shyam takes 1 min for every 3 steps, then he takes 3 1 min for every step. For 25 steps, he takes 3/ 25 min, i.e. 8.33 min. So Vyom takes 2/ 1 min for every step. For 20 steps, he takes 2 20 min, i.e. 10 min. Difference between their time = 1.66 min.
Escalator takes 5 steps in 1.66 min and difference in number of steps covered = 5 Speed of escalator is 1 step for 0.33 min, i.e. 3 steps per minute. If escalator is moving, then Shyam takes 25 steps and escalator also takes 25 steps. Hence, total number of steps = 50.

26. At a certain fast food restaurant, Brian can buy 3 burgers, 7 shakes, and one order of fries for Rs. 120 exactly. At the same place it would cost Rs. 164.50 for 4 burgers, 10 shakes, and one order of fries. How much would it cost for an ordinary meal of one burger, one shake, and one order of fries?

(a) Rs. 31

(b) Rs. 41

(c) Rs. 21
(d) none of these

Ans .
(a)

Explanation :
Let the cost of 1 burger, 1 shake and 1 fries be x, y and z. Then,
3x + 7y + z = 120 ...(i)
4x + 10y + z = 164.50 ...(ii)
On performing: (i) × 3 – (ii) × 2,
we get, x + y + z = 31.

27.If a, b, c and d are four positive real numbers such that abcd = 1, what is the minimum value of (1 + a)(1 + b)(1 + c)(1 + d)?

(a) 4

(b) 1

(c)16
(d) 18

Ans .
(c)

Explanation :
Taking a = b = c = d = 1, we get the minimum value as (1 + 1) (1 + 1) (1 + 1) (1 + 1) = 2 × 2 × 2 × 2 = 16.

28.There’s a lot of work in preparing a birthday dinner. Even after the turkey is in the oven, there’s still the potatoes and gravy, yams, salad, and cranberries, not to mention setting the table. Three friends — Asit, Arnold and Afzal — work together to get all of these chores done. The time it takes them to do the work together is 6 hr less than Asit would have taken working alone, 1 hr less than Arnold would have taken alone, and half the time Afzal would have taken working alone. How long did it take them to do these chores working together?

(a) 20 min

(b) 30 min

(c) 40 min
(d) 50 min

Ans .
(c)

Explanation :
Let ‘t’ be the time taken for all three together, then
\( \frac{1}{t+6} \)+\( \frac{1}{t+1} \)+\( \frac{1}{2t} \)=\( \frac{1}{t} \)

29.Euclid has a triangle in mind. Its longest side has length 20 and another of its sides has length 10. Its area is 80. What is the exact length of its third side?

(a) 260

(b) 250

(c) 240
(d)270

Ans .
(c)

Explanation :

30.For a Fibonacci sequence, from the third term onwards, each term in the sequence is the sum of the previous two terms in that sequence. If the difference in squares of 7th and 6th terms of this sequence is 517, what is the 10th term of this sequence?

(a) 147

(b) 76

(c) 123
(d) cannot be determine

Ans .
(c)

Explanation :
Let the 6th and the 7th terms be x and y. Then 8th term = x + y Also y2 – x2 = 517 ⇒ (y + x)(y – x) = 517 = 47 × 11 So y + x = 47 y – x = 11
Taking y = 29 and x = 18, we have 8th term = 47, 9th term = 47 + 29 = 76 and 10th term = 76 + 47 = 123

31.Fresh grapes contain 90% water by weight while dried grapes contain 20% water by weight. What is the weight of dry grapes availabel from 20 kg of fresh grapes?

(a) 2 kg

(b) 2.4 kg

(c) 2.5 kg
(d) none of these

Ans .
(c)

Explanation :
Fresh grapes contain 10% pulp. ∴20 kg fresh grapes contain 2 kg pulp. Dry grapes contain 80% pulp.
∴ 2 kg pulp will contain \( \frac{2}{0.8} \)= \( \frac{20}{8} \)= 2.5 kg kg drygrapes.

32.Train X departs from station A at 11 a.m. for station B, which is 180 km so far. Train Y departs from station B at 11 a.m. for station A. Train X travels at an average speed of 70 km/hr and does not stop anywhere until it arrives at station B. Train Y travels at an average speed of 50 km/hr, but has to stop for 15 min at station C, which is 60 km away from station B enroute to station A. Ignoring the lengths of the trains, what is the distance, to the nearest kilometre, from station A to the point where the trains cross each other?

(a) 112 km

(b) 118 km

(c) 120 km
(d) none of these

Ans .
(a)

Explanation :
Total time taken by B to cover 60 km \( \frac{60}{50} \)hr = \( \frac{6}{5} \)It stops at station C for\( \frac{1}{4} \)hr Now, in \( \frac{6}{5} \)+\( \frac{1}{4} \)hr train X travels 70 × \( \frac{29}{20} \)=101.5 km This implies that they do not cross each other by the time train Y finishes its stoppage at station C. Let they meet after t hr. Then 70t + 50(t – 4 1) = 180 120/ 5.192 t =⇒ hr Distance from A will be (70 × 120 ×5.192) km = 112 km approximately

33.A set of consecutive positive integers beginning with 1 is written on the blackboard. A student came along and erased one number. The average of the remaining numbers is 35 7/17 . What was the number erased?

(a) 7

(b) 8

(c) 9
(d) none of these

Ans .
(a)

Explanation :
Let the highest number be n and x be the number erased.

34.In DDEF shown below, points A, B and C are taken on DE, DF and EF respectively such that EC = AC and CF = BC. If D 40 ∠ = °, then ∠ ACB

(a)140°

(b) 70°

(c)100°
(d) none of these

Ans .
(c)

Explanation :
Let ∠AEC x and ∠ BFC = y

Here ∠ACE=180° – 2x , ∠BCF = 180° – 2y and x + y + 40° = 180° (In ∆DEF) So x + y = 140°

So ∠ACB = 180° – ∠ACE – ∠BCF = 180° – (180° – 2x) – (180° – 2y) = 2(x + y) – 180° = 2 × 140° – 180° = 100°.

35.The owner of an art shop conducts his business in the following manner: every once in a while he raises his prices by X%, then a while later he reduces all the new prices by X%. After one such updown cycle, the price of a painting decreased by Rs. 441. After a second up-down cycle the painting was sold for Rs. 1,944.81. What was the original price of the painting?

(a) Rs. 2,756.25

(b) Rs. 2,256.25

(c) Rs. 2,500
(d) Rs. 2,000

Ans .
(a)

Explanation :
In first updown cycle, the reduction price is Rs. 441. According to this, (b) and (d) are removed. Now we have to analyse (c), if the original price is Rs. 2,500, then after first operation, the price will be 2500 – 441= Rs. 2,059. In second operation, it will come down to around Rs. 168 [here decrease% = 441/2500 x 100 = 18%] So the value is not equivalent to Rs. 1,944.81. Hence, option (a) is the answer.

36.Three runners A, B and C run a race, with runner A finishing 12 m ahead of runner B and 18 m ahead of runner C, while runner B finishes 8 m ahead of runner C. Each runner travels the entire distance at a constant speed. What was the length of the race?

(a) 36m

(b) 48m

(c) 60m
(d) 72m

Ans .
(b)

Explanation :
Let L be length in metres of the race which A finishes in t seconds

37.

(a) 12

(b) 20

(c) 12.5
(d) 13.3

Ans .
(c)

Explanation :
Let L be length in metres of the race which A finishes in t seconds

38.Based on the above information which of the following is true?

(a)MBA1≤ BA≤ MBA2

(b) MA≤ MBA2≤ MBA1

(c) MBA2≤ BA≤ MBA1
(d) none of these

Ans .
(d)

Explanation:
From the above information, 12 BA MBA MBA ≥≥ None of these is the right answer

39.An experienced cricketer with no incomplete innings has BA of 50. The next time he bats, the innings is incomplete and he scores 45 runs. It can be inferred that

(a) BA and MBA1 will both increase

(b) BA will increase and MBA2 will decrease

(c) BA will increase and not enough data is availabel to assess change in MBA1 and MBA2
(d) none of these

Ans .
(b)

Explanation:

40.Based on the figure below, what is the value of x, if y = 10?

(a) 10

(b) 11

(c) 12
(d) none of these

Ans .
(b)

Explanation:

41.A rectangular pool 20 m wide and 60 m long is surrounded by a walkway of uniform width. If the total area of the walkway is 2 516 m , how wide, in metres, is the walkway?

(a) 43 m

(b) 4.3m

(c) 3m
(d) 3.5m

Ans .
(c)

Explanation:

Let width of the path be x metres. ∴(60 + 2x)(20 + 2x) – 60 × 20 = 516 ⇒ 1200 + 120x + 40x + 4x2 – 1200 = 516 ⇒ 4x2 + 160x – 516 = 0 ⇒ x2 + 40x – 129 = 0 ⇒ x = 3 or –43 (not acceptable)

42. Let b be a positive integer and a = b2 – b. If 4 b ≥ , then a2 – 2a is divisible by

(a) 15

(b) 20

(c) 24
(d) all of these

Ans .
(d)

Explanation:
a = b2 – b, b ≥ 4 a2 – 2a = (b2 – b)2 – 2(b2 – b) = (b – 2)(b – 1) b (b + 1) Using different values of b ≥ 4, we will find that a2 – 2a is divisible by 15, 20 and 24. Hence, all of these is the right answer.

43. Ashish is given Rs. 158 in one-rupee denominations. He has been asked to allocate them into a number of bags such that any amount required between Re 1 and Rs. 158 can be given by handing out a certain number of bags without opening them. What is the minimum number of bags required?

(a)11

(b) 12

(c)13
(d) none of these

Ans .
(d)

Explanation:
Number of one-rupee coins = 158. Possible arrangements of coins are listed as 1, 2, 4, 8, 16, 32, 64 and 31. ∴Number of arrangements = 8. So the least number of bags required = 8.

44.In some code, letters a, b, c, d and e represent numbers 2, 4, 5, 6 and 10. We just do not know which letter represents which number. Consider the following relationships: I. a + c = e, II. b – d = d and III. e + a = b Which of the following statements is true?

(a) b = 4, d = 2

(b) a = 4, e = 6

(c) b = 6, e = 2
(d) a = 4, c = 6

Ans .
(b)

Explanation:
From II, b = 2d Hence, b = 10, d = 5 or b = 4, d = 2 From III, e + a = 10 or e + a = 4
From I, a + c = e or e – a = c From III and I, we get 2e = 10 + c or 2e = 4 + c ⇒ce52 =+ ... (i) or ce2 2 =+ ... (ii) From (i),
we can take c = 2, 4, 6, 10. For c = 2, e = 6 c = 4, e = 7 (Not possible) c = 6, c = 8 (Not possible) c = 10, e = 10 (Not possible since both c and e cannot be 10) From (ii),
we have c = 2, 4, 6, 10. For c = 2, e = 3 (Not possible) c = 4, e = 4 (Not possible) c = 6, e = 5 (Possible) c = 10, e = 7 (Not possible) Considering the possibility from B that c = 6 and e = 5 means e + a = 4 ⇒ a = –1 (Not possible) Hence, only possibility is b = 10, d = 5, c = 2, e = 6. e + a = 10 ⇒ a = 4

45.Ujakar and Keshab attempted to solve a quadratic equation. Ujakar made a mistake in writing down the constant term. He ended up with the roots (4, 3). Keshab made a mistake in writing down the coefficient of x. He got the roots as (3, 2). What will be the exact roots of the original quadratic equation?

(a) (6, 1)

(b) (–3, –4)

(c) (4, 3)
(d) (–4, –3)

Ans .
(a)

Explanation:
Quadratic equation having roots (4, 3) is (x – 4) (x – 3) = 0 ⇒ x2 – 7x + 12 = 0 ... (i)
Quadratic equation having roots (3, 2) is (x – 3) (x – 2) = 0 ⇒ x2 – 5x + 6 = 0 ... (ii)
Picking the coefficient of x from (i)
and the constant term from (ii),
we get the required equation x2 – 7x + 6 = 0 ⇒ (x – 6) (x – 1) = 0 ∴x = 1, 6 Hence, actual roots are (6,1). Alternate method: Since constant = [3 × 2] and coefficient of x = [–4x – 3x] = –7 Since quadratic equation is x2 – (Sum of roots)x + Product of roots = 0 or x2 – 7x + 6 = 0 Solving the equation, (x – 6)(x – 1) = 0 or x = (6, 1).

46.A change-making machine contains one-rupee, two-rupee and five-rupee coins. The total number of coins is 300. The amount is Rs. 960. If the numbers of one-rupee coins and two-rupee coins are interchanged, the value comes down by Rs. 40. The total number of five-rupee coins is

(a)100

(b)140

(c)60
(d) 150

Ans .
(b)

Explanation:
Let the number of five-rupee, two-rupee and onerupee coins be x, y and z respectively.
x + y + z = 300 ...(i)
5x + 2y + z = 960 ...(ii)
5x + y + 2z = 920 ...(iii) (i) – (ii):
y –z = 40 ...(iv)
5 × (i) – (ii):
3y + 4z = 540 ...(v) Solving (iv) and (v), we get, y = 100 and z = 60. Hence, the number of coins = 300 – (100 + 60) = 140

47.The figure below shows the network connecting cities A, B, C, D, E and F. The arrows indicate permissible direction of travel. What is the number of distinct paths from A to F?

(a)9

(b) 10

(c)11
(d) none of these

Ans .
(b)

Explanation:

48.Let n be the number of different five-digit numbers, divisible by 4 with the digits 1, 2, 3, 4, 5 and 6, no digit being repeated in the numbers. What is the value of n? .

(a)144

(b) 168

(c)192
(d) none of these

Ans .
(c)

Explanation:
The last two digits can be 12, 16, 24, 32, 36, 52, 56, and 64, i.e. 8 possibilities Remaining digits can be chosen in 24 P34 = ways. Hence, total number of such five-digit numbers = 24 × 8 = 192.

49. Manasa makes a 200 km trip from Mumbai to Pune at a steady speed of 60 km/hr. What is the volume of petrol consumed for the journey?

(a) 12.5 L

(b) 13.33 L

(c)16 L
(d) 19.75 L

Ans .
(b)

Explanation:

60 km/hr is travelled in 4 L petrol (from the graph). ∴1 L is required for 15 km, i.e. for 15 km, 1 L petrol is required. For 200 km, 200/15
= 13.33 L is required.

50. Manasa would like to minimize the fuel consumption for the trip by driving at the appropriate speed. How should she change the speed?

(a) Increase the speed

(b)) Decrease the speed

(c) Maintain the speed at 60 km/hr
(d) cannot e determined

Ans .
(b)

Explanation:
The fuel consumption at various speeds would be \( \frac{200}{40} \)× 2.5 = 12.5L
\( \frac{200}{80} \)× 2.5 = 19.75L
\( \frac{200}{60} \)× 2.5 = 13.33 LIf Manasa travels at 40 km/hr, the total consumption would be 12.5 L. Hence Manasa has to decrease the speed.

51.

(a)

(b)

(c)
(d)

Ans .
(c)

Explanation:
A–H: Here ‘exceed’ would mean ‘flowing beyond’ the ‘banks’ (physical boundaries).
B–F: Here their accomplishments ‘were superior to’ the expectation.
C–E: It is difficult for us to ‘comprehend’ the infinite mercy of God.
D–G: He ‘crossed limits’ when he embezzled from the fund.

52.

(a)

(b)

(c)
(d)

Ans .
(d)

Explanation:
A–E: We see smoke and ‘deduce’ that there must be a fire.
B–F: The listener makes all sorts of guesses about the ‘utterance’.
C–G: ‘You’ can be sure from ‘the long wait’ that the person is definitely inclined to meet ‘him’.
D–H: She had distanced herself from the debate but for a perfunctory question, thereby ‘hinting’ that she was not exactly excited by the debate.

53.

(a)

(b)

(c)
(d)

Ans .
(c)

Explanation:
A–G: The wines have been preserved for a long time so as to ‘age’ it.
B–E: He has been “freed from the rashness of youth” in his old age.
C–H: The soil in the Gangetic plains are ‘rich’ with the flow of time.
D–F: The violin tunes were ‘rich and pleasant’

54.

(a)

(b)

(c)
(d)

Ans .
(b)

Explanation:
A–F: The author felt “light after removing something distressing ‘shoes’
B–H: The victims were given relief ‘aid’.
C–G: The only ‘diversion’ I get is by playing cards.
D–E: The sentry was ‘released from the performance of duty’

55.

(a)

(b)

(c)
(d)

Ans .
(d)

Explanation:
A–F: The committee heard his attempt to “remove the stigma” from his name.
B–H: Water had to be purified of “foreign/superfluous” ingredients by distillation.
C–E: The opposition was “gotten rid of” after the coup.
D-G: Drugs that empty the bowels have a bad effect on the brain

56.
A.Although there are large regional variations, it is not infrequent to find a large number of people sitting here and there and doing nothing.
B.Once in office, they receive friends and relatives who feel free to call any time without prior appointment.
C.While working, one is struck by the slow and clumsy actions and reactions, indifferent attitudes, procedure rather than outcome orientation, and the lack of consideration for others.
D.Even those who are employed often come late to the office and leave early unless they are forced to be punctual.
E.Work is not intrinsically valued in India.
F. Quite often people visit ailing friends and relatives or go out of their way to help them in their personal matters even during office hours.

(a) ECADBF

(b) EADCFB

(c) EADBFC
(d) ABFCBE

Ans .
(c)

Explanation:
Out of the options for first sentence E/A, E seems better. Then, E–A forms a mandatory pair as it moves from the general “India” to specific “regional variations”. D–B’ is the second mandatory pair with “office” being mentioned in D and then B starting with “office”. This makes choice (c) correct

57.A.But in the industrial era destroying the enemy’s productive capacity means bombing the factories which are located in the cities.
B.So in the agrarian era, if you need to destroy the enemy’s productive capacity, what you want to do is burn his fields, or if you’re really vicious, salt them.
C.Now in the information era, destroying the enemy’s productive capacity means destroying the information infrastructure.
D. How do you do battle with your enemy?
E. The idea is to destroy the enemy’s productive capacity, and depending upon the economic foundation, that productive capacity is different in each case.
F. With regard to defence, the purpose of the military is to defend the nation and be prepared to do battle with its enemy.

(a) FDEBAC

(b) FCABED

(c) DEBACF
(d) DFEBAC

Ans .
(a)

Explanation:
Between D and F, you are more likely to choose D as the opening sentence as it is a question, but if D comes first, sentence F would be general and will take the sequence of information back. Therefore, choose F as the opening sentence. F–D seems better than F–C. Also B–A–C is a mandatory sequence as they are all comparing the scenario between different contexts. This makes choice (a) correct.

58. A.Michael Hofman, a poet and translator, accepts this sorry fact without approval or complaint. B.But thanklessness and impossibility do not daunt him. C.He acknowledges too — in fact, he returns to the point often — that best translators of poetry always fail at some level. D.Hofman feels passionately about his work and this is clear from his writings. E.In terms of the gap between worth and rewards, translators come somewhere near nurses and street-cleaners.

(a) EACDB

(b) ADEBC

(c) EACBD
(d) DCEAB

Ans .
(c)

Explanation:
Only E can start this paragraph. AC follows in (a) and (c). B with ‘but’ is the point of inflexion and D ends the paragraph on an optimistic note. Hence, option (c) is correct.

59. A.Passivity is not, of course, universal.
B.In areas where there are no lords or laws, or in frontier zones where all men go armed, the attitude of the peasantry may well be different.
C.So indeed it may be on the fringe of the unsubmissive.
D. However, for most of the soil-bound peasants the problem is not whether to be normally passive or active, but when to pass from one state to another. E. This depends on an assessment of the political situation.

(a) BEDAC

(b) CDABE

(c) EDBAC
(d) ABCDE

Ans .
(d)

Explanation:
Among the options, the best options for the opening sentence seem to be A and B. Again the option with B as the first sentence does not flow logically. A-B is a better sequence as it moves from general (universal) to specific (in areas..). This makes choice (d) correct. Hence, option (d) is correct.

60. A.The situations in which violence occurs and the nature of that violence tends to be clearly defined at least in theory, as in the proverbial Irishman’s question: “Is this a private fight or can anyone join in?”
B.So the actual risk to outsiders, though no doubt higher than our societies, is calculabel.
C.Probably the only uncontrolled applications of force are those of social superiors to social inferiors and even here there are probably some rules. D. However, binding the obligation to kill, members of feuding families engaged in mutual massacre will be genuinely appalled if by some mischance a bystander or outsider is killed.
D. However, for most of the soil-bound peasants the problem is not whether to be normally passive or active, but when to pass from one state to another.
E. This depends on an assessment of the political situation.

(a) DABC

(b) ACDB

(c) CBAD
(d) DBAC

Ans .
(a)

Explanation:
BC is a mandatory pair with ‘calculabel’ and ‘only uncontrolled applications’ (exceptions to B). Hence, option (a) is correct.

61.But ___ are now regularly written not just for tools, but well-established practices, organisations and institutions, not all of which seem to be ___ away.

(a) reports ... withering

(b) stories ... trading

(c) books ... dying
(d) obituaries ... fading

Ans .
(d)

Explanation:
It’s choice (d). You don’t write reports or stories or books for tools, but ‘obituaries’ — yes, as tools do get obsolete. Also ‘practices’ do not wither or trade or die away, but they do fade away with time.

62.The Darwin who ___ is most remarkable for the way in which he ___ the attributes of the world class thinker and head of the household.

(a) comes ... figures

(b) arises ... adds

(c) emerges ... combines
(d) appeared ... combines

Ans .
(c)

Explanation:
You do not add or figure two attributes, but you do combine them into one. ‘Appear’ again is too abrupt when you are discerning a personality, ‘emerges’ would be more appropriate.

63.Since her face was free of ___ there was no way to ___ if she appreciated what had happened.

(a) make-up ... realise

(b) expression ... ascertain

(c) emotion ... diagnose
(d) scars ... understand

Ans .
(b)

Explanation:
The sentence is drawing a correlation between her face and her understanding. Scars and make-up are irrelevant in this context and can be removed as irrelevant options. “To diagnose if she appreciated” is incorrect, you diagnose on the basis of symptoms. This leaves us with option (b) which fits in well to make a coherent sentence.

64. In this context, the ___ of the British labour movement is particularly ___. .

(a) affair ... weird

(b) activity ... moving

(c) experience ... significant
(d) atmosphere ... gloomy

Ans .
(c)

Explanation:
Choice (a) with “weird” as an option can be removed and similarly choice (d) with “gloomy”. They are both using words that are not first-priority as they are somewhat informal. Out of the other choices, “activity” is not qualified as “moving” (emotional). Choice (c) fits in the best and is the answer

65. Indian intellectuals may boast, if they are so inclined, of being ___ to the most elitist among the intellectual ___ of the world.

(a) subordinate ... traditions

(b) heirs ... cliques

(c) ancestors ... societie
(d) heir ... traditions

Ans .
(d)

Explanation:
Choice (a) can be easily eliminated since “being subordinate” and “boasting” of it do not go together. Choice (c) is incorrect because ‘intellectuals’ (individuals) being ancestors to societies (collectivity) is incorrect. Also present Indian intellectuals cannot possibly be ancestors either. Choice (b) is incorrect because “intellectual cliques” is odd especially since “cliques” is used in a somewhat negative sense. Choice (d) is correct.

66.Specious: A specious argument is not simply a false one but one that has the ring of truth.

(a) Deceitful

(b) Fallacious

(c) Credible
(d) Deceptive

Ans .
(c)

Explanation:
A specious argument sounds true but is actually false. ‘Credible’ has a positive note against the other three choices.

67. Obviate: The new mass transit system may obviate the need for the use of personal cars.

(a) Prevent

(b) Forestall

(c) Preclude
(d) Bolster

Ans .
(d)

Explanation:
To obviate is to make something unnecessary, this meaning is elucidated in (a), (b) and (c). ‘Bolster’ on the other hand strengthens the cause of driving personal cars.

68.Disuse: Some words fall into disuse as technology makes objects obsolete.

(a) Prevalent

(b) Discarded

(c) Obliterated
(d) Unfashionable

Ans .
(a)

Explanation:
Easy. (b) (c) and (d) actually mean something that is no longer in use. (a) talks about prevailing practices

69. Parsimonious: The evidence was constructed from very parsimonious scraps of information.

(a) Frugal

(b) ) Penurious

(c) Thrifty
(d) Altruistic

Ans .
(d)

Explanation:
Parsimonious means being stingy. Choices (a), (b) and (c) are similar making choice (d) the answer.

70.Facetious: When I suggested that war is a method of controlling population, my father remarked that I was being facetious

(a) Jovian

(b) Jovia

(c) Jocular
(d) Joking

Ans .
(a)

Explanation:
To say that war is a remedy for the burgeoning population problem is to speak flippantly. (b), (c) and (d) convey this light tone. Jovian relates to the planet Jupiter.

71. When the author writes ‘globalising our social inequities’, the reference is to

(a) going beyond an internal deliberation on social inequity.

(b) dealing with internal poverty through the economic benefits of globalisation

(c) going beyond an internal delimitation of social inequity.
(d) achieving disadvantaged people’s empowerment, globally.

Ans .
(a)

Explanation:
The reference is to an open discussion of the caste issue on a global platform

72. According to the author, ‘inverted representations as balm for the forsaken’

(a) is good for the forsaken and often deployed in human histories.

(b) is good for the forsaken, but not often deployed historically for the oppressed.

(c) occurs often as a means of keeping people oppressed.
(d) occurs often to invert the status quo.

Ans .
(c)

Explanation:
Referring to paragraph 1, lines (7-8) its obvious that choice (c) is correct. “Inverted representations .... such inversions

73.Based on the passage, which broad areas unambiguously fall under the purview of the UN conference being discussed?

A. Racial prejudice
B. Racial pride
C. Discrimination, racial or otherwise
D. Caste-related discrimination
E. Race-related discrimination

(a) A and E

(b) C and E

(c) A, C and E
(d) B, C and D

Ans .
(a)

Explanation:
Clearly, the UN conference is looking at discriminations based on caste, especially looking at paragraph 1. Choices (A) and (E) mention that choice (B) is a positive area and is not being addressed and choices (C) and (D) are too broad. This makes choice (a) correct.

74. According to the author, the sociologist who argued that race is a ‘biological’ category and caste is a ‘social’ one,

(a) generally shares the same orientation as the author’s on many of the central issues discussed

(b) tangentially admits to the existence of ‘caste’ as a category.

(c) admits the incompatibility between the people of different race and caste.
(d) admits indirectly that both caste-based prejudice and racial discrimination exist.

Ans .
(b)

Explanation:
Paragraph 2, line 5 clearly indicates that choice (b) is correct.

75.An important message in the passage, if one accepts a dialectic between nature and culture, is that

(a) the results of the Human Genome Project reinforces racial differences.

(b) race is at least partially a social construct.

(c) discrimination is at least partially a social construct.
(d) caste is at least partially a social construct.

Ans .
(b)

Explanation:
The author mentions in paragraph 2, line 3 – “race is a biological category” and in the last paragraph line 5 – “It would thus seem ... that dialectic”. This means all biological constructs are social constructs of which race is one. This makes choice (b) correct.

76.From the following statements, pick out the true statement according to the passage.

(a) A mono-syllabic word can have only one onset.

(b) A mono-syllabic word can have only one rhyme but more than one rime.

(c) A mono-syllabic word can have only one phoneme.
(d)All of these

Ans .
(a)

Explanation:
A mono-syllabic word has only one syllabel. So it can have only one onset. A phoneme, according to the passage, can be ‘initial’ and ‘final’.

77.Which one of the following is likely to emerge last in the cognitive development of a child?

(a) Rhyme

(b) Rime

(c) Onset
(d) Phoneme

Ans .
(d)

Explanation:
According to second last paragraph, line seven, it’s obvious that choice (d) is correct.

78. A phonological deficit in which of the following is likely to be classified as dyslexia?

(a) Phonemic judgement

(b) Onset judgement

(c) Rime judgement
(d) Any one or more of the above

Ans .
(d)

Explanation:
The last part of the first paragraph makes it clear that (d) is correct.

79. The Treiman and Zudowski experiment found evidence to support which of the following conclusions?

(a) At age six, reading instruction helps children perform both, the same-different judgement task.

(b) The development of onset-rime awareness precedes the development of an awareness of phonemes.

(c) At age four to five children find the onset-rime version of the same/different task significantly easier
(d) The development of onset-rime awareness is a necessary and sufficient condition for the development of an awareness of phonemes.

Ans .
(b)

Explanation:
According to the last para, lines 7-10. The Treiman and Zudowski experiment showed that ‘4 and 5-yearold children found the onset-rime version ... significantly easier ... only the 6-year-old ... were able to perform both versions ... with an equal level of success’.

80.The single-syllabel words Rhyme and Rime are constituted by the exact same set of
A. rime(s)
B. onset(s)
C. rhyme(s)
D. phonemes(s)

(a) A and B

(b) A and C

(c) A, B and C
(d)B, C and D

Ans .
(b)

Explanation:
Refer to the sentence in paragraph 2 — ‘rimes correspond to rhymes in single-syllabus words’.

81. Why will Billie Holiday survive many who receive longer obituaries?

(a)Because of her blues creations.

(b) Because she was not as self-destructive as some other blues exponents.

(c) Because of her smooth and mellow voice.
(d) Because of the expression of anger in her songs.

Ans .
(a)

Explanation:
Choice (b) is false because the author says in paragraph one, line 4 “Few people ...”. Choice (c) is false because the author says “ ... Coarse-textured ....” in the fifth last line of the first para. Choice (d) is also incorrect as revealed in the last part of the passage. Choice (a) is correct as the author’s appreciation is for her singing though he does pay attention to other aspects of her life.

82.According to the author, if Billie Holiday had not died in her middle age

(a) she would have gone on to make a further mark.

(b) she would have become even richer than what she was when she died.

(c) she would have led a rather ravaged existence.
(d) she would have led a rather comfortable existence.

Ans .
(c)

Explanation:
The answer is presented in the fourth last line of the first para, “what middle age ..”. This makes choice (c) correct.

83. Which of the following statements is not representative of the author’s opinion?

(a) Billie Holiday had her unique brand of melody

(b) Billie Holiday’s voice can be compared to other singers in certain ways.

(c) Billie Holiday’s voice had a ring of profound sorrow.
(d) Billie Holiday welcomed suffering in her profession and in her life.

Ans .
(d)

Explanation:
The answer to this is also presented directly in the last line of the second paragraph — “suffering was her ....” . This makes choice (d) correct.

84.According to the passage, Billie Holiday was fortunate in all but one of which of the following ways?

(a)She was fortunate to have been picked up young by an honest producer.

(b) She was fortunate to have the likes of Louis Armstrong and Bessie Smith accompany her.

(c) She was fortunate to possess the looks.
(d) She enjoyed success among the public and connoisseurs

Ans .
(b)

Explanation:
Billie Holiday was fortunate to have ‘the best musicians of the 1930s to accompany her — notably Teddy Wilson, Frankie Newton and Lester Young ...’

85. How is Kurosawa able to show the erosion of Dersu’s way of life?

(a) By documenting the ebb and flow of modernisation.

(b) By going back farther and farther in time.

(c) By using three different time frames and shifting them.
(d) Through his death in a distant time.

Ans .
(c)

Explanation:
The author mentions in the first paragraph, lines 3-5, “Each of the ....”. This makes choice (c) correct

86. Arseniev’s search for Dersu’s grave

(a) is part of the beginning of the film

(b) symbolises the end of the industrial society.

(c)is misguided since the settlement is too new.
(d) symbolises the rediscovery of modernity

Ans .
(a)

Explanation:
Refer to the part ‘The film itself ... opening by Dersu’s grave’. Besides (a) can be easily inferred from the second paragraph

87.The film celebrates Dersu’s wisdom

(a) by exhibiting the moral vacuum of the pre-modern world.

(b) by turning him into a mythical figure.

(c) through hallucinatory dreams and visions
(d) through Arseniev’s nostalgic, melancholy ruminations

Ans .
(d)

Explanation:
The answer is presented directly in lines 2-4 of the third paragraph. “... nostalgic, melancholy...”. The answer is presented directly in lines 2-4of the third paragraph. “... nostalgic, melancholy...”.

88.According to the author, the section of the film following the prologue

(a)serves to highlight the difficulties that Dersu faces that eventually kills him.

(b) shows the difference in thinking between Arseniev and Dersu.

(c) shows the code by which Dersu lives that allows him to survive his surroundings.
(d) serves to criticize the lack of understanding of nature in the pre-modern era.

Ans .
(c)

Explanation:
The answer is in lines 4-6 of the third paragraph. “First section of ....”. This makes choice (c) is correct.

89.In the film, Kurosawa hints at Arseniev’s reflective and sensitive nature

(a) by showing him as not being derisive towards Dersu, unlike other soldiers.

(b) by showing him as being aloof from other soldiers.

(c) through shots of Arseniev writing his diary, framed by trees
(d) All of these

Ans .
(d)

Explanation:
This aspect is highlighted in the last paragraph and choice (d) is the answer

90. According to the author, which of these statements about the film is correct?

(a) The film makes its arguments circuitously.

(b) The film highlights the insularity of Arseniev.

(c) The film begins with the absence of its main protagonist.
(d) None of these

Ans .
(c)

Explanation:
Refer to the part ‘Kurosawa defines the world of the film initially upon a void, a missing presence’.

91. Dynamic leaders are needed in democracies because

(a) they have adopted the principles of ‘formal’ equality rather than ‘substantive’ equality.

(b) ‘formal’ equality whets people’s appetite for ‘substantive’ equality.

(c)systems that rely on the impersonal rules of ‘formal’ equality lose their ability to make large changes
(d) of the conflict between a ‘progressive’ executive and a ‘conservative’ judiciary.

Ans .
(c)

Explanation:
Refer to the seventh paragraph lines 4-5 ‘... the greater the urge for change in a society, the stronger the appeal of a dynamic leadership ...’ This makes choice (c) correct.

92.What possible factor would a dynamic leader consider a ‘hindrance’ in achieving the development goals of a nation?

(a) Principle of equality before the law

(b)Judicial activism

(c) A conservative judiciary
(d) Need for discipline

Ans .
(a)

Explanation:
The answer to this question is present in the last paragraph in the second line “From the argument....” This makes choice (a) correct

93.Which of the following four statements can be inferred from the above passage? A.Scientific rationality is an essential feature of modernity.
B.Scientific rationality results in the development of impersonal rules.
C.Modernisation and development have been chosen over traditional music, dance and drama.
D.Democracies aspire to achieve substantive equality.

(a) A, B, D but not C

(b) A, B but not C, D

(c) A, D but not B, C
(d) A, B, C but not D

Ans .
(a)

Explanation:
Choice (A) is present in paragraph four, line one, choice (B) is mentioned in the last line of the fourth paragraph and choice (D) is mentioned in the 3rd last line of the seventh para. This makes choice (a) correct.

94.Tocqueville believed that the age of democracy would be an un-heroic age because

(a) democractic principles do not encourage heroes.

(b) there is no urgency for development in democratic countries.

(c) heroes that emerged in democracies would become despots.
(d)aristocratic society had a greater ability to produce heroes.

Ans .
(a)

Explanation:
The answer is presented in lines 1 to 4 of paragraph 2. This makes choice (a) correct.

95.A key argument the author is making is that

(a) in the context of extreme inequality, the issue of leadership has limited significance.

(b) democracy is incapable of eradicating inequality.

(c)) formal equality facilitates development and change.
(d) impersonal rules are good for avoiding instability but fall short of achieving real equality.

Ans .
(d)

Explanation:
Refer to the first line of the fifth paragraph — ‘But a system governed solely by impersonal rules can at best ensure order and stability; it cannot ... formal equality will be replaced by real equality ...’ This makes choice (d) correct.

96. Which of the following four statements can be inferred from the above passage? A.There is conflict between the pursuit of equality and individuality. B.The disadvantages of impersonal rules can be overcome in small communities.
C.Despite limitations, impersonal rules are essential in large systems.
D.Inspired leadership, rather than plans and schemes, is more effective in bridging inequality

(a) B, D but not A, C

(b) A, B but not C, D

(c) A, D but not B, C
(d) A, C but not B, D

Ans .
(c)

Explanation:
A can be inferred, refer to the part — ‘Democracy rests on two different principles ... the principle of equality before the law ... the leadership principle ... one principle cannot be promoted without some sacrifice of the other... ’ D can be inferred, refer to the part — ‘their continued preoccupation with plans and schemes ... to bridge the gap between the ideal of equality and the reality which is so contrary to it ... leadership with a measure of charisma ...’ B and C venture too far by using the words ‘disadvantages’ and ‘limitations’ respectively which have no contextual relevance.

97.In the passage, the Dark Age refers to

(a)the period when the universe became cold after the Big Bang.

(b) a period about which astronomers know very little.

(c) the medieval period when cultural activity seemed to have come to an end
(d) the time that the universe took to heat up after the Big Bang.

Ans .
(b)

Explanation:
The second and third lines of the second paragraph mention “Dark Age...” this makes choice (b) correct

98.Astronomers find it difficult to study the Dark Age because

(a) suitable telescopes are few.

(b) the associated events took place aeons ago.

(c) the energy source that powers a quasars is unknown.
(d) their best chance is to study quasars, which are faint objects to begin with.

Ans .
(b)

Explanation:
Lines one to three of the fourth paragraph mention “The main problem...” making choice (b) the answer.

99. The four most distant quasars discovered recently

(a) could only be seen with the help of large telescopes.

(b) appear to be similar to other ordinary, quasars.

(c)appear to be shrouded in a fog of hydrogen gas.
(d) have been sought to be discovered by Dark Age astronomers since 1965.

Ans .
(a)

Explanation:
Lines three-five of the fifth paragraph “Recently, some members ...” makes choice (a) correct.

100. The fog of hydrogen gas seen through the telescopes

(a) is transparent to hydrogen radiation from stars and quasars in all states.

(b) was lifted after heat from starts and quasars ionised it.

(c)is material which eventually became stars and quasars.
(d) is broken into constituent elements when stars and quasars are formed.

Ans .
(b)

Explanation:
As revealed in the first line of the last paragraph, choice (b) is correct.

101.How many lays are used to produce yellow fabrics?

(a)10

(b)11

(c)12
(d)14

Ans .
(d)

Explanation:
Count only those lays for which any size of yellow coloured fabric is produced. They are lay number 1, 3, 4, 6, 7, 8, 9, 11, 12, 15, 21, 24, 25, 27 Hence, 14 is the answer

102. How many lays are used to produce XXL fabrics?

(a)15

(b)16

(c)17
(d)18

Ans .
(b)

Explanation:
Count those lays for which extra-extra large fabric is produced of any colours, i.e. count the lay numbers for which at least one of XXL from 3 colours is nonzero. They are lay number 7, 8, 9, 10, 11, 12, 13, 14, 15, 21, 22, 23, 24, 25, 26, 27 . Hence, 16 is the answer

103.How many lays are used to produce XL yellow or XL white fabrics?

(a)8

(b)9

(c)10
(d)15

Ans .
(d)

Explanation:
Again count lay number for which at least one of the XXL from yellow and white are non-zero. Lay number 7, 8, 9, 10, 11, 12, 13, 14, 15, 21, 23, 24, 25, 26, 27. Hence, 15 is the answer.

104. How many varieties of fabrics, which exceed the order, have been produced?

(a)3

(b)4

(c)5
(d)6

Ans .
(b)

Explanation:
The varieties for which there is surplus gives the answer. There are 4 such varieties.

105. How many international airports of type ‘A’ account for more than 40 million passengers?

(a)4

(b)5

(c)6
(d)7

Ans .
(b)

Explanation:
Put a decimal after the first two digit in the passengers column and it will give the figure in millions. In that case we have only 5 international airports of type A having more than 40 million passengers. They are in serial number 1, 2, 3, 5, 9. Rest all ‘A’ type airports are below 40 million.

106.What percentage of top ten busiest airports is in the United States of America?

(a) 60%

(b) 80%

(c) 70%
(d) 90%

Ans .
(a)

Explanation:
There are only six airports of USA among the top 10 busiest airports. They are in serial number 1, 2, 3, 5, 9, 10. \( \frac{6}{10} \)× 100 = 60%

107.Of the five busiest airports, roughly, what percentage of passengers in handled by Heathrow Airport?

(a)30

(b)40

(c)20
(d)50

Ans .
(c)

Explanation:
We have to calculate the percentage of passengers handled at Heathrow Airport. Now total number of passengers in the 5 busiest airport is approximately (77 + 72 + 63 + 62 + 60) million = 334 million At Heathrow it is 62 millionThe approximate percentage is \( \frac{60}{300} \)× 100 =20%

108.How many international airports not located in the USA handle more than 30 million passengers?

(a)5

(b)6

(c)10
(d)14

Ans .
(b)

Explanation:
All the international airports handle more than 30 million passengers. Among these only 6 airports are not located in USA. Hence, (b) is the correct option.

109. Which work requires as many man-hours as that spent in coding?

(a) Offshore, design and coding

(b)) Offshore coding

(c)Testing
(d) Offshore, testing and coding

Ans .
(a)

Explanation:
Man-hours spent in coding is 420 + 100 = 520. Now going by options, we see (a) is the only option.

110. Roughly, what percentage of the total work is carried out onsite?

(a) 40%

(b) 20%

(c) 30%
(d) 10%

Ans .
(c)

Explanation:
Total work is approximately (100 + 80) + (420 + 100) + (280 + 140) = 1120 On-site work = 80 + 100 + 140 = 320 Percentage of total work carried out on-site is \( \ frac{320} frac{1120} \)× = 30% approximatly

111.The total effort in man-hours spent onsite is nearest to which of the following?

(a)The sum of the estimated and actual effort for offshore design.

(b) The estimated man-hours of offshore coding.

(c) The actual man-hours of offshore testing.
(d) Half of the man-hours of estimated offshore coding.

Ans .
(c)

Explanation:
From figure the total effort in man-hours spent on-site is 320. It is nearest to actual man-hours of offshore testing which is 280 (approximately.)

112. If the total working hours were 100, which of the following tasks will account for approximately 50 hr?

(a) Coding

(b) Design

(c) Offshore testing
(d) Offshore testing plus design

Ans .
(a)

Explanation:
Total man-hours = (100 + 80) + (420 + 100) + (280 + 140) = 1120. Total working hours = 100 Total man working = 1120/100 = 11.2 or 11. For 50 hr the total man-hours is 50 × 11 = 550 which is near to coding (420 + 100) Hence, (a) is the answer

113.If 50% of the offshore work were to be carried out onsite, with the distribution of effort between the tasks remaining the same, the proportion of testing carried out offshore would be

(a)40%

(b)30%

(c)50%
(d)60%

Ans .
(b)

Explanation:
Initial offshore testing man-hours = 280. Initial onshore testing man-hours = 140. Final offshore testing man-hours = 280 - 50% of 280 = 140 Final onshore testing man-hours = 140 + 140 = 280. Hence, the proportion of testing offshore =\( \frac{140} frac{140+280} \) = 30%

114. If 50% of the offshore work were to be carried out onsite, with the distribution of effort between the tasks remaining the same, which of the following is true of all work carried out onsite?

(a) The amount of coding done is greater than that of testing.

(b)The amount of coding done onsite is less than that of design done onsite.

(c) The amount of design carried out onsite is greater than that of testing.
(d) The amount of testing carried out offshore is greater than that of total design.

Ans .
(a)

Explanation:

115. The quantity moved from Avanti to Vidisha is

(a)200

(b)800

(c)700
(d)1000

Ans .
(d)

Explanation:
We can see that the flow from Vaishali to Jyotishmati is 300 whereas demand is 400, so the deficit 100 will be met by flow from Vidisha. Again, the demand of 700 in Panchal is to be met by flow from Jyotishmati which can get it from Vidisha. Thus, the quantity moved from Avanti to Vidisha 200 + 100 + 700 = 1000

116.The free capacity availabel at the Avanti-Vaishali pipeline is

(a)0

(b)100

(c)200
(d)300

Ans .
(d)

Explanation:
Free capacity at Avanti-Vaishali pipeline is 300, since capacity of each pipeline is 1000 and demand at Vidisha is 400 and 300 flows to Jyotishmati. Thus, free capacity = {1000 – (400 + 300)} = 300

117. What is the free capacity availabel in the Avanti-Vidisha pipeline?

(a)300

(b)200

(c)100
(d)0

Ans .
(d)

Explanation:
Free capacity in Avanti-Vidisha is zero. Explanation is similar as in previous answer.

118. Suppose effort allocation is inter-changed between operations B and C, then C and D, and then D and E. If companies are then ranked in ascending order of effort in E, what will be the rank of company 3?

(a)2

(b)3

(c)4
(d)5

Ans .
(b)

Explanation:
On interchanging the effort allocation between operations B and C, then C and D, and then D and E we find that B takes the E’s position. Looking at the effort in B and then ranking in ascending order we find that the company 3 ranks third.

119.A new technology is introduced in company 4 such that the total effort for operations B through F get evenly distributed among these. What is the change in the percentage of effort in operation E?

(a) Reduction of 12.3

(b) Increase of 12.3

(c) Reduction of 5.6
(d) Increase of 5.6

Ans .
(a)

Explanation:
Total effort for operation B through F is 81.5%. Even distribution will give effort allocation in each operation = % 3.16 5 /5.81 = ∴Change in E = 28.6 – 16.3 = 12.3%

120. Suppose the companies find that they can remove operations B, C and D and redistribute the effort released equally among the remaining operations. Then which operation will show the maximum across all companies and all operations?

(a) Operation E in company 1

(b) Operation E in company 4

(c) Operation F in company 5
(d) Operation E in company 5

Ans .
(d)

Explanation:
Since we are given about company 1, 4, 5 in options so we will look for changes in these companies only. Allocation of effort in B, C, D in companies 1 = 43.1 Remaining operations gets % 4.14 3 1.43 = each. Allocation of effort in B, C, D operations of company 4 = 29.7 Remaining operation is allocated extra 29.7 9.9% 3 = each. Allocation of effort in B, C, D operation of company 5 = 36.8 Remaining operation is allocated 36.8=12.3% =3 = each. We see that operation E in company 5 will then show the maximum.

121.What are the values of m and n? I. n is an even integer, m is an odd integer, and m is greater than n.
II. Product of m and n is 30.

(a) if the question can be answered by one of the statements alone and not by the other.

(b) if the question can be answered by using either statement alone.

(c) if the question can be answered by using both the statements together, but cannot be answered by using either statement alone.
(d)if the question cannot be answered even by using both statements together.

Ans .
(c)

Explanation:
From statement II, m, n could be (2, 15) (5, 6), (3, 10) and (1, 30) but from statement I, we get m, n as (2, 15). Hence, the question can be answered by using both the statements together.

122. Is Country X’s GDP higher than country Y’s GDP? I. GDPs of the countries X and Y have grown over the past 5 years at compounded annual rate of 5% and 6% respectively. II. Five years ago, GDP of country X was higher than that of country Y.

(a) if the question can be answered by one of the statements alone and not by the other.

(b) if the question can be answered by using either statement alone

(c) if the question can be answered by using both the statements together, but cannot be answered by using either statement alone.
(d)by using either statement alone.

Ans .
(d)

Explanation:
From statement I nothing can be said since exact figures are not given. From statement II since X > Y (from B) we do not know how much X is greater than Y, because if it is slightly greater than it will be less than Y after 5 years whereas if the difference is very high, then X will be greater than Y even after 5 years.

123. What is the value of X? I. X and Y are unequal even integers, less than 10, and X Y is an odd integer.
II. X and Y are even integers, each less than 10, and product of X and Y is 12.

(a)if the question can be answered by one of the statements alone and not by the other.

(b) if the question can be answered by using either statement alone.

(c) if the question can be answered by using both the statements together, but cannot be answered by using either statement alone.
(d) if the question cannot be answered even by using both statements together.

Ans .
(a)

Explanation:
From statement I, unequal even integers less than 10 are 2, 4, 6 and 8. X/ Y is an odd integer is possible only if X = 6 and Y = 2 From statement II, even integers less than 10 are 2, 4, 6 and 8. XY = 12 ⇒ X = 6, Y = 2 or X = 2, Y = 6 Hence, question can be answered by using statement I alone but not by statement I

124. On a given day a boat ferried 1,500 passengers across the river in 12 hr. How many round trips did it make? I. The boat can carry 200 passengers at any time.
II. It takes 40 min each way and 20 min of waiting time at each terminal.

(a) if the question can be answered by one of the statements alone and not by the other.

(b) if the question can be answered by using either statement alone.

(c) if the question can be answered by using both the statements together, but cannot be answered by using either statement alone.
(d) if the question cannot be answered even by using both statements together.

Ans .
(a)

Explanation:
Statement I gives the capacity of boat and is of no help in finding out the number of round trips. From statement II round trips can be calculated since we know the total time taken is 12 hr.

125. What will be the time for downloading software? I. Transfer rate is 6 kilobytes per second.
II. The size of the software is 4.5 megabytes.

(a) if the question can be answered by one of the statements alone and not by the other.

(b)if the question can be answered by using either statement alone.

(c)if the question can be answered by using both the statements together, but cannot be answered by using either statement alone.
(d) if the question cannot be answered even by using both statements together.

Ans .
(c)

Explanation:
Statement I gives the rate and statement II gives the size. It is like statement I gives the speed and statement II the distance and we are to find out time. So both statements are needed

126. A square is inscribed in a circle. What is the difference between the area of the circle and that of the square? I. The diameter of the circle is 2 25 cm.
II. The side of the square is 25 cm.

(a)if the question can be answered by one of the statements alone and not by the other.

(b)if the question can be answered by using either statement alone.

(c)if the question can be answered by using both the statements together, but cannot be answered by using either statement alone.
(d)if the question cannot be answered even by using both statements together.

Ans .
(c)

Explanation:

We know that the diameter of circle will be the diagonal of the square. Thus, from any of the two statements, we can find out the areas of the circle and square.

127. Two friends, Ram and Gopal, bought apples from a wholesale dealer. How many apples did they buy? I. Ram bought one-half the number of apples that Gopal bought.
II. The wholesale dealer had a stock of 500 apples.

(a) if the question can be answered by one of the statements alone and not by the other.

(b)if the question can be answered by using either statement alone.

(c)if the question can be answered by using both the statements together, but cannot be answered by using either statement alone.
(d)if the question cannot be answered even by using both statements together

Ans .
(d)

Explanation:
Statement I gives a general figure of Ram and Gopal. Statement II does not give any idea of how many apples Ram and Gopal purchased. Both statements together also cannot give any result.

128.The cost in rupees per tonne of oil moved by rail and road happens to be roughly

(a) Rs. 3

(b)) Rs. 1.5

(c) Rs. 4.5
(d) Rs. 8

Ans .
(b)

Explanation:
Cost in rupees of oil moved by rail and road is 18% of 30 million = 5.4 million. Volume of oil transported by rail and road = 31% of 12 million tonnes = 3.72 million tonnes. Cost in rupees per tonnes = 5.4/3.72 = 1.5 approximately.

129. From the charts given, it appears that the cheapest mode of transport is

(a) road

(b)rail

(c) pipeline
(d) ship

Ans .
(a)

Explanation:
From the chart, we can make out the least among road, rail, pipeline, ship by looking at the ratio of cost to volume. Road = 6 /22 Rail = 9/ 12 Pipeline = 65/ 49 Ship = 10 /9 Since ratio of cost to volume for road is the lowest, it is the cheapest.

130.If the costs per tonne of transport by ship, air and road are represented by P, Q and R respectively, which of the following is true?

(a) R > Q > P

(b) P > R > Q

(c) P > Q > R
(d) R > P > Q

Ans .
(c)

Explanation:
Ship, air and road. Like the previous answer again look at ratio of \( \frac{10}{9} \), \( \frac{7}{11} \), \( \frac{6}{22} \)
so \( \frac{10}{9} \)> \( \frac{7}{11} \)> \( \frac{6}{22} \)
Hence, P>Q>R

131.At a village mela, the following six nautankis (plays) are scheduled as shown in the table below.

You wish to see all the six nautankis. Further, you wish to ensure that you get a lunch break from 12.30 p.m. to 1.30 p.m. Which of the following ways can you do this?

(a)Sati Savitri is viewed first; Sundar Kand is viewed third, and Jhansi ki Rani is viewed last

(b)Sati Savitri is viewed last; Veer Abhimanyu is viewed third, and Reshma aur Shera is viewed first

(c) Sati Savitri is viewed first; Sundar Kand is viewed third, and Joru ka Ghulam is viewed fourth
(d)Veer Abhimanyu is viewed third; Reshma aur Shera is viewed fourth, and Jahansi ki Rani is viewed fifth

Ans .
(c)

Explanation:
Sati-Savitri starts at the earliest. So we view it first. (1) Sati-Savitri — 9.00 a.m. to 10.00 a.m.
(2) Veer Abhimanu — 10.00 a.m. to 11.00 a.m. (3) Jhansi Ki Rani/Sundar Kand — 11.00 a.m. to 11.30 a.m. (4) Joru Ka Ghulam — 11.30 a.m. to 12.30 p.m. Now lunch break from 12.30 p.m. to 1.30 p.m. At 1.30 p.m. he can takes the show of only Jhansi Ki Rani so it cannot be viewed at 3rd. (5) Jhansi Ki Rani — 1.30 p.m. to 2.00 p.m. (6) Reshma aur Shera 2.00 p.m. to 3.00 p.m.
Hence, option (c) is best

132. Mrs Ranga has three children and has difficulty remembering their ages and months of their birth. The clue below may help her remember. • The boy, who was born in June, is 7 years old.
• One of the children is 4 years old but it was not Anshuman.
• Vaibhav is older than Suprita.
• One of the children was born in September, but it was not Vaibhav.
• Suprita’s birthday is in April.
• The youngest child is only 2-year-old.
Based on the above clues, which one of the following statements is true?

(a) Vaibhav is the oldest, followed by Anshuman who was born in September, and the youngest is Suprita who was born in April

(b)Anshuman is the oldest being born in June, followed by Suprita who is 4-year-old, and the youngest is Vaibhav who is 2-year-old

(c) Vaibhav is the oldest being 7-year-old, followed by Suprita who was born in April, and the youngest is Anshuman who was born in September
(d) Suprita is the oldest who was born in April, followed by Vaibhav who was born in June, and Anshuman who was born in September

Ans .
(c)

Explanation:
Three children Vaibhav, Suprita and Anshuman. Vaibhav > Suprita
↓
(Born in April) One of children is born in September, but it is not Vaibhav, so it has to be Anshuman. So Vaibhav is born in June and is 7-year-old.
Vaibhav is 7-year-old and Anshuman is not 4-year-old. So Suprita is 4-year-old. Youngest child is 2-year-old and it has to be Anshuman. Vaibhav > Suprita > Anshuman (June, 7 years) (April, 4 years) (Sept., 2-year-old) Hence, (c) is the answer.

133. The Bannerjees, the Sharmas, and the Pattabhiramans each have a tradition of eating Sunday lunch as a family. Each family serves a special meal at a certain time of day. Each family has a particular set of chinaware used for this meal. Use the clues below to answer the following question.
• The Sharma family eats at noon.
• The family that serves fried brinjal uses blue chinaware.
• The Bannerjee family eats at 2 o’clock.
• The family that serves sambar does not use red chinaware.
• The family that eats at 1 o’clock serves fried brinjal.
• The Pattabhiraman family does not use white chinaware.
• The family that eats last likes makkai-ki-roti. Which one of the following statements is true?

(a) The Bannerjees eat makkai-ki-roti at 2 o’clock, the Sharmas eat fried brinjal at 12 o’clock and the Pattabhiramans eat sambar from red chinaware

(b) The Sharmas eat sambar served in white chinaware, the Pattabhiramans eat fried brinjal at 1 o’clock, and the Bannerjees eat makkai-ki-roti served in blue chinaware

(c) The Sharmas eat sambar at noon, the Pattabhiramans eat fried brinjal served in blue chinaware, and the Bannerjees eat makkai-ki-roti served in red chinaware
(d)The Bannerjees eat makkai-ki-roti served in white chinaware, the Sharmas eat fried brinjal at 12 o’clock and the Pattabhiramans eat sambar from red chinaware

Ans .
(c)

Explanation:
We can find out the time for lunch of respective families from the table below:

Fried brinjal → Chinaware Sambar → White Chinaware Makkai-ki-roti → Red Chinaware
The family that eats at 1 o’clock serves fried brinjal, hence Pattabhiraman serves fried brinjal.
The family that eats last like makkai-ki-roti so Banaerjees like makkai-ki-roti. Sharmas are left with sambar. Sharma - 12:00 - Sambar - White Pattabhiraman - 1:00 - Fried brinjal - Blue Bannerjees - 2:00 - Makkai-ki-roti - Red Hence, (c) is the best option.

134. While Balbir had his back turned, a dog ran into his butcher shop, snatched a piece of meat off the counter and ran out. Balbir was mad when he realised what had happened. He asked three other shopkeepers, who had seen the dog, to describe it. The shopkeepers really did not want to help Balbir. So each of them made a statement which contained one truth and one lie. • Shopkeeper number 1 said: “The dog had black hair and a long tail.”
• Shopkeeper number 2 said: “The dog had a short tail and wore a collar.”
• Shopkeeper number 3 said: “The dog had white hair and no collar.”
Based on the above statements, which of the following could be a correct description?

(a)The dog had white hair, short tail and no collar

(b) The dog had white hair, long tail and a collar

(c)The dog had black hair, long tail and a collar
(d) The dog had black hair, long tail and no collar

Ans .
(b)

Explanation:

135. Which of the following can be inferred?

(a) Yogesh is older than Wahida

(b) Elle is older than Wahida

(c) Elle may be younger than Wahida
(d) None of these

Ans .
(b)

Explanation:
Elle is 3 times older than Yogesh and Zaheer is half the age of Wahida. If Wahida is 2x-year-old, then Zaheer is x. Now Yogesh > Zaheer ⇒ Yogesh > x Elle is 3 times older than Yogesh. Which means Elle is older than Wahida as 3x > 2x

136. Which of the following information will be sufficient to estimate Elle’s age? (a) Zaheer is 10-year-old

(a) Zaheer is 10-year-old

(b) Both Yogesh and Wahida are older than Zaheer by the same number of years

(c) Both (a) and (b)
(d) None of these

Ans .
(c)

Explanation:
From (a) Zaheer is 10-year-old means Wahida is 20-year-old. From (b) Yogesh and Wahida are older than Zaheer by same number of years. This means Yogesh is 20-year-old. Now Elle is 3 times older than Yogesh. Elle is 20 × 3 = 60-year-old. Hence, we see that both (a) and (b) statements are needed so the answer is (c).

137.Which of the following is a feasible group of three?

(a)David, Ram and Rahim

(b) Peter, Shyam and Rahim

(c) Kavita, David and Shyam
(d) Fiza, David and Ram

Ans .
(b)

Explanation:
Checking from options,
(a) David, Rama and Rahim Ram would like to be in the group only if Peter is there, so it is not feasible.
(b) Peter, Shyam and Rahim want to be selected together and none of them have problem or any conditions, hence feasible.
(c) Since Shyam is there, Rahim has to be but he is not also Fiza is not there which David insists so not feasible.
(d) Since Peter is not there Ram would not prefer that group, hence not feasible

138. Which of the following is a feasible group in four?

(a)Ram, Peter, Fiza and Rahim

(b) Shyam, Rahim, Kavita and David

(c)Shyam, Rahim, Fiza and David
(d) Fiza, David, Ram and Peter

Ans .
(c)

Explanation:
Looking at options, we see (c) is best as Shyam and Rahim is selected and Fiza is there when David is selected.
In (a) we see Shyam is not there with Rahim. In (b) Fiza is not there with David. In (d) Peter and David cannot go together as David would not like Peter in the group.

139. Looking at options, we see (c) is best as Shyam and Rahim is selected and Fiza is there when David is selected. In (a) we see Shyam is not there with Rahim. In (b) Fiza is not there with David. In (d) Peter and David cannot go together as David would not like Peter in the group.

(a) Kavita and Ram can be part of a group of four

(b) A group of four can have two women

(c) A group of four can have all four men
(d) None of these

Ans .
(d)

Explanation:
In Ist option — Kavita is in the group means David is there and David would not like Peter in the group, whereas Ram would like to be in the group if Peter is there so the statement cannot be true. 2nd option — If David is there, then only the group will have both women Kavita and Fiza, but in that case we see none of the rest could be the fourth person as Shyam and Rahim has to be together and Ram would be if Peter is there and David would not like Peter in the group, hence statement is false. 3rd option — It is not possible as Ram cannot go with Shyam and David with Peter. So none of the above statements are true.

140. On her walk through the park, Hamsa collected 50 coloured leaves, all either maple or oak. She sorted them by category when she got home, and found the following: There are exactly 6 red spotted maple leaves. There are exactly 22 maple leaves that are neither spotted nor red. How many oak leaves did she collect?

(a)22

(b)17

(c)25
(d)18

Ans .
(b)

Explanation:
Let S = spotted, NS = Non-spotted There are 50 coloured leaves and is given as red and non-red. We make the following table. Let 2n be number of red oak leaves where n is any natural number.

141. Eight people carrying food baskets are going for a picnic on motorcycles. Their names are A, B, C, D, E, F, G, and H. They have 4 motorcycles M1, M2, M3 and M4 among them. They also have 4 food baskets O, P, Q and R of different sizes and shapes and each can be carried only on motorcycles M1, M2, M3 and M4 respectively. No more than 2 persons can travel on a motorcycle and no more than one basket can be carried on a motorcycle. There are 2 husband-wife pairs in this group of 8 people and each pair will ride on a motorcycle together. C cannot travel with A or B. E cannot travel with B or F. G cannot travel with F, or H, or D. The husband-wife pairs must carry baskets O and P. Q is with A and P is with D. F travels on M1 and E travels on M2 motorcycles. G is with Q, and B cannot go with R. Who is travelling with H?

(a)A

(b)B

(c)C
(d)D

Ans .
(c)

Explanation:

142. In a family gathering there are 2 males who are grandfathers and 4 males who are fathers. In the same gathering there are 2 females who are grandmothers and 4 females who are mothers. There is at least one grandson or a granddaughter present in this gathering. There are 2 husband-wife pairs in this group. These can either be a grandfather and a grandmother, or a father and a mother. The single grandfather (whose wife is not present) has 2 grandsons and a son present. The single grandmother (whose husband is not present) has 2 grand daughters and a daughter present. A grandfather or a grandmother present with their spouses does not have any grandson or granddaughter present. What is the minimum number of people present in this gathering?

(a)10

(b)12

(c)14
(d)16

Ans .
(b)

Explanation:

143.I have a total of Rs. 1,000. Item A costs Rs. 110, item B costs Rs. 90, item C costs Rs. 70, item D costs Rs. 40 and item E costs Rs. 45. For every item D that I purchase, I must also buy two of item B. For every item of A, I must buy one item of C. For every item E, I must also buy two of item D and one of item B. For every item purchased I earn 1,000 points and for every rupee not spent I earn a penalty of 1,500 points. My objective is to maximise the points I earn. What is the number of items that I must purchase to maximise my points?

(a)13

(b)14

(c)15
(d)16

Ans .
(b)

Explanation:
The condition that maximise the number of points is D – 2 – 80 (40 × 2) B – 4 – 360 (90 × 4) C – 8 – 560 (70 × 8) 1000 ∴ In total there are 14 items.

144. Four friends Ashok, Bashir, Chirag and Deepak are out for shopping. Ashok has less money than three times the amount that Bashir has. Chirag has more money than Bashir. Deepak has an amount equal to the difference of amounts with Bashir and Chirag. Ashok has three times the money with Deepak. They each have to buy at least one shirt, or one shawl, or one sweater, or one jacket that are priced Rs. 200, Rs. 400, Rs. 600, and Rs. 1,000 a piece respectively. Chirag borrows Rs. 300 from Ashok and buys a jacket. Bashir buys a sweater after borrowing Rs. 100 from Ashok and is left with no money. Ashok buys three shirts. What is the costliest item that Deepak could buy with his own money?

(a) A shirt

(b)A shawl

(c) A sweater
(d) A jacket

Ans .
(b)

Explanation:
Bashir < Chirag. Now Chirag borrows Rs. 300 and Bashir Rs. 100 from Ashok. Ashok buys 3 shirt so he must have at least Rs. 1,000. Bashir is left with no money after buying a sweater and he had to borrow Rs.100 from Ashok means he had Rs. 500 with him. Ashok must have less than Rs. 1,500. Ashok has three times the money with Deepak. So Deepak cannot have Rs. 300 because Ashok must have Rs.1,000, again Deepak cannot have Rs. 500 because Ashok should have less than Rs.1,500. So Deepak has Rs. 400 for which he can purchase the shawl which is costliest.

145.In a ‘keep-fit’ gymnasium class there are 15 females enrolled in a weight-loss programme. They all have been grouped in any one of the five weight-groups W1, W2, W3, W4, or W5. One instructor is assigned to one weight-group only. Sonali, Shalini, Shubhra and Shahira belong to the same weightgroup. Sonali and Rupa are in one weight-group, Rupali and Renuka are also in one weight-group. Rupa, Radha, Renuka, Ruchika, and Ritu belong to different weight-groups. Somya cannot be with Ritu, and Tara cannot be with Radha. Komal cannot be with Radha, Somya, or Ritu. Shahira is in W1 and Somya is in W4 with Ruchika. Sweta and Jyotika cannot be with Rupali, but are in a weightgroup with total membership of four. No weight-group can have more than five or less than one member. Amita, Babita, Chandrika, Deepika and Elina are instructors of weight-groups with membership sizes 5, 4, 3, 2 and 1 respectively. Who is the instructor of Radha?

(a) Babita

(b) Elina

(c) Chandrika
(d) Deepika

Ans .
(d)

Explanation:

146. A king has unflinching loyalty from eight of his ministers M1 to M8, but he has to select only four to make a cabinet committee. He decides to choose these four such that each selected person shares a liking with at least one of the other three selected. The selected persons must also hate at least one of the likings of any of the other three persons selected.
M1 likes fishing and smoking, but hates gambling.
M2 likes smoking and drinking, but hates fishing.
M3 likes gambling, but hates smoking,
M4 likes mountaineering, but hates drinking,
M5 likes drinking, but hates smoking and mountaineering.
M6 likes fishing, but hates smoking and mountaineering.
M7 likes gambling and mountaineering, but hates fishing.
M8 likes smoking and gambling, but hates mountaineering.
Who are the four people selected by the king?

(a) M1, M2, M5 and M6

(b)M3, M4, M5 and M6

(c) M4, M5, M6 and M8
(d) M1, M2, M4 and M7

Ans .
(d)

Explanation:

Going by options, we have: (a) M does not hate at least one of the liking of any of the other 3 persons selected. (b) None of person shares the liking of at least one of the other selected. (c) None of the person shares a liking with at least one of the other three selected. (d) M1 shares liking with M2 and vice versa. M4 shares liking with M7 and vice versa. M1, M2 dislikes M7 liking. M4, M7 dislikes M2 liking. Hence, the answer is option (d).

147.Given that X = M .D is such that X = D. Which of the following is true?

(a) All dogs are mammals

(b)Some dogs are mammals

(c) X = ϕ
(d) All mammals are dogs

Ans .
(a)

Explanation:

X = M.D = M ∩ D X = D M ∩ D = D ⇒ D ⊂ M Thus, all dogs are mammals.

148.If Y = F . (D . V) is not a null set, it implies that

(a)all fish are vertebrates

(b) all dogs are vertebrates

(c)) some fish are dogs
(d) None of these

Ans .
(c)

Explanation:
VD(FY ∩∩= is not a null set means some F’s are D’s and some D’s are V’s . This implies some fish are dogs.

149. If Z = (P . D) ∪M, then

(a)The elements of Z consist of Pluto, the dog, or any other mammal

(b)Z implies any dog or mammal

(c) Z implies Pluto or any dog that is a mammal
(d) Z is a null set

Ans .
(a)

Explanation:
Z = (P ∩ D) ∪ M P ∩ D means Pluto, the dog. (P ∩ D) ∪ M means Pluto, the dog or any other mammal.

150. If P . A = ϕ and P ∪ A = D, then which of the following is true?

(a) Pluto and alsatians are dogs

(b) Pluto is an alsatian

(c) Pluto is not an alsatian
(d) D is a null set

Ans .
(c)

Explanation:
P.A = φ ; P ∪ A = D P ∩ A = φ means no alsatian is Pluto or Pluto is not an alsatian where dogs are composed of alsatian or Pluto or both