NCERT Class 12 Chapter – 1 : RELATIONS and FUNCTIONS

 

Q. Let A be the set of all students of a boys school. Show that the relation R in A given by R = {(a, b) : a is sister of b} is the empty relation and R′ = {(a, b) : the difference between heights of a and b is less than 3 meters} is the universal relation.

1. Since the school is boys school, no student of the school can be sister of any student of the school.

2. Hence we know, R = φ, showing that R is the empty relation.

3. It is also obvious that the difference between heights of any two students of the school has to be less than 3 meters.

4. This shows that R′ = A × A is the universal relation.

Q. Let T be the set of all triangles in a plane with R a relation in T given by R = {(T1, T2) : T1 is congruent to T}. Show that R is an equivalence relation.

1. R is reflexive, since every triangle is congruent to itself.

2. Further,(T1, T2) ∈ R ⇒ T1 is congruent to T2; T2 is congruent to T1 ⇒ (T2,T1) ∈ R

3. Hence we know, R is symmetric. Moreover, (T1, T2), (T2, T3) ∈ R ⇒ T1 is congruent to T2 and T2 is congruent to T3 so T1 is congruent to T3 ⇒ (T1, T3) ∈ R. Therefore we have, R is an equivalence relation.

Q. Let L be the set of all lines in a plane and R be the relation in L defined as R = {(L 1 , L 2 ) : L 1 is perpendicular to L2 }. Show that R is symmetric but neither reflexive nor transitive.

1. R is not reflexive, as a line L1 can not be perpendicular to itself, i.e., (L1,L1) ∉ R.

2. R is symmetric as (L1,L2) ∈ R. L1 is perpendicular to L2. L2 is perpendicular to L1. (L2,L1) ∈ R

3. R is not transitive. Indeed, if L1 is perpendicular to L2 and L2 is perpendicular to L3, then L1 can never be perpendicular to L3 in fact it will be parallel.

4. (L1, L2) ∈ R, (L2, L3) ∈ R but (L1,L3) ∉ R.

Q. Show that the relation R in the set {1, 2, 3} given by R = {(1, 1), (2, 2), (3, 3), (1, 2), (2, 3)} is reflexive but neither symmetric nor transitive.

1. R is reflexive, since (1, 1), (2, 2) and (3, 3) lie in R.

2. Also, R is not symmetric, as (1, 2) ∈ R but (2, 1) ∉ R.

3. Similarly, R is not transitive, as (1, 2) ∈ R and (2, 3) ∈ R but (1, 3) ∉ R.

Q. Show that the relation R in the set Z of integers given by R = {(a, b) : 2 divides a – b} is an equivalence relation.

1. R is reflexive, as 2 divides (a – a) for all a ∈ Z. Further, if (a, b) ∈ R, then 2 divides a – b.

2. Therefore we have, 2 divides b – a. Hence we know, (b, a) ∈ R, which shows that R is symmetric. Similarly, if (a, b) ∈ R and (b, c) ∈ R, then a – b and b – c are divisible by 2. Now, a – c = (a – b) + (b – c) is even

3. So, (a – c) is divisible by 2. This shows that R is transitive. Thus, R is an equivalence relation in Z.

Q. Let R be the relation defined in the set A = {1, 2, 3, 4, 5, 6, 7} by R = {(a, b) : both a and b are either odd or even}. Show that R is an equivalence relation. Further, show that all the elements of the subset {1, 3, 5, 7} are related to each other and all the elements of the subset {2, 4, 6} are related to each other, but no element of the subset {1, 3, 5, 7} is related to any element of the subset {2, 4, 6}.

1. Given any element a in A, both a and a must be either odd or even, so that (a, a) ∈ R. Further, (a, b) ∈ R ⇒ both a and b must be either odd or even ⇒ (b, a) ∈ R.

2. Similarly, (a, b) ∈ R and (b, c) ∈ R ⇒ all elements a, b, c, must be either even or odd simultaneously ⇒ (a, c) ∈ R. Hence we know, R is an equivalence relation.

3. Further, all the elements of {1, 3, 5, 7} are related to each other, as all the elements of this subset are odd. Similarly, all the elements of the subset {2, 4, 6} are related to each other, as all of them are even

4. Also, no element of the subset {1, 3, 5, 7} can be related to any element of {2, 4, 6}, as elements of {1, 3, 5, 7} are odd, while elements of {2, 4, 6} are even.

EXERCISE – 1.1

Q-1: Check each and every relation whether the following are symmetric, reflexive and transitive:

(i) The relation R of the set S = {2, 3, 4, 5, 6, 7, 8, 9. . . . . . . . 15} is defined as

R = {(a, b): 2a – b = 0}

(ii) The relation R of the set S having natural numbers is defined as

R = {(a, b): b = 2a + 6 and a < 5}

(iii) The relation R of the set S = {2, 3, 4, 5, 6, 7} is defined as

R = {(a, b): b is divisible by a}

(iv) The relation R of the set S having only the integers is defined as

R = {(a, b): a – b is an integer}

(v) The relation R from the set H having human beings at a particular time in the town is given by:

(a) R = {(a, b): a and b is working at the same place}

(b) R = {(a, b): a and b are living in the same society}

(c) R = {(a, b): a is exactly 6 cm taller than b}

(d) R = {(a, b): b is husband of a}

(e) R = {(a, b): a is the father of b}

 

Answer:

(i) S = {2, 3, 4, 5, 6 . . . . . . . 13, 14, 15}

R = {(a, b) : 2a – b = 0}

Therefore we have, R = {(2, 4), (3, 6), (4, 8), (5, 10), (6, 12), (7, 14)}

In this case,

(2, 4) ɛ R, but also (4, 2) \(\notin\) R, i.e.,

[2 (4) – 2 ≠ 0]

So, R is not symmetric, by definition of symmetric functions.

(2, 2), (3, 3)………..,(15, 15) \(\notin\) R.

So, R is not reflexive, by definition of reflexive functions.

Since, (2, 4), (4, 8) ɛ R, but (2, 4) \(\notin\) R

As, [2(2) – 8 ≠ 0]

So, Also, R is not transitive, by definition of transitive functions.

Therefore we have, R, is neither reflexive nor transitive and nor symmetric.

(ii) R = {(a, b) : b = 2a + 6 and a < 5}

Therefore we have, R = {(1, 8), (2, 10), (3, 12), (4, 14)}

In this case,

(1, 8) ɛ R, but (8, 1) \(\notin\) R, i.e.,

So, R is not symmetric by definition of symmetric functions.

(1, 1) , (2, 2), . . . . . . . . . . . . . . . \(\notin\) R.

So, R is not reflexive by definition of reflexive functions.

Since, here there isn’t any pair in the form of (a, b) and (b, c) ɛ R, then (a, b) \(\notin\) R

So, R is not transitive by definition of transitive functions.

Therefore we have, R in this case is neither reflexive, nor transitive and nor symmetric.

(iii) S = {2, 3, 4, 5, 6, 7}

R = {(a, b): b is divisible by a}

(2, 4) ɛ R [as 4 isnt divisible by 2 completely]

(4, 2) \(\notin\) R [as 2 isnt divisible by 4]

So, R is not symmetric by definition of symmetric functions.

Each and every number is divisible at least by itself.

So, (a, a) ɛ R.

So, R is reflexive by definition of reflexive functions.

In this case,

As (a, b) and (b, c) ɛ R.

Then clearly, ‘b’ will be divisible by ‘a’ and ‘c’ will be divisible by ‘b’.

Therefore we have, c is divisible by b.

So, (a, b) ɛ R.

Hence we know, R is transitive by definition of transitive functions.

Therefore we have, R in this case is reflexive and transitive, but not symmetric.

 

(iv) R = {(a, b) : a – b will be any integer}

In this case,

For each a, b ɛ S, if (a, b) ɛ R, then

a – b is an integer.

\(\boldsymbol{\Rightarrow }\) – (a – b) will also be an integer.

\(\boldsymbol{\Rightarrow }\) (b – a) will also be an integer.

Therefore we have, (a, b) ɛ R.

Hence we know, R will be symmetric to each other.

For each a ɛ S, (a, a) ɛ R as, a – a = 0 which is also an integer.

Hence we know, R is reflexive by definition of reflexive functions.

Let, a pair in the form of (a, b) and (b, c) ɛ R, then (a, b, c) ɛ Z.

\(\boldsymbol{\Rightarrow }\) (a – b) and (b – c) is an integer.

\(\boldsymbol{\Rightarrow }\) a – c = (x – y) + (y – z) will also be an integer.

Hence we know, R is transitive by definition of transitive functions.

Therefore we have, R is reflexive, transitive and symmetric.

(v)

(a) R = {(a, b) : a and b is working at the same place}

In this case,

If (a, b) ɛ R, then a and b work at the same place

\(\boldsymbol{\Rightarrow }\) b and a will also work at the same place.

\(\boldsymbol{\Rightarrow }\) (b, a) ɛ R

Hence we know, R will be symmetric to each other by definition of symmetric functions.

For each 'a' ɛ S, (a, a) ɛ R as, ‘a’ and ‘a’ is working at the same place.

Hence we know, R is reflexive.

Let, a pair in the form of (a, b) and (b, c) ɛ R.

\(\boldsymbol{\Rightarrow }\) a and b is working at the same place, also b and c is working at the same place.

\(\boldsymbol{\Rightarrow }\) a and c is also working at the same place.

\(\boldsymbol{\Rightarrow }\) (a, c) ɛ R

Hence we know, R is transitive by definition of transitive functions.

Therefore we have, R is reflexive, transitive and symmetric .

 

(b) R = {(a, b) : a and b both are living in the same society}

In this case,

If (a, b) ɛ R, then ‘a’ and ‘b’ is living in the same society.

\(\boldsymbol{\Rightarrow }\) b and a will also live in the same society.

\(\boldsymbol{\Rightarrow }\) (b, a) ɛ R

Hence we know, R will be symmetric by definition of symmetric functions.

For each a ɛ S, (a, a) ɛ R as, ‘a’ and ‘a’ is the same human being.

Hence we know, R is reflexive by definition of reflexive functions.

Let, a pair in the form of (a, b) and (b, c) ɛ R.

\(\boldsymbol{\Rightarrow }\) a and b is living in the same society, also b and c is living in the same society.

\(\boldsymbol{\Rightarrow }\) a and c is also living in the same society.

\(\boldsymbol{\Rightarrow }\) (a, c) ɛ R

Hence we know, R is transitive by definition of transitive functions.

Therefore we have, R is reflexive, transitive and symmetric.

 

(c) R = {(a, b) : a is 6 cm taller than b}

In this case,

If (a, b) ɛ R, then a is 6 cm taller than b.

\(\boldsymbol{\Rightarrow }\) b can't be taller than a.

\(\boldsymbol{\Rightarrow }\) (b, a) \(\notin\) R

Hence we know, R is not symmetric to each other.

For each a ɛ S, (a, a) \(\notin\) R.

As, the same human being can’t be taller than himself.

So, ‘a’ can’t be taller than ‘a’.

Hence we know, R is not reflexive by definition of reflexive functions.

Let, a pair in the form of (a, b) and (b, c) ɛ R.

\(\boldsymbol{\Rightarrow }\) a is 6 cm taller than b, then b will be 6 cm taller than c.

\(\boldsymbol{\Rightarrow }\) a is atleast 12 cm taller than c.

\(\boldsymbol{\Rightarrow }\) (a, c) \(\notin\) R

Hence we know, R is not transitive by definition of transitive functions.

Therefore we have, R neither reflexive, nor transitive and nor symmetric.

 

(d) R = {(a, b) : b is the husband of a}

In this case,

If (a, b) ɛ R,

\(\boldsymbol{\Rightarrow }\) b is the husband of a.

\(\boldsymbol{\Rightarrow }\) a can’t be husband of b.

\(\boldsymbol{\Rightarrow }\) (b, a) \(\notin\) R

Instead of this, if ‘b’ is the husband of a, then ‘a’ is the wife of b.

Hence we know, R is not symmetric by definition of symmetric functions.

(a, a) \(\notin\) R

Since, b cannot be the husband of himself.

Hence we know, R is not reflexive by definition of reflexive functions.

If (a, b), (b, c) ɛ R

\(\boldsymbol{\Rightarrow }\) b is the husband of a and a is the husband of c.

This cases are not possible.

\(\boldsymbol{\Rightarrow }\) (a, c) \(\notin\) R

Hence we know, R is not transitive by definition of transitive functions.

Therefore we have, R in this case neither reflexive, nor transitive and nor symmetric.

 

(e) R = {(a, b) : a is the father of b}

In this case,

If (a, b) ɛ R,

\(\boldsymbol{\Rightarrow }\) a is the father of b.

\(\boldsymbol{\Rightarrow }\) b can’t be the father of a.

Thus, b is either the son or daughter of a.

\(\boldsymbol{\Rightarrow }\) (b, a) \(\notin \) R

Hence we know, R is not symmetric by definition of symmetric functions.

(a, a) \(\notin\) R

Since, b cannot be the father of himself.

Hence we know, R is not reflexive by definition of reflexive functions.

Since, (a, b) ɛ R and (b, c) \(\notin \) R

\(\boldsymbol{\Rightarrow }\) a is the father of b, then b is the father of c.

\(\boldsymbol{\Rightarrow }\) a is not the father of c.

Indeed, a will be the grandfather of c.

\(\boldsymbol{\Rightarrow }\) (a, c) \(\notin\) R

Hence we know, R is not transitive.

Therefore we have, R is neither reflexive, nor transitive and nor symmetric.

 

 

Q-2: Prove that the relation M in the set M of the real numbers which is defined as

M = {(x, y): x ≤ y²} which is neither reflexive, nor transitive, nor symmetric.

Answer:

M = {(x, y): x ≤ y²}

We can see that (\(\frac{1}{2}, \; \frac{1}{2} \)) \(\notin\) R

As, \(\frac{1}{2} > \left (\frac{1}{2} \right)^{2}\)

Hence we know, M is not reflexive by definition of reflexive functions.

(1, 4) ɛ M as 1 < 4²

But, 4 is not lesser than 1

So, (4, 1) \(\notin\) M

Hence we know, M is not symmetric by definition of symmetric functions.

(3, 2) and (2, 1.5) ɛ M [as 3 < 2² = 4 and 2 < (1.5)² = 2.25]

But, 3 > (1.5)² = 2.25

So, (3, 1.5) \(\notin\) M

Hence we know, M is not transitive by definition of transitive functions.

Therefore we have, M is in this case neither transitive, nor symmetric, nor reflexive.

 

 

Q-3: Check whether the relation given below is reflexive, symmetric and transitive:

The relation M is defined in the set {2, 3, 4, 5, 6, 7} as M = {(x, y): y = x + 1}.

 

Answer:

Let us assume that:

S {2, 3, 4, 5, 6, 7}.

The relation M is defined on set S as:

M = {(x, y): y = x + 1}

Therefore we have, M = {(2, 3), (3, 4), (4, 5), (5, 6), (6, 7)}

We can observe that (2, 3) \(\notin \) M, but (3, 2) ɛ M.

Hence we know, M is not symmetric.

We need to find (x, x) \(\notin \) M, where x ɛ M.

(2, 2), (3, 3), (4, 4), (5, 5), (6, 6), (7, 7) ɛ M

Hence we know, M is not reflexive by definition of reflexive functions.

(2, 3), (3, 4) ɛ M

But, (2, 4) \(\notin \) M

Hence we know, M is not transitive by definition of transitive functions.

Therefore we have, M is in this case neither symmetric, nor reflexive, nor symmetric.

 

 

Q-4: Prove that the relation M in M which is defined as M = {(x, y): x ≤ y} is transitive and reflexive, but not symmetric.

 

Answer:

M = {(x, y): x ≤ y}

So, (x, x) ɛ M [as x = x]

Hence we know, M is reflexive by properties of functions and relations.

Then, (4, 6) ɛ M (as 4 < 6)

But, (4, 6) \(\notin \) M since, 6 is greater than 4.

Hence we know, M is not symmetric by properties of functions and relations.

Let, (x, y), (y, z) ɛ M

Then, x ≤ y and y ≤ z

\(\boldsymbol{\Rightarrow }\) x ≤ z

\(\boldsymbol{\Rightarrow }\) (x, z) \(\notin \) M

Hence we know, M is transitive by properties of functions and relations.

Therefore we have, M is reflexive and transitive, but not symmetric.

Q-5: Check that whether the relation M in M which is defined as M = {(x, y): x ≤ y³} is transitive, reflexive and symmetric.

 

Answer:

M = {(x, y): x ≤ y}

We can see that (\(\frac{1}{2}, \; \frac{1}{2} \)) \(\notin\)

As, \(\frac{1}{2} > \left (\frac{1}{2} \right)^{3}\)

Hence we know, M is not reflexive.

(1, 2) ɛ M as 1 < 2³ = 8

But, (2, 1) \(\notin\) M (as 2³ > 1)

Hence we know, M is not symmetric by properties of functions and relations.

We have,

(3, \(\frac{3}{2}\)), (\(\frac{3}{2}, \; \frac{6}{5} \)), as 3 < \(\left(\frac{3}{2} \right)^{3} \)) and (\(\frac{3}{2} < \left(\frac{6}{5} \right)^{3} \)

But, (3, \(\frac{6}{5} \)) \(\notin\) M as 3 > \(\left(\frac{6}{5} \right)^{3}\)

Hence we know, M is not transitive by properties of functions and relations.

Therefore we have, M is in this case neither symmetric, nor reflexive, nor transitive.

 

 

Q-6: Prove that the relation M from the set {2, 3, 4} which is given by M = {(2, 3), (3, 2)} is not reflexive nor transitive, but it is symmetric.

 

Answer:

We have

M = {(2, 3), (3, 2)}

The set, assume S, = {2, 3, 4}

Any relation M on the set S will be defined as M = {(2, 3), (3, 2)}

Thus, (2, 2), (3, 3), (4, 4) \(\notin\) M

Hence we know, M is not reflexive by properties of functions and relations.

We know that,

(2, 3) ɛ M and (3, 2) ɛ M.

Hence we know, M is symmetric by properties of functions and relations.

In this case,

Since, (2, 3) as well as (3, 2) ɛ M

But, (2, 2) \(\notin\) M

Hence we know, M is not transitive by properties of functions and relations.

Therefore we have, M is in this case symmetric, but it is neither reflexive nor transitive.

 

 

Q-7: Prove that the relation M in the set S for all the books in a library of the college BET, the relation given for it is M = {(a, b): a and b have the same number of pages in the book} which is the equivalence relation.

 

Answer:

Let, the set S be the set of all the books in the library of the college BET.

Relation M = {(a, b): a and b have equal number of pages in the book}

M is reflexive by properties of functions and relations as (a, a) ɛ M as x and x will have the equal number of pages in the book.

Let, (a, b) ɛ M

\(\boldsymbol{\Rightarrow }\) a and b have the same/ equal number of pages.

\(\boldsymbol{\Rightarrow }\) b and a will also have the equal number of pages in the book.

\(\boldsymbol{\Rightarrow }\) As, (a, b) ɛ M. So, (b, a) ɛ M

Hence we know, M is symmetric by properties of functions and relations.

Let, (a, b) ɛ M and (b, c) ɛ M

\(\boldsymbol{\Rightarrow }\) Since, a and b have equal number of pages in the book so, b and c will also have the equal number of pages in the book.

\(\boldsymbol{\Rightarrow }\) a and b will also have the equal number of pages.

\(\boldsymbol{\Rightarrow }\) (a, b) ɛ M.

Hence we know, M is transitive by properties of functions and relations.

Thus, M is symmetric, transitive and also, reflexive.

Therefore we have, M is an equivalence relation.

 

 

Q-8: Prove that the relation M of the set S = {2, 3, 4, 5, 6} which is given by M = {(x, y): | x – y | is even}, is an equivalence relation. Also, prove that all the elements are related to each other of the set {3, 5} and the elements of (2, 4, 6} are inter- related with each other. But, elements of {3, 5} and {2, 4, 6} are not related to each other nor their any of the elements are interlinked.

 

Answer:

We have

S = {2, 3, 4, 5, 6, 7} and M = {(x, y): |x – y | is even}

So,

For any of the element x ɛ S, we have | x – x | = 0 and we know that 0 is an even number.

Hence we know, R is reflexive by properties of functions and relations.

Let us assume that, (x, y) ɛ M.

\(\boldsymbol{\Rightarrow }\) | x – y | is even

\(\boldsymbol{\Rightarrow }\) – | -(x – y) | = | y – a | will also be even.

\(\boldsymbol{\Rightarrow }\) (y, x) ɛ M.

Hence we know, M is symmetric.

Assuming, (x, y) ɛ M and (y, z) ɛ M.

\(\boldsymbol{\Rightarrow }\) | x – y | is even and | y – z | is even

\(\boldsymbol{\Rightarrow }\) (x – y) is even and also, (y – z) is even.

\(\boldsymbol{\Rightarrow }\) (x – z) = (x – y) + (y – z) will also be even. [We know that the sum of the two integers is even]

\(\boldsymbol{\Rightarrow }\) | x – y | is even.

\(\boldsymbol{\Rightarrow }\) (x, z) ɛ M

Hence we know, M is transitive by properties of functions and relations.

Therefore we have, M is an equivalence relation.

As per the data, all the elements are related to each other in the set {3, 5} as each of the elements in the set is odd. Therefore we have, the modulus of the difference of any of the two elements will always be even.

Further, all the elements of the set {2, 4, 6} are inter- related as each and every element is an even number in this subset.

And, elements of the subset {3, 5} and {2, 4, 6} are not related to each other in any way as all of the elements of {3, 5} are odd and all the elements of {2, 4, 6} are even. Therefore we have, the modulus of the difference of the elements (for each of the two subsets) won’t be even always, such that 2 – 3, 3 – 4, 2 – 5, 3 – 6, 4 – 3, 4 – 5, 5 – 2, 5 – 4, 5 – 6, 6 – 3 and 6 – 5 all are an odd numbers.

Q-9: Prove that all the relation M of the set S = {a ɛ P : 0 ≤ a ≤ 12}, which is given by

(a) M = {(x, y): | x – y | is a multiple of 3}

(b) M = {(x, y): x = b} is an equivalence relation. Get all the sets of elements which are related to 1 in every case.

 

Answer:

S = {a ɛ P: 2 ≤ a ≤ 14} = {2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14}

(i)

M = {(x, y): | x – y | will be the multiple of 3}

Let, (x, y) ɛ M

\(\boldsymbol{\Rightarrow }\) | x – y | will be the multiple of 3.

\(\boldsymbol{\Rightarrow }\) |- (x – y)| = | y – x | will also be the multiple of 3.

\(\boldsymbol{\Rightarrow }\) (y, x) ɛ M

Hence we know, M is symmetric.

For any of the element x ɛ S, we have (x, x) ɛ M as | x – x | = 0 which is a multiple of 3.

Hence we know, M is reflexive.

Let, (x, y), (y, z) ɛ M

\(\boldsymbol{\Rightarrow }\) | x – y | will be the multiple of 3 and | y – z | will be the multiple of 3.

\(\boldsymbol{\Rightarrow }\) (x – y) will be the multiple of 3 and (y – z) will be the multiple of 3.

\(\boldsymbol{\Rightarrow }\) (x – z) = (x – y) + (y – z) will be the multiple of 3.

\(\boldsymbol{\Rightarrow }\) | x – z | will be the multiple of 3.

\(\boldsymbol{\Rightarrow }\) (x, z) ɛ M

Hence we know, M is transitive by properties of functions and relations.

Therefore we have, M is an equivalence relation.

The set of elements related to 1 is {1, 4, 7, 10, 13} as:

| 1 -1 | = 0 which is a multiple of 0.

| 4 – 1 | = 0 which is a multiple of 3.

| 7 – 1 | = 6 which is a multiple of 3.

| 10 – 1 | = 9 which is a multiple of 3.

| 13 – 1 | = 12 which is a multiple of 3.

 

(b)

M = {(x, y): x = y}

Let, (x, y) ɛ M

\(\boldsymbol{\Rightarrow }\) x = y

\(\boldsymbol{\Rightarrow }\) y = x

\(\boldsymbol{\Rightarrow }\) (y, x) ɛ M

Hence we know, M is symmetric.

For every element x ɛ M, as we have (x, x) ɛ M, as x = x.

Hence we know, M is reflexive.

Let, (x, y) Let, (x, y) ɛ M and (y, z) ɛ M

\(\boldsymbol{\Rightarrow }\) x = y and y = z

\(\boldsymbol{\Rightarrow }\) x = z

\(\boldsymbol{\Rightarrow }\) (x, z) ɛ M

Hence we know, M is transitive.

Therefore we have, M is an equivalence relation.

All the elements in M which are related to 1 can be those elements from the set M which is equal to 1.

Therefore we have, the set of elements related to 1 is {1}.

 

 

Q-10: Give an example for each of the relation, which is

(a) Symmetric but, neither transitive nor reflexive.

(b) Transitive but, neither reflexive nor symmetric.

(c) Symmetric and reflexive but, not transitive.

(d) Transitive and reflexive but, not symmetric.

(e) Transitive and symmetric but, not reflexive.

 

Answer:

(a) Let, S = {7, 8, 9}

A relation M in S as S = {(7, 8), (8, 7)}

The relation M is not reflexive by properties of functions and relations because (7, 7),(8, 8), (9, 9) \(\notin\) M.

(7, 8) ɛ M and also, (8, 7) ɛ M

Hence we know, M is symmetric.

In this case,

(7, 8), (8, 7) ɛ M but, (7, 7) \(\notin\) M

Hence we know, M is not transitive.

Therefore we have, the relation M is symmetric but, neither reflexive nor transitive.

(b) Consider a relation M which is defined as:

M = {(x, y): x < y}

For a ɛ M, we have (x, x) \(\notin\) M as x won’t be less than itself ever.

Also, x = x

Hence we know, M is not reflexive by properties of functions and relations.

As per the given condition, x < y

Let us take an e.g.(2, 3) ɛ M since, 2 < 3.

But, 3 won’t ever be less than 2.

Therefore we have, (3, 2) \(\notin\) M

Hence we know, M is not symmetric by properties of functions and relations.

Let, (x, y), (y, x) ɛ M

\(\boldsymbol{\Rightarrow }\) x < y and y < z

\(\boldsymbol{\Rightarrow }\) x < z

\(\boldsymbol{\Rightarrow }\) (x, z) ɛ M

Hence we know, M is not transitive.

Therefore we have, the relation R is neither symmetric nor it is reflexive but, it is transitive.

 

(c) Let, S = {2, 4, 6}

Let us define the relation M on S as

S = {(2, 2), (4, 4), (6, 6), (2, 4), (4, 2), (4, 6), (6, 4)}

The relation S will be reflexive in this case as for each x ɛ S, (x, x) ɛ M

i.e., {(2, 2), (4, 4), (6, 6)} ɛ M

The relation S will be symmetric in this case as (x, y) ɛ M

\(\boldsymbol{\Rightarrow }\) (y, x) ɛ M for each x, y ɛ M

The relation S won’t be transitive in this case as (2, 4), (4, 6) ɛ M, but (2, 6) \(\notin \) M.

Therefore we have, the relation M is not transitive but, it is symmetric and reflexive.

(d) Defining a relation S in S as,

S = {(x, y): x³ ≥ y³}

(x, x) ɛ M since, x³ = x³

Hence we know, M is reflexive by properties of functions and relations.

(3, 2) ɛ M since, 3³ ≥ 2³

But, (2, 3) \(\notin \) M since, 2³ ≤ 3³

Hence we know, M is not symmetric by properties of functions and relations.

Let, (x, y), (y, z) ɛ M

\(\boldsymbol{\Rightarrow }\) x³ ≥ y³ and y³ ≥ z³

\(\boldsymbol{\Rightarrow }\) x³ ≥ z³

\(\boldsymbol{\Rightarrow }\) (x, z) ɛ M

Hence we know, M is transitive by properties of functions and relations.

Therefore we have, the relation M is not symmetric but, it is transitive and reflexive.

(e) Let, S = {-6, -7}

Let us define a relation M in S as,

S = {(-6, -7), (-7, -6), (-6, -6)}

The relation M is not reflexive by properties of functions and relations as (-7, -7) \(\notin \) M

The relation M is symmetric by properties of functions and relations as (-6, -7) ɛ M and (-7, -6) ɛ M

We can see that,

(-6, -7), (-7, -6) ɛ M and also, (-6, -6) ɛ M

Hence we know, the relation M is transitive tooby properties of functions and relations.

Therefore we have, the relation M is symmetric as well as transitive but, it is not reflexive.

 

 

Q-11: Prove that the relation A in the set S for the points in the plane which is given by A = {(M, N): The distance between the point M from (0, 0) will be the same as the distance between the point N from (0, 0)}, is an equivalence relation. In this case, also prove that the set of all the points which is related to the point M ≠ (0, 0) is a circle which is passing from the point P with having centre at origin.

 

Answer:

A = {(M, N): The distance between the point M from (0, 0) will be the same as the distance between the point N from (0, 0)}

(M, M) ɛ A, as the distance between the point M from (0, 0) will be the same as the distance between the point N from (0, 0).

Hence we know, R is reflexive.

Let, (M, N) ɛ A

\(\boldsymbol{\Rightarrow }\) The distance between the point M from (0, 0) will be the same as the distance between the point N from (0, 0).

\(\boldsymbol{\Rightarrow }\) The distance between the point N from (0, 0) will be the same as the distance between the point M from (0, 0).

\(\boldsymbol{\Rightarrow }\) (N, M) ɛ A

Hence we know, A is symmetric.

Let, (M, N), (N, P) ɛ A

\(\boldsymbol{\Rightarrow }\) The distance between the points M and N from the origin is the same, then also, the distance between the points N and P from the origin is the same.

\(\boldsymbol{\Rightarrow }\) The distance of the points M and P is the same from the origin.

\(\boldsymbol{\Rightarrow }\) (M, P) ɛ A

Hence we know, the relation A is transitive.

Thus, the relation A is an equivalence relation.

The set of all the points which are related to M ≠ (0, 0) can be those points which have the same distance from the origin as the distance of the point M from (0, 0).

Also, If O be the origin and OM = x, then the set of all of the points which are related to the point M is at the distance x from the origin point.

Therefore we have, the set of points hence forms a circle which having the centre at the origin and this circle is passing through the point M.

 

 

Q-12: Prove that the relation A which is defined in the set S for all the triangles as A = {(P₁, P₂): P₁ is similar to P₂}, is an equivalence relation. Assume three right angled triangles, say, triangle P₁ having sides 4, 5, 6, triangle P₂ having sides 6, 14, 15 and triangle P₃ having sides 7, 9, 11. Find which triangle among P₁, P₂ and P₃ will be related?

 

Answer:

M = {(P₁, P₂): P₁ is similar to P₂}

M can be reflexive in this case as, each triangle is similar to itself.

In this case,

If (P₁, P₂) ɛ A, so P₁ is similar to P₂.

\(\boldsymbol{\Rightarrow }\) P₂ is similar to P₁

\(\boldsymbol{\Rightarrow }\) (P₂, P₁₎ ɛ A

Hence we know, M is symmetric.

Let, (P₁, P₂₎, (P₂, P₃) ɛ A

\(\boldsymbol{\Rightarrow }\) P₁ is similar to P₂ and also, P₂ is similar to P₃

\(\boldsymbol{\Rightarrow }\) P₁ is similar to P₃

\(\boldsymbol{\Rightarrow }\) (P₁, P₃) ɛ A

Hence we know, M is transitive.

Therefore we have, R is an equivalence relation.

We can see that,

\(\frac{3}{6} = \frac{4}{8} = \frac{5}{10} \left(\frac{1}{2} \right)\)

Hence we know, the corresponding sides of the triangle P₁ and P₃ are in the same proportion (ratio).

Thus, the triangle P₁ shall be similar to the triangle P₃.

Therefore we have, the triangle P₁ is inter- related to the triangle P₃

 

 

Q-13: Prove that the relation M is defined in the set S of every polygon in such a way that M = {(R₁, R₂): R₁ and R₂ must have the equal number of sides}, is an equivalence relations. Find all the sets of all the elements in S which is related to the right angled triangle T having sides 4, 5 and 6.

Answer:

M = {(R₁, R₂): R₁ and R₂ must have the equal number of sides}

M will be reflexive by properties of functions and relations in this case, as (R₁, R₂) ɛ M, since a same polygon has same number of the sides among itself.

Let, (R₁, R₂) ɛ M

\(\boldsymbol{\Rightarrow }\) R₁ and R₂ has same number of its sides.

\(\boldsymbol{\Rightarrow }\) R₂ and R₁ has same number of its sides.

\(\boldsymbol{\Rightarrow }\) (R₂, R₁) ɛ M

Hence we know, M is symmetric.

Let, (R₁, R₂), (R₂, R₃) ɛ M

\(\boldsymbol{\Rightarrow }\) R₁ and R₂ has same number of its sides.

Also, R₂ and R₃ have same number of its sides.

\(\boldsymbol{\Rightarrow }\) R₁ and R₃ has same number of its sides.

\(\boldsymbol{\Rightarrow }\) (R₁, R₃) ɛ M

Hence we know, M is transitive.

Therefore we have, M will be an equivalence relation by properties of functions and relations.

All the elements in the set S is related to the right angled triangle (T) having sides 4, 5 and 6 are the polygon who have exactly 3 sides.

Therefore we have, all the elements in the set S are related to the right triangle T is the set of all of the triangles.

 

 

Q-14: Assume that, Q is the set of all of the lines in the XY- plane and M is the relation in Q which is defined as M = {(P₁, P₂): P₁ is parallel to P₂}. Prove that the relation M is an equivalence relation. Hence we know, find the set of all of the lines which are related to the line b = 2a + 4.

Answer:

M = {(P₁, P₂): P₁ is parallel to P₂}

M will be reflexive as any line can always be at least parallel to itself, i.e., (P₁, P₁) ɛ M.

Let, (P₁, P₂) ɛ M

\(\boldsymbol{\Rightarrow }\) P₁ is parallel to P₂ and also, P₂ will be parallel to P₁

\(\boldsymbol{\Rightarrow }\) (P₂, P₁) ɛ M

Hence we know, M is symmetric.

Let, (P₁, P₂), (P₂, P₃) ɛ M

\(\boldsymbol{\Rightarrow }\) P₁ is parallel to P₂ and also, P₂ will be parallel to P₃

\(\boldsymbol{\Rightarrow }\) P₁ is parallel to P₃

\(\boldsymbol{\Rightarrow }\) (P₂, P₁) ɛ M

Hence we know, M is transitive by properties of functions and relations.

Therefore we have, M is an equivalence relation.

The set of all of the lines which are related to the given line which is b = 2a + 4 will be the set of all of the lines which are parallel to the line b = 2a + 4.

Here, slope of the given line, say m, b = 2a + 4 is 2.

We know that the slope of the parallel lines is the same.

The line which is parallel to the given line is in the form b = 2a + c, where c ɛ M

Therefore we have, the set of all of the lines which are related to the given line which is given by b = 2a + c, where c ɛ M.

 

 

Q-15: Let, M be the given relation in the set S = {2, 3, 4, 5} which is given by-

M = {(2, 3), (3, 3), (2, 2), (5, 5), (2, 4), (4, 4), (4, 3)}. Select the correct answer:

(a) M is symmetric and reflexive, but it is not transitive.

(b) M is transitive and reflexive, but it is not symmetric.

(c) M is transitive and symmetric, but it is not reflexive.

(d) M is an equivalence relation.

Answer:

Given relation is:

M = {(2, 3), (3, 3), (2, 2), (5, 5), (2, 4), (4, 4), (4, 3)}

We can see that, (x, x) ɛ M, for each x ɛ {2, 3, 4, 5}

Hence we know, M is reflexive by properties of functions and relations.

We can note that, (2, 3) ɛ M, but (3, 2) \(\notin \) M

Hence we know, M is not symmetric by properties of functions and relations.

We can observe that (x, y), (y, z) ɛ M

\(\boldsymbol{\Rightarrow }\) (x, z) ɛ M for each a, b, c ɛ {2, 3, 4, 5}.

Hence we know, M is transitive by properties of functions and relations.

Therefore we have, M is transitive and reflexive, but it is not symmetric.

The correct answer is B.

 

 

Q-16: Let us consider M be a relation in any set M which is given by

M = {(x, y): x = y – 2, y > 6}.

Select the correct choice from the following:

(a) (2, 4) ɛ M (b) (3, 8) ɛ M

(c) (6, 8) ɛ M (d) (8, 7) ɛ M

Answer:

M = {(x, y): x = y – 2, y > 6}

As, y > 6

So, (2, 4) \(\notin \) M

3 ≠ 8 – 2 as well,

So, (3, 8) \(\notin \) M

8 ≠ 7 – 2 as well,

So, (8, 7) \(\notin \) M

Let us consider (6, 8)

6 > 8 and also, we have 6 = 8 – 2

Hence we know,

(6, 8) ɛ M

Therefore we have, the correct answer is C.

 

Definition. A function f : X → Y is defined to be one-one (or injective), if the images of distinct elements of X under f are distinct, i.e., for every x 1 , x 2 ∈ X, f (x1) = f(x2) implies x 1 = x2 . Otherwise, f is called many-one.

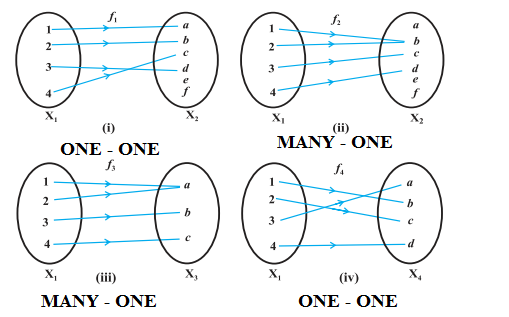
Definition: A function f : X → Y is said to be onto (or surjective), if every element of Y is the image of some element of X under f, i.e., for every y ∈ Y, there exists an element x in X such that f (x) = y. The function f 3 and f 4 in above figure (iii), (iv) are onto and the function f1 in above figure (i) is not onto as elements "e", "f" in X 2 are not the image of any element in X 1 under f 1 .

Definition.

1. f : X → Y is onto if and only if Range of f = Y.

2. A function f : X → Y is said to be one-one and onto (or bijective), if f is both one-one and onto. The function f4 in above figure (iv) is one-one and onto.

Q. Let A be the set of all 50 students of Class X in a school. Let f : A → N be function defined by f (x) = roll number of the student x. Show that f is one-one but not onto.

1. No two different students of the class can have same roll number. Therefore we have, f must be one-one.

2. We can assume without any loss of generality that roll numbers of students are from 1 to 50.

3. This implies that 51 in N is not roll number of any student of the class, so that 51 can not be image of any element of X under f.

4. Hence we know, f is not onto

Q. Show that the function f : N → N, given by f (x) = 2x, is one-one but not onto

1. The function f is one-one, for f (x1) = f (x2) ⇒ 2x1 = 2x2 ⇒ x1 = x2 . Further, f is not onto, as for 1 ∈ N, there does not exist any x in N such that f (x) = 2x = 1.

Q. Prove that the function f : R → R, given by f (x) = 2x, is one-one and onto.

1. f is one-one, as f(x1) = f(x2) = 2x1 = 2x2 = x1 = x2

2. Also, given any real number y in R, there exists y/2 in R such that

3. f(y/2) = 2(y/2) = y

4. Hence we know, f is onto.

Q. Show that the function f : N → N, given by f (1) = f (2) = 1 and f (x) = x – 1, for every x > 2, is onto but not one-one.

1. f is not one-one, as f (1) = f (2) = 1

2. But f is onto, as given any y ∈ N, y ≠ 1, we can choose x as y + 1 such that f (y + 1) = y + 1 – 1 = y.

3. Also for 1 ∈ N, we have f (1) = 1.

Q. Show that the function f : R → R, defined as f (x) = x² , is neither one-one nor onto

1. Since f (– 1) = 1 = f (1), f is not one- 2 one.

2. Also, the element – 2 in the co-domain R is not image of any element x in the domain R (Why?).

3. Therefore we have f is not onto.

Q. Show that an onto function f : {1, 2, 3} → {1, 2, 3} is always one-one.

1. Suppose f is not one-one. Then there exists two elements, say 1 and 2 in the domain whose image in the co-domain is same.

2. Also, the image of 3 under f can be only one element.

3. Therefore we have, the range set can have at the most two elements of the co-domain {1, 2, 3}, showing that f is not onto, a contradiction. Hence we know, f must be one-one.

Q. Show that a one-one function f : {1, 2, 3} → {1, 2, 3} must be onto.

1. Since f is one-one, three elements of {1, 2, 3} must be taken to 3 different elements of the co-domain {1, 2, 3} under f. Hence we know, f has to be onto.

 

EXERCISE – 1. 2

 

 

Q-1: Prove that the function f: \(R_{*}\rightarrow R_{*}\) which is defined by f(a) = \(\frac{1}{a}\) which is one- one and onto, where \(R_{*}\) is the set of all of the non- zero real numbers. Check whether the result is true or not, if the domain, say, \(R_{*}\) is replaced by M having co- domain as same as \(R_{*}\)?

Answer:

As per the data given in the question,

\(R_{*}\rightarrow R_{*}\) which is defined by f(a) = \(\frac{1}{a}\)

For one- one condition:

Let, a and b \(\epsilon R_{*} \) such that, f(a) = f(b)

\(\Rightarrow \frac{1}{a} = \frac{1}{b}\)

\(\boldsymbol{\Rightarrow }\) a = b

Hence we know, the function f is one- one.

For onto condition:

Clearly, for b\(\epsilon R_{*} \), there must exists a = \(\frac{1}{b} \; \epsilon R_{*} \) [since, b ≠ 0], so that

f(x) = \(\frac{1}{\frac{1}{b}}\) = y

Hence we know, the function f is onto.

Therefore we have, the given function f(a) is one- one as well as onto.

Let us consider a another function g: M → \( R_{*} \) which is defined by g(a) = \(\frac{1}{a}\).

g(x₁) = g(x₂)

\(\Rightarrow \frac{1}{a_{1}} = \frac{1}{a_{2}}\)

\(\boldsymbol{\Rightarrow }\) x₁ = x₂

Hence we know, the another function g is also one- one.

It is obvious that g is not onto as for 1.2 \(\epsilon R_{*} \), there doesn’t exist any a in M so that:

g(a) = \(\frac{1}{1.2}\)

Therefore we have, the function ‘g’ is one- one but, it is not onto.

 

 

Q-2: Check the following functions for their injectivity and surjectivity:

(i) f: N →N which is given by f(a) = a²

(ii) f: Z →Z which is given by f(a) = a²

(iii) f: R → R which is given by f(a) = a²

(iv) f: N →N which is given by f(a) = a³

(v) f: Z → Z which is given by f(a) = a³

Answer:

(i) f: N → N which is given by f(a) = a²

We can see that for a, b ɛ N

f(a) = f(y)

\(\boldsymbol{\Rightarrow }\) a² = b²

\(\boldsymbol{\Rightarrow }\) a = b

Hence we know, the function f is injective.

2 ɛ N

But, there doesn’t exist any of the a in N, so that f(a) = b² = 2

Hence we know, the function f is not surjective.

Therefore we have, the function f is not surjective but, it is injective.

 

(ii) f: Z → Z which is given by f(a) = a²

We can see that for a, b ɛ Z

f(-1) = f(1) = 1

But, -1≠ 1.

Hence we know, the function f is not injective.

-2 ɛ Z

But, there doesn’t exist any of the a ɛ Z, so that f(a) = – 2 or a² = -2

Hence we know, the function f is not surjective.

Therefore we have, the function f is neither surjective nor it is injective.

 

(iii) f: R → R which is given by f(a) = a²

We can see that for a, b ɛ R

f(-1) = f(1) = 1

But, -1≠ 1.

Hence we know, the function f is not injective.

-2 ɛ R

But, there doesn’t exist any of the a ɛ R, so that f(a) = – 2 or a² = -2

Hence we know, the function f is not surjective.

Therefore we have, the function f is neither surjective nor it is injective.

 

(iv) f: N → N which is given by f(a) = a³

We can see that for a, b ɛ N

f(a) = f(y)

\(\boldsymbol{\Rightarrow }\) a³ = b³

\(\boldsymbol{\Rightarrow }\) a = b

Hence we know, the function f is injective.

2 ɛ N

But, there doesn’t exist any of the element of a ɛ Z, so that f(a) = 2 or a³ = 2

Hence we know, the function f is not surjective.

Therefore we have, the function f is not surjective but it is injective.

 

(v) f: Z → Z which is given by f(a) = a³

We can see that for a, b ɛ Z

f(a) = f(y)

\(\boldsymbol{\Rightarrow }\) a³ = b³

\(\boldsymbol{\Rightarrow }\) a = b

Hence we know, the function f is injective.

2 ɛ Z

But, there doesn’t exist any of the element of a ɛ Z, so that f(a) = 2 or a³ = 2

Hence we know, the function f is not surjective.

Therefore we have, the function f is not surjective but it is injective.

 

 

Q-3: Show that the GIF (Greatest Integer Function) f: R →R which is given by f(a) = [a], which is neither one- one nor onto, where [a] notifies the greatest integer which must be less than or equal to a.

Answer:

f: R → R which is given by f(a) = [a]

f(1.4) = [1.4] = 1, f(1.7) = [1.7] = 1

\(\boldsymbol{\Rightarrow }\) f(1.4) = f(1.7) = 1, but 1.4 ≠ 1.7

Hence we know, the function f is not one- one.

Let us consider that, 0.9 ɛ R.

We know that, f(a) = [a] will always be any integer.

So, there doesn’t exist any of the element a ɛ R, such that f(a) = 0.9

Hence we know, the function f is not onto.

Therefore we have, the GIF (Greatest Integer Function) is neither onto nor one- one.

 

 

Q-4: Prove that the Modulus Function f: R → R which is given by f(a) = [a], which is neither one- one nor it is onto, where |a| is a, if a will be positive or 0 and |a| is –a, if a will be negative.

Answer:

f : R → R which is given by

f(a) = |a| = a, if a ≥ 0 and (-a), if a ≤ 0

It is obvious that f(-2) = |-2| = 2 and f(2) = |2| = 2

So, f(-2) = f(2), but -2 ≠ 2

Hence we know, f is not one- one

Let us consider -2 ɛ R.

We know that, f (a) = |a| will always be non- negative.

Therefore we have, neither of any element a exist in the domain R, so that

f(a) = |a| = -2.

Hence we know, f is not onto.

Hence we know, the modulus function is neither onto nor one- one.

 

 

Q-5: Prove that the Signum function f: R → R which is given by f(a) =

1, if a > 0

0, if a = 0

-1, if x < 0 is neither onto nor one- one.

Answer:

f: R → R which is given by f(a) =

1, if a > 0

0, if a = 0

-1, if x < 0

Since, f(a) can only take 3 values (i.e., 1, 0, -1) for the elements -3 in the co- domain R, there does not exist any of the a in domain R, so that f(a) = -3.

Hence we know, f is not onto.

Here, we can see that:

f(2) = f(3) = 1, but 2 ≠ 3

Hence we know, f is not one- one.

Therefore we have, the Signum function in this case is neither onto nor one- one.

 

 

Q-6: Let us take P as {2, 3, 4}, Q as {5, 6, 7, 8} and let f = {(2, 5), (3, 6), (4, 7)} which are the function from P and Q. Prove that the function f is one- one.

Answer:

As per the data we have

P = {2, 3, 4} and Q = {5, 6, 7, 8}

f : P → Q is defines as f = {(2, 5), (3, 6), (4, 7)}

Thus, f (2) = 5, f(3) = 6 and f(4) = 7

In this case,

Here the images of the distinct elements of P under f are also distinct.

Therefore we have, the function f is not one- one.

Q-7. Check whether the function in each of the following conditions is one- one, onto or bijective. Justify your answer in each cases.

(i) f : R → R which is defines by f(a) = 4 – 5a

(ii) f : R → R which is defined by f(a) = 2 + a²

Answer:

(i) f : R → R which is defined as f(a) = 4 – 5a

Let, a₁, a₂ ɛ so that, f(a₁) = f(a₂)

\(\boldsymbol{\Rightarrow }\) 4 – 5a₁ = 4 – 5a₂

\(\boldsymbol{\Rightarrow }\) – 5a₁ = – 5a₂

\(\boldsymbol{\Rightarrow }\) a₁ = a₂

Hence we know, the function f is one- one.

In this case,

For any of the real number (b) in R, there exists \(\frac{4 – b}{5}\) in R, so that

f (\(\frac{4 – b}{5}\)) = \( 4 – 5\left(\frac{4 – b}{5} \right) \)

f (\(\frac{4 – b}{5}\)) = 4 – (4 – b)

f (\(\frac{4 – b}{5}\)) = b

Hence we know, the function f is onto.

Therefore we have, the function f is bijective.

 

(ii) f : R → R which is defined as f(a) = 2 + a²

Let, a₁, a₂ ɛ so that, f(a₁) = f(a₂)

\(\boldsymbol{\Rightarrow }\) 2 + a₁² = 2 + a₂²

\(\boldsymbol{\Rightarrow }\) a₁² = a₂²

\(\boldsymbol{\Rightarrow }\) a₁ = ± a₂

Thus, f(a₁) = f(a₂) which doesn’t imply that a₁ = a₂

For example, f(2) = f(-2) = 3

Hence we know, the function f is not one- one.

In this case,

Take an element -3 in the co- domain R.

We can see that, f(a) = 2 + a² which is positive for all of the x ɛ R.

So, there doesn’t exist any a in the domain R so that f(a) = -3.

Hence we know, the function f is not onto.

Therefore we have, the function f is neither one- one nor onto so, it is not bijective.

 

 

Q-8: Let us consider P and Q be the two sets. Prove that f : P × Q → Q × P so that (x, y) = (y, x) is bijective function.

Answer:

f : P × Q → Q × P which is defined as f(x, y) = y, x.

Let, (x₁, y₁₎, (x₂, y₂₎ ɛ P × Q so that, f(x₁, y₁₎= f(x₂, y₂₎

\(\boldsymbol{\Rightarrow }\) (y₁, x₁₎ = (y₂, x₂₎

\(\boldsymbol{\Rightarrow }\) y₁ = y₂ and x₁ = x₂

\(\boldsymbol{\Rightarrow }\) (x₁, y₁₎ = (x₂, y₂₎

Hence we know, the function f is one- one.

Let us consider that (y, x) ɛ Q × P be any element.

Thus,

There will exist (x, y) ɛ P × Q so that,

f(x, y) = (y, x).

Hence we know, f is onto.

Therefore we have, the function f is bijective by properties of functions and relations.

 

 

Q-9: Let f : N → N which will be defined by f(p) =

\( \frac{p + 1}{2}\), if p is odd

\( \frac{p}{2}\), if p is even, for all p ɛ N.

Check and justify your answer that whether the function f is bijective or not?

Answer:

f : N → N which is defined as f(p) =

\(\frac{p + 1}{2}\), if p is odd

\(\frac{p}{2}\), if p is even

for all n ɛ N

We can see that:

f(3) = \(\frac{3 + 1}{2}\) = 2 and f(4) = \(\frac{4}{2}\) = 2

\(\boldsymbol{\Rightarrow }\) f(3) = f(4), but 3 ≠ 4

Hence we know, f is not one- one.

Let us consider any natural number (p) in the co- domain N.

Case-1: [ p is odd ]

\(\boldsymbol{\Rightarrow }\) p = 2r + 1 for few r ɛ N.

Thus, there exists 4r + 1 ɛ N so that,

f(4r + 1) = \(\frac{4r + 1 + 1}{2}\) = \(\frac{4r + 2}{2}\) = 2r + 1

Case-2: [p is even]

\(\boldsymbol{\Rightarrow }\) p = 2r for few r ɛ N.

Thus, there exists 4r ɛ N so that,

f(4r) = \(\frac{4r}{2}\) = 2r

Hence we know, the function f is onto.

Therefore we have, the function f is not a bijective function by properties of functions and relations.

 

 

Q-10: Let P = A – {3} and Q = A – {1}. Let us consider the function f : P → Q which defined by f(a) = \(\left(\frac{a – 3}{a – 4} \right)\). Check and Justify your answer, whether the function f is onto and one- one?

Answer:

P = A – {3}, Q = A – {1} and f : P → Q which is defined by

f(a) = \(\left(\frac{a – 3}{a – 4} \right)\)

Let, a, b ɛ P so that f(a) = f(b)

\(\boldsymbol{\Rightarrow }\) \( \frac{a – 3}{a – 4} = \frac{b – 3}{b – 4} \)

\(\boldsymbol{\Rightarrow }\) (a – 3)(b – 4) = (b – 3)(a – 4)

\(\boldsymbol{\Rightarrow }\) ab – 4a – 3b + 12 = ab – 4b – 3a + 12

\(\boldsymbol{\Rightarrow }\) a = b

Hence we know, the function f is one- one.

Let, b ɛ Q = A – {1}.

Thus, b ≠ 1

Then, the function f will be onto if a ɛ P so that, f(a) = b.

f(a) = b

\(\boldsymbol{\Rightarrow }\) \(\frac{a – 3}{a – 4}\) = b

\(\boldsymbol{\Rightarrow }\) (a – 3) = b(a – 4)

\(\boldsymbol{\Rightarrow }\) a – 3 = ab – 4b

\(\boldsymbol{\Rightarrow }\) a(1 – b) = 3 – 4b

\(\boldsymbol{\Rightarrow }\) a = \(\frac{3 – 4b}{1 – b}\) ɛ [b ≠ 1]

Then,

For any value of b ɛ Q, there will exist \(\frac{3 – 4b}{1 – b}\) ɛ P, so that

f(\(\frac{3 – 4b}{1 – b}\)) = \(\frac{\left (\frac{3 – 4b}{1 – b} \right) – 3}{\left (\frac{3 – 4b}{1 – b} \right) – 4}\)

= \(\frac{\left(3 – 4b \right) – 3\left(1 – b \right)}{\left(3 – 4b \right) – 4\left(1 – b \right)}\)

= \(\frac{3 – 4b – 3 + 3b}{3 – 4b – 4 + 4b}\)

= \(\frac{-b}{-1}\) = b

Hence we know, the function f is onto.

Therefore we have, the function f is onto as well as it is one- one.

 

 

Q-11: Let us assume, f : R → R will be defined as g(a) = a⁵. Select the correct answer from the following:

(a) f is many- one onto (b) f is one- one onto

(c) f is neither one- one nor onto (d) f is one- one but, not onto

Answer:

f : R → R which is defined as g(a) = a⁴.

Let, a, b ɛ R so that f(a) = f(b).

\(\boldsymbol{\Rightarrow }\) a⁴ = b⁴

\(\boldsymbol{\Rightarrow }\) a = ± b

Thus, f(a) = f(b) doesn’t imply a = b.

Example:

f(3) = f(-3) = 3

Hence we know, the function f is not one- one.

Consider an element 3 in the co- domain R. It’s obvious that there doesn’t exist any a in the domain R so that, f(a) = 3.

Hence we know, the function f is not onto.

Therefore we have, the function f is neither one- one nor it is onto by properties of functions and relations.

Thus, the correct answer is option (c).

 

 

Q-12: Let us assume, f : R → R will be defined as g(a) = 4a . Select the correct answer from the following:

(a) f is many- one onto (b) f is one- one onto

(c) f is neither one- one nor onto (d) f is one- one but, not onto

Answer:

f : R → R which is defined as g(a) = 4a.

Let, a, b ɛ R so that f(a) = f(b).

\(\boldsymbol{\Rightarrow }\) 4a = 4b

\(\boldsymbol{\Rightarrow }\) a = b

Hence we know, the function f is one- one.

For any of the real number (b) in the co- domain R, there must exist \(\frac{b}{3}\) in R so that, f(\(\frac{b}{3} = 3\left(\frac{b}{3} \right) = y \))

Hence we know, the function f is onto.

Therefore we have, the function f is one- one and also, it is onto by properties of functions and relations.

Thus, the correct answer is option (b).

 

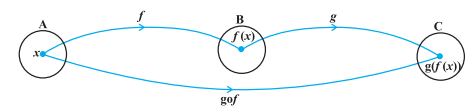
Definition Let f : A → B and g : B → C be two functions. Then the composition of f and g, denoted by gof, is defined as the function gof : A → C given by gof (x) = g(f (x)), ∀ x ∈ A.

Q. Let f : {2, 3, 4, 5} → {3, 4, 5, 9} and g : {3, 4, 5, 9} → {7, 11, 15} be functions defined as f (2) = 3, f (3) = 4, f (4) = f (5) = 5 and g (3) = g (4) = 7 and g (5) = g (9) = 11. Find gof.

1. We have gof (2) = g (f (2)) = g (3) = 7, gof (3) = g (f (3)) = g (4) = 7, gof (4) = g (f (4)) = g (5) = 11 and gof (5) = g (5) = 11

Q. Find gof and fog, if f : R → R and g : R → R are given by f (x) = cos x and g (x) = 3x² . Show that gof ≠ fog.

1. We have gof (x) = g (f (x)) = g (cos x) = 3 (cos x)² = 3 cos² x.

2. Similarly, fog(x) = f (g (x)) = f (3x²) = cos (3x²). Note that 3cos² x ≠ cos 3x², for x = 0. Hence we know, gof ≠ fog.

Q. Show that if f : A → B and g : B → C are one-one, then gof : A → C is also one-one.

1. Suppose gof (x₁) = gof (x₂)

2. g (f (x₁)) = g(f (x₂))

3. f (x₁) = f (x₂), as g is one-one

4. x₁ = x₂, as f is one-one. Hence we know, gof is one-one.

Q. Show that if f : A → B and g : B → C are onto, then gof : A → C is also onto.

1. Given an arbitrary element z ∈ C, there exists a pre-image y of z under g such that g (y) = z, since g is onto. Further, for y ∈ B, there exists an element x in A

2. with f (x) = y, since f is onto. Therefore we have, gof (x) = g (f (x)) = g (y) = z, showing that gof is onto.

Q. Consider functions f and g such that composite gof is defined and is oneone. Are f and g both necessarily one-one.

1. Consider f : {1, 2, 3, 4} → {1, 2, 3, 4, 5, 6} defined as f (x) = x, ∀ x and g : {1, 2, 3, 4, 5, 6} → {1, 2, 3, 4, 5, 6} as g (x) = x, for x = 1, 2, 3, 4 and g (5) = g (6) = 5.

2. Then, gof (x) = x ∀ x, which shows that gof is one-one. But g is clearly not one-one.

Q. Are f and g both necessarily onto, if gof is onto?

1. Consider f : {1, 2, 3, 4} → {1, 2, 3, 4} and g : {1, 2, 3, 4} → {1, 2, 3} defined as f (1) = 1, f (2) = 2, f (3) = f (4) = 3, g (1) = 1, g (2) = 2 and g (3) = g (4) = 3

2. It can be seen that gof is onto but f is not onto.

Q. Let f : {1, 2, 3} → {a, b, c} be one-one and onto function given by f (1) = a, f (2) = b and f (3) = c. Show that there exists a function g : {a, b, c} → {1, 2, 3} such that gof = I_X and fog = I_Y, where, X = {1, 2, 3} and Y = {a, b, c}.

1. Consider g : {a, b, c} → {1, 2, 3} as g (a) = 1, g (b) = 2 and g (c) = 3.

2. It is easy to verify that the composite gof = I_X is the identity function on X and the composite fog = I_Y is the identity function on Y.

Q. Consider f : N → N, g : N → N and h : N → R defined as f (x) = 2x, g (y) = 3y + 4 and h (z) = sin z, ∀ x, y and z in N. Show that ho(gof ) = (hog)of.

1. ho(gof) (x) = h(gof (x)) = h(g(f (x))) = h(g (2x))

2. = h(3(2x) + 4) = h(6x + 4) = sin (6x + 4); ∀ x ∈ N

3. Also, ((hog)of ) (x)=(hog) ( f (x)) = (hog) (2x) = h ( g (2x))

4. = h(3(2x) + 4) = h(6x + 4) = sin (6x + 4), ∀ x ∈

5. This shows that ho(gof) = (hog)of. This result is true in general situation as well

EXERCISE – 1.3

Q-1: Let us consider, g : {3, 5, 6} → {2, 4, 7} and f : {2, 4, 7} → {3, 5} will begiven by g = {(3, 4), (5, 7), (6, 3)} and f = {(3, 5), (4, 5), (7, 3)}. Find fog.

Answer:

The given functions g : {3, 5, 6} → {2, 4, 7} and f : {2, 4, 7} → {3, 5} will be defined by g = {(3, 4), (5, 7), (6, 3)} and f = {(3, 5), (4, 5), (7, 3)}

fog(3) = f[g(3)] = f(4) = 5 [as, g(3) = 4 and f(4) = 5]

fog(5) = f[g(5)] = f(7) = 3 [as, g(5) = 7 and f(7) = 3]

fog(6) = f[g(6)] = f(3) = 5 [as, g(6) = 3 and f(3) = 5]

Hence we know,

fog = {(3, 5), (5, 3), (6, 5)}

 

 

Q-2: Let us consider

f, g and h be the functions from R to R. Prove that:

(g + f)oh = goh + foh

(g.f)oh = (goh).(foh)

Answer:

We need to prove that,

(g + f)oh = foh + goh

\(\boldsymbol{\Rightarrow }\) {(g + f)oh}(x) = {goh + foh}(x)

In this case,

LHS = {(g + f)oh}(x)

= (g + f)[h(x)]

= g[h(x)] + f[h(x)]

= (goh)(x) + (foh)(x)

= {(goh) + (foh)}{x)

= RHS

Therefore we have, {(g + f)oh} = goh + foh

Hence we know, proved.

We need to prove:

(g.f)oh = (goh).(foh)

LHS = [(g.f)oh](x)

= (g.f)[h(x)]

= g[h(x)]. f[h(x)]

= (goh)(x) . (foh)(x)

= {(goh).(foh)}(x)

= (goh).(foh)

Hence we know, LHS = RHS

Therefore we have, (g.f)oh = (goh).(foh)

 

 

Q-3: Find fog and gof, if

(i) g(a) = |a| and f(a) = |5a – 2|

(ii) g(a) = 8a³ and f(a) = \(x^{\frac{1}{3}}\)

 

Answer:

(i) g(a) = |a| and f(a) = |5a – 2|

Therefore we have, the binary operation * is not associative.

fog(a) = f(g(a)) = f(|a|) = \(\left | 5\left | x \right | – 2 \right |\)

Therefore we have, gof(a) = g(f(a)) = g(|5x – 2|) = \(\left |\left | 5x – 2 \right | \right |\) = \( \left | 5x – 2 \right | \)

(ii) g(a) = 8a³ and f(a) = a^{\(\frac{1}{3}\)}

Therefore we have, fog(a) = f(g(a)) = f(8a³) = (8a³)^{\(\frac{1}{3}\)} = (2³ a³) ^{\(\frac{1}{3}\)} = 2a

Therefore we have, gof(a) = g(f(a)) = g(\(a^{\frac{1}{3}}\)) = 8(\(a^{\frac{1}{3}}\))³ = 8a

 

 

Q-4: If g(a) = \(\frac{\left(4a + 3 \right)}{\left(6a – 4 \right)}\), a ≠ \(\frac{2}{3} \). Prove that gog(a) = a, for every a ≠ \(\frac{2}{3} \). What will be the inverse of the function g?

 

Answer:

As per the data given in the question, we have

g(a) = \(\frac{4a + 3}{6a – 4}\), a ≠ \(\frac{2}{3} \)

(gog)(x) = g(g(x)) = g(\(\frac{4a + 3}{6a – 4}\)) = \(\frac{4\left (\frac{4a + 3}{6a – 4} \right) + 3}{6 \left (\frac{4a + 3}{6a – 4} \right) – 4}\)

= \(\frac{16a + 12 + 18a – 12}{24a + 18 – 24a + 16} \)

= \(\frac{34a}{34}\)

Therefore we have, gog(a) = a, for all of the a ≠ \(\frac{2}{3} \)

So, gog = I_a

Therefore we have, the function f given is invertible and the inverse of the function f is f itself by properties of functions and relations.

 

Q-5: Explain with suitable reason that, whether the following functions has any inverse

(i) g : {2, 3, 4, 5} → {11} with

g = {(2, 11), (3, 11), (4, 11), (5, 11)}

(ii) f : {6, 7, 8, 9} → {2, 3, 4, 5} with

f = {(6, 5), (7, 4), (8, 5), (9, 3)}

(iii) h : {3, 4, 5, 6} → {8, 10, 12, 14} with

h = {(3, 8), (4, 10), (5, 12), (6, 14)}

Answer:

(i) g : {2, 3, 4, 5} → {11} which is defined as g = {(2, 11), (3, 11), (4, 11), (5, 11)}

From the definition of f, given in the question, we note that, the function f is a many one function as,

g(2) = g(3) = g(4) = g(5) = 11

Hence we know, the function g is not one- one.

Therefore we have, in this case, the function g doesn’t have any inverse.

 

(ii) f : {6, 7, 8, 9} → {2, 3, 4, 5} which is defined as f = {(6, 5), (7, 4), (8, 5), (9, 3)}

From the definition of f, given in the question, we note that, the function f is a many one function as,

f(6) = f(7) = 4

Hence we know, the function f is not one- one.

Therefore we have, in this case, the function f doesn’t have any inverse.

 

(iii) h : {3, 4, 5, 6} → {8, 10, 12, 14} which is defined as

h = {(3, 8), (4, 10), (5, 12), (6, 14)}

Here, all the distinct elements from the set {3, 4, 5, 6} have distinct images under h.

Hence we know, the function h is one- one.

Also, the function h is onto as each element y from the set {8, 10, 12, 14}, there exists an element, say a, in the set {3, 4, 5, 6} so that h(a) = b.

Hence we know, h is one- one as well as onto function.

Therefore we have, the function h will have an inverse.

 

 

Q-6: Prove that:

g : [-2, 2] → R,

which is given by g(a) = \(\frac{a}{\left(a + 2 \right)}\) will be one- one. What will be the inverse of the function g : [-2, 2] → Range g.

Answer:

g : [-2, 2] → R which is given by

g(a) = \(\frac{a}{\left(a + 2 \right)}\)

For one- one:

Let, g(a) = g(b)

\(\boldsymbol{\Rightarrow }\) \(\frac{a}{\left(a + 2 \right)}\) = \(\frac{b}{\left(b + 2 \right)}\)

\(\boldsymbol{\Rightarrow }\) a(b + 2) = b (a + 2)

\(\boldsymbol{\Rightarrow }\) ab + 2a = ab + 2b

\(\boldsymbol{\Rightarrow }\) 2a = 2b

\(\boldsymbol{\Rightarrow }\) a = b

Hence we know, the function g is one- one function.

We can see that, g : [-2, 2] → Range g is onto.

Hence we know, g : [-2, 2] → Range g here is one- one and onto, and thus, the inverse of the function f : [-2, 2] → Range g exists.

Let us consider f : Range g → [-2, 2] be the inverse for g.

Let, b be any arbitrary element of the range f.

As, f : [-2, 2] → Range g is onto, here we have

b = g(a) for some values of a ɛ [-2, 2]

\(\boldsymbol{\Rightarrow }\) b = \(\frac{a}{\left(a + 2 \right)}\)

\(\boldsymbol{\Rightarrow }\) b(a + 2) = a

\(\boldsymbol{\Rightarrow }\) ab + 2b = a

\(\boldsymbol{\Rightarrow }\) a(1 – b) = 2b

\(\boldsymbol{\Rightarrow }\) a = \(\frac{2b}{\left(1 – b \right)}\), b ≠ 1

Then,

Let we define f: Range g → [-2, 2] as

f(b) = \(\frac{2b}{\left(1 – b \right)}\), b ≠ 1

Thus,

(fog)(a) = f(g(a)) = f\(\left(\frac{a}{a + 2} \right)\)= \(\frac{2\left (\frac{a}{a + 2} \right)}{1 – \left (\frac{a}{a + 2} \right)} = \frac{2a}{a + 2 – a} = \frac{2a}{2} = a\)

and,

(gof)(a) = g(f(a)) = g \(\left (\frac{2b}{1 – b} \right) = \frac{\left (\frac{2b}{1 – b} \right)}{\left (\frac{2b}{1 – b} \right) + 2} = \frac{2b}{2b + 2 – 2b} = \frac{2b}{2} = b\)

Hence we know,

fog = a = \(I_{\left \lfloor -1, 1 \; \right \rfloor}\) and gof = b = I_Range f

Thus,

g^-1 = f

g^-1(b) = \( \frac{2b}{2}\), b ≠ 1.

 

 

Q-7: Let us consider g : R → R which is given by g(a) = 4a + 3. Prove that the function g is invertible. Also find the inverse of g.

Answer:

g : R → R which is given by,

g(a) = 4a + 3

For one- one function,

Let, g(a) = g(b)

\(\boldsymbol{\Rightarrow }\) 4a + 3 = 4b + 3

\(\boldsymbol{\Rightarrow }\) 4a = 4b

\(\boldsymbol{\Rightarrow }\) a = b

Hence we know, the function g is a one- one function.

For onto function,

For b ɛ R, let b = 4a + 3.

\(\boldsymbol{\Rightarrow }\) a = \(\frac{b – 3}{4}\) ɛ R.

Hence we know, for every b ɛ R, there does exist a = \(\frac{b – 3}{4}\) ɛ R, so that

g(a) = g \(\left (\frac{b – 3}{4} \right)\) = 4 \(\left (\frac{b – 3}{4} \right)\) + 3 = b

Hence we know, the function g is onto.

Therefore we have, the function g is one- one and onto and hence, g^-1 will exist.

Let us consider, f: R → R by f(x) = \(\frac{b – 3}{4}\)

Then,

(fog)(a) = f(g(a)) = f(4a + 3) = \(\frac{\left (4a + 3 \right) – 3}{4} = \frac{4x}{4} = x\)

And,

(gof)(b) = g(f(x)) = g\(g\left (\frac{b – 3}{4} \right) = 4\left (\frac{b – 3}{4} \right) + 3 = b – 3 + 3 = b\)

So, fog = gof = I_R

Therefore we have, the function f will be invertible and have inverse which is given by g^-1(b) = f(b) = \(\frac{b – 3}{4}\)

 

 

Q-8: Let us consider a function, g : R₊ → [4, ) which is given by g(a) = a² + 4. Prove that the function g is invertible with the inverse g^-1 of the given function g by g^-1 (b) = \(\sqrt{b – 4}\), where R₊ will be the set of all the non- negative real number.

Answer:

g : R₊ → [4, ∞) which is given by g(a) = a² + 4

For one- one function,

Let, g(a) = g(b)

\(\boldsymbol{\Rightarrow }\) a² + 4 = b² + 4

\(\boldsymbol{\Rightarrow }\) a² = b²

\(\boldsymbol{\Rightarrow }\) a = b

Hence we know, the function f is one- one function.

For onto function,

For b ɛ [4, ∞), let b = a² + 4

\(\boldsymbol{\Rightarrow }\) a² = b – 4 ≥ 0

\(\boldsymbol{\Rightarrow }\) a = \(\sqrt{b – 4}\) ≥ 0

Hence we know, for every b ɛ [4, ∞), there exists a = \(\sqrt{b – 4}\) ɛ R₊, so that

G(a) = g(\(\sqrt{b – 4}\)) = (\(\sqrt{b – 4}\))² + 4 = b – 4 + 4 = b

Hence we know, the function g is onto.

So, the function g is one- one and onto and hence, g^-1 exists.

Let we define, f : [4, ∞) → R₊ by f(b) = \(\sqrt{b – 4}\)

Then,

(fog)(a) = f(g(a)) = f(\(x^{2} + 4\)) = \(\sqrt{\left (a^{2} + 4 \right) – 4} = \sqrt{a^{2}}\) = a

And,

(gof)(b) = g(f(b)) = g\(\left (\sqrt{b – 4} \right)\) = \(\left (\sqrt{b – 4} \right)^{2}\) + 4 = b – 4 + 4 = b

Hence we know, gof = fog = I_R

Therefore we have, the function g is invertible and it will be the inverse of g which is given by g^-1(b) = f(b) = \(\sqrt{b – 4}\)

Q-9: Let us consider a function, g: R₊ → [-5, ∞) which is given by g(a) = 9a² + 6a – 5. Prove that, the function g is invertible with g^-1(b) = \(\left (\frac{\left (\sqrt{b + 6} \right) – 1}{3} \right)\).

Answer:

g: R₊ → [-5, ∞) which is given by g(a) = \(9a^{2} + 6a – 5 \)

Let, b be an arbitrary element of [-5, ∞)

Let,

b = \(9a^{2} + 6a – 5 \)

\(\boldsymbol{\Rightarrow }\) b = (3a + 1)² – 1 – 5 = (3a + 1)² – 6

\(\boldsymbol{\Rightarrow }\) b + 6 = (3a + 1)²

\(\boldsymbol{\Rightarrow }\) 3a + 1 = \(\sqrt{b + 6}\) [as b ≥ -5 \(\boldsymbol{\Rightarrow }\) b + 6 > 0]

\(\boldsymbol{\Rightarrow }\) a = \(\frac{\left (\sqrt{b + 6} \right) – 1}{3}\)

Hence we know, the function g is onto, which means having range g = [-5, ∞)

Let us consider, f : [-5, ∞) → R₊ as f(b) = \(\frac{\left (\sqrt{b + 6} \right) – 1}{3}\)

Then,

(fog)(a) = f(g(a)) = f(9a² + 6a – 5) = g ((3a + 1)² – 6) = \(\frac{\sqrt{\left (3a + 1 \right)^{2} – 6 + 6} – 1}{3}\)

=\(\frac{3a + 1 – 1}{3}\) = \(\frac{3a}{3}\) = a

And,

(gof)(b) = g(f(b)) = g\(\left (\frac{\sqrt{b + 6} – 1}{3} \right) = \left [3 \left (\frac{\sqrt{b + 6} – 1}{3} \right) + 1 \right]^{2} – 6\)

= \(\left (\sqrt{b + 6} \right)^{2} – 6\) = b + 6 – 6 = b

Hence we know, fog = a = I_R and gof = b = I_Range g

Therefore we have, g is invertible and the inverse of g will be given by:

g^-1(b) = f(b) = \(\left (\frac{\left (\sqrt{y + 6} \right)^{2} – 1}{3} \right)\)

 

 

Q-10: Let us consider a function g : P → Q be an invertible function. Prove that the function g have a unique inverse.

Answer:

Let, the function, g : P → Q be an invertible function.

Let, function g have two inverses (say, g₁ and g₂)

Thus, for every b ɛ Q, we have,

gof₁ (b) = I_Y(b) = gof₂(b)

\(\boldsymbol{\Rightarrow }\) g(f₁(b)) = g(f₂(b))

\(\boldsymbol{\Rightarrow }\) f₁(b) = f₂(b) [as g is invertible \(\boldsymbol{\Rightarrow }\) g is on- one]

\(\boldsymbol{\Rightarrow }\) f₁= f₂ [as f is one- one]

Therefore we have, the function g has a unique inverse.

Q-11. Let us consider the function g: {2, 3, 4} → {x, y, z}, generally given by g(2) = x, g(3) = y, g(4) = z. Find g^-1 and prove that (g^-1)^-1 = g.

Answer:

The given function g : {2, 3, 4} → {x, y, z} which is given by g(2) = , g(3) = y, and g(4) = z

If we will define f: {x, y, z} → {2, 3, 4}, since f(x) = 2, f(y) = 3, f(z) = 4.

(gof)(x) = g(f(x)) = g(2) = x

(gof)(y) = g(f(y)) = g(3) = y

(gof)(z) = g(f(z)) = g(4) = z

And,

(fog)(2) = f(g(2)) = f(x) = 2

(fog)(3) = f(g(3)) = f(y) = 3

(fog)(4) = f(g(4)) = f(x) = 4

Thus,

fog = I_X and gof = I_Y, such that P = {2, 3, 4} and Q = {x, y, z}

Hence we know, the inverse of the function g exists and g^-1 = f

Thus,

g^-1 :{x, y, z} → {2, 3, 4} which is given by g^-1(x) = 2, g^-1(y) = 3 and g^-1(z) = 4

Let us now obtain the inverse for g^-1, i.e., finding the inverse of the function f.

Let us define h : {2, 3, 4} → {x, y, z} such that h(2) = x, h(3) = y and h(4) = z

In this case,

(foh)(2) = f(h(2)) = f(x) = 2

(foh)(3) = f(h(3)) = f(x) = 3

(foh)(4) = f(h(4)) = f(x) = 4

And,

(hof)(x) = h(f(x)) = h(2) = x

(hof)(y) = h(f(y)) = h(3) = y

(hof)(z) = h(f(z)) = h(4) = z

Hence we know, foh = I_X and hof = I_Y, P = {2, 3, 4} and Q = {x, y, z}.

So, the inverse of the function of f exists and f^-1 = h \(\boldsymbol{\Rightarrow }\) (g^-1)^-1 = h

We can see that, h = g

Hence we know, (f^-1)^-1 = f.

 

 

Q-12: Let us consider g : P → Q be an invertible function. Prove that the inverse of g^-1 is g, i.e., (g^-1)^-1 = g.

Answer:

We have,

g : P → Q is an invertible function.

Thus, there exists a function say, f : Q → P so that, fog = I_P and gof = I_Q

So, g^-1 = f

Then, fog = I_P and gof = I_Q

\(\boldsymbol{\Rightarrow }\) g^-1og= I_P and fof^-1 = I_Q

Therefore we have, g^-1 : Q → P will be invertible and the function g is the inverse of g^-1, i.e., (g^-1)^-1 = g

 

 

Q-13: If g : R → R is given by g(a) = \(\left (3 – a^{3} \right)^{\frac{1}{3}}\), then gog(a) is

(a) \(\frac{1}{a^{3}}\)

(b) a³

(c) a

(d) (3 – a³⁾

Answer:

g : R → R which is given by g(a) = \(\left (3 – a^{3} \right)^{\frac{1}{3}}\)

Then,

gog(a) = g(g(a)) = g\(\left (\left (3 – a^{3} \right)^{\frac{1}{3}} \right)\) = \(\left [3 – \left (\left (3 – a^{3} \right)^{\frac{1}{3}} \right)^{3} \right]^{\frac{1}{3}}\)

= \(\left [3 – \left (3 – a^{3} \right) \right]^{\frac{1}{3}}\) = \(\left (a^{3} \right)^{\frac{1}{3}} = a \)

Hence we know, gog(a) = a

Therefore we have, Answer is C.

 

 

Q-14: Let us consider a function g: R – \(\left \{-\frac{4}{3} \right \}\) → R as g(a) = \(\frac{4a}{3a + 4}\). The inverse of the function g is map f: Range g → R – \(\left \{-\frac{4}{3} \right \}\) is given by

(a) f(b) = \(\frac{3b}{3 – 4b}\) (b) f(b) = \(\frac{4b}{4 – 3b}\)

(c) f(b) = \(\frac{4b}{3 – 4b}\) (d) f(b) = \(\frac{3b}{4 – 3b}\)

Answer:

We have

g : R – \(\left \{-\frac{4}{3} \right \}\) → R which is a function defined as g(a) = \(\frac{4a}{3a + 4}\).

Assume, b be the arbitrary element having range g.

Thus, there exists a ɛ R – \(\left \{-\frac{4}{3} \right \}\) so that, b = f(a).

\(\boldsymbol{\Rightarrow }\) b = \(\frac{4a}{3a + 4}\)

\(\boldsymbol{\Rightarrow }\) b(3a + 4) = 4a

\(\boldsymbol{\Rightarrow }\) 3ab + 4b = 4a

\(\boldsymbol{\Rightarrow }\) a = \(\frac{4b}{4 – 3b}\)

Let, f : Range g → R – \(\left \{-\frac{4}{3} \right \}\) so that, f(b) = \(\frac{4b}{4 – 3b}\)

Thus,

fog(a) = f(g(a) = f\(\left (\frac{4a}{3a + 4} \right) = \frac{4\left (\frac{4a}{3a + 4} \right)}{4 – 3\left (\frac{4a}{3a + 4} \right)}\)

= \(\frac{16a}{12a + 16 – 12a} = \frac{16a}{16}\) = a

And,

gof(b) = g(f(b)) = g\(\left (\frac{4b}{4 – 3b} \right) = \frac{4\left (\frac{4b}{4 – 3b} \right)}{3\left (\frac{4b}{4 – 3b} \right) + 4}\)

= \(\frac{16b}{12b + 16 – 12b} = \frac{16b}{16} = b\)

Thus, fog = I_{R – \(\left \{- \frac{4}{3} \right \}\)} and gof = I_{Range f}

Therefore we have, the inverse of the function g is the map f: Range g → R – \(\left \{- \frac{4}{3} \right \}\), which will be given by

g(b) = \(\frac{4b}{4 – 3b}\)

Hence we know, Answer is b.

 

EXERCISE – 1.4

Q-1: Check whether each of the following definitions gives a binary operation or not.

In each of the event, that * will not be a binary operation, give explanation for this condition.

(i) On Z⁺, define * by x * y = x – y

(ii) On Z⁺, define * by x * y = xy

(iii) On R, define * by x * y = xy²

(iv) On Z⁺, define * by x * y = |x – y|

(v) On Z ⁺, define * by x * y = x

 

Answer:

(i) On Z⁺, * will be defined by x * y = x – y

It’s not a binary operation,

Such that the image of (2, 3) under * is 2 * 3 = 2 – 3 = -1 \(\notin \; Z^{+}\)

 

(ii) On Z⁺, * will be defined by x * y = xy.

So for every x, y ɛ \(\; Z^{+}\), there will be a unique element xy in Z⁺ .

It implies that '*' carries every pair (x, y) from the unique element x * y = xy in Z⁺.

Hence we know, '*' is the binary operation.

 

(iii) On R, * will be defined as x * y = xy².

We can see that for every x, y ɛ R, there will be a unique element xy² in R.

It implies that * will carry each pair (x, y) to a unique element x * y = xy² in R.

Hence we know, * is a binary operation.

 

(iv) On Z⁺, * will be defined as x * y =|x – y|.

We can see that for every x, y ɛ Z⁺, there will be a unique element |x – y| in Z⁺.

It means that '*' will carry each pair (x, y) to a unique element x * y = |x – y| in Z⁺.

Hence we know, '*' is a binary operation.

 

(v) On Z⁺, * will be defined as x * y = x.

We can see that for every x, y ɛ Z⁺, there will be a unique element x in Z⁺.

It means that * will carry each pair (x, y) to a unique element x * y = x in Z⁺.

Hence we know, * is a binary operation.

 

 

Q-2: For every binary operations * which is defined below, check whether * is associative or commutative in the following cases.

(i) On Z, explain x * y = x – y

(ii) On Q, explain x * y = xy + 1

(iii) On Q, explain x * y = \(\frac{xy}{2}\)

(iv) On Z⁺, explain x * y = 2^xy

(v) On Z⁺, explain x * y = x^y

(vi) On R – {-1}, explain x * y = \(\frac{x}{y + 1}\)

Answer:

(i) On Z, * will be defined as x * y = x – y

(2 * 3) * 4 = (2 – 3)* 4 = -1 * 4 = -1 – 4 = -5

2*(3 * 4) = 2 *(3 – 4) = 2 * -1 = 2 – (-1) = 3

Thus,

(2 * 3) * 4 ≠ 2*(3 * 4), where 2, 3, 4 ɛ Z.

Therefore we have, the given operation * is not associative.

We have 2 * 3 = 2 – 3 = -1 and 3 * 2 = 3 – 2 = 1

Since, 2 * 3 ≠ 3 * 2, where 2, 3 ɛ Z

Therefore we have, the given operation * is not associative.

(ii) On Q, * will be defined as x * y = xy + 1

We can observe here that,

(2 * 3)* 4 = (2 × 3 + 1) * 3 = 7 * 3 = 7 × 3 + 1 = 22

2 *(3 * 4) = 2 * (3 × 4 + 1) = 2 * 13 = 2 × 13 + 1 = 27

Thus,

(2 * 3)* 4 ≠ 2 *(3 * 4), where 2, 3, 4 ɛ Q.

Therefore we have, the given operation * is not associative.

In this case, also

We know that: xy = ya for every x, y ɛ Q.

\(\boldsymbol{\Rightarrow }\) xy + 1 = yx + 1 for every x, y ɛ Q

\(\boldsymbol{\Rightarrow }\) x * y = x * y for every x, y ɛ Q

Therefore we have, the given operation * is commutative.

 

(iii) On Q, * will be defined by x * y = \(\frac{xy}{2}\)

For every x, y, z ɛ Q, we have

(x * y)* z = \(\left (\frac{xy}{2} \right) * z = \frac{\left (\frac{xy}{2} \right)z}{2} = \frac{xyz}{4}\)

And,

x *(y * z) = \( x * \left (\frac{yz}{2} \right) = \frac{x \left (\frac{yz}{2} \right)}{2} = \frac{xyz}{4}\)

Thus,

(x * y)* z = x *(y * z), where x, y, z ɛ Q

Hence we know, the given operation * is associative.

We know that, xy = yx for every x, y ɛ Q

\(\boldsymbol{\Rightarrow }\) \(\frac{xy}{2} = \frac{yx}{2}\) for every x, y ɛ Q.

\(\boldsymbol{\Rightarrow }\) x * y = y * x for every x, y ɛ Q.

Hence we know, the given operation * is commutative.

 

(iv) On Z⁺, * will be defined by x * y = 2^xy

For every x, y, z ɛ Q, we have

(1 * 3)* 4 = 2^{1 × 3} * 4 = 8 * 4 = 2^{8 × 4}

And,

1 *(3 * 4) = 1 * 2^{3 × 4} = 1 * 4096 = 2^{1 × 4096}

Thus,

(1 * 3)* 4 ≠ 1 *(3 * 4), where x, y, z ɛ Q

Hence we know, the given operation * is not associative.

We know , xy = yx for every x, y ɛ Q

\(\boldsymbol{\Rightarrow }\) 2^xy = 2^yx for every x, y ɛ Q.

\(\boldsymbol{\Rightarrow }\) x * y = y * x for every x, y ɛ Q.

Hence we know, * is commutative in this case.

 

(v) On Z⁺, * will be defined by x * y = x^y

We can see that,

For every x, y, z ɛ Z⁺, we have

(1 * 3)* 4 = 1³ * 4 = 1 * 4 = 1 ⁴ = 1

And,

1 *(3 * 4) = 1 * 3 ⁴ = 1 * 81 = 1⁸¹ = 1

Thus,

(1 * 3)* 4 = 1 *(3 * 4), where x, y, z ɛ Z⁺

Hence we know, * is associative.

We have also got,

2 * 3 = 2³ = 8 and 3 * 2 = 3² = 9

Hence we know, 2 * 3 ≠ 3 * 2, where x, y, z ɛ Z⁺

Therefore we have, * is not commutative here.

 

(vi) On R, * – {-1} which is defined as x * y = \(\frac{x}{y + 1}\)

We can see that

(2 * 3)* 4 = \(\left (\frac{2}{3 + 1} \right) * 4 = \left (\frac{2}{4} \right) * 4 = \frac{\frac{1}{2}}{4 + 1} = \frac{1}{2 \times 4} = \frac{1}{8}\)

And,

2 *(3 * 4) = \(2 * \left (\frac{3}{4 + 1} \right) = 2 * \left (\frac{3}{5} \right) = \frac{2}{\frac{3}{5} + 1} = \frac{1}{\frac{3 + 5}{5}} = \frac{5}{8}\)

Thus,

(2 * 3)* 4 ≠ 2 *(3 * 4), where 2, 3, 4 ɛ R – {-1}

Hence we know, here the operation * is not associative.

 

 

Q-3: Let us consider a binary operation ^ for the set {2, 3, 4, 5, 6} which will be defined as x ^ y = min {x, y}.

Draw the operational table for the operation ^.

Answer:

As per the data given in the question, we have

A binary operation ^ for the set {2, 3, 4, 5, 6} which will be defined as x ^ y = min {x, y}.

Then,

x, y ɛ {2, 3, 4, 5, 6}

Hence we know, the operational table for the operation ^ given in the question will be :

^	2	3	4	5	6
2	2	2	2	2	2
3	2	3	3	3	3
4	2	3	4	4	4
5	2	3	4	5	5
6	2	3	4	5	6

 

Q-4: Let us consider a binary operation * for the set {2, 3, 4, 5, 6} which is given by the multiplication table given below:

(i) Find the value of (3 * 4) * 5 and 3 *(4 * 5).

(ii) Check whether * is commutative.

(iii) Find the value of (3 * 4)*(5 * 6)

*	2	3	4	5	6
2	2	2	2	2	2
3	2	3	2	2	3
4	2	2	4	2	2
5	2	2	2	5	5
6	2	3	2	5	6

 

Answer:

(i) (3 * 4)* 5 = 2 * 5 = 2

3 *(4 * 5) = 3 * 2 = 2

(ii) For each x, y ɛ {2, 3, 4, 5, 6}, we have x * y = y * x

Hence we know, the operation is commutative.

(iii) (3 * 4)*(5 * 6) = 2 * 5 = 2

Q-5: Let us consider *’ be a binary operation for the set {2, 3, 4, 5, 6} which will be defined by x *’ y = HCF of x * y. Now we check whether the operation *’ is the same as the operation * which is defined and used previously? Also, do justify your answer.

Answer:

A binary operation for the set {2, 3, 4, 5, 6} which will be defined by x * y = HCF of x and y.

The operational table for the operation *’ is given as the table below:

*’	2	3	4	5	6
2	2	2	2	2	2
3	2	3	2	2	3
4	2	2	4	2	2
5	2	2	2	5	5
6	2	3	2	5	6

 

Here, the operational table for the operation * and *’ is the same.

Hence we know, the operation *’ is the same as * operation.

 

 

Q-6: Let us consider a binary operation * on N which is given by x * y = LCM of x and y. Find the following:

(i) 6 * 7, 21 * 18 (ii) Is the operation * commutative?

(iii) Is the operation * associative? (iv) Obtain the identity of * in N.

(v) Which of the element of N are invertible for the operation *?

Answer:

As per the data given in the question, we have

A binary operation * on N which is given by x * y = LCM of x and y.

(i) 6 * 7 = LCM of 6 and 7 = 42

21 * 18 = LCM of 21 and 18 = 126

 

(ii) We know that from given data,

LCM of x and y = LCM of y and x for every x, y ɛ N.

Hence we know, x * y = y * x

Therefore we have, the given operation * is commutative.

(iii) For x, y, z ɛ N, we have

(x * y) * z = (LCM of x and y) * z = LCM of x, y and z

x * (y * z) = x * (LCM of y and z) = LCM of x, y and z

Hence we know,

(x * y) * z = x * (y * z)

Therefore we have, the given operation * is associative.

 

(iv) We know that:

LCM of x and 1 = LCM of 1 and x = x for all x ɛ N

\(\boldsymbol{\Rightarrow }\) x * 1 = x = 1 * x for all x ɛ N

Therefore we have, 1 is an identity of * in N.

 

(v) The element x in N will be invertible with respect to the operation *, if there will exist an element y in N, so that x * y = e = y * x

Here, e = 1

This means,

LCM of x and y = 1 = LCM of y and x

This case will only be possible when x and y is equal to 1.

Therefore we have, 1 is the only element which is invertible to N with respect to the operation *

 

 

Q-7: Check whether the operation * is defined for the set {1, 2, 3, 4, 5} by x * y = LCM of x and y, is a binary operation? Also, do justify your answer.

Answer:

The operation * for the set R = {1, 2, 3, 4, 5} which is defines as x * y = LCM of x and y.

Thus,

The operational table for the given operation * will be given by:

*	1	2	3	4	5
1	1	2	3	4	5
2	2	4	6	8	10
3	3	6	9	12	15
4	4	8	12	16	20
5	5	10	15	20	25

 

We can observe from the table defined above that,

2 * 3 = 3 * 2 = 6 \(\notin \) R,

2 * 5 = 5 * 2 = 10 \(\notin \) R,

3 * 4 = 4 * 3 = 12 \(\notin \) R,

3 * 5 = 5 * 3 = 15 \(\notin \) R,

4 * 5 = 5 * 4 = 20 \(\notin \) R

Therefore we have, the operation * is not a binary operation.

Q- 8: Let us consider a binary operation * on N which is defined by x * y = HCF of x and y. Check whether * is commutative? Check whether * is associative? Check whether there exists any identity for the binary operation * on N?

Answer:

A binary operation * on N which is defined by x * y = HCF of x and y

We know that,

HCF of x and y = HCF of y and x for every x, y ɛ N

Thus,

x * y = y * x

Hence we know, the binary operation * is commutative.

For x, y, z \(\epsilon \), we have

(x * y)* z = (HCF of x and y)* z = HCF of x, y and z

x *(y * z) = x *(HCF of y and z) = HCF of x, y and z.

Hence we know, (x * y)* z = x *(y * z)

Thus, the binary operation * is associative.

Then,

An element e ɛ N is the identity for the binary operation * if, x * e = x = e * x for every x ɛ N.

This is false for any x ɛ N.

Therefore we have, the given binary operation * don’t have any identity in N.

 

 

Q-9: Let us consider a binary operation * for the set Q of the rational numbers for the following:

(i) x * y = x – y (ii) x * y = x² + y²

(iii) x * y = x + xy (iv) x * y = (x – y)²

(v) x * y = \(\frac{xy}{4}\) (vi) x * y = xy²

Determine which of the binary operations are commutative and which are associative.

Answer:

(i) On Q, the binary operation * is defined by x * y = x – y. It will be observed that:

\(\frac{1}{3} * \frac{1}{4} = \frac{1}{3} – \frac{1}{4} = \frac{4 – 3}{12} = \frac{1}{12}\)

And,

\(\frac{1}{4} * \frac{1}{3} = \frac{1}{4} – \frac{1}{3} = \frac{3 – 4}{12} = -\frac{1}{12}\)

Therefore we have, \(\frac{1}{3} * \frac{1}{4} \neq \frac{1}{4} * \frac{1}{3}\), where, \(\frac{1}{3}, \; \frac{1}{4}\) ɛ Q.

Hence we know, the binary operation * is not commutative.

It will be observed that,

\(\left (\frac{1}{3} * \frac{1}{4} \right) * \frac{1}{5} = \left (\frac{1}{3} – \frac{1}{4} \right) * \frac{1}{5} = \left (\frac{4 – 3}{12} \right) * \frac{1}{5} = \frac{1}{12} * \frac{1}{5} = \frac{1}{12} – \frac{1}{5} = \frac{5 – 12}{60} = \frac{-7}{60}\)

And,

\(\frac{1}{3} * \left (\frac{1}{4} * \frac{1}{5} \right) = \frac{1}{3} * \left (\frac{1}{4} – \frac{1}{5} \right) = \frac{1}{3} * \left (\frac{5 – 4}{20} \right) = \frac{1}{3} * \frac{1}{20} = \frac{20 – 3}{60} = \frac{17}{20}\)

Thus,

\(\left (\frac{1}{3} * \frac{1}{4} \right) * \frac{1}{5} = \frac{1}{3} * \left (\frac{1}{4} * \frac{1}{5} \right)\), where \(\frac{1}{3}, \frac{1}{4} \; and \; \frac{1}{4} \; \epsilon \; Q\)

Therefore we have, the binary operation * is not associative.

 

(ii) On Q, the binary operation * is defined as x * y = x² + y².

For x, y ɛ Q, we have

x * y = x² + y² = y² + x² = y * x

\(\boldsymbol{\Rightarrow }\) x * y = y * x

Hence we know, the binary operation * is commutative.

We observe that,

(2 * 3)* 4 = (2² + 3²) * 4 = (4 + 9)* 4 = 13 * 4 = 13² + 4² = 185,

And,

2 * (3 * 4) = 2 * (3² + 4²) = 2 * (3 + 4) = 2 * 7 = 2² + 7² = 53

Thus, (2 * 3)* 4 ≠ 2 * (3 * 4), where 2, 3, 4 ɛ Q.

 

(iii) On Q, the binary operation * which is defined by x * y = x + xy

It will be observed that,

2 * 3 = 2 + 2 × 3 = 2 + 6 = 8

3 * 2 = 3 + 3 × 2 = 3 + 6 = 9

Thus, the binary operation * is not commutative.

It will be observed that,

(2 * 3)* 4 = (2 + 2 × 3)* 4 = (2 + 6)* 4 = 8 * 4 = 8 + 8 × 4 = 40

And,

2 * (3 * 4) = 2 * (3 + 3 × 4) = 2 * (3 + 12) = 2 * 15 = 2 + 2 × 15 = 32

Thus, (2 * 3)* 4 ≠ 2 * (3 * 4), where 2, 3, 4 ɛ Q.

Therefore we have, the binary operation * is not associative.

 

(iv) On Q, the binary operation * will be defined by x * y = (x – y)²

For x, y ɛ Q, we have

x * y = (x – y)²

y * x = (y – a)² = [-(x – y)]² = (x – y)²

Hence we know, the binary operation * is commutative.

We observe that,

(2 * 3)* 4 = (2 – 3)² * 4 = 1 * 4 = (1 – 4)² = (-3)² = 9

And,

2 * (3 * 4) = 2 * (3 – 4)² = 2 * 1 = (2 – 1)² = (-1)² = 1

Thus, (2 * 3)* 4 ≠ 2 * (3 * 4), where 2, 3, 4 ɛ Q.

Therefore we have, the binary operation * is not associative.

 

(v) On Q, the binary operation * will be defined as x * y = \(\frac{xy}{4}\)

For x, y ɛ Q, we will get

x * y = \(\frac{xy}{4}\) = \(\frac{yx}{4}\) = y * x

Hence we know, x * y = y * x

Therefore we have, the binary operation * is commutative.

For x, y, z \(\epsilon \)Q, we will get

(x * y) * z = \( \left (\frac{xy}{4} \right) * z = \frac{\left (\frac{xy}{4} \right). z}{4} = \frac{xyz}{16}\)

And,

x * (y * z) = \( x * \left (\frac{yz}{4} \right) = \frac{x * \left (\frac{yz}{4} \right)}{4} = \frac{xyz}{16}\)

Hence we know, (x * y) * z = x * (y * z), where x, y, z \(\epsilon \)

Therefore we have, the binary operation * is associative.

(vi) On Q, the binary operation * will be defined as x * y = xy².

We can observe that,

\(\frac{1}{3} * \frac{1}{4} = \frac{1}{3}.\left (\frac{1}{4} \right)^{2} = \frac{1}{3} . \frac{1}{16} = \frac{1}{48}\)

And,

\(\frac{1}{4} * \frac{1}{3} = \frac{1}{4}.\left (\frac{1}{3} \right)^{2} = \frac{1}{4} . \frac{1}{9} = \frac{1}{36}\)

Hence we know, \(\frac{1}{3} * \frac{1}{4}\) ≠ \(\frac{1}{4} * \frac{1}{3}\), where \(\frac{1}{3} \; and \; \frac{1}{4} \) ɛ Q.

Therefore we have, the binary operation * is not commutative.

We can also observe that:

\(\left (\frac{1}{3} * \frac{1}{4} \right) * \frac{1}{5} = \left [\frac{1}{3}\left (\frac{1}{4} \right)^{2} \right] * \frac{1}{5} = \frac{1}{48} * \frac{1}{5} = \frac{1}{48} * \left (\frac{1}{5} \right)^{2} = \frac{1}{48 \times 25} = \frac{1}{1200}\)

And,

\(\frac{1}{3} * \left (\frac{1}{4} * \frac{1}{5} \right) = \frac{1}{3}\left [\frac{1}{4}\left (\frac{1}{5} \right)^{2} \right] = \frac{1}{3} * \frac{1}{100} = \frac{1}{3} * \left (\frac{1}{100} \right)^{2} = \frac{1}{3 \times 10000} = \frac{1}{30000}\)

Hence we know, \(\left (\frac{1}{3} * \frac{1}{4} \right) * \frac{1}{5} ≠ \frac{1}{3} * \left (\frac{1}{4} * \frac{1}{5} \right)\), where \(\frac{1}{3}, \frac{1}{4}, \frac{1}{5} \; \epsilon \; Q \)

Therefore we have, the binary operation * is not associative.

Thus, the operations which are defined in (ii), (iv), (v) are commutative and the operation defined in (v) is only associative.

Q-10: Check the identity of the operations which are equated above.

 

Answer:

Consider an element e ɛ Q which can be the identity element for the operation * if,

x * e = x = e * x, for every x ɛ Q.

Here, in each of the six operations, there is no element e ɛ Q, which satisfies the above condition.

Hence we know, none of the six operations in above case have identity.

 

 

Q-11: Let us consider M = N × N and * be the binary operation on M which can be defined by

(p, q)* (r, s) = (p + r, q + s).

Prove that the operation * is commutative and associative. If there is any possibility of having an identity element, then what will be the identity element for the operation * on M?

 

Answer:

M = N × N and * be the binary operation on M which can be defined by

(p, q)* (r, s) = (p + r, q + s)

Let, (p, q), (r, s) ɛ M

Then,

p, q, r, s ɛ N

Here, we have

(p, q)*(r, s) = (p + r, q + s)

(r, s)*(p, q) = (r + p, s + q) = (p + r, q + s)

[Addition is commutative on the set of the natural numbers]

Thus, (p, q)*(r, s) = (r, s)*(p, q)

Hence we know, the operation * is commutative here.

Let, (p, q), (r, s), (t, u) ɛ M

Then, p, q, r, s, t, u ɛ N

In this case,

[(p, q)*(r, s)] * (t, u) = (p + r, q + s)*(t, u) = (p + r + t, q + s + u)

And,

(p, q) * [(r, s) * (t, u)] = (p, q)*(r + t, s + u) = (p + r + t, q + s + u)

Thus, [(p, q)*(r, s)] * (t, u) = (p, q) * [(r, s) * (t, u)]

Hence we know, the operation * is associative.

Consider an element e = (e₁, e₂) ɛ M which can be an identity element for * operation, if

x * e = x = e * x, for every x = (x₁, x₂) ɛ M

Then,

(x₁ + e₁, x₂ + e₂) = (x₁, x₂) = (e₁ + x₁, e₂ + x₂),

This cannot be true for every element in M.

Hence we know, the operation * will not have any identity element.

 

 

Q-12: Check whether the statements given below are true or false. Also, justify your answer.

(i) For any arbitrary binary operation * for the set N, x * x = x for every x ɛ N.

(ii) If the operation * is a commutative binary operation for N, then x *(y * z) = (z * y)* x.

Answer:

(i) Explain a binary operation * on N as x * y = x + y for every x ɛ N.

Thus, for y = x = 4, we have

4 * 4 = 4 + 4 = 8 ≠ 3.

Hence we know, the statement (i) is false.

(ii) RHS = (z * y)* x

= (y * z)* x [* is commutative]

= x * (y * z) [Again, as * is commutative]

= LHS

Therefore we have, x *(y * z) = (z * y)* x

Hence we know, statement (ii) is true.

 

 

Q-13: Let us consider a binary operation * for N defined as x * y = x³ + y³. Select the correct answer.

(a) Is * commutative but, not associative?

(b) Is * both commutative and associative?

(c) Is * neither commutative nor associative?

(d) Is * associative but, not commutative?

Answer:

On N, the binary operation * will be defined as x * y = x³ + y³.

For x, y ɛ N, we have

x * y = x³ + y³ = y³ + x³ = y * x [Addition is commutative in N]

Hence we know, the binary operation * is commutative in this case.

We can observe that,

(2 * 3)* 4 = (2³ + 3³)* 4 = (8 + 27)* 4 = 35 * 4 = 35³ + 4⁴ = 42875 + 16 = 42891

And,

2 *(3 * 4) = 2 *(3³ + 4³) = 2 *(27 + 64) = 2 * 91 = 2³ + 91³ = 8 + 753571 = 753579

(2 * 3)* 4 ≠ 2 *(3 * 4), where 2, 3, 4 ɛ N

Thus, the operation * is not associative in this case.

Therefore we have, the operation * is commutative but, not associative in this case.

Hence we know, Answer is a.

Previous

Next